5.4中心对称

(共15张PPT)
中心对称
5.4 中心对称
绍兴县实验中学 唐秀萍
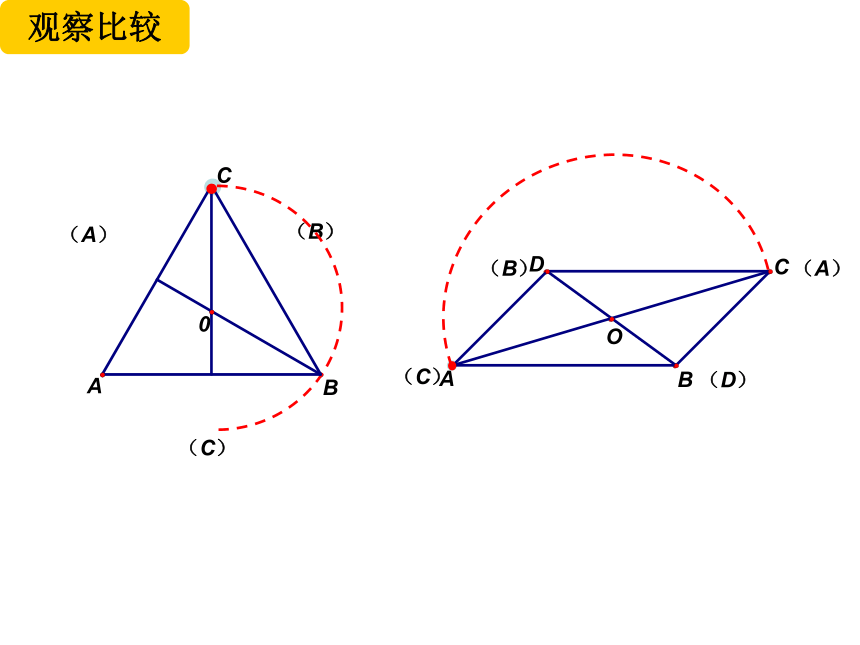
观察比较
（A）
（B）
（C）
（A）
（C）
（B）
（D）
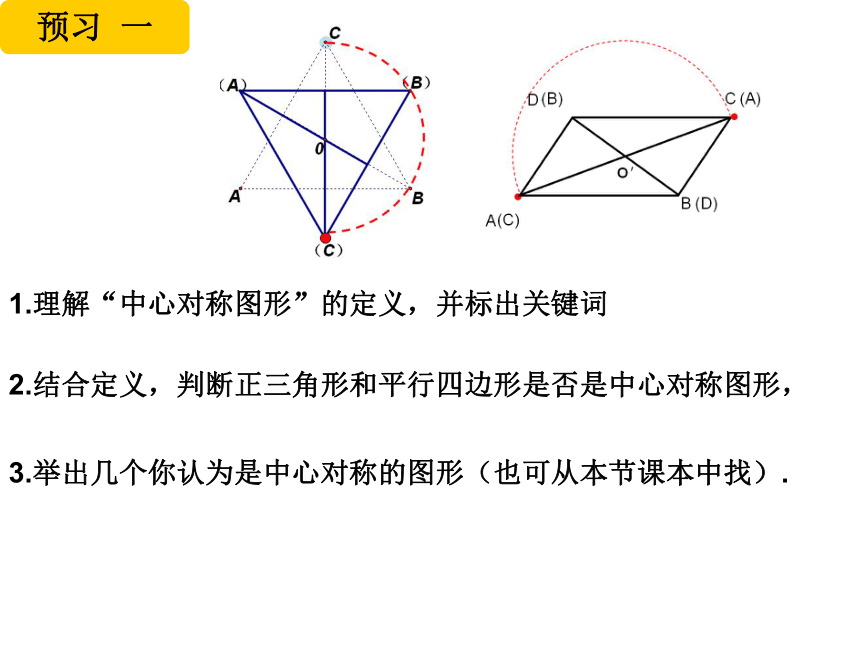
预习 一
1.理解“中心对称图形”的定义，并标出关键词
2.结合定义，判断正三角形和平行四边形是否是中心对称图形，
3.举出几个你认为是中心对称的图形（也可从本节课本中找）.
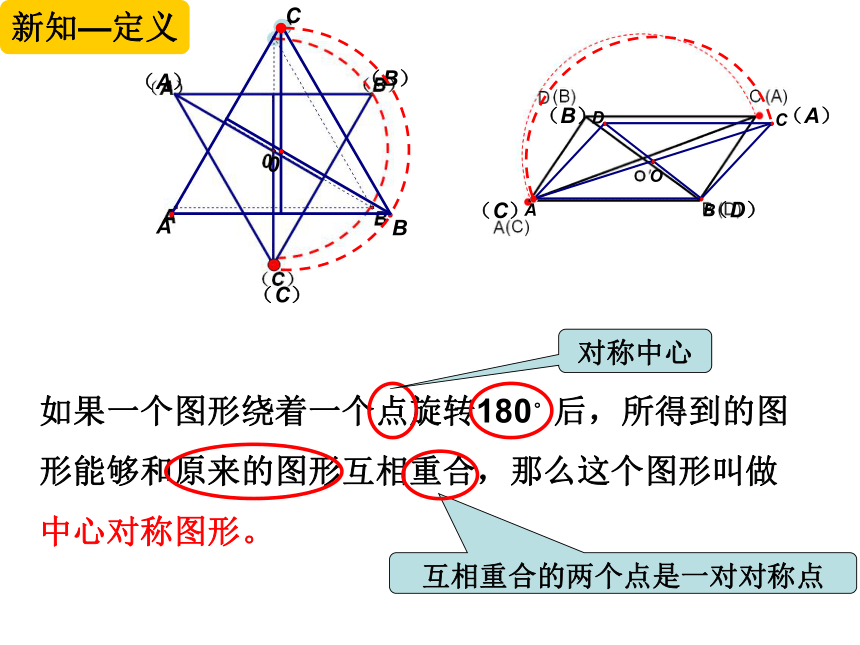
新知—定义
（A）
（C）
（B）
（D）
如果一个图形绕着一个点旋转180。后，所得到的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形。
对称中心
互相重合的两个点是一对对称点
（A）
（B）
（C）
A
O
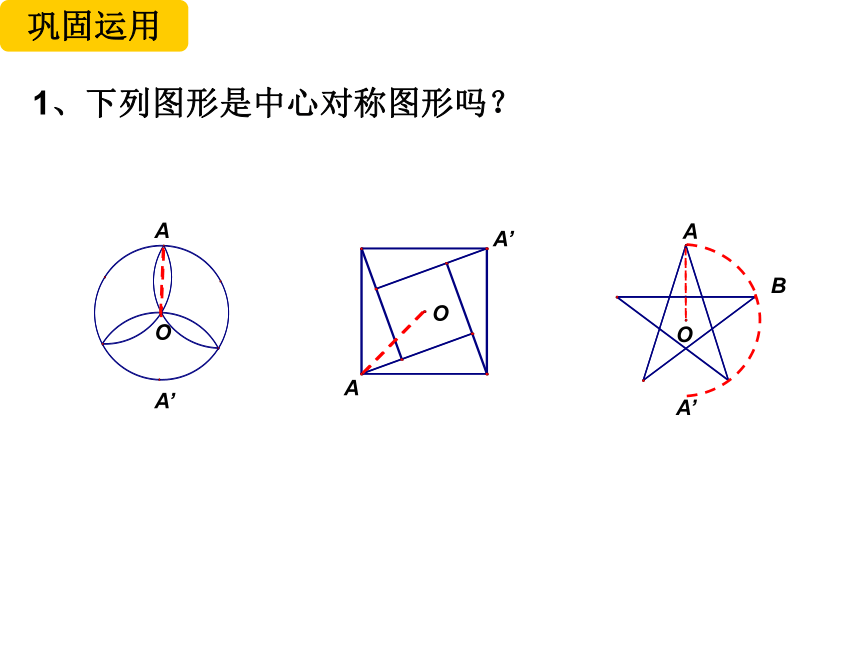
巩固运用
A
A’
O
O
A
1、下列图形是中心对称图形吗？
A’
A’
B
O
A
B
C
E
F
D
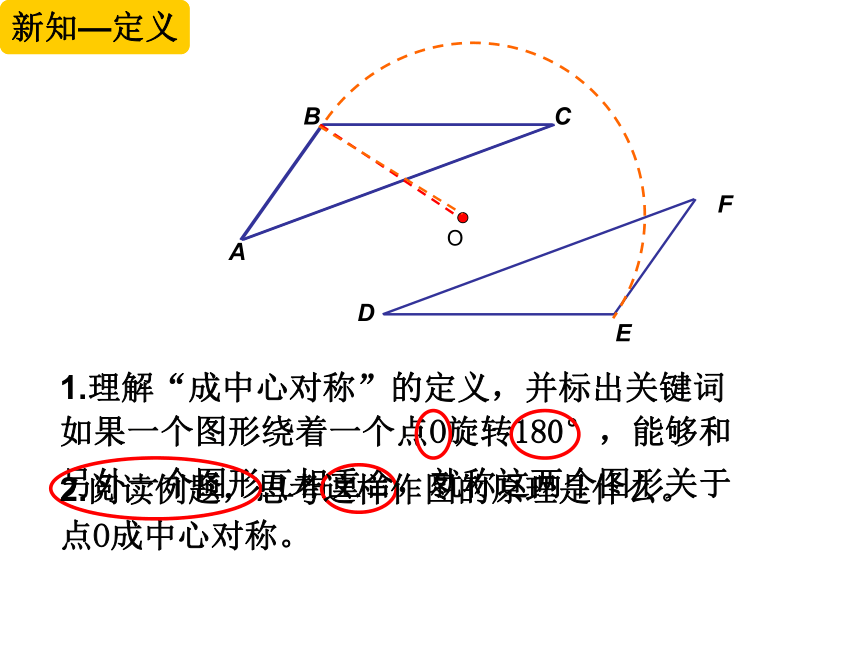
1.理解“成中心对称”的定义，并标出关键词
如果一个图形绕着一个点O旋转180°，能够和另外一个图形互相重合，就称这两个图形关于点O成中心对称。
2.阅读例题，思考这样作图的原理是什么。
预习 二
新知—定义
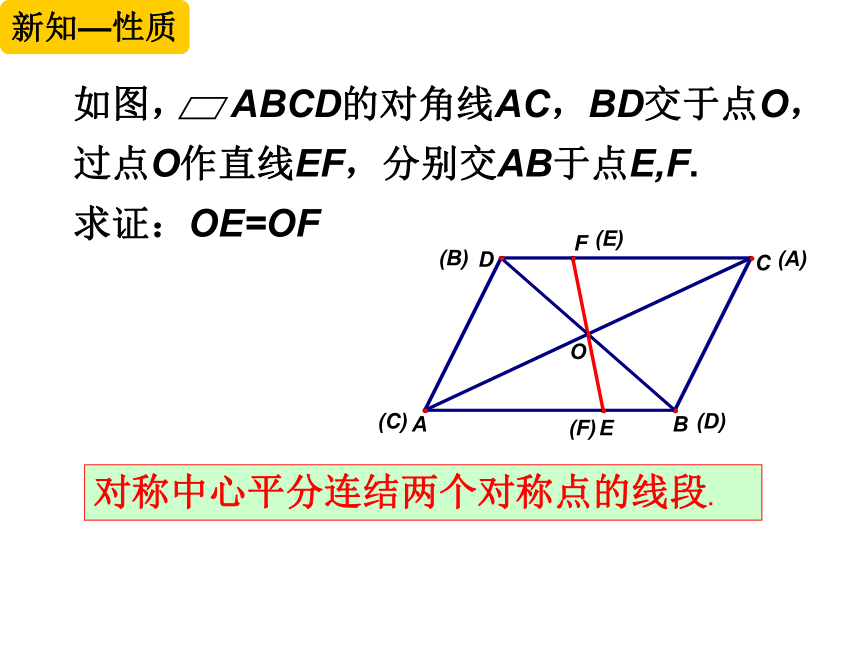
对称中心平分连结两个对称点的线段.
新知—性质
如图， ABCD的对角线AC，BD交于点O，过点O作直线EF，分别交AB于点E,F.
求证：OE=OF
(A)
(C)
(B)
(D)
(F)
(E)
例、如图，已知△ABC 和点O,作△A’B’C’，使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
对称中心平分连结两个对称点的线段.
变式1：已知△ABC和点O，作△A'B'C'，使△A'B'C'与△ABC关于点O成中心对称。
新知—应用
变式2：已知△ABC和点O，作△A'B'C'，使△A'B'C'与△ABC关于点O成中心对称。
B
A
C
O
B
A
C
O
回顾总结
本节课你学习了那些新知识……
作一个图形，使得它与原图形关于某个点成中心对称
两个定义：
中心对称图形
成中心对称
对称中心平分连结两个对称点的线段
一条性质：
一种作图方法：
轴对称图形 成轴对称
是一个图形
是一种图形变换，
包含两个图形
都有对称轴，翻折后都会重合
如果把关于某条直线成轴对称的两个图形看成一个整体，则这个整体为轴对称图形.
对比轴对称图形与成轴对称：
比较归纳
A
B
C
(B)
不同点
联系
A
B
C
A’
B’
C’
图形
相同点
中心对称图形 成中心对称
是一个图形
是一种图形变换，包含两个图形
都有旋转中心，旋转180°后都会重合
如果把关于某个点成中心对称的两个图形看成一个整体，则这个整体为中心对称图形.
对比中心对称图形与成中心对称：
类比归纳
图形
不同点
联系
相同点
如果一个图形绕着一个点旋转180。后，所得到的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形
如果一个图形绕着一个点O旋转180°，能够和另外一个图形互相重合，就称这两个图形关于点O成中心对称。
比较归纳
A
B
C
A’
B’
C’
轴 对 称
中 心 对 称
关于线对称
关于点对称
1.如图是五个小正方形拼成的图形.请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的新图形:
①是轴对称图形，但不是中心对称图形；
②是中心对称图形，但不是轴对称图形；
③既是轴对称图形,又是中心对称图形.
拓展提升
2、如图平行四边形ABCD，画一条直线将其面积二等分，你有多少种不同的方法？
变式：如图 ，如何用一条直线将其面积二等分？
拓展提升