浙教版初中数学八年级上册 2.4 等腰三角形的判定定理 课件(21张)
文档属性
| 名称 | 浙教版初中数学八年级上册 2.4 等腰三角形的判定定理 课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 13:34:09 | ||
图片预览


文档简介
(共21张PPT)
等腰三角形的判定
一、实践探究
提出问题
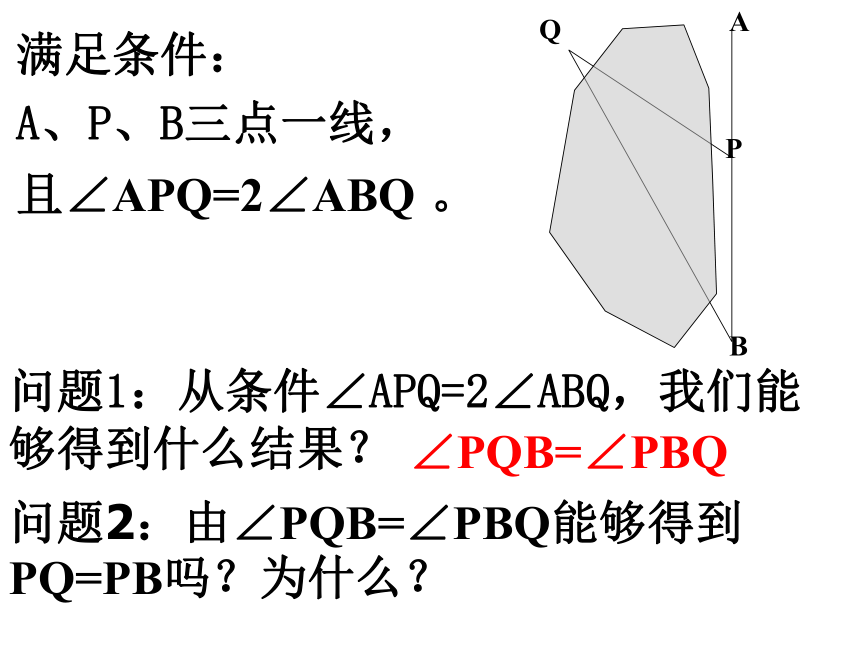
1.某班进行野外郊游,老师要求同学们测量P、Q两点间距离,但P、Q两点被一个水池隔开了,手上没有测量工具可以直接测量P、Q间距离。一位聪明的学生利用所学几何知识解决了这个问题。他从同学的书包内找到了两把圆规,当成简易“测角仪”,并先在水池的一侧空地上找了一个点A,连结AP并延长到B,使∠APQ=2∠ABQ,然后步量出BP的长度。这个长度就是PQ的距离。你认为这种方法正确吗?
满足条件:
A、P、B三点一线,
且∠APQ=2∠ABQ
。
A
B
P
Q
问题1:从条件∠APQ=2∠ABQ,我们能够得到什么结果?
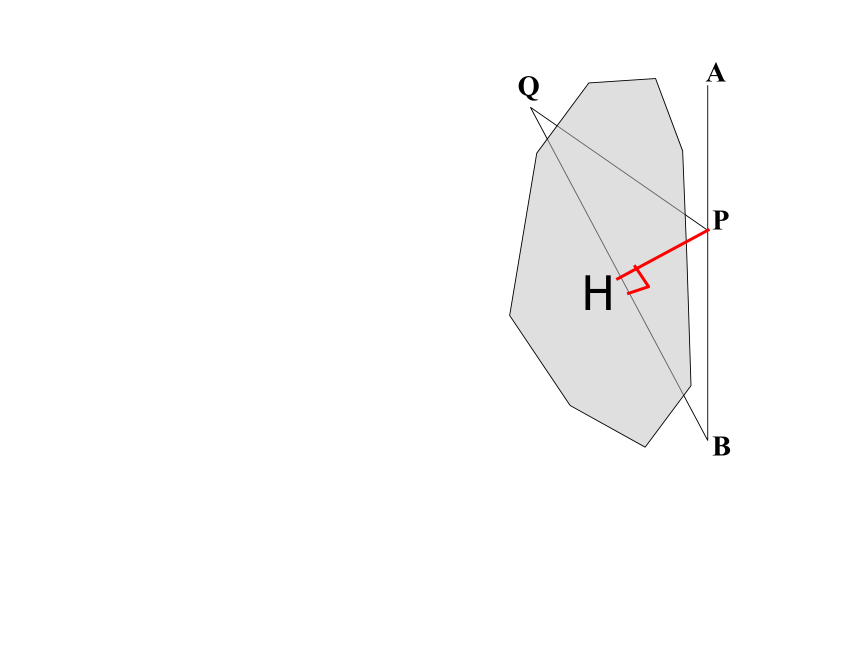
问题2:由∠PQB=∠PBQ能够得到PQ=PB吗?为什么?
∠PQB=∠PBQ
A
B
P
Q
H
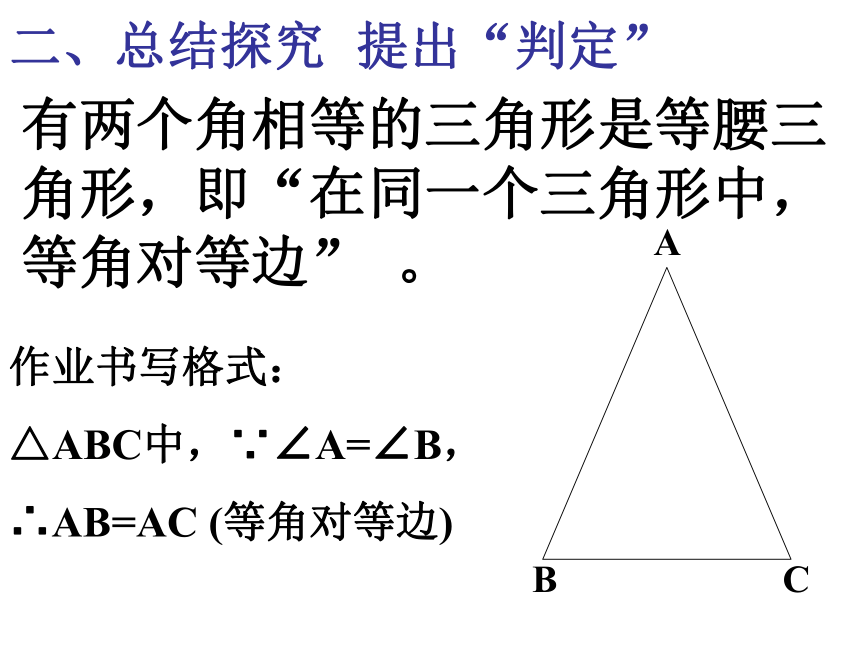
有两个角相等的三角形是等腰三角形,即“在同一个三角形中,等角对等边”
。
作业书写格式:
△ABC中,∵∠A=∠B,
∴AB=AC
(等角对等边)
二、总结探究
提出“判定”
A
C
B
三、举例分析
学会应用
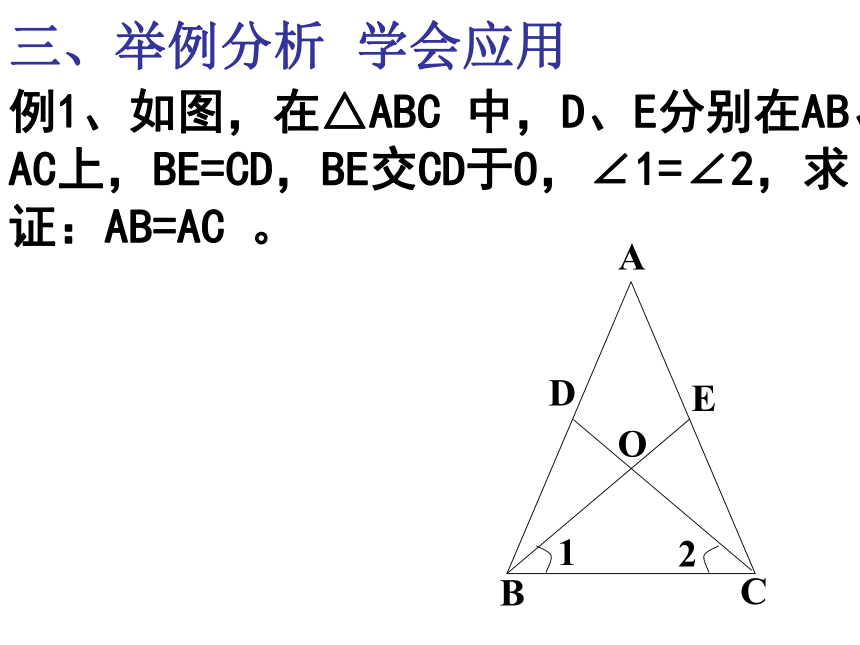
例1、如图,在△ABC
中,D、E分别在AB、AC上,BE=CD,BE交CD于O,∠1=∠2,求证:AB=AC
。
O
A
1
2
D
E
C
B
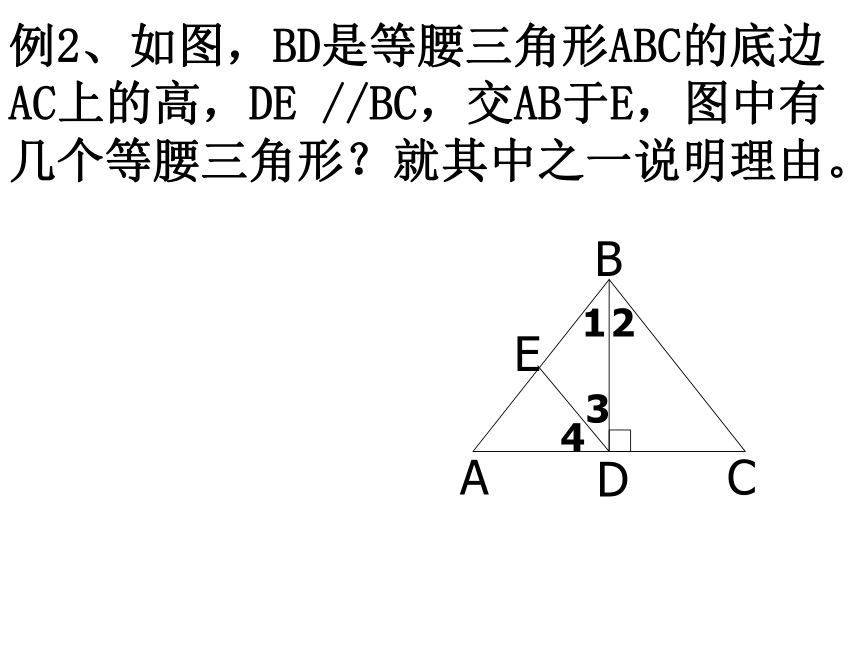
例2、如图,BD是等腰三角形ABC的底边AC上的高,DE
//BC,交AB于E,图中有几个等腰三角形?就其中之一说明理由。
A
B
C
D
E
1
2
3
4
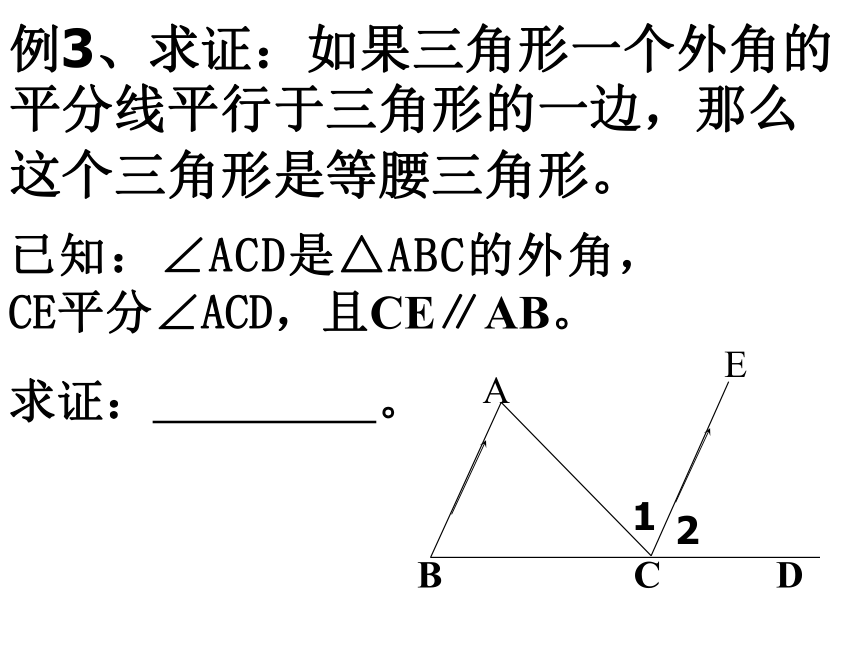
例3、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:∠ACD是△ABC的外角,CE平分∠ACD,且CE∥AB。
求证:
。
E
B
C
D
A
1
2
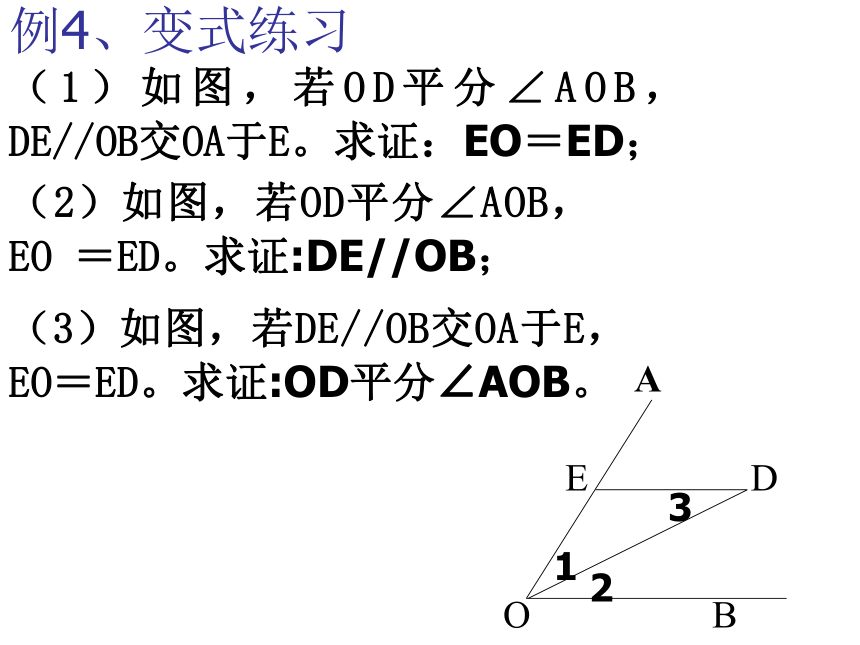
例4、变式练习
(1)如图,若OD平分∠AOB,DE//OB交OA于E。求证:EO=ED;
(2)如图,若OD平分∠AOB,EO
=ED。求证:DE//OB;
(3)如图,若DE//OB交OA于E,EO=ED。求证:OD平分∠AOB。
E
D
O
B
A
1
2
3
“角平分线、平行线、等腰三角形”这三者中,若有两条成立,则第三条必成立。熟悉这个结论,对解决包含该图形的较复杂的题目是很有帮助的。
总结:
四、同步练习
提高能力
练习1、如图,AD//BC,BD平分∠ABC。
求证:AB=AD。
B
C
A
D
1
2
3
练习2、(1)如图(a),AB=AC,BD平分∠ABC,CD平分∠ACB.图中有几个等腰三角形?
B
C
A
D
(a)
1
2
(2)如图(b),若过D作EF//BC交AB于E,交AC于F,图中有几个等腰三角形?
A
D
B
C
(b)
E
F
(3)如图(c),若将△ABC改为不等边三角形,其它条件不变,情况会如何?
A
D
B
C
(c)
E
F
(4)对于图(b)、(c)中,还可证出哪些线段的和差关系
A
D
B
C
(b)
E
F
A
D
B
C
(c)
E
F
(5)如图(d),若BD,CD分别平分∠ABC和∠ACB,过D作DE//AB交BC于E,作DF//AC交BC于F.求证:BC的长等于△DEF的周长。
A
B
C
D
E
F
五、课堂小结
反思过程
1.如何确定一个三角形是等腰三角形?
(1)用“全等法”证明两条边相等。
(2)用等腰三角形判定定理:有两个角相等的三角形是等腰三角形。
2.等腰三角形可用于证明线段相等、三线合一等。
等腰三角形基本图形认识
3.巩固练习
练习1.如图,△ABC中,BD平分∠ABC交AC于D,且AD=BD=BC,
问:图中有几个等腰三角形?请说明理由。
A
B
C
D
1
2
练习2.如图,OA平分∠BAC,∠1=∠2。
求证:AB=AC。
今天你们的表现非常出色!
等腰三角形的判定
一、实践探究
提出问题
1.某班进行野外郊游,老师要求同学们测量P、Q两点间距离,但P、Q两点被一个水池隔开了,手上没有测量工具可以直接测量P、Q间距离。一位聪明的学生利用所学几何知识解决了这个问题。他从同学的书包内找到了两把圆规,当成简易“测角仪”,并先在水池的一侧空地上找了一个点A,连结AP并延长到B,使∠APQ=2∠ABQ,然后步量出BP的长度。这个长度就是PQ的距离。你认为这种方法正确吗?
满足条件:
A、P、B三点一线,
且∠APQ=2∠ABQ
。
A
B
P
Q
问题1:从条件∠APQ=2∠ABQ,我们能够得到什么结果?
问题2:由∠PQB=∠PBQ能够得到PQ=PB吗?为什么?
∠PQB=∠PBQ
A
B
P
Q
H
有两个角相等的三角形是等腰三角形,即“在同一个三角形中,等角对等边”
。
作业书写格式:
△ABC中,∵∠A=∠B,
∴AB=AC
(等角对等边)
二、总结探究
提出“判定”
A
C
B
三、举例分析
学会应用
例1、如图,在△ABC
中,D、E分别在AB、AC上,BE=CD,BE交CD于O,∠1=∠2,求证:AB=AC
。
O
A
1
2
D
E
C
B
例2、如图,BD是等腰三角形ABC的底边AC上的高,DE
//BC,交AB于E,图中有几个等腰三角形?就其中之一说明理由。
A
B
C
D
E
1
2
3
4
例3、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:∠ACD是△ABC的外角,CE平分∠ACD,且CE∥AB。
求证:
。
E
B
C
D
A
1
2
例4、变式练习
(1)如图,若OD平分∠AOB,DE//OB交OA于E。求证:EO=ED;
(2)如图,若OD平分∠AOB,EO
=ED。求证:DE//OB;
(3)如图,若DE//OB交OA于E,EO=ED。求证:OD平分∠AOB。
E
D
O
B
A
1
2
3
“角平分线、平行线、等腰三角形”这三者中,若有两条成立,则第三条必成立。熟悉这个结论,对解决包含该图形的较复杂的题目是很有帮助的。
总结:
四、同步练习
提高能力
练习1、如图,AD//BC,BD平分∠ABC。
求证:AB=AD。
B
C
A
D
1
2
3
练习2、(1)如图(a),AB=AC,BD平分∠ABC,CD平分∠ACB.图中有几个等腰三角形?
B
C
A
D
(a)
1
2
(2)如图(b),若过D作EF//BC交AB于E,交AC于F,图中有几个等腰三角形?
A
D
B
C
(b)
E
F
(3)如图(c),若将△ABC改为不等边三角形,其它条件不变,情况会如何?
A
D
B
C
(c)
E
F
(4)对于图(b)、(c)中,还可证出哪些线段的和差关系
A
D
B
C
(b)
E
F
A
D
B
C
(c)
E
F
(5)如图(d),若BD,CD分别平分∠ABC和∠ACB,过D作DE//AB交BC于E,作DF//AC交BC于F.求证:BC的长等于△DEF的周长。
A
B
C
D
E
F
五、课堂小结
反思过程
1.如何确定一个三角形是等腰三角形?
(1)用“全等法”证明两条边相等。
(2)用等腰三角形判定定理:有两个角相等的三角形是等腰三角形。
2.等腰三角形可用于证明线段相等、三线合一等。
等腰三角形基本图形认识
3.巩固练习
练习1.如图,△ABC中,BD平分∠ABC交AC于D,且AD=BD=BC,
问:图中有几个等腰三角形?请说明理由。
A
B
C
D
1
2
练习2.如图,OA平分∠BAC,∠1=∠2。
求证:AB=AC。
今天你们的表现非常出色!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
