3.3.1圆心角

(共49张PPT)
义务教育课程标准实验教科　
浙江版《数学》九年级上册
执教者 夏羽晶
水杯的盖子为什么做成圆形？蕴含了圆的什么性质？
你可曾想过？
水是生命之源，水对于我们的身体，就好象氧气般重要！
O
C
D
A
B
E
2、由圆的轴对称性得到：
1、圆是 图形，
轴对称
直径所在的直线
每一条 都是它的对称轴。
垂径定理及逆定理
.
O
A
B
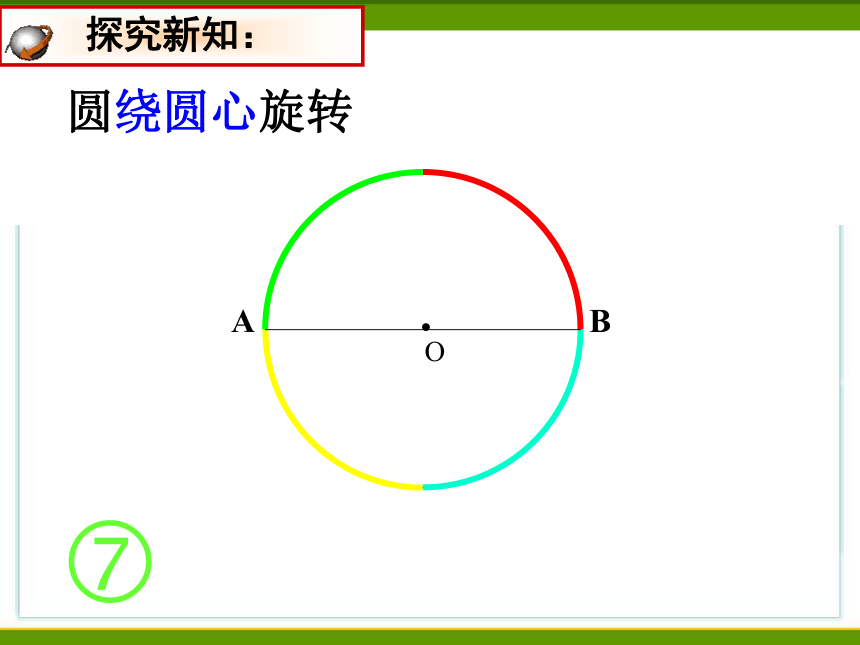
圆绕圆心旋转

探究新知：
.
O
A
B
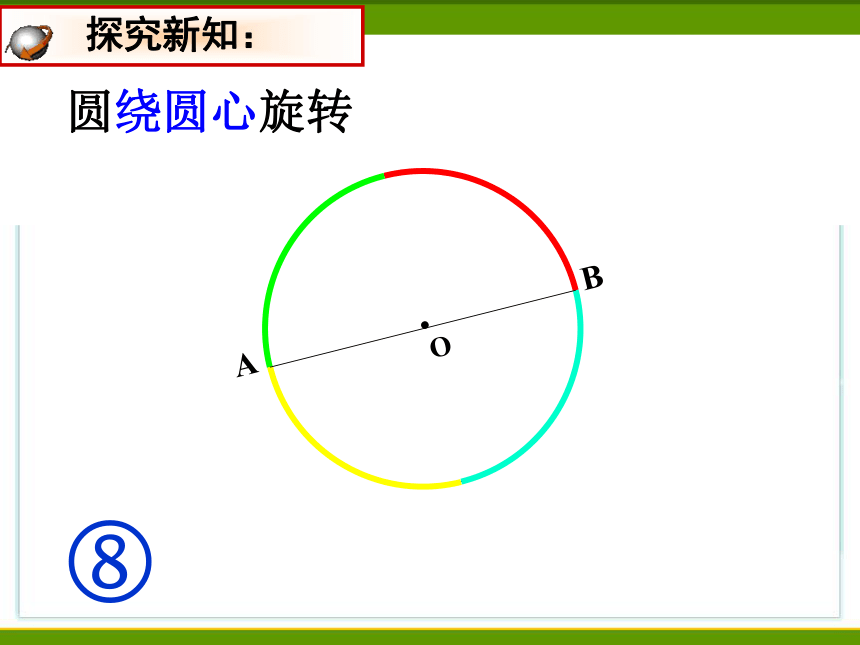
圆绕圆心旋转

探究新知：
.
O
A
B
圆绕圆心旋转

探究新知：
.
O
A
B
圆绕圆心旋转

探究新知：
.
O
B
A
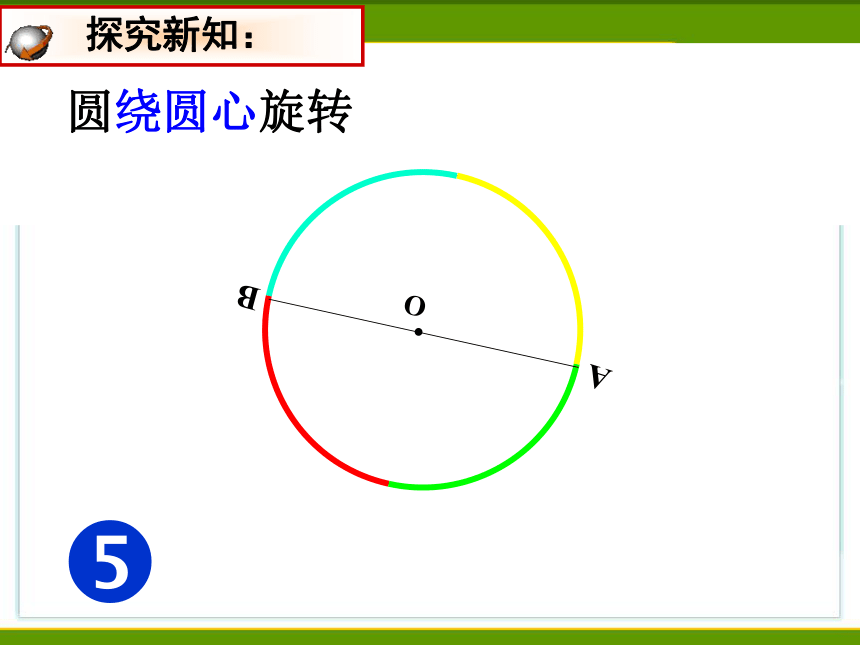
圆绕圆心旋转

探究新知：
.
O
B
A
圆绕圆心旋转

探究新知：
.
O
A
B
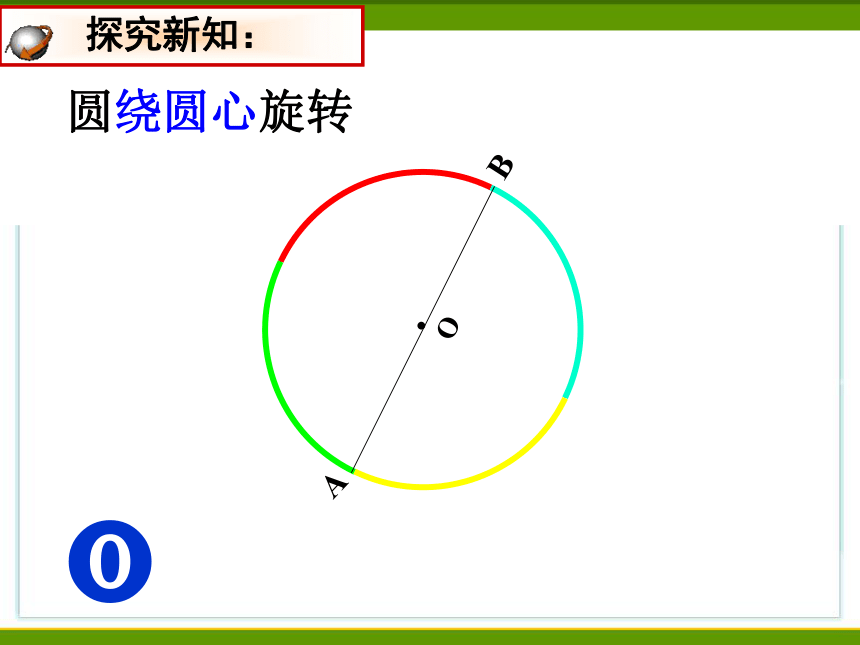
圆绕圆心旋转

探究新知：
.
O
B
A
180°
所以圆是中心对称图形，圆心是它的对称中心。
圆绕圆心旋转180°后,

仍与原来的圆重合。
得出结论：
N
O
把圆O的半径ON绕圆心O旋转任意一个角度 ，
继续探究：
N
O
N'
把圆O的半径ON绕圆心O旋转任意一个角度 ，
继续探究：
θ
N
O
N'
把圆O的半径ON绕圆心O旋转任意一个角度 ，
继续探究：
θ
N
O
N'
把圆绕圆心旋转任意一个角度后，
把圆O的半径ON绕圆心O旋转任意一个角度 ，
点N'
仍与原来的圆重合。
仍落在圆上。
得出结论：
θ
水杯的盖子为什么做成圆形？蕴含了圆的什么性质？
可见，数学与我们的生活是紧密相连的！
希望大家勤观察、多动脑，做学习和生活中的有心人！
解决疑问：
如图中所示， ∠ NO N '就是一个圆心角。
N
O
N'
形成概念：
顶点在圆心的角叫
圆心角
θ
义务教育课程标准实验教科　
浙江版《数学》九年级上册
判别下列各图中的角是不是圆心角，并说明理由。
①
②
③
④
及时反馈：
C
D
o
A
B
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
条件：
∠ AOB= ∠ COD
C
D
o
A
B
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
条件： AOB= COD
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
条件： AOB= COD
AB= CD，
⌒
⌒
AB=CD
猜想：
证明：
条件： AOB= COD
o
A
B
C
D
探索：在同一个圆中，两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
AB= CD，
⌒
⌒
AB=CD
猜想：
证明:
∵OA=OC ,OB=OD
∠AOB=∠COD,
∴把 ∠COD连同 CD、 弦CD 绕圆心O 旋转， 当点A与点C重合时，
点B与点D也重合。
∴　
AB= CD，
⌒
⌒
AB=CD
A
B
C
D
o
弦AB和弦ＣＤ对应的弦心距什么关系？
在同圆中，
Ｅ
Ｆ
∵ ∠ AOB= ∠ COD
∴AB=CD AB=CD
相等的圆心角所对的弧相等，　　　　　　　　
所对的弦相等，　　　　　　
所对弦的弦心距相等. 　　　
几何表述：
OE=OF
形成定理：
圆心角定理
如图，⊙O 和⊙O' 是等圆，
如果 ∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M'

对于等圆的情况 ， 命题成立。
因为两个等圆可叠合成同圆，所以等圆问题可转化为同圆问题.
同圆变等圆：
A
B
C
D
o
圆心角定理：　
在同圆或等圆中，
Ｅ
Ｆ
∵ ∠ AOB= ∠ COD
∴AB=CD
相等的圆心角所对的弧相等，　　　　　　　　
所对的弦相等，　　　　　　
所对弦的弦心距相等. 　　　
几何表述：
OE=OF
AB=CD
在同圆或等圆中，
相等的圆心角所对的弧相等，所对的弦也相等。
【注意】：
1.去掉“在同圆或等圆中”结论不一定成立。
2 .要证弧（弦）相等，只需证它们所对的圆心角相等。
分析定理：
圆心角定理
A
B
C
D
o
应用新知：
O
A
B
C
D
1
2
例 已知：如图,∠1=∠2.求证：AC=BD.
【变式】 已知：如图,∠1=∠2.
求证：AC=BD.
圆心角定理
圆心角相等
所对弧相等
所对弦相等
所对弦的弦心距相等
证明：∵ ∠ 1= ∠ 2
∴DC=BA（ ）
∴ DC+BC= BA+BC
即 BD=AC
反思：
圆心角定理
你能将⊙Ｏ二等分吗？　
Ｏ
作法:作⊙Ｏ的直径ＡＢ。
　　　　
　　　　　
　　　
Ａ　　　　　　Ｂ
　
　　　　
点A、B就把⊙Ｏ两等分。
再探新知：
用直尺和圆规你能把⊙Ｏ四等分吗？　
Ｏ
作法：
１、作⊙Ｏ的直径ＡＢ。
２、过点O作ＣＤ⊥ＡＢ，交⊙Ｏ于点Ｃ和 点 Ｄ。
点Ａ，Ｂ，Ｃ，Ｄ就把⊙Ｏ四等分
　　　　　
　　　Ｃ
　
　　　Ｄ　
你能将任意一个
圆六等分吗？
若要把圆作n等分，
关键是先作什么？
先n等分以圆心O为顶点的周角。
再探新知：
A B
则每一份的圆心角的度数是 。
因为相等的圆心角所对的弧 ，
所以每一份的圆心角所对的弧也 。
1
相等
相等
再探新知：
若按刚才这种方法把一个圆分成360份.
我们把1 的圆心角所对的弧叫做1 的弧.
定义：弧的度数
80°的弧
80°
概括新知：
1 的圆心角所对的弧叫做1 的弧.
性质：弧的度数和它所对圆心角的度数相等。
弧的度数：
写法：若∠COD=80°，
则CD的度数是80°
⌒
注：不可写成CD = ∠COD=80°,
但可写成 CD = ∠COD=80°
⌒
⌒
m
如图：已知在⊙O中，∠AOB=45°, ∠OBC=35°
则AB的度数为 .
BC的度数为 .
⌒
⌒
巩固新知：
45
35
45°
110°
课堂小结：
1、圆是中心对称图形，圆具有旋转不变性；
2、圆心角定理：
3、弧的度数：1 的圆心角所对的弧叫做1 的弧.
在同圆或等圆中，
相等的圆心角所对的弧相等，　　　　　　　　
所对的弦相等，　　　　　　
所对弦的弦心距相等. 　　　
性质：弧的度数和它所对的圆心角的度数相等。
如图：点C为圆心，∠ACB=90°, ∠B=25°
求AD的度数
⌒
25
65
拓展延伸：
已知：AB为⊙O直径，AC∥OD，
且C、D在圆上。
求证：CD=BD
⌒
⌒
拓展延伸：
已知：AB=AC, ∠BAC=50°
求AB,BC,CA的度数
⌒
⌒
⌒
拓展延伸：