浙教版初中数学七年级上册第4章代数式 复 习 课 课件(26张)
文档属性
| 名称 | 浙教版初中数学七年级上册第4章代数式 复 习 课 课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 768.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
《第4章代数式》
复
习
课
请你写出三个代数式,要求在结构形式上尽可能的不同。
我们先来试一试
代数式的特点
(1)单独的一个数或一个字母也是代数式
(2)代数式中不含
“=”、“≠”、“≤”、“≥”
(3)数与数之间、数与字母之间、
字母与字母之间用运算符号连接。
小明的错题1
注意书写规范:
1.代数式中出现的乘号通常写成“·”或省
略不写;
2.数字与字母相乘时,数字写在字母的前面;
4.除法运算写成分数形式;
5.“1”和“-1”中的1常省略不写;
3.带分数与字母相乘时要化成假分数;
a+3米
(a+3)米
4n
6.后接单位的相加式子要用括号括起来。
求代数式3x?的值.
解:
①当
时,
②当
时,
上述解法对吗?如何改正.
小明错题2
具体书写过程:当、抄、代、算。
注意事项:
(1)代入数值时必须把原来省略的乘号添上;
(2)负数、分数代入时要根据情况适时加上括号;
(3)计算时,应注意运算顺序。
例1、用代数式表示:
(1)数a的2倍与数b的
的和。
(2)a与b的相反数的差的平方;
(3)a、b两数的平方差的3倍;
(4)x与y的倒数的差。
列代数式的关键在于弄清楚并正确表述语句所
反映的数量关系。
[a-(-b)]2
3(a2-b2)
a、b两数的差平方的3倍;
3(a-b)2
n
-3
-2
-1
0
1
2
3
4
5n+6
n2
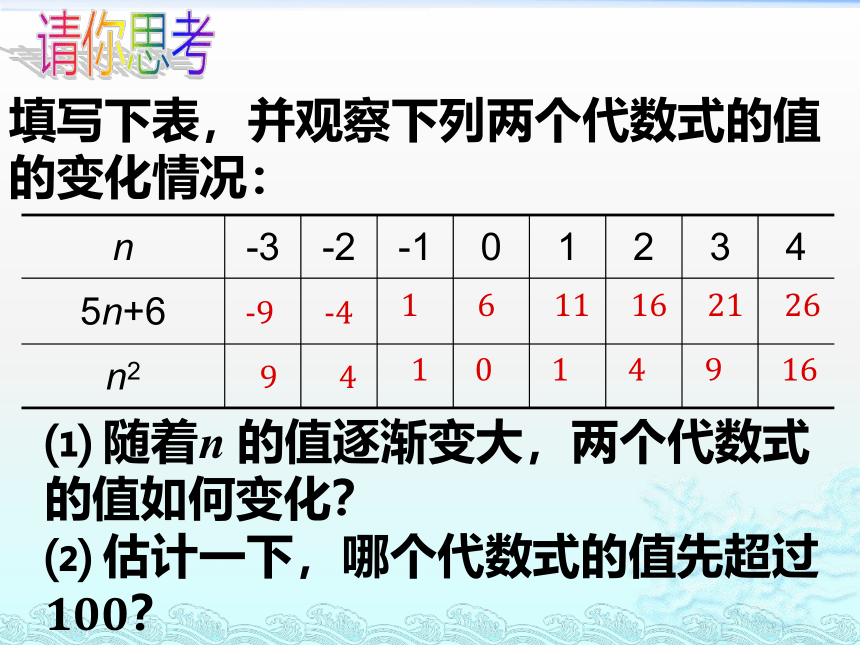
填写下表,并观察下列两个代数式的值
的变化情况:
请你思考
⑴
随着n
的值逐渐变大,两个代数式的值如何变化?
⑵
估计一下,哪个代数式的值先超过100?
-9
-4
1
6
11
16
21
26
9
4
1
0
1
4
9
16
1.
若
,则代数式
的值是
0或8
2.
若a-b=
-2,那么(a-b)2的值是
,
3a-3b+5的值是
4
–1
分类思想
拓展练习
整体思想
例2:现用20米的篱笆围成长方形的养鸡场,设养鸡场的长为x米。
(1)用代数式表示养鸡场的面积;
变式:如图,AB为墙,现用20米的篱笆围成长方形的养鸡场,设养鸡场的长为x米。
用代数式表示养鸡场的面积;
(2)当x分别为8,10,11时哪一种围法使养鸡场的面积最大?
小明错题3
由数与字母或字母与字母相乘组成的代数式
---------单项式
★
单独一个数或一个字母也叫单项式。如:0,-1,a等
整式:单项式和多项式
辩一辩
下列代数式中哪些是单项式,
√
√
√
(2)分母不含未知字母,
(3)根号内不含未知字母
注意:在单项式中
(1)只含乘法运算,不含加减运算
(1-20%)x
-2π
√
√
知识回顾
单项式中的数字因数,叫做这个单项式的系数.
练习2:指出以下单项式的系数:
3x2,-
x
2y2z,a2b,-2.15ab3,-m3,0,12h.
所有字母的指数和叫做这个单项式的次数。
说出单项式-3x?y?z的字母因数及各字母的指数分别是什么?这个单项式的次数是几次?
练习3、
指出下列单项式的次数:
2a2,-
x2,0.75ab2c,32a2b2,x5y?
由几个单项式相加组成的代数式
叫做多项式.
在多项式中,
每一个单项式叫做
。
不含字母的项叫做
.
这个多项式的项
常数项
多项式中次数最高的项的次数,
就是这个多项式的次数.
一个多项式的次数是几,
就称为几次多项式
-2x2+2x-5
由-2x2
;2x
;-5共三项组成
次数是二次
多项式的项数,次数
称二次多项式
项数是三项
称三项多项式
称二次三项式
一个多项式的项数是几,就是几项式;
练习1
(1)填表
多项式
项数
次数
常数项
最高次项
3x-7
X?-3x+4
ab-a?-1
2
3
3
2
1
2
2
2
-7
4
-1
0
3x
X?
ab和
-a?
b?
3
几个单项式的和
多项式
系
数
次
数
次
数
项
单项式
小明的错题
注意:1.
根号里含字母,分母里含字母都不是整式
3.
一个字母或一个数也是单项式。
注意:
③所有的常数项都是同类项.
同类项?
②与系数无关;
①字母相同,
与字母顺序无关.
相同字母的指数也分别相同;
小明错题2
分类
【探究活动1】什么是同类项
都含字母x和y,
并且x的指数都是2,
y
的指数都是1;
都是常数项
在多项式中所含字母相同,并且相同字母的指数也分别相同的项叫做同类项.
所有常数项也看做同类项.
合并同类项
把多项式中的同类项合并成一项叫做合并同类项
法
则
①把同类项的系数相加,所得的
结果作为新的系数;
②字母以及字母的指数不变。
一变
一不变
归纳总结让我们一起来
师生互动,牢记新知
涂涂做了4个题目,我们帮他看看,有需要改正或改进的地方吗?
不是同类项不能合并
字母以及字母的指数不能漏抄。
把同类项的系数相加,所得的结果作为新的系数;字母以及字母的指数不变。
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.所有常数项也看做同类项.
根据分配律,得
+(a+b-c)
=
1×(a+b-c)
=
a+b-c
-(a+b-c)
=
(-1)×(a+b-c)
=
-a-b+c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号;
顺口溜:
去括号,看符号
是’’+’’号,不变号
是“-”号,全变号
辩一辩:
指出下列各式是否正确?如果错误,请指出原因.
(错
a-b+c-d)
(错
a-3b+6c)
(错
x+2y+6z-2)
(1)a-(b-c+d)
=
a-b+c+d
(2)a-3(b-2c)=a-3b+2c
(3)x-2(-y-3z+1)=x-2y+6z
要注意括号前面是
“-“号时,去掉括号后,
括号里各项都要改变符号;不能只改变某几项而忘记改变其余的符号
若括号前面是数字因数时,应乘以括号里的每一项,不要漏乘.
例3、化简并求值:
2(a2-ab)-3(
a2-ab
),其中a=-2,b=3.
1、要掌握好此题的书写格式
2、整式的化简归结为去括号和
合并同类项
步骤:1、列式——整体思想
-2x
8x
0
练一练
1、(1)3x与-5x的和是__________,
3x与-5x的差是__________;
(2)a-b,b-c,c-a三个多项式的和
。
2.
求整式3a2b-ab2的5倍与ab2+3a2b的差。
4.已知3y-x=5,
则
2(x-3y)2-4(x-3y)-5=_______.
3.已知A=
3x+4y
,B=
2x-2y-1
,求
3A-2B
65
2、去括号——特别是“-”需注意
3、合并同类项——至不能合并为止
谢谢观看
《第4章代数式》
复
习
课
请你写出三个代数式,要求在结构形式上尽可能的不同。
我们先来试一试
代数式的特点
(1)单独的一个数或一个字母也是代数式
(2)代数式中不含
“=”、“≠”、“≤”、“≥”
(3)数与数之间、数与字母之间、
字母与字母之间用运算符号连接。
小明的错题1
注意书写规范:
1.代数式中出现的乘号通常写成“·”或省
略不写;
2.数字与字母相乘时,数字写在字母的前面;
4.除法运算写成分数形式;
5.“1”和“-1”中的1常省略不写;
3.带分数与字母相乘时要化成假分数;
a+3米
(a+3)米
4n
6.后接单位的相加式子要用括号括起来。
求代数式3x?的值.
解:
①当
时,
②当
时,
上述解法对吗?如何改正.
小明错题2
具体书写过程:当、抄、代、算。
注意事项:
(1)代入数值时必须把原来省略的乘号添上;
(2)负数、分数代入时要根据情况适时加上括号;
(3)计算时,应注意运算顺序。
例1、用代数式表示:
(1)数a的2倍与数b的
的和。
(2)a与b的相反数的差的平方;
(3)a、b两数的平方差的3倍;
(4)x与y的倒数的差。
列代数式的关键在于弄清楚并正确表述语句所
反映的数量关系。
[a-(-b)]2
3(a2-b2)
a、b两数的差平方的3倍;
3(a-b)2
n
-3
-2
-1
0
1
2
3
4
5n+6
n2
填写下表,并观察下列两个代数式的值
的变化情况:
请你思考
⑴
随着n
的值逐渐变大,两个代数式的值如何变化?
⑵
估计一下,哪个代数式的值先超过100?
-9
-4
1
6
11
16
21
26
9
4
1
0
1
4
9
16
1.
若
,则代数式
的值是
0或8
2.
若a-b=
-2,那么(a-b)2的值是
,
3a-3b+5的值是
4
–1
分类思想
拓展练习
整体思想
例2:现用20米的篱笆围成长方形的养鸡场,设养鸡场的长为x米。
(1)用代数式表示养鸡场的面积;
变式:如图,AB为墙,现用20米的篱笆围成长方形的养鸡场,设养鸡场的长为x米。
用代数式表示养鸡场的面积;
(2)当x分别为8,10,11时哪一种围法使养鸡场的面积最大?
小明错题3
由数与字母或字母与字母相乘组成的代数式
---------单项式
★
单独一个数或一个字母也叫单项式。如:0,-1,a等
整式:单项式和多项式
辩一辩
下列代数式中哪些是单项式,
√
√
√
(2)分母不含未知字母,
(3)根号内不含未知字母
注意:在单项式中
(1)只含乘法运算,不含加减运算
(1-20%)x
-2π
√
√
知识回顾
单项式中的数字因数,叫做这个单项式的系数.
练习2:指出以下单项式的系数:
3x2,-
x
2y2z,a2b,-2.15ab3,-m3,0,12h.
所有字母的指数和叫做这个单项式的次数。
说出单项式-3x?y?z的字母因数及各字母的指数分别是什么?这个单项式的次数是几次?
练习3、
指出下列单项式的次数:
2a2,-
x2,0.75ab2c,32a2b2,x5y?
由几个单项式相加组成的代数式
叫做多项式.
在多项式中,
每一个单项式叫做
。
不含字母的项叫做
.
这个多项式的项
常数项
多项式中次数最高的项的次数,
就是这个多项式的次数.
一个多项式的次数是几,
就称为几次多项式
-2x2+2x-5
由-2x2
;2x
;-5共三项组成
次数是二次
多项式的项数,次数
称二次多项式
项数是三项
称三项多项式
称二次三项式
一个多项式的项数是几,就是几项式;
练习1
(1)填表
多项式
项数
次数
常数项
最高次项
3x-7
X?-3x+4
ab-a?-1
2
3
3
2
1
2
2
2
-7
4
-1
0
3x
X?
ab和
-a?
b?
3
几个单项式的和
多项式
系
数
次
数
次
数
项
单项式
小明的错题
注意:1.
根号里含字母,分母里含字母都不是整式
3.
一个字母或一个数也是单项式。
注意:
③所有的常数项都是同类项.
同类项?
②与系数无关;
①字母相同,
与字母顺序无关.
相同字母的指数也分别相同;
小明错题2
分类
【探究活动1】什么是同类项
都含字母x和y,
并且x的指数都是2,
y
的指数都是1;
都是常数项
在多项式中所含字母相同,并且相同字母的指数也分别相同的项叫做同类项.
所有常数项也看做同类项.
合并同类项
把多项式中的同类项合并成一项叫做合并同类项
法
则
①把同类项的系数相加,所得的
结果作为新的系数;
②字母以及字母的指数不变。
一变
一不变
归纳总结让我们一起来
师生互动,牢记新知
涂涂做了4个题目,我们帮他看看,有需要改正或改进的地方吗?
不是同类项不能合并
字母以及字母的指数不能漏抄。
把同类项的系数相加,所得的结果作为新的系数;字母以及字母的指数不变。
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.所有常数项也看做同类项.
根据分配律,得
+(a+b-c)
=
1×(a+b-c)
=
a+b-c
-(a+b-c)
=
(-1)×(a+b-c)
=
-a-b+c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号;
顺口溜:
去括号,看符号
是’’+’’号,不变号
是“-”号,全变号
辩一辩:
指出下列各式是否正确?如果错误,请指出原因.
(错
a-b+c-d)
(错
a-3b+6c)
(错
x+2y+6z-2)
(1)a-(b-c+d)
=
a-b+c+d
(2)a-3(b-2c)=a-3b+2c
(3)x-2(-y-3z+1)=x-2y+6z
要注意括号前面是
“-“号时,去掉括号后,
括号里各项都要改变符号;不能只改变某几项而忘记改变其余的符号
若括号前面是数字因数时,应乘以括号里的每一项,不要漏乘.
例3、化简并求值:
2(a2-ab)-3(
a2-ab
),其中a=-2,b=3.
1、要掌握好此题的书写格式
2、整式的化简归结为去括号和
合并同类项
步骤:1、列式——整体思想
-2x
8x
0
练一练
1、(1)3x与-5x的和是__________,
3x与-5x的差是__________;
(2)a-b,b-c,c-a三个多项式的和
。
2.
求整式3a2b-ab2的5倍与ab2+3a2b的差。
4.已知3y-x=5,
则
2(x-3y)2-4(x-3y)-5=_______.
3.已知A=
3x+4y
,B=
2x-2y-1
,求
3A-2B
65
2、去括号——特别是“-”需注意
3、合并同类项——至不能合并为止
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
