浙教版七年级上册2.5有理数的乘方创新学案(无答案)
文档属性
| 名称 | 浙教版七年级上册2.5有理数的乘方创新学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 597.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 18:09:21 | ||
图片预览


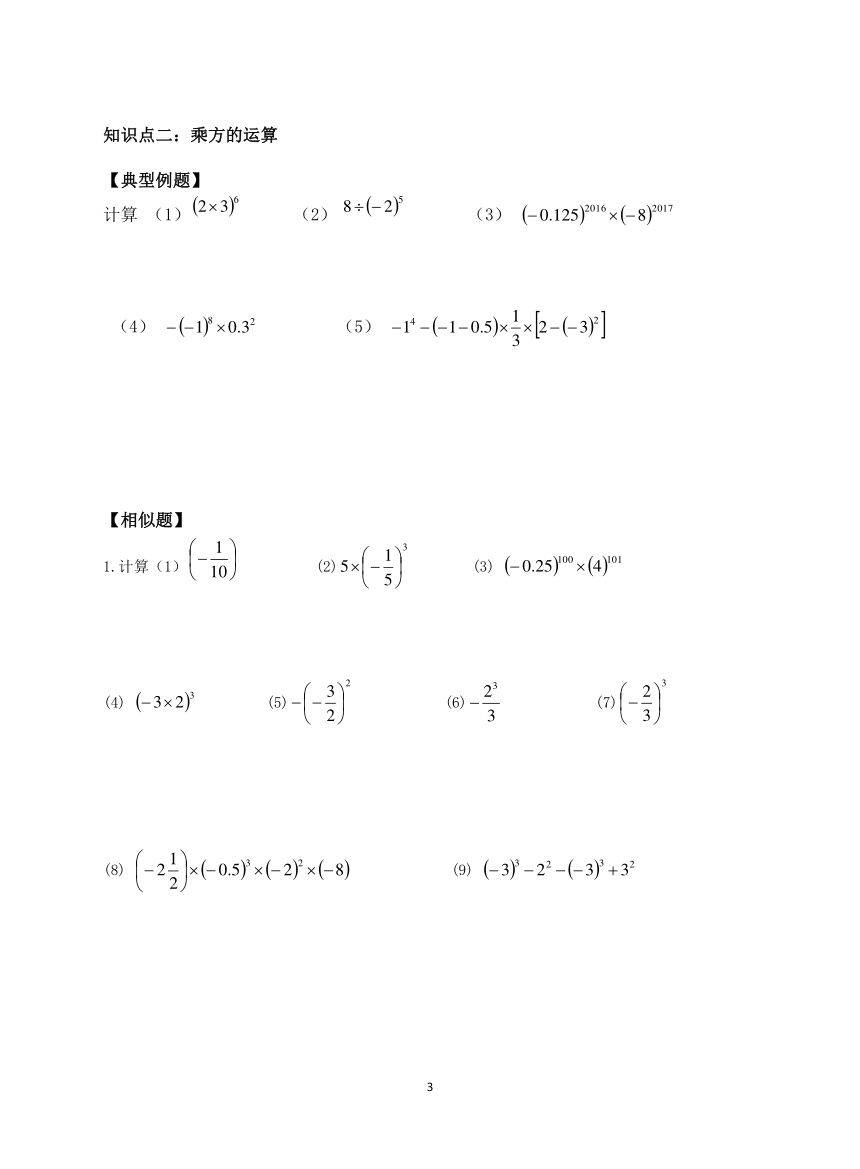
文档简介
有理数的乘方
【知识框架】
知识点一:有理数的乘方
1.求个相同因数的积的运算,叫做乘方。
2.乘方的结果叫做幂;用字母表示记作,其中叫做底数,叫做指数,的结果叫做幂;读法:读作的次方或的次幂。
3.正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数,零的任何正整数次幂都是零,没有意义;1的任何次幂都是1;-1的奇次幂都是-1;-1的偶次幂都是1.
4.一个数可以看成这个数本身的一次放,例如5就是,
就是,指数1通常省略不写。
5.要分清和和的联系和区别。
6.10的次方等于在1后面补个0,0.1的次方等于1前面个0的小数,负数的偶次方为正,奇次方为负。两个数互为相反数,偶次方相等,奇次方互为相反数。
【典型例题1】
1.
把下列各式写成乘方运算的形式,并指出底数、指数各是什么?
(1)(-1.3)·(-1.3)·(-1.3)·(-1.3)
(2)×××××
【相似题】
1.
写成乘方形式是 .
2.在中,底数是 ,指数是 ,幂是 .
3.在中,底数是 ,指数是 ,结果是 .
4.底数是-2,指数是2的幂写作 ,其结果是 .
【典型例题2】
计算
=
,
= ,
=
,
=
;(为正整数)
=
,
=
,
=
,
=
(为正整数)
【相似题】
1.观察下列各式,回答下列问题.
,,,,,,,
(1)当底数的小数点向左(或向右)移动一位时,其平方数的小数点向左(或向右)移动几位?
(2)当底数的小数点向左(或向右)移动一位时,其立方数的小数点向左(或向右)移动几位?
2.根据乘方的意义可知:,,
则即.想一想:
(1) (其中都是正整数).
(2) .
知识点二:乘方的运算
【典型例题】
计算
(1)
(2)
(3)
(4)
(5)
【相似题】
1.计算(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
2.已知.
(1)当是最小的正整数时,求的值;
(2)当是最大的负整数时,求的值.
3.根据乘方的意义可知:,,
则即.想一想:
(1) (其中都是正整数).
(2) .
4.在数学活动中,小明为了求+的值(结果用n表示),设计了如图
所示的几何图形.
(1)请你利用这个几何图形求+的值为________;
(2)请你利用如图(2)所示,再设计一个能求+的值的几种图形.
知识点三:乘方的应用
例1.如图所示,面积为1的长方形纸片第1次裁去一半,第2次裁去剩下的一半,如此裁下去,第8次裁剪后剩下纸片的面积是____.
例2.有一张厚度是0.1
mm的纸,将它对折1次后,厚度为2×0.1
mm.
(1)对折2次后,厚度为多少毫米?
(2)每层楼平均高度为3
m,这张纸对折20次后有多少层楼高?(提示:220=1
048
576)
例3.
1米长的小棒,第一次截去一半,第二次截去剩下的一半,如此截下去,第7次后,剩下的小棒有多长?
例4.看过电视剧《西游记》的同学一定很喜欢孙悟空的金箍棒,能随意伸缩.假设它最短时只有1厘米,第一次变化后为3厘米,第二次变化后为9厘米,第三次变化后为27厘米……照此规律变下去,到第几次变化后才能得到使用方便的2.43米?
【巩固练习】
1.
表示
(
)
A.8个-5相乘
B.
5个-8相乘
C.
8个5相乘的相反数
D.
5个8相乘的相反数
2.若,则的绝对值是
(
)
A.2
B.-2
C.
D.-
3.下列各组数中数值相等的是
(
)
A.与
B.与
C.与
D.与
4.计算的结果是(
)
A.1
B.-1
C.0
D.2
5.对于乘积(-3)×(-3)×(-3)×(-3)写成乘方的形式为
;
6.表示
个
相乘,底数是
,指数是
;
7.一个数的平方后仍得它本身的数是
;
的平方等于16.
8.=
;=
;
=
;
=
;
=
;=
;=
;=
;
9.计算
(1)
(2)
(3)
(4)
(5)
10.如图下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…照此规律,图A6比图A2多出“树枝”( )
A.28个
B.56个
C.60个
D.124个
11.某种细胞每过30分便由1个分裂成2个,经过5时,这种细胞由一个分裂成了多少个?
12.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒,16粒,32粒……一直到第64格.”“你真傻!就要这么一点米粒?!”国王哈哈大笑.
(1)在第64格中应放多少米?(用幂表示)
(2)请探究(1)中的数的末位数字是多少?(简要写出探究过程)
(3)求国王应给这位大臣多少米.
【知识框架】
知识点一:有理数的乘方
1.求个相同因数的积的运算,叫做乘方。
2.乘方的结果叫做幂;用字母表示记作,其中叫做底数,叫做指数,的结果叫做幂;读法:读作的次方或的次幂。
3.正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数,零的任何正整数次幂都是零,没有意义;1的任何次幂都是1;-1的奇次幂都是-1;-1的偶次幂都是1.
4.一个数可以看成这个数本身的一次放,例如5就是,
就是,指数1通常省略不写。
5.要分清和和的联系和区别。
6.10的次方等于在1后面补个0,0.1的次方等于1前面个0的小数,负数的偶次方为正,奇次方为负。两个数互为相反数,偶次方相等,奇次方互为相反数。
【典型例题1】
1.
把下列各式写成乘方运算的形式,并指出底数、指数各是什么?
(1)(-1.3)·(-1.3)·(-1.3)·(-1.3)
(2)×××××
【相似题】
1.
写成乘方形式是 .
2.在中,底数是 ,指数是 ,幂是 .
3.在中,底数是 ,指数是 ,结果是 .
4.底数是-2,指数是2的幂写作 ,其结果是 .
【典型例题2】
计算
=
,
= ,
=
,
=
;(为正整数)
=
,
=
,
=
,
=
(为正整数)
【相似题】
1.观察下列各式,回答下列问题.
,,,,,,,
(1)当底数的小数点向左(或向右)移动一位时,其平方数的小数点向左(或向右)移动几位?
(2)当底数的小数点向左(或向右)移动一位时,其立方数的小数点向左(或向右)移动几位?
2.根据乘方的意义可知:,,
则即.想一想:
(1) (其中都是正整数).
(2) .
知识点二:乘方的运算
【典型例题】
计算
(1)
(2)
(3)
(4)
(5)
【相似题】
1.计算(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
2.已知.
(1)当是最小的正整数时,求的值;
(2)当是最大的负整数时,求的值.
3.根据乘方的意义可知:,,
则即.想一想:
(1) (其中都是正整数).
(2) .
4.在数学活动中,小明为了求+的值(结果用n表示),设计了如图
所示的几何图形.
(1)请你利用这个几何图形求+的值为________;
(2)请你利用如图(2)所示,再设计一个能求+的值的几种图形.
知识点三:乘方的应用
例1.如图所示,面积为1的长方形纸片第1次裁去一半,第2次裁去剩下的一半,如此裁下去,第8次裁剪后剩下纸片的面积是____.
例2.有一张厚度是0.1
mm的纸,将它对折1次后,厚度为2×0.1
mm.
(1)对折2次后,厚度为多少毫米?
(2)每层楼平均高度为3
m,这张纸对折20次后有多少层楼高?(提示:220=1
048
576)
例3.
1米长的小棒,第一次截去一半,第二次截去剩下的一半,如此截下去,第7次后,剩下的小棒有多长?
例4.看过电视剧《西游记》的同学一定很喜欢孙悟空的金箍棒,能随意伸缩.假设它最短时只有1厘米,第一次变化后为3厘米,第二次变化后为9厘米,第三次变化后为27厘米……照此规律变下去,到第几次变化后才能得到使用方便的2.43米?
【巩固练习】
1.
表示
(
)
A.8个-5相乘
B.
5个-8相乘
C.
8个5相乘的相反数
D.
5个8相乘的相反数
2.若,则的绝对值是
(
)
A.2
B.-2
C.
D.-
3.下列各组数中数值相等的是
(
)
A.与
B.与
C.与
D.与
4.计算的结果是(
)
A.1
B.-1
C.0
D.2
5.对于乘积(-3)×(-3)×(-3)×(-3)写成乘方的形式为
;
6.表示
个
相乘,底数是
,指数是
;
7.一个数的平方后仍得它本身的数是
;
的平方等于16.
8.=
;=
;
=
;
=
;
=
;=
;=
;=
;
9.计算
(1)
(2)
(3)
(4)
(5)
10.如图下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…照此规律,图A6比图A2多出“树枝”( )
A.28个
B.56个
C.60个
D.124个
11.某种细胞每过30分便由1个分裂成2个,经过5时,这种细胞由一个分裂成了多少个?
12.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒,16粒,32粒……一直到第64格.”“你真傻!就要这么一点米粒?!”国王哈哈大笑.
(1)在第64格中应放多少米?(用幂表示)
(2)请探究(1)中的数的末位数字是多少?(简要写出探究过程)
(3)求国王应给这位大臣多少米.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
