4.2 由平行线截得的比例线段
图片预览



文档简介
(共25张PPT)
4.2
由平行线截得的比例线段
一.活动与思考:
1.观察练习簿的横格线,你发现有什么特征?
互相平行
间隔距离相等
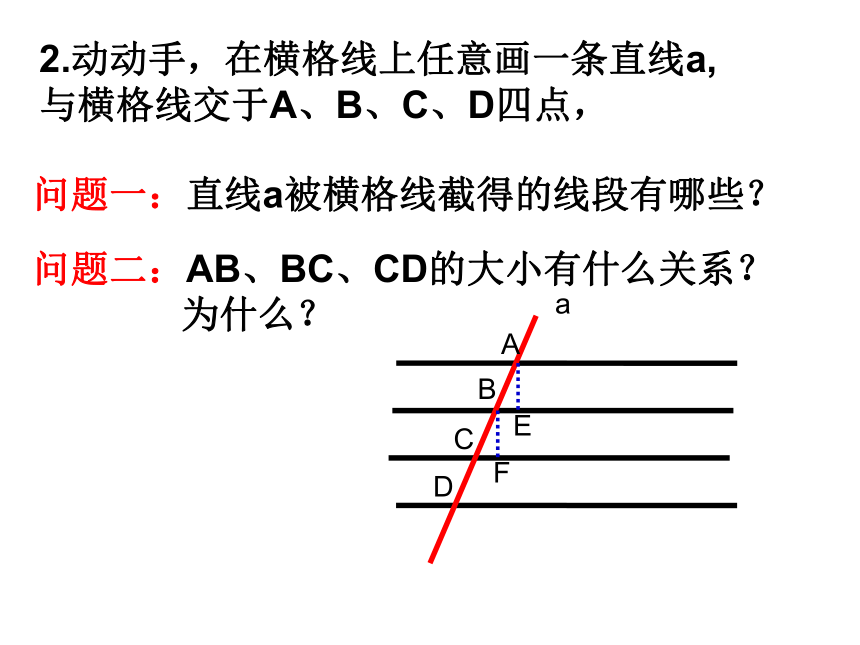
2.动动手,在横格线上任意画一条直线a,
与横格线交于A、B、C、D四点,
问题一:直线a被横格线截得的线段有哪些?
问题二:AB、BC、CD的大小有什么关系?
为什么?
a
A
D
B
C
E
F
问题三:你能求出以下线段的比值吗?
你还可以求出哪些线段的比值?
a
A
D
B
C
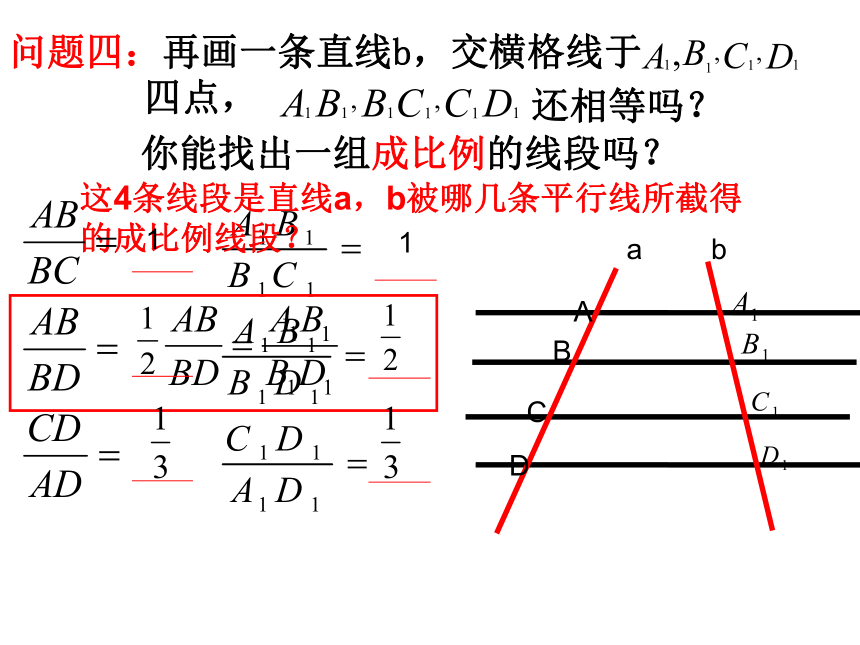
问题四:再画一条直线b,交横格线于
四点,
还相等吗?
a
b
A
D
B
C
1
你能找出一组成比例的线段吗?
这4条线段是直线a,b被哪几条平行线所截得
的成比例线段?
1
a
b
A
D
B
C
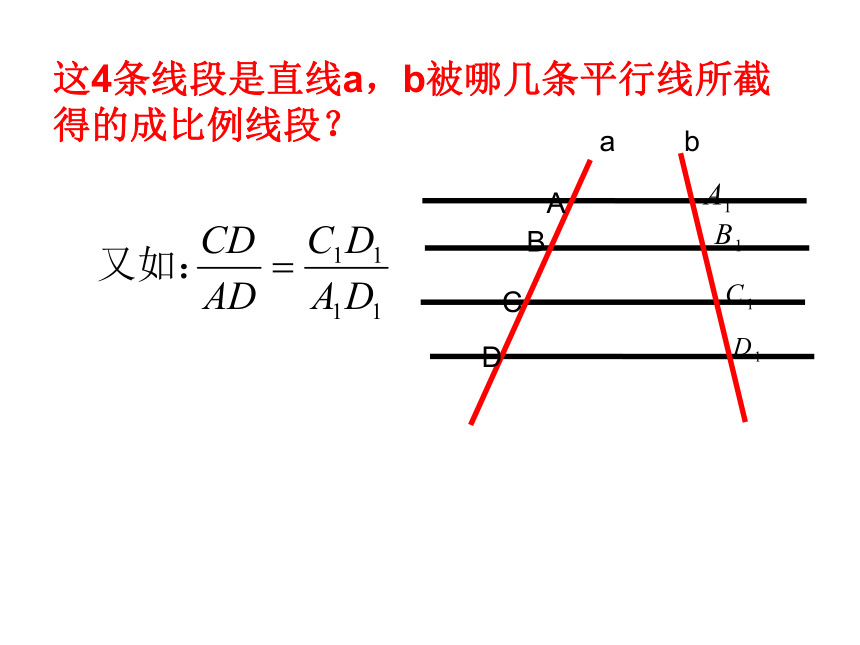
这4条线段是直线a,b被哪几条平行线所截得的成比例线段?
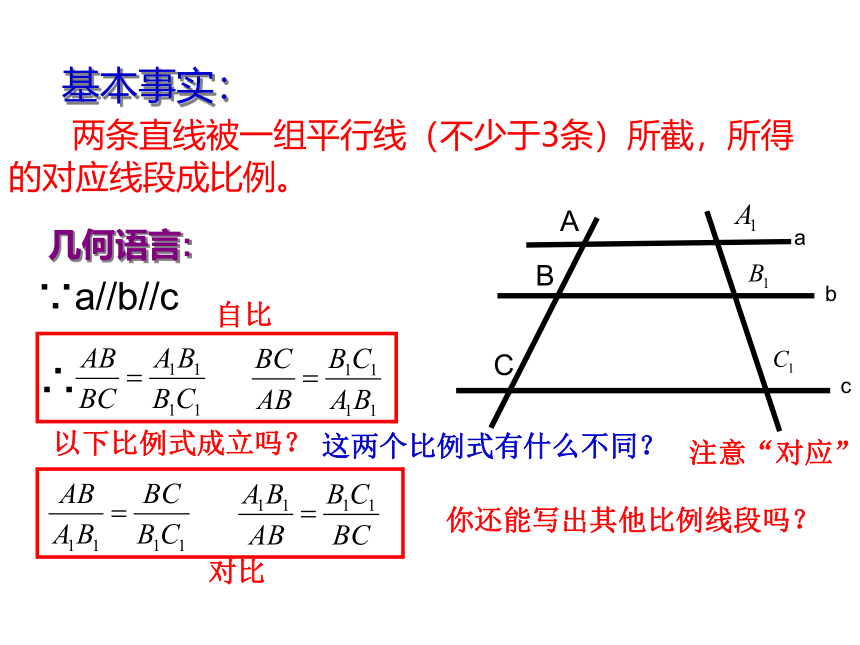
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例。
A
B
C
a
b
c
∵a//b//c
几何语言:
基本事实:
∴
以下比例式成立吗?
自比
对比
你还能写出其他比例线段吗?
注意“对应”
这两个比例式有什么不同?
A
B
C
a
b
c
注意“对应”
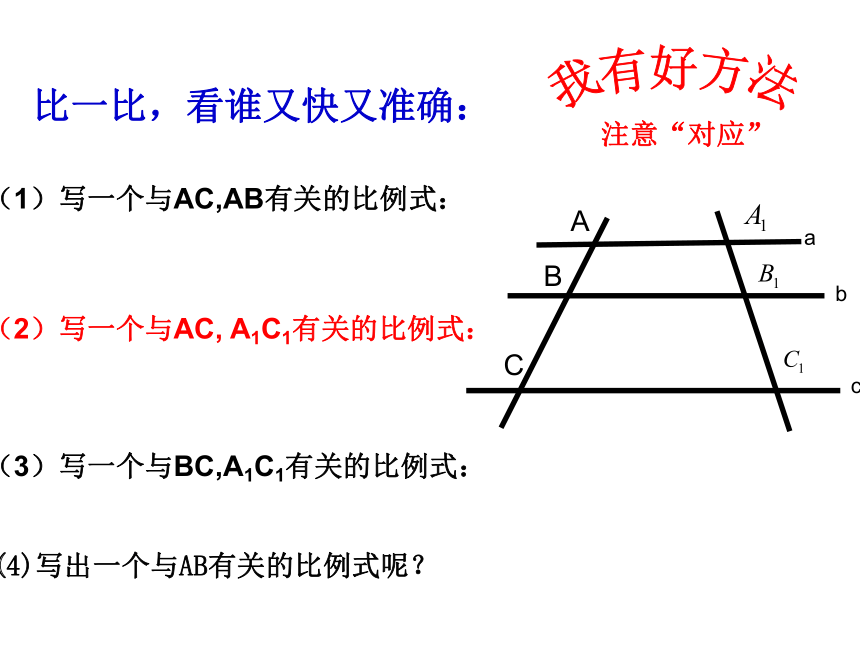
(1)写一个与AC,AB有关的比例式:
(2)写一个与AC,
A1C1有关的比例式:
比一比,看谁又快又准确:
(3)写一个与BC,A1C1有关的比例式:
我有好方法
(4)写出一个与AB有关的比例式呢?
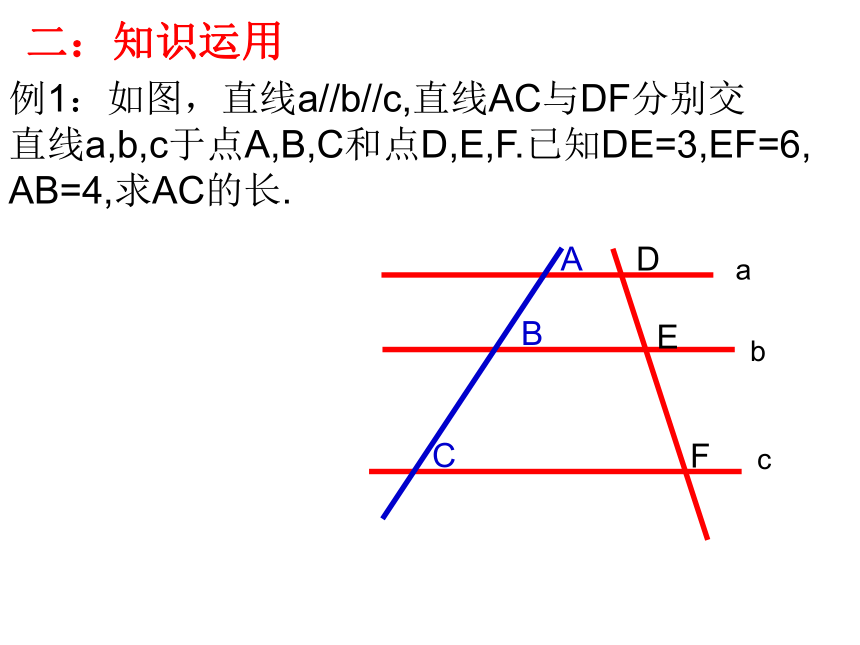
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
△ABC中,BE//CF,已知AE=3,EF=6,AB=4,
求AC的长.
变式跟进1:
A
B
C
E
F
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
A字型
A
B
C
E
F
解:过A点作直线AD//BE
∵
BE//CF,
∴
AD//BE//CF
∴
又∵AE=3,EF=6,AB=4
∴
∴BC=8,
∴
AC=12
D
△ABC中,BE//CF,已知AE=3,EF=6,AB=4,
求AC的长.
变式跟进1:
变式跟进2:
如图,AD//CF,已知DE=3,EF=6,AE
=4,
求AC的长.
A
E
C
D
F
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
8字型
A
E
D
F
C
解:
过E点作直线BE//
AD
∵
BE//CF,
∴
AD//BE//CF
∴
又∵AE=4,DE=3,EF=6
∴
∴EC=8
∴AC=12.
变式跟进2:
如图,AD//CF,已知DE=3,EF=6,AE
=4,
求AC的长.
B
A字型
8字型
这2个图形是以后解决相似三角形的有关计算和证明的
模具,以后我们会经常构造或寻找A字型或8字型解决问题.
A
B
C
M
N
1.如图,在△ABC中,MN//BC,AM=NC,AN=3,
MB=2,则NC=
三.课堂练习:
2.已知:AB与CD相交于点E,BC//EF//AD,
E
D
A
B
C
F
3.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等
于
(
)21世纪教育网版权所有
???A.5∶8
B.3∶8
C.3∶5
D.2∶5
教学目标
巩固提升
?
21cnjy.com
21cnjy.com
21cnjy.com
?
教学目标
巩固提升
A字型
A
B
C
D
E
例2:我们已经学习了中位线定理:
如果点D和点E分别是AB,AC的中点,那么DE//BC,
下面我们对以下问题进行猜想:
猜想1:
若点D是AB的中点,DE//BC,
那么点E是否是AC的中点?
猜想2:
若点D是AB的三等分点,DE//BC,
那么点E是否是AC的三等分点?
猜想3:
当点D是AB的四等分点,
五等分点……n等分点时,结果又怎样呢?
你发现了什么?
跟进与提高:已知线段MN,把线段MN五等分.
M
N
只要D首先满足是线段AB的n等分点,再过D点作DE//BC,
交AC于E点,则E必定也是另一条线段AC的n等分点.
跟进与提高:已知线段MN,把线段MN五等分.
如果把线段MN分成2:3的两部分,又该怎么分呢?
M
N
E
1.以M为端点作一条射线,并在射线上依次截取线段
MA=AB=BC=CD=DE
A
B
C
D
2.连接NE,并过A,B,C,D,分别作NE的平行线,
依次交MN于点F,G,H,I.(或者只作一条平行线AF,
然后依次在MN上截取FG=GH=HI=MF)
F
G
H
I
作法:
点F,G,H,I就是所求作的把
线段MN五等分的点.
如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )
A.5∶8
B.3∶8
C.3∶5
D.2∶5
教学目标
巩固提升
A
?
教学目标
巩固提升
A
21cnjy.com
21cnjy.com
21cnjy.com
?
教学目标
巩固提升
2.5
教学目标
课堂小结
由平行线截得的比例线段
三条平行线截两条直线,所得的对应线段成比例.
平行线等分线段定理:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论:
4.2
由平行线截得的比例线段
一.活动与思考:
1.观察练习簿的横格线,你发现有什么特征?
互相平行
间隔距离相等
2.动动手,在横格线上任意画一条直线a,
与横格线交于A、B、C、D四点,
问题一:直线a被横格线截得的线段有哪些?
问题二:AB、BC、CD的大小有什么关系?
为什么?
a
A
D
B
C
E
F
问题三:你能求出以下线段的比值吗?
你还可以求出哪些线段的比值?
a
A
D
B
C
问题四:再画一条直线b,交横格线于
四点,
还相等吗?
a
b
A
D
B
C
1
你能找出一组成比例的线段吗?
这4条线段是直线a,b被哪几条平行线所截得
的成比例线段?
1
a
b
A
D
B
C
这4条线段是直线a,b被哪几条平行线所截得的成比例线段?
两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例。
A
B
C
a
b
c
∵a//b//c
几何语言:
基本事实:
∴
以下比例式成立吗?
自比
对比
你还能写出其他比例线段吗?
注意“对应”
这两个比例式有什么不同?
A
B
C
a
b
c
注意“对应”
(1)写一个与AC,AB有关的比例式:
(2)写一个与AC,
A1C1有关的比例式:
比一比,看谁又快又准确:
(3)写一个与BC,A1C1有关的比例式:
我有好方法
(4)写出一个与AB有关的比例式呢?
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
△ABC中,BE//CF,已知AE=3,EF=6,AB=4,
求AC的长.
变式跟进1:
A
B
C
E
F
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
A字型
A
B
C
E
F
解:过A点作直线AD//BE
∵
BE//CF,
∴
AD//BE//CF
∴
又∵AE=3,EF=6,AB=4
∴
∴BC=8,
∴
AC=12
D
△ABC中,BE//CF,已知AE=3,EF=6,AB=4,
求AC的长.
变式跟进1:
变式跟进2:
如图,AD//CF,已知DE=3,EF=6,AE
=4,
求AC的长.
A
E
C
D
F
例1:如图,直线a//b//c,直线AC与DF分别交
直线a,b,c于点A,B,C和点D,E,F.已知DE=3,EF=6,
AB=4,求AC的长.
A
B
C
a
b
c
D
E
F
二:知识运用
8字型
A
E
D
F
C
解:
过E点作直线BE//
AD
∵
BE//CF,
∴
AD//BE//CF
∴
又∵AE=4,DE=3,EF=6
∴
∴EC=8
∴AC=12.
变式跟进2:
如图,AD//CF,已知DE=3,EF=6,AE
=4,
求AC的长.
B
A字型
8字型
这2个图形是以后解决相似三角形的有关计算和证明的
模具,以后我们会经常构造或寻找A字型或8字型解决问题.
A
B
C
M
N
1.如图,在△ABC中,MN//BC,AM=NC,AN=3,
MB=2,则NC=
三.课堂练习:
2.已知:AB与CD相交于点E,BC//EF//AD,
E
D
A
B
C
F
3.如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等
于
(
)21世纪教育网版权所有
???A.5∶8
B.3∶8
C.3∶5
D.2∶5
教学目标
巩固提升
?
21cnjy.com
21cnjy.com
21cnjy.com
?
教学目标
巩固提升
A字型
A
B
C
D
E
例2:我们已经学习了中位线定理:
如果点D和点E分别是AB,AC的中点,那么DE//BC,
下面我们对以下问题进行猜想:
猜想1:
若点D是AB的中点,DE//BC,
那么点E是否是AC的中点?
猜想2:
若点D是AB的三等分点,DE//BC,
那么点E是否是AC的三等分点?
猜想3:
当点D是AB的四等分点,
五等分点……n等分点时,结果又怎样呢?
你发现了什么?
跟进与提高:已知线段MN,把线段MN五等分.
M
N
只要D首先满足是线段AB的n等分点,再过D点作DE//BC,
交AC于E点,则E必定也是另一条线段AC的n等分点.
跟进与提高:已知线段MN,把线段MN五等分.
如果把线段MN分成2:3的两部分,又该怎么分呢?
M
N
E
1.以M为端点作一条射线,并在射线上依次截取线段
MA=AB=BC=CD=DE
A
B
C
D
2.连接NE,并过A,B,C,D,分别作NE的平行线,
依次交MN于点F,G,H,I.(或者只作一条平行线AF,
然后依次在MN上截取FG=GH=HI=MF)
F
G
H
I
作法:
点F,G,H,I就是所求作的把
线段MN五等分的点.
如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )
A.5∶8
B.3∶8
C.3∶5
D.2∶5
教学目标
巩固提升
A
?
教学目标
巩固提升
A
21cnjy.com
21cnjy.com
21cnjy.com
?
教学目标
巩固提升
2.5
教学目标
课堂小结
由平行线截得的比例线段
三条平行线截两条直线,所得的对应线段成比例.
平行线等分线段定理:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论:
同课章节目录
