4.3相似三角形(共20张ppt)
图片预览




文档简介
(共20张PPT)
经过相似变换后得到的像与原像称为相似图形.
那么,将一个三角形作相似变换后所得到的像与原像称为相似三角形.
4.3
相似三角形
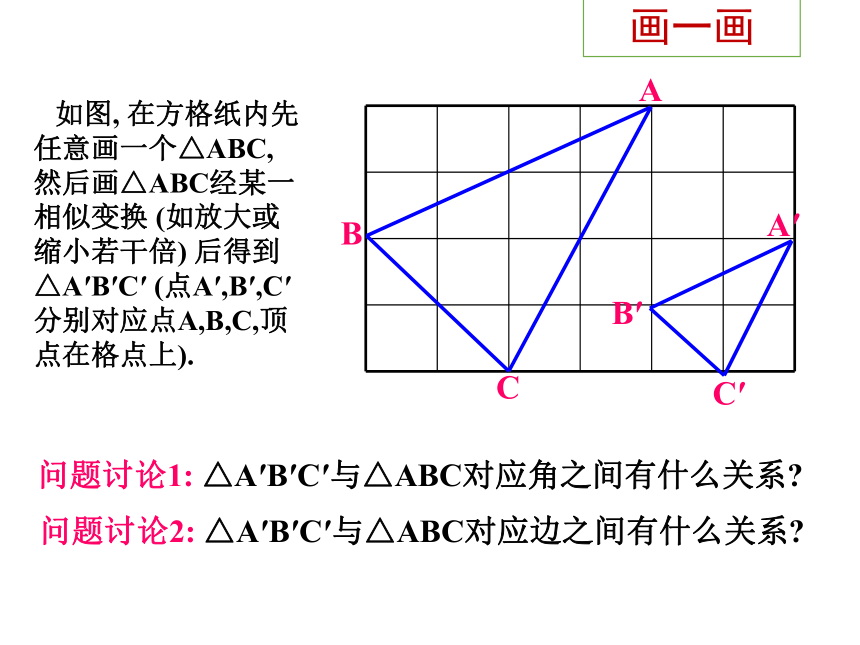
如图,
在方格纸内先任意画一个△ABC,
然后画△ABC经某一相似变换
(如放大或缩小若干倍)
后得到△A′B′C′
(点A′,B′,C′分别对应点A,B,C,顶点在格点上).
问题讨论1:
△A′B′C′与△ABC对应角之间有什么关系?
问题讨论2:
△A′B′C′与△ABC对应边之间有什么关系?
C
A
B
B′
A′
C′
画一画
C
A
B
B′
A′
C′
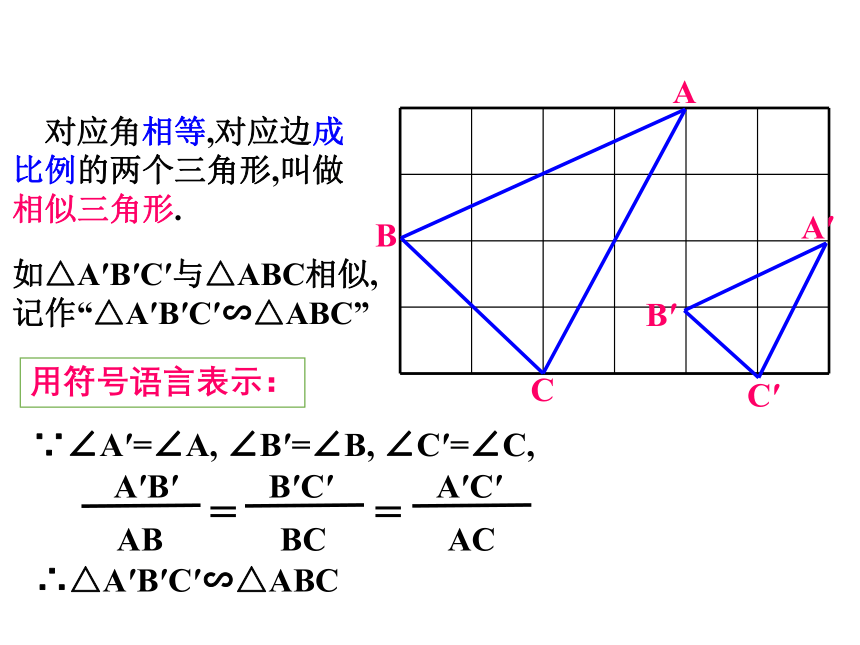
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似用符号“∽”来表示,
读做“相似于”
如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC”
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上.
C
A
B
B′
A′
C′
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC”
∵∠A′=∠A,
∠B′=∠B,
∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
用符号语言表示:
C
A
B
B′
A′
C′
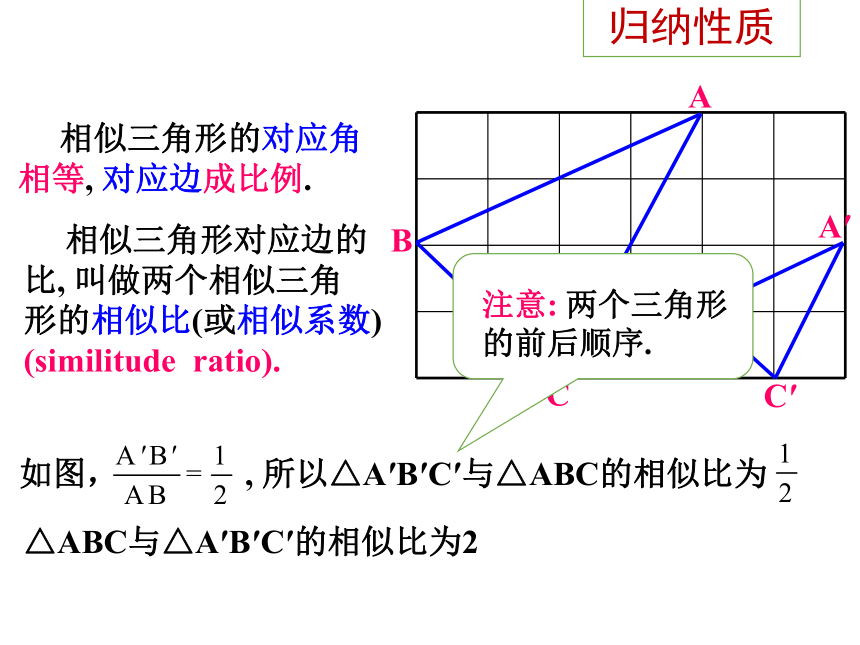
相似三角形的对应角相等,
对应边成比例.
相似三角形对应边的比,
叫做两个相似三角形的相似比(或相似系数)
(similitude
ratio).
△ABC与△A′B′C′的相似比为2
注意:
两个三角形的前后顺序.
如图,
,
所以△A′B′C′与△ABC的相似比为
归纳性质
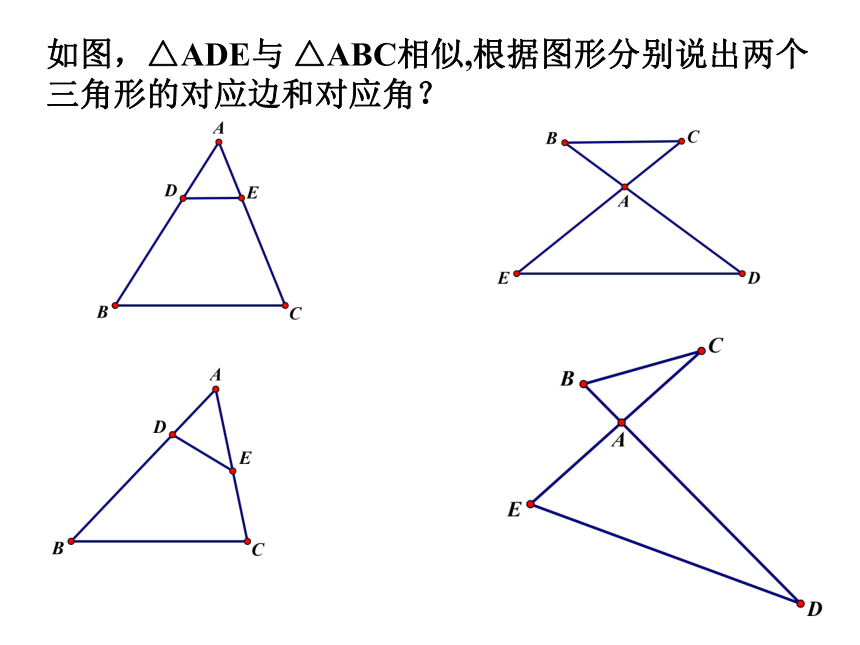
如图,△ADE与
△ABC相似,根据图形分别说出两个三角形的对应边和对应角?
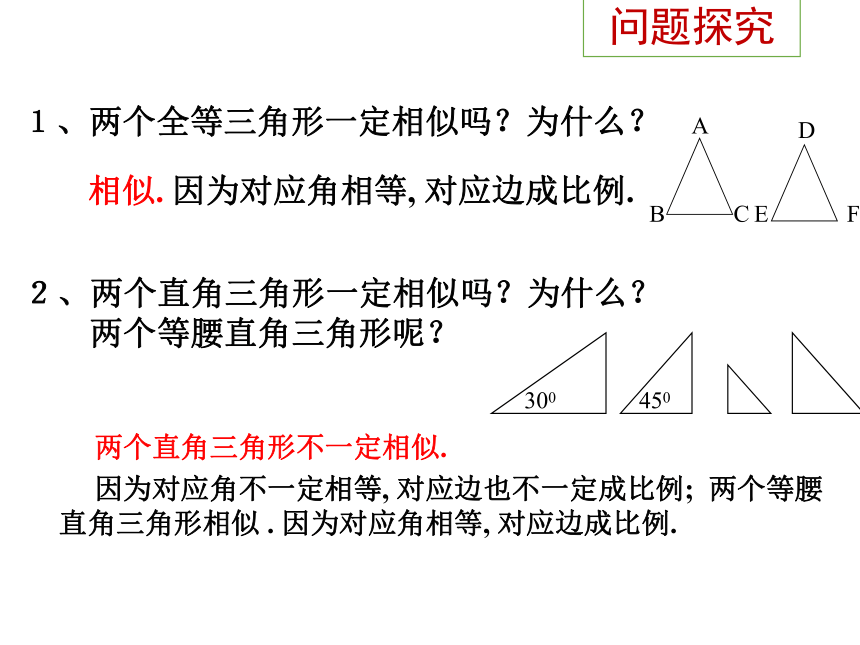
1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
B
C
D
E
F
A
300
450
相似.
因为对应角相等,
对应边成比例.
两个直角三角形不一定相似.
因为对应角不一定相等,
对应边也不一定成比例;
两个等腰直角三角形相似
.
因为对应角相等,
对应边成比例.
问题探究
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
B
C
D
E
F
A
两个等腰三角形不一定相似;
两个等边三角形相似.
例1:已知:如图,
D,
E分别是AB,
AC边的中点.
求证:
△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE=
BC.
∴△ADE∽△ABC
(相似三角形的定义)
例题探究
A
B
C
D
E
F
思考题:图中有几个三角形相似?
已知:D、E、F分别是三角形三边的中点.
相似三角形的传递性:如果△ABC∽△A1B1C1
,
而△A1B1C1
∽△A2B2C2
那么△ABC∽△A2B2C2
.
如果△ABC∽△A1B1C1
而△A1B1C1
∽△A2B2C2
那么△ABC与△A2B2C2
是否相似?为什么?
例2、已知:
如图,
D、E分别是△ABC的AB,
AC边上的点,
△ABC∽△ADE.
已知
AD:DB=1:2,
BC=9cm,
求DE的长.
E
D
C
B
A
温馨提醒:
AD:DB的比是△ADE与△ABC的相似比吗?
DE=9
1、已知△ABC与△DEF相似,
△ABC的三边为2,3,4,
△DEF的最大边为8,
求其余两边.
2、已知△ABC与△DEF相似,
△ABC的三边为2,3,4,
△DEF的一边为8,
求其余两边.
4,
6
4,6或12,16或16/3,32/3
探究活动
在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.
x
y
4
-1
-1
4
3
2
1
3
0
1
2
A
-4
-3
-2
-4
-3
-2
B
5
-5
1.作一个格点三角形与△OAB全等.
2.作一个格点三角形与△OAB相似.
3.作一个格点三角形与△OAB相似且与△OAB
共边AB.
●
1、在下面的两组图形中,各有两个相似三角形,试确定x
,y
,
m
,n
的值.
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
(1)
(2)
A
B
C
D
E
A
B
C
D
E
F
课堂练习
2、如图,
△ABC∽△ACD,点D在AB上,
已知
AC=3cm,
AD=2cm,
(1)
求AB的长.
(2)
若BC=5cm
,则CD=?
AB=4.5
CD=
3、已知在Rt△ABC中,∠ACB=Rt∠,AC=BC,CD⊥AB于D
求证:
△ACD∽△ABC.
改:若在Rt△ABC中,∠ACB=Rt∠,
CD⊥AB于D
且∠A=300
则△ACD∽△ABC?
△ACD与△CBD呢?
三个角对应相等,
三条边对应成比例的两个三角形,
叫做相似三角形(similar
trianglec).
△ABC与△DEF相似,
就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
性质:相似三角形的各对应角相等,各对应边对应成比例.
如果△
ABC∽
△DEF,
那么∠A
=
∠D,∠B
=
∠E,
∠C
=
∠F.
课堂小结
经过相似变换后得到的像与原像称为相似图形.
那么,将一个三角形作相似变换后所得到的像与原像称为相似三角形.
4.3
相似三角形
如图,
在方格纸内先任意画一个△ABC,
然后画△ABC经某一相似变换
(如放大或缩小若干倍)
后得到△A′B′C′
(点A′,B′,C′分别对应点A,B,C,顶点在格点上).
问题讨论1:
△A′B′C′与△ABC对应角之间有什么关系?
问题讨论2:
△A′B′C′与△ABC对应边之间有什么关系?
C
A
B
B′
A′
C′
画一画
C
A
B
B′
A′
C′
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似用符号“∽”来表示,
读做“相似于”
如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC”
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上.
C
A
B
B′
A′
C′
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC”
∵∠A′=∠A,
∠B′=∠B,
∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
用符号语言表示:
C
A
B
B′
A′
C′
相似三角形的对应角相等,
对应边成比例.
相似三角形对应边的比,
叫做两个相似三角形的相似比(或相似系数)
(similitude
ratio).
△ABC与△A′B′C′的相似比为2
注意:
两个三角形的前后顺序.
如图,
,
所以△A′B′C′与△ABC的相似比为
归纳性质
如图,△ADE与
△ABC相似,根据图形分别说出两个三角形的对应边和对应角?
1、两个全等三角形一定相似吗?为什么?
2、两个直角三角形一定相似吗?为什么?
两个等腰直角三角形呢?
B
C
D
E
F
A
300
450
相似.
因为对应角相等,
对应边成比例.
两个直角三角形不一定相似.
因为对应角不一定相等,
对应边也不一定成比例;
两个等腰直角三角形相似
.
因为对应角相等,
对应边成比例.
问题探究
3、两个等腰三角形一定相似吗?为什么?
两个等边三角形呢?
B
C
D
E
F
A
两个等腰三角形不一定相似;
两个等边三角形相似.
例1:已知:如图,
D,
E分别是AB,
AC边的中点.
求证:
△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE=
BC.
∴△ADE∽△ABC
(相似三角形的定义)
例题探究
A
B
C
D
E
F
思考题:图中有几个三角形相似?
已知:D、E、F分别是三角形三边的中点.
相似三角形的传递性:如果△ABC∽△A1B1C1
,
而△A1B1C1
∽△A2B2C2
那么△ABC∽△A2B2C2
.
如果△ABC∽△A1B1C1
而△A1B1C1
∽△A2B2C2
那么△ABC与△A2B2C2
是否相似?为什么?
例2、已知:
如图,
D、E分别是△ABC的AB,
AC边上的点,
△ABC∽△ADE.
已知
AD:DB=1:2,
BC=9cm,
求DE的长.
E
D
C
B
A
温馨提醒:
AD:DB的比是△ADE与△ABC的相似比吗?
DE=9
1、已知△ABC与△DEF相似,
△ABC的三边为2,3,4,
△DEF的最大边为8,
求其余两边.
2、已知△ABC与△DEF相似,
△ABC的三边为2,3,4,
△DEF的一边为8,
求其余两边.
4,
6
4,6或12,16或16/3,32/3
探究活动
在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.
x
y
4
-1
-1
4
3
2
1
3
0
1
2
A
-4
-3
-2
-4
-3
-2
B
5
-5
1.作一个格点三角形与△OAB全等.
2.作一个格点三角形与△OAB相似.
3.作一个格点三角形与△OAB相似且与△OAB
共边AB.
●
1、在下面的两组图形中,各有两个相似三角形,试确定x
,y
,
m
,n
的值.
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
(1)
(2)
A
B
C
D
E
A
B
C
D
E
F
课堂练习
2、如图,
△ABC∽△ACD,点D在AB上,
已知
AC=3cm,
AD=2cm,
(1)
求AB的长.
(2)
若BC=5cm
,则CD=?
AB=4.5
CD=
3、已知在Rt△ABC中,∠ACB=Rt∠,AC=BC,CD⊥AB于D
求证:
△ACD∽△ABC.
改:若在Rt△ABC中,∠ACB=Rt∠,
CD⊥AB于D
且∠A=300
则△ACD∽△ABC?
△ACD与△CBD呢?
三个角对应相等,
三条边对应成比例的两个三角形,
叫做相似三角形(similar
trianglec).
△ABC与△DEF相似,
就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
性质:相似三角形的各对应角相等,各对应边对应成比例.
如果△
ABC∽
△DEF,
那么∠A
=
∠D,∠B
=
∠E,
∠C
=
∠F.
课堂小结
同课章节目录
