2020-2021学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览


文档简介
2020-2021学年浙教新版九年级上册数学《第4章
相似三角形》单元测试卷
一.选择题
1.点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A.
B.
C.
+1
D.﹣1
2.若两个相似五边形的相似比为3:5,则它们的面积比为( )
A.3:5
B.5:3
C.9:25
D.25:9
3.已知2x=3y,则下列比例式成立的是( )
A.
B.
C.
D.
4.如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
5.设a>0,b>0,称为a,b的“调和平均数”,如图,C为线段AB上的点,且AC=a,BC=b,O是AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,如:图中的线段OD的长度是a,b的算术平均数,则长度是a,b的“调和平均数”的线段是( )
A.OC
B.CE
C.DE
D.OE
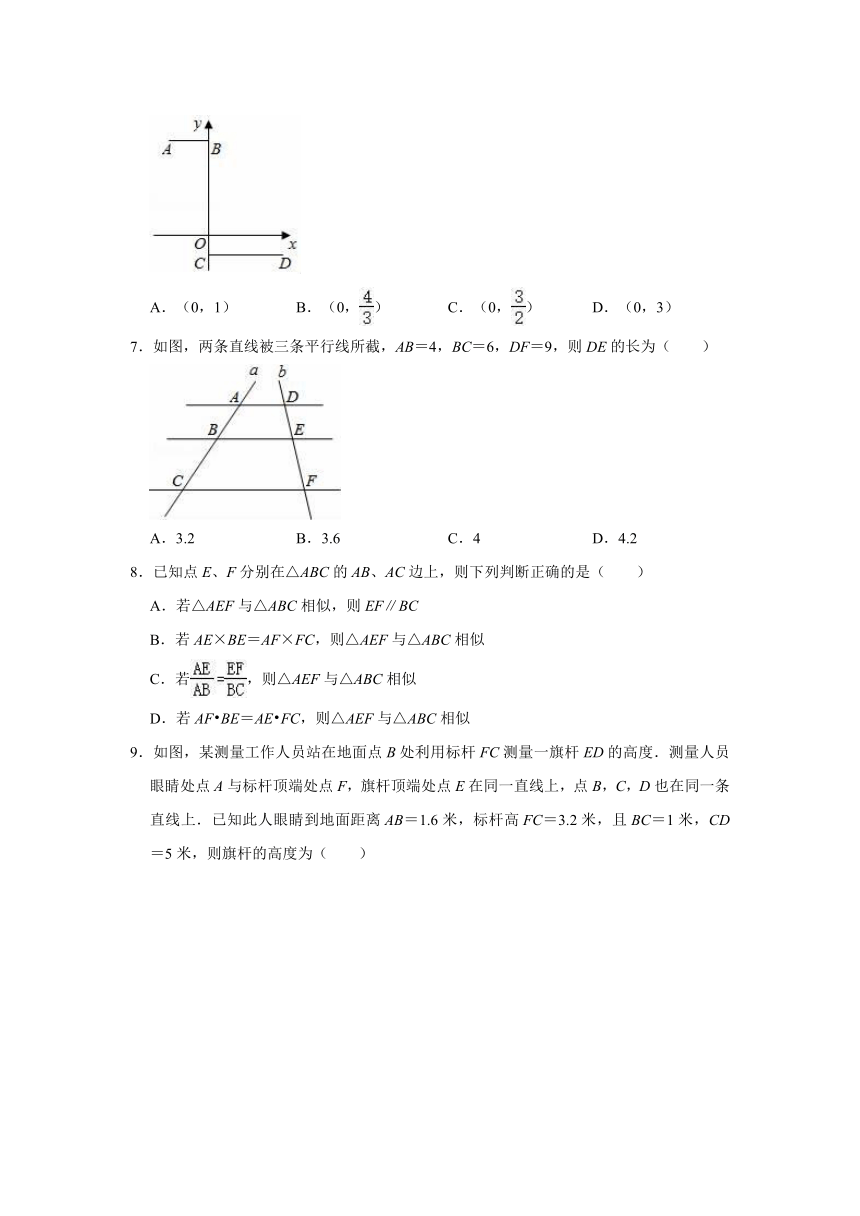
6.如图.在平面直角坐标系中,点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1).若线段AB和CD是位似图形,位似中心在y轴上,则位似中心的坐标为( )
A.(0,1)
B.(0,)
C.(0,)
D.(0,3)
7.如图,两条直线被三条平行线所截,AB=4,BC=6,DF=9,则DE的长为( )
A.3.2
B.3.6
C.4
D.4.2
8.已知点E、F分别在△ABC的AB、AC边上,则下列判断正确的是( )
A.若△AEF与△ABC相似,则EF∥BC
B.若AE×BE=AF×FC,则△AEF与△ABC相似
C.若,则△AEF与△ABC相似
D.若AF?BE=AE?FC,则△AEF与△ABC相似
9.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离AB=1.6米,标杆高FC=3.2米,且BC=1米,CD=5米,则旗杆的高度为( )
A.8.4米
B.9.6米
C.11.2米
D.12.4米
10.在坐标系中,已知A(6,0),B(0,8),C(0,﹣2),过点C作直线L交x轴于点D,使得以点D、C、O为顶点的三角形与△AOB相似,这样的直线一共可以作( )条.
A.3
B.4
C.5
D.6
二.填空题
11.两个三角形的相似比是2:3,那么它们面积的比是
.
12.已知3a﹣5b=0,则=
.
13.四条线段a、b、c、d成比例,其中a=3cm,b=9cm,d=6cm,则c=
.
14.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽,以AB为长的矩形面积为S2,S1
S2(填“>”或“=”或“<”).
15.若两个相似多边形的相似比是2:3,则它们的面积比等于
.
16.如图,周一某校升国旗时,甲、乙两名同学分别站在C、D的位置时,乙的影子AD刚好在甲的影子AC里边,已知甲身高BC为1.6米,乙身高DE为1.4米,甲的影长AC是6米,则甲、乙同学相距
米.
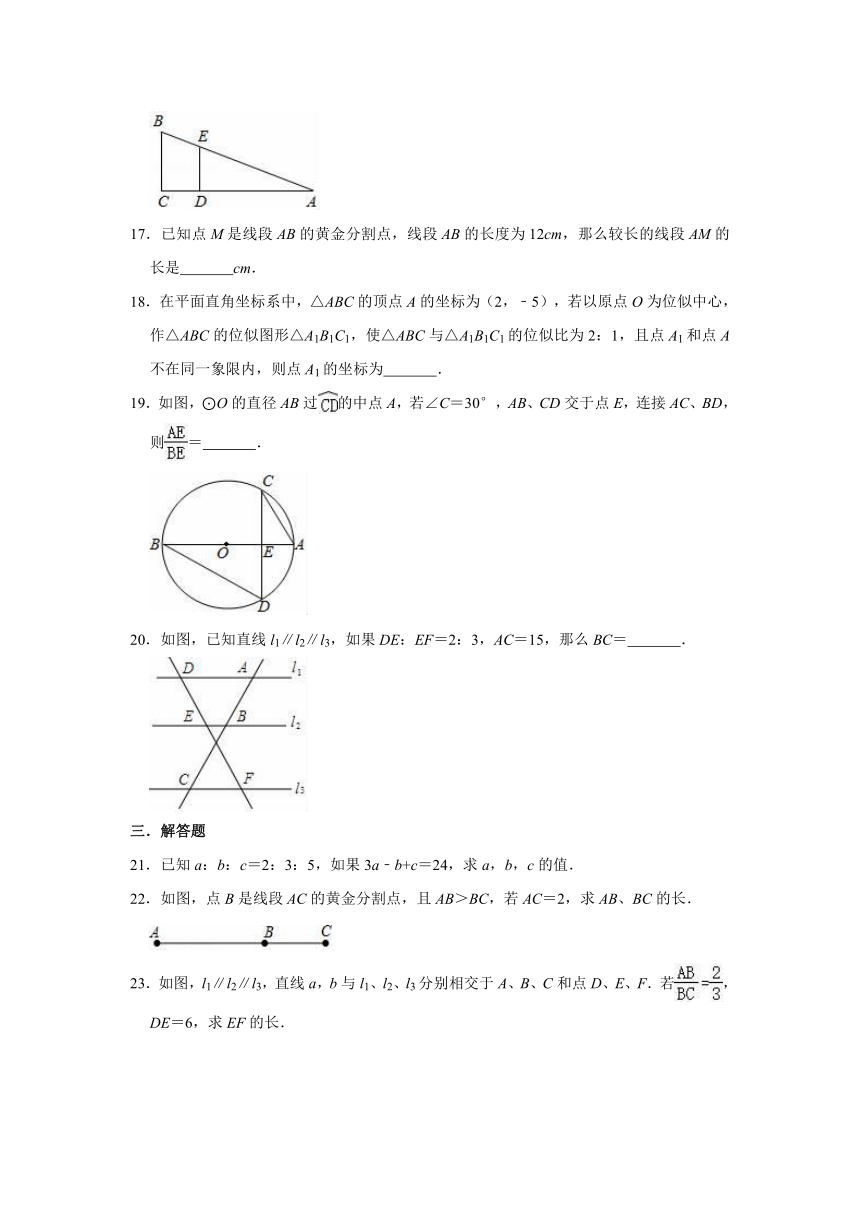
17.已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是
cm.
18.在平面直角坐标系中,△ABC的顶点A的坐标为(2,﹣5),若以原点O为位似中心,作△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为2:1,且点A1和点A不在同一象限内,则点A1的坐标为
.
19.如图,⊙O的直径AB过的中点A,若∠C=30°,AB、CD交于点E,连接AC、BD,则=
.
20.如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC=
.
三.解答题
21.已知a:b:c=2:3:5,如果3a﹣b+c=24,求a,b,c的值.
22.如图,点B是线段AC的黄金分割点,且AB>BC,若AC=2,求AB、BC的长.
23.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若,DE=6,求EF的长.
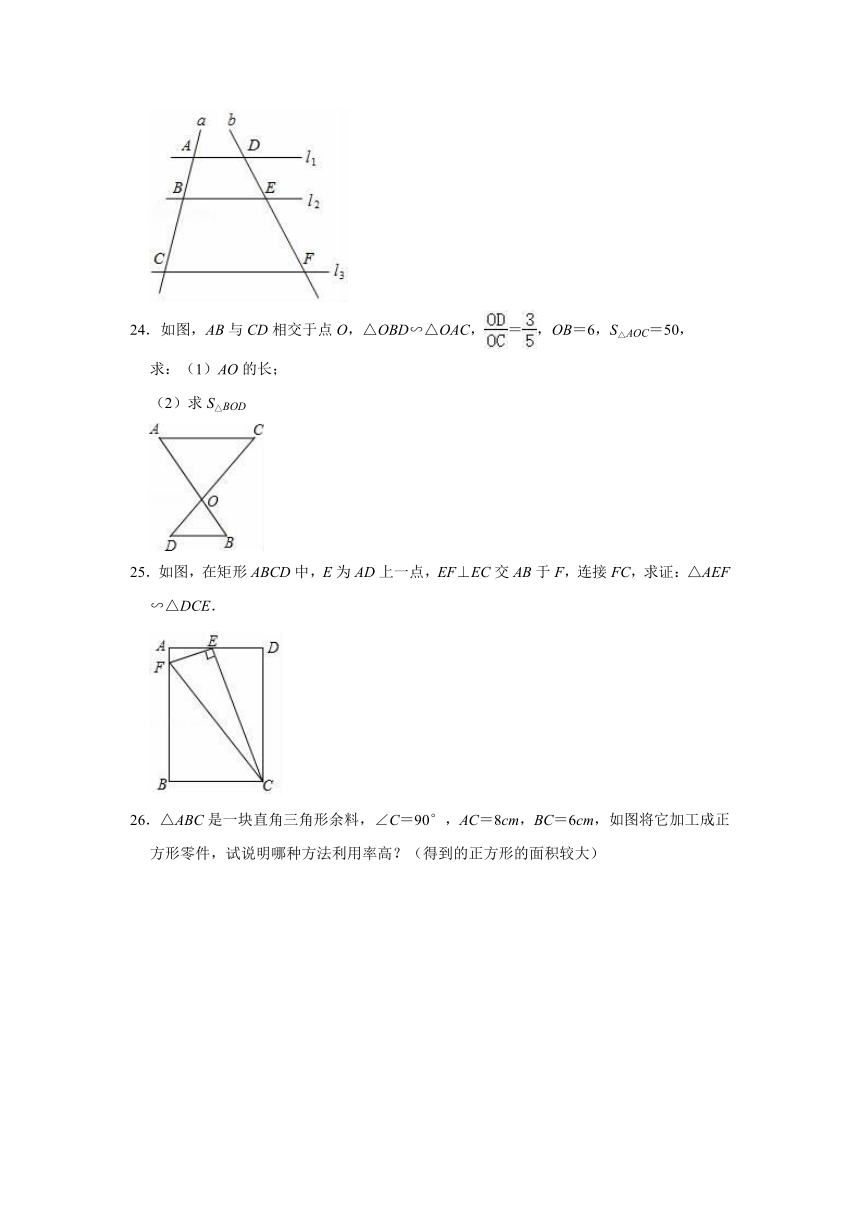
24.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=6,S△AOC=50,
求:(1)AO的长;
(2)求S△BOD
25.如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,求证:△AEF∽△DCE.
26.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
27.两个相似多边形的最长边分别为6cm和8cm,它们的周长之和为56cm,面积之差为28cm2,求较小相似多边形的周长与面积.
参考答案与试题解析
一.选择题
1.解:∵点B是线段AC的黄金分割点,且AB<BC,
∴BC=AC,
∵AC=2,
∴BC=﹣1.
故选:D.
2.解:∵两个相似五边形的相似比为3:5,
∴它们的面积比为:9:25.
故选:C.
3.解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:2x=﹣5y,故错误;
故选:C.
4.解:∵△ABO∽△CDO,
∴,
∵BO=8,DO=4,CD=3,
∴=,
解得:AB=6.
故选:D.
5.解:∵AB是圆的直径,
∴∠ADB=90°,又DC⊥AB,
∴CD2=AC?BC=ab,
∵线段OD的长度是a,b的算术平均数,
∴OD=,
∵DC⊥OC,CE⊥OD,
∴CD2=DE?OD,
∴DE===,
∴线段DE的长度是a,b的“调和平均数”,
故选:C.
6.解:连接AD交BC于E,则点E为位似中心,
∵点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1),
∴AB=2,CD=4,BC=6,
∵线段AB和CD是位似图形,
∴AB∥CD,
∴=,即=,
解得,BE=2,
∴OE=OB﹣BE=3,
∴位似中心点E的坐标为(0,3),
故选:D.
7.解:∵AD∥BE∥CF,
∴,
∴,
∵DF=9,
∴DE=,
故选:B.
8.解:选项A错误,∵△AEF与△ABC相似,可能是∠AEF=∠C,推不出EF∥BC.
选项B错误,由AE×BE=AF×FC,推不出△AEF与△ABC相似.
选项C错误,由,推不出△AEF与△ABC相似.
选项D正确.理由:∵AF?BE=AE?FC,
∴=,
∴EF∥BC,
∴△AEF∽△ABC.
故选:D.
9.解:作AH⊥ED交FC于点G,如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=3.2,BC=1,CD=5,
∴FG=3.2﹣1.6=1.6,BD=6,
∵FG∥EH,
∴,=
解得:EH=9.6,
∴ED=9.6+1.6=11.2(m)
答:电视塔的高ED是11.2米,
故选:C.
10.解:若△AOB∽△COD,则==,
∴OD=,则D(,0)或(﹣,0).
若△AOB∽△DOC,则==,
∴OD=,则D(,0)或(﹣,0).
所以可以作出四条直线.
故选:B.
二.填空题
11.解:∵两个三角形的相似比是2:3,
∴它们面积的比是()2=,
故答案为:4:9.
12.解:∵3a﹣5b=0,
∴3a=5b,
∴=;
故答案为:.
13.解:∵四条线段a、b、c、d成比例,
∴=,
∵a=3cm,b=9cm,d=6cm,
∴=,
解得:c=2(cm),
故答案为:2cm.
14.解:∵点P是线段AB的黄金分割点,且AP>BP,
∴AP2=BP×AB,
又∵S1=AP2,S2=PB×AB,
∴S1=S2.
故答案为:=.
15.解:∵两个相似多边形的相似比为2:3,
∴它们的面积比=22:32=4:9.
故答案为:4:9
16.解:设两个同学相距x米,
∵△ADE∽△ACB,
∴=,
∴=,
解得:CD=0.75.
故答案为0.75.
17.解:∵点M是线段AB的黄金分割点,AM>BM,
∴AM=AB=(6﹣6)厘米,
故答案为:(6﹣6).
18.解:在同一象限内,
∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),
∴则点A′的坐标为:(1,﹣2.5),
不在同一象限内,
∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),
∴则点A′的坐标为:(﹣1,2.5),
故答案为:(﹣1,2.5).
19.解:∵⊙O的直径AB过的中点A,
∴=,
∴DE=EC,
∵AB是⊙O的直径,
∴∠BED=∠CEA=90°,
∵∠C=30°,
∴∠DCA=∠DBA=30°,
∴△AEC∽△DEB,
∴=,
设DE=EC=x,
∵∠C=30°,
∴AE=x,
∵∠DBA=30°,
∴BE=x,
∴==;
故答案为:.
20.解:∵l1∥l2∥l3,
∴,
∴,
∵AC=15,
∴BC=9,
故答案为:9.
三.解答题
21.解:∵a:b:c=2:3:5,
∴设a=2t,b=3t,c=5t,
∵3a﹣b+c=24,
∴6t﹣3t+5t=24,解得t=3,
∴a=6,b=9,c=15.
22.解:∵点B是线段AC的黄金分割点,且AB>BC,
∴AB=×AC=﹣1,
∴BC=AC﹣AB=2﹣(﹣1)=3﹣.
23.解:∵l1∥l2∥l3,
∴,
∵,DE=6,
∴,
∴EF=9.
24.解:(1)∵△OBD∽△OAC,
∴==,
∵BO=6,
∴AO=10;
(2)∵△OBD∽△OAC,=,
∴=,
∵S△AOC=50,
∴S△BOD=18.
25.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵ABCD是矩形,
∴∠A=∠D=90°,
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE,
又∵∠A=∠D,
∴△AEF∽△DCE.
26.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB===10,
∵CH?AB=AC?BC
∴CH==(cm),
设正方形MNPQ边长为x,则QM=x,BJ=﹣x,
∵QM∥AB,
∴△CMQ∽△CBA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为(cm);
∵=>,
∴图1利用率高.
27.解:设较小相似多边形的周长为x,面积为y,则较大相似多边形的周长为56﹣x,面积28+y,
根据题意得=,=()2,
解得x=24,y=36,
所以较小相似多边形的周长为24cm,面积为36cm2.
相似三角形》单元测试卷
一.选择题
1.点B是线段AC的黄金分割点,且AB<BC,若AC=2,则BC的长为( )
A.
B.
C.
+1
D.﹣1
2.若两个相似五边形的相似比为3:5,则它们的面积比为( )
A.3:5
B.5:3
C.9:25
D.25:9
3.已知2x=3y,则下列比例式成立的是( )
A.
B.
C.
D.
4.如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
5.设a>0,b>0,称为a,b的“调和平均数”,如图,C为线段AB上的点,且AC=a,BC=b,O是AB的中点,以AB为直径作半圆,过点C作AB的垂线交半圆于D,连接OD,AD,BD,过点C作OD的垂线,垂足为E,如:图中的线段OD的长度是a,b的算术平均数,则长度是a,b的“调和平均数”的线段是( )
A.OC
B.CE
C.DE
D.OE
6.如图.在平面直角坐标系中,点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1).若线段AB和CD是位似图形,位似中心在y轴上,则位似中心的坐标为( )
A.(0,1)
B.(0,)
C.(0,)
D.(0,3)
7.如图,两条直线被三条平行线所截,AB=4,BC=6,DF=9,则DE的长为( )
A.3.2
B.3.6
C.4
D.4.2
8.已知点E、F分别在△ABC的AB、AC边上,则下列判断正确的是( )
A.若△AEF与△ABC相似,则EF∥BC
B.若AE×BE=AF×FC,则△AEF与△ABC相似
C.若,则△AEF与△ABC相似
D.若AF?BE=AE?FC,则△AEF与△ABC相似
9.如图,某测量工作人员站在地面点B处利用标杆FC测量一旗杆ED的高度.测量人员眼睛处点A与标杆顶端处点F,旗杆顶端处点E在同一直线上,点B,C,D也在同一条直线上.已知此人眼睛到地面距离AB=1.6米,标杆高FC=3.2米,且BC=1米,CD=5米,则旗杆的高度为( )
A.8.4米
B.9.6米
C.11.2米
D.12.4米
10.在坐标系中,已知A(6,0),B(0,8),C(0,﹣2),过点C作直线L交x轴于点D,使得以点D、C、O为顶点的三角形与△AOB相似,这样的直线一共可以作( )条.
A.3
B.4
C.5
D.6
二.填空题
11.两个三角形的相似比是2:3,那么它们面积的比是
.
12.已知3a﹣5b=0,则=
.
13.四条线段a、b、c、d成比例,其中a=3cm,b=9cm,d=6cm,则c=
.
14.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽,以AB为长的矩形面积为S2,S1
S2(填“>”或“=”或“<”).
15.若两个相似多边形的相似比是2:3,则它们的面积比等于
.
16.如图,周一某校升国旗时,甲、乙两名同学分别站在C、D的位置时,乙的影子AD刚好在甲的影子AC里边,已知甲身高BC为1.6米,乙身高DE为1.4米,甲的影长AC是6米,则甲、乙同学相距
米.
17.已知点M是线段AB的黄金分割点,线段AB的长度为12cm,那么较长的线段AM的长是
cm.
18.在平面直角坐标系中,△ABC的顶点A的坐标为(2,﹣5),若以原点O为位似中心,作△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的位似比为2:1,且点A1和点A不在同一象限内,则点A1的坐标为
.
19.如图,⊙O的直径AB过的中点A,若∠C=30°,AB、CD交于点E,连接AC、BD,则=
.
20.如图,已知直线l1∥l2∥l3,如果DE:EF=2:3,AC=15,那么BC=
.
三.解答题
21.已知a:b:c=2:3:5,如果3a﹣b+c=24,求a,b,c的值.
22.如图,点B是线段AC的黄金分割点,且AB>BC,若AC=2,求AB、BC的长.
23.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若,DE=6,求EF的长.
24.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=6,S△AOC=50,
求:(1)AO的长;
(2)求S△BOD
25.如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,求证:△AEF∽△DCE.
26.△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
27.两个相似多边形的最长边分别为6cm和8cm,它们的周长之和为56cm,面积之差为28cm2,求较小相似多边形的周长与面积.
参考答案与试题解析
一.选择题
1.解:∵点B是线段AC的黄金分割点,且AB<BC,
∴BC=AC,
∵AC=2,
∴BC=﹣1.
故选:D.
2.解:∵两个相似五边形的相似比为3:5,
∴它们的面积比为:9:25.
故选:C.
3.解:A、变成等积式是:xy=6,故错误;
B、变成等积式是:3x=y,故错误;
C、变成等积式是:2x=3y,故正确;
D、变成等积式是:2x=﹣5y,故错误;
故选:C.
4.解:∵△ABO∽△CDO,
∴,
∵BO=8,DO=4,CD=3,
∴=,
解得:AB=6.
故选:D.
5.解:∵AB是圆的直径,
∴∠ADB=90°,又DC⊥AB,
∴CD2=AC?BC=ab,
∵线段OD的长度是a,b的算术平均数,
∴OD=,
∵DC⊥OC,CE⊥OD,
∴CD2=DE?OD,
∴DE===,
∴线段DE的长度是a,b的“调和平均数”,
故选:C.
6.解:连接AD交BC于E,则点E为位似中心,
∵点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1),
∴AB=2,CD=4,BC=6,
∵线段AB和CD是位似图形,
∴AB∥CD,
∴=,即=,
解得,BE=2,
∴OE=OB﹣BE=3,
∴位似中心点E的坐标为(0,3),
故选:D.
7.解:∵AD∥BE∥CF,
∴,
∴,
∵DF=9,
∴DE=,
故选:B.
8.解:选项A错误,∵△AEF与△ABC相似,可能是∠AEF=∠C,推不出EF∥BC.
选项B错误,由AE×BE=AF×FC,推不出△AEF与△ABC相似.
选项C错误,由,推不出△AEF与△ABC相似.
选项D正确.理由:∵AF?BE=AE?FC,
∴=,
∴EF∥BC,
∴△AEF∽△ABC.
故选:D.
9.解:作AH⊥ED交FC于点G,如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=3.2,BC=1,CD=5,
∴FG=3.2﹣1.6=1.6,BD=6,
∵FG∥EH,
∴,=
解得:EH=9.6,
∴ED=9.6+1.6=11.2(m)
答:电视塔的高ED是11.2米,
故选:C.
10.解:若△AOB∽△COD,则==,
∴OD=,则D(,0)或(﹣,0).
若△AOB∽△DOC,则==,
∴OD=,则D(,0)或(﹣,0).
所以可以作出四条直线.
故选:B.
二.填空题
11.解:∵两个三角形的相似比是2:3,
∴它们面积的比是()2=,
故答案为:4:9.
12.解:∵3a﹣5b=0,
∴3a=5b,
∴=;
故答案为:.
13.解:∵四条线段a、b、c、d成比例,
∴=,
∵a=3cm,b=9cm,d=6cm,
∴=,
解得:c=2(cm),
故答案为:2cm.
14.解:∵点P是线段AB的黄金分割点,且AP>BP,
∴AP2=BP×AB,
又∵S1=AP2,S2=PB×AB,
∴S1=S2.
故答案为:=.
15.解:∵两个相似多边形的相似比为2:3,
∴它们的面积比=22:32=4:9.
故答案为:4:9
16.解:设两个同学相距x米,
∵△ADE∽△ACB,
∴=,
∴=,
解得:CD=0.75.
故答案为0.75.
17.解:∵点M是线段AB的黄金分割点,AM>BM,
∴AM=AB=(6﹣6)厘米,
故答案为:(6﹣6).
18.解:在同一象限内,
∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),
∴则点A′的坐标为:(1,﹣2.5),
不在同一象限内,
∵△ABC与△A′B′C′是以原点O为位似中心的位似图形,其中相似比是2:1,A坐标为(2,﹣5),
∴则点A′的坐标为:(﹣1,2.5),
故答案为:(﹣1,2.5).
19.解:∵⊙O的直径AB过的中点A,
∴=,
∴DE=EC,
∵AB是⊙O的直径,
∴∠BED=∠CEA=90°,
∵∠C=30°,
∴∠DCA=∠DBA=30°,
∴△AEC∽△DEB,
∴=,
设DE=EC=x,
∵∠C=30°,
∴AE=x,
∵∠DBA=30°,
∴BE=x,
∴==;
故答案为:.
20.解:∵l1∥l2∥l3,
∴,
∴,
∵AC=15,
∴BC=9,
故答案为:9.
三.解答题
21.解:∵a:b:c=2:3:5,
∴设a=2t,b=3t,c=5t,
∵3a﹣b+c=24,
∴6t﹣3t+5t=24,解得t=3,
∴a=6,b=9,c=15.
22.解:∵点B是线段AC的黄金分割点,且AB>BC,
∴AB=×AC=﹣1,
∴BC=AC﹣AB=2﹣(﹣1)=3﹣.
23.解:∵l1∥l2∥l3,
∴,
∵,DE=6,
∴,
∴EF=9.
24.解:(1)∵△OBD∽△OAC,
∴==,
∵BO=6,
∴AO=10;
(2)∵△OBD∽△OAC,=,
∴=,
∵S△AOC=50,
∴S△BOD=18.
25.证明:∵∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵ABCD是矩形,
∴∠A=∠D=90°,
∵∠A+∠AFE+∠AEF=180°,
∴∠AFE+∠AEF=90°,
∴∠DEC=∠AFE,
又∵∠A=∠D,
∴△AEF∽△DCE.
26.解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB===10,
∵CH?AB=AC?BC
∴CH==(cm),
设正方形MNPQ边长为x,则QM=x,BJ=﹣x,
∵QM∥AB,
∴△CMQ∽△CBA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为(cm);
∵=>,
∴图1利用率高.
27.解:设较小相似多边形的周长为x,面积为y,则较大相似多边形的周长为56﹣x,面积28+y,
根据题意得=,=()2,
解得x=24,y=36,
所以较小相似多边形的周长为24cm,面积为36cm2.
同课章节目录
