2020-2021学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 00:00:00 | ||
图片预览


文档简介
2020-2021学年浙教新版八年级上册数学《第1章
三角形的初步认识》单元测试卷
一.选择题
1.等边三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰直角三角形
2.如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为( )
A.2
B.3
C.4
D.5
3.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4
B.4.5
C.3.5
D.5
4.下列命题中:①带根号的数是无理数;②如果a<0,b>0,那么a+b<0;③平面内的三条直线a,b,c,若a∥b,b∥c,则a∥c;④平面内的三条直线a,b,c,若a⊥b,b⊥c,则a⊥c.真命题的个数是( )
A.1
B.2
C.3
D.4
5.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.30°
B.35°
C.25°
D.20°
6.在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A.
B.
C.
D.
7.如图,已知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
A.BC=AD
B.∠B=∠D=90°
C.∠BAC=∠DCA
D.∠ACB=∠CAD
8.老师让4个学生猜一猜这次考试中4个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗?( )
A.甲
B.乙
C.丙
D.丁
9.具备下列条件的△ABC,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=∠B=∠C
C.∠A=2∠B=3∠C
D.∠A:∠B:∠C=1:3:4
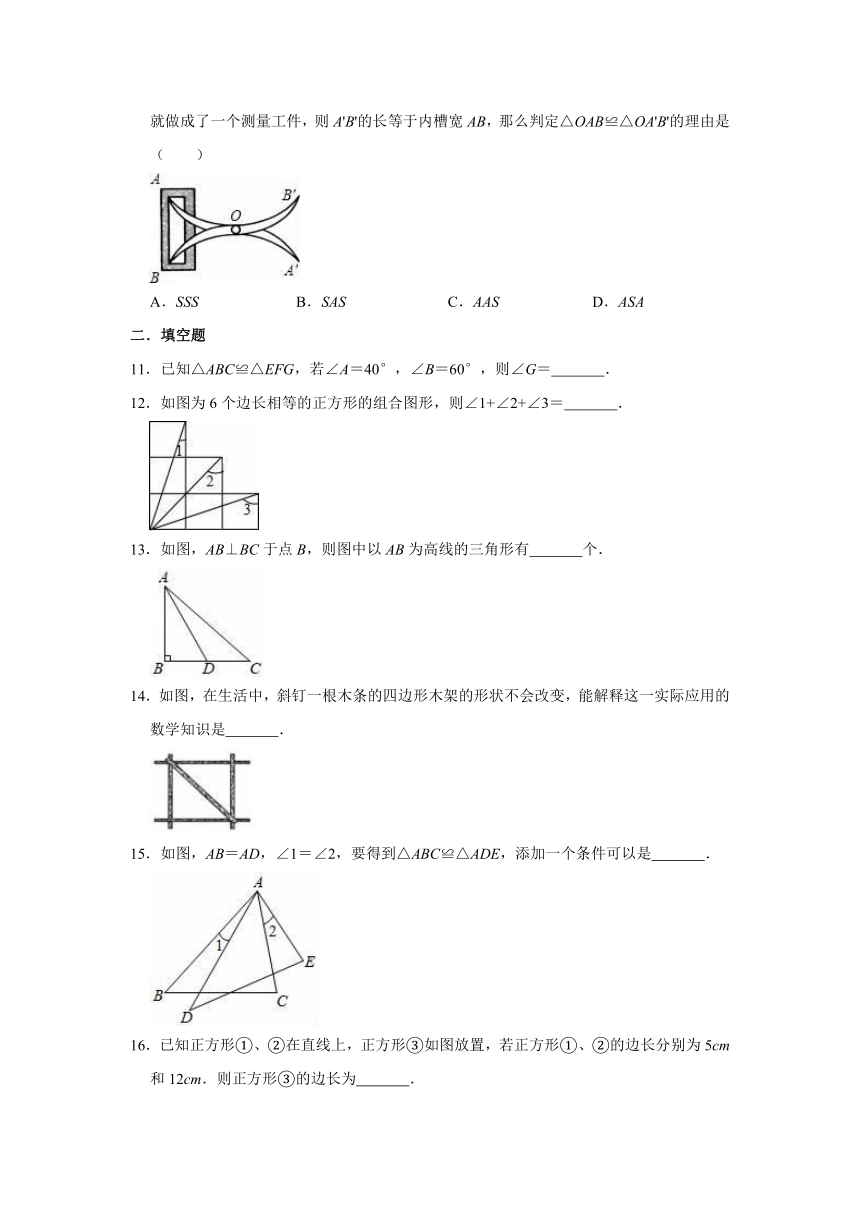
10.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是( )
A.SSS
B.SAS
C.AAS
D.ASA
二.填空题
11.已知△ABC≌△EFG,若∠A=40°,∠B=60°,则∠G=
.
12.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=
.
13.如图,AB⊥BC于点B,则图中以AB为高线的三角形有
个.
14.如图,在生活中,斜钉一根木条的四边形木架的形状不会改变,能解释这一实际应用的数学知识是
.
15.如图,AB=AD,∠1=∠2,要得到△ABC≌△ADE,添加一个条件可以是
.
16.已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的边长分别为5cm和12cm.则正方形③的边长为
.
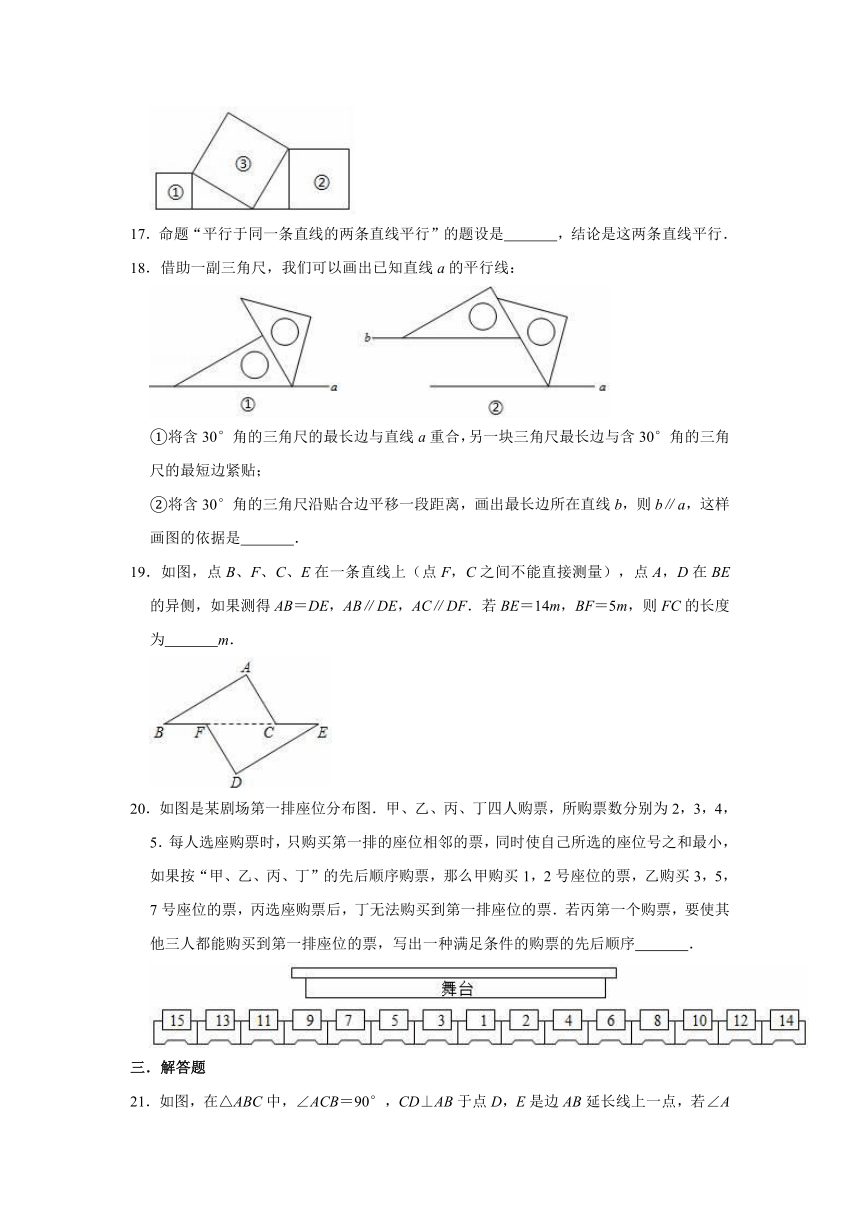
17.命题“平行于同一条直线的两条直线平行”的题设是
,结论是这两条直线平行.
18.借助一副三角尺,我们可以画出已知直线a的平行线:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a,这样画图的依据是
.
19.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
20.如图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小,如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序
.
三.解答题
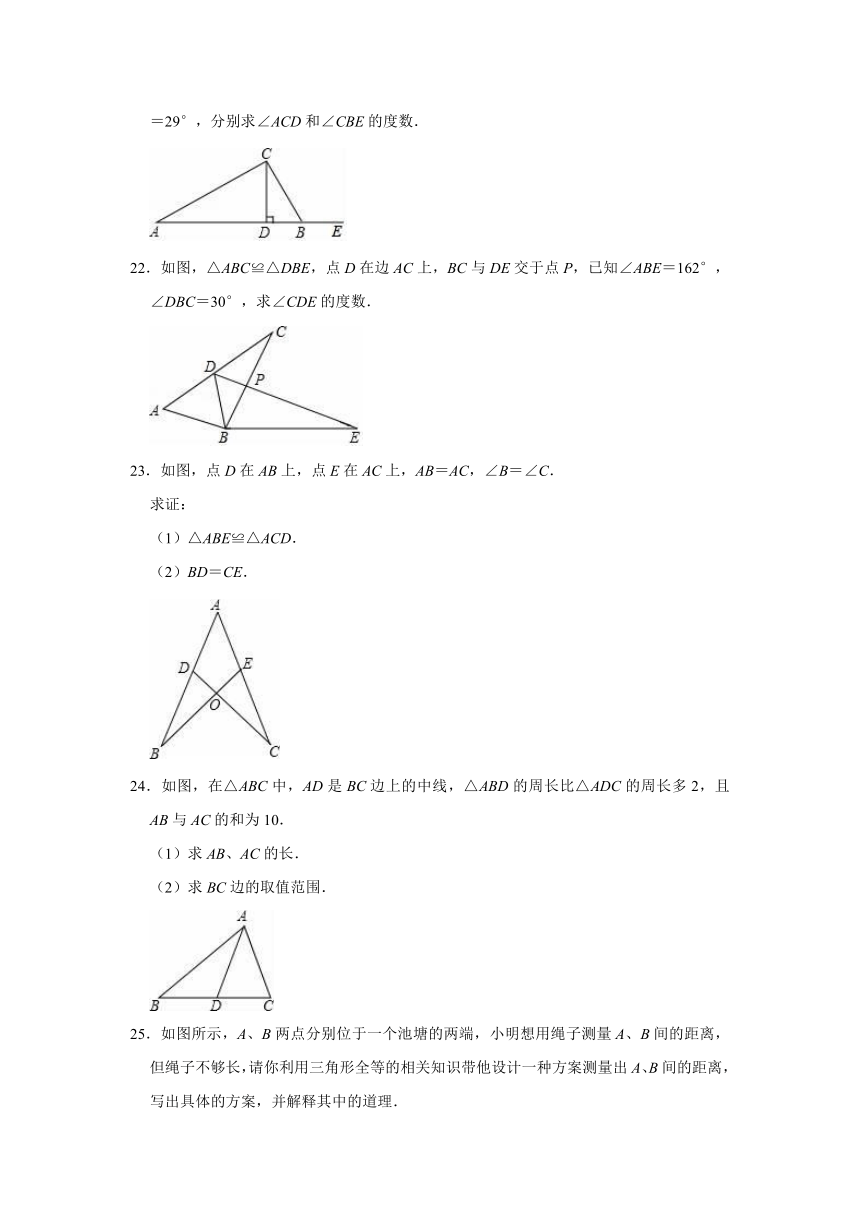
21.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,E是边AB延长线上一点,若∠A=29°,分别求∠ACD和∠CBE的度数.
22.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
23.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:
(1)△ABE≌△ACD.
(2)BD=CE.
24.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
25.如图所示,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,请你利用三角形全等的相关知识带他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理.
26.用1,2,3三个数字组成六位数,若每个数字用两次,相邻位不允许用相同的数字.
(1)试写出四个符合上述条件的六位数;
(2)请你计算出符合上述条件的六位数共有多少个?
27.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①画一个面积为10的正方形;
(2)在图②画一个面积为12的菱形.
参考答案与试题解析
一.选择题
1.解:等边三角形的三个内角都是60度,属于锐角三角形;等边三角形的三条边都相等,属于等腰三角形.观察选项,选项B符合题意.
故选:B.
2.解:∵△ABC的面积为12,
∴×AE×BC=12,
∴BC==6,
∵AD是边BC上的中线,
∴CD=BC=3.
故选:B.
3.解:∵△ABC的中线AD、BE相交于点F,
∴BD=CD,点F为△ABC的重心,
∴BF=2EF,AF=2FD,
∴S△BFD=S△ABF=×4=2,S△AEF=S△ABF=×4=2,
∵S△ABD=S△ACD=4+2=6,
∴四边形FDCE的面积=6﹣2=4.
故选:A.
4.解:①=2,是有理数,则带根号的数是无理数是假命题;
②如果a<0,b>0,|a|>|b|,那么a+b<0,本小题说法是假命题;
③平面内的三条直线a,b,c,若a∥b,b∥c,则a∥c,本小题说法是真命题;
④平面内的三条直线a,b,c,若a⊥b,b⊥c,则a∥c,本小题说法是假命题;
故选:A.
5.解:在△DOC中,∠D=80°,∠DOC=70°,
∴∠C=180°﹣80°﹣70°=30°,
∵△ABO≌△DCO,
∴∠B=∠C=30°,
故选:A.
6.解:∵∠ADC=∠B+∠BCD,∠ADC=2∠B,
∴∠B=∠BCD,
∴DB=DC,
∴点D为BC的垂直平分线与AB的交点.
故选:C.
7.解:A、在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),正确,故本选项不符合题意;
B、∵∠B=∠D=90°,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),正确,故本选项不符合题意;
C、在△ABC和△CDA中,
,
∴△ABC≌△CDA(SAS),正确,故本选项不符合题意;
D、根据AB=CD,AC=CA,∠ACB=∠CAD不能推出△ABC≌△CDA,错误,故本选项符合题意;
故选:D.
8.解:假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好,
故选:C.
9.解:A、由∠A+∠B=∠C,可以推出∠C=90°,本选项不符合题意.
B、由∠A=∠B=∠C,可以推出∠C=90°,本选项不符合题意.
C、由∠A=2∠B=3∠C,推出∠A=()°,△ABC是钝角三角形,本选项符合题意.
D、由∠A:∠B:∠C=1:3:4,可以推出∠C=90°,本选项不符合题意,
故选:C.
10.解:△OAB与△OA′B′中,
∵AO=A′O,∠AOB=∠A′OB′,BO=B′O,
∴△OAB≌△OA′B′(SAS).
故选:B.
二.填空题
11.解:在△ABC中,∠A=40°,∠B=60°,
∴∠C=180°﹣∠A=∠B=80°,
∵△ABC≌△EFG,
∴∠G=∠C=80°,
故答案为:80°.
12.解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
13.解:图中以AB为高线的三角形有△ACB,△ADC,△ADB,共3个,
故答案为:3.
14.解:斜钉一根木条的四边形木架的形状不会改变,能解释这一实际应用的数学知识是三角形具有稳定性,
故答案为:三角形具有稳定性.
15.解:∵∠1=∠2,
∴∠BAC=∠DAE,
且AB=AD,故再加一组边即AC=AE,或再加一组角即∠B=∠D,或∠C=∠E,
故答案为:∠B=∠D(或者∠C=∠E,AC=AE).
16.解:如图,
∵四边形①、②、③都是正方形,
∴∠EAB=∠EBD=∠BCD=90°,BE=BD,
∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,
∴∠AEB=∠CBD,
在△ABE和△CDB中,
,
∴△ABE≌△CDB(AAS),
∴CD=AB=12(cm),
∴BE===13(cm),
故答案为:13cm.
17.解:题设为:两条直线平行于同一条直线,结论为:这两条直线平行,
故答案为:两条直线平行于同一条直线.
18.解:如图2中,由作图可知,∠1=∠2=60°,
∴a∥b(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行.
19.解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC﹣FC=EF﹣FC,
即BF=CE=5m,
∴FC=BE﹣BF﹣CE=14m﹣5m﹣5m=4m;
故答案为:4.
20.解:根据题意,丙第一个购票,只能购买3,1,2,4号票,
此时,3号左边有6个座位,4号右边有5个座位,
即甲、乙购买的票只要在丙的同侧,四个人购买的票全在第一排,
①第二个丁可以购买3号左边的5个座位,另一侧的座位甲和乙购买,
即丙(3,1,2,4)、丁(5,7,9,11,13)、甲(6,8)、乙(10,12,14),
或丙(3,1,2,4)、丁(5,7,9,11,13)、乙(6,8,10)、甲(12,14);
②第二个由甲或乙购买,此时,只能购买5,7号票,第三个购买的只能是丁,且只能购买6,8,10,12,14号票,
此时,四个人购买的票全在第一排,
即丙(3,1,2,4)、甲(5,7)、丁(6,8,10,12,14)、乙(9,11,13),
或丙(3,1,2,4)、乙(5,7,9)、丁(6,8,10,12,14)、甲(11,13),
因此,第一个是丙购买票,丁只要不是最后一个购买票的人,都能使四个人购买的票全在第一排,
故答案为:丙、丁、甲、乙.
三.解答题
21.解:∵CD⊥AB,
∴∠ADC=90°,
又∵∠A=29°,
∴∠ACD=90°﹣∠A=90°﹣29°=61°,
∵∠CBE是△ABC的外角,∠ACB=90°,
∴∠CBE=∠A+∠ACB=29°+90°=119°.
22.解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
23.证明:(1)在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA);
(2)∵△ABE≌△ACD,
∴AE=AD,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
24.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
25.解:如图,先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A、B间的距离.
证明:由题意知AC=DC,BC=EC,且∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB.
∴量出DE的长,就是A、B两点间的距离.
26.解:(1)以1开头的数有121323
131232
123123
123132
132123
132132
123213
132312
132321
123231
等10个数;
(2)121323,131232,123123,123132,121323,121332,132123,132132,123213,132312,213123,213132,312123,312132,212313,213213,312312,313212,213231,312321,231213,231312,321213,321312,231231,231321,321231,321321,232131,323121则共30个符合条件的六位数.
27.解:(1)如图①中,正方形ABCD即为所求.
(2)如图②中,菱形ABCD即为所求.
三角形的初步认识》单元测试卷
一.选择题
1.等边三角形是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰直角三角形
2.如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为( )
A.2
B.3
C.4
D.5
3.如图,△ABC的中线AD、BE相交于点F,若△ABF的面积是4,则四边形FDCE的面积是( )
A.4
B.4.5
C.3.5
D.5
4.下列命题中:①带根号的数是无理数;②如果a<0,b>0,那么a+b<0;③平面内的三条直线a,b,c,若a∥b,b∥c,则a∥c;④平面内的三条直线a,b,c,若a⊥b,b⊥c,则a⊥c.真命题的个数是( )
A.1
B.2
C.3
D.4
5.如图,△ABO≌△DCO,∠D=80°,∠DOC=70°,则∠B=( )
A.30°
B.35°
C.25°
D.20°
6.在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A.
B.
C.
D.
7.如图,已知AB=CD,从下列条件中补充一个条件后,仍不能判定△ABC≌△CDA的是( )
A.BC=AD
B.∠B=∠D=90°
C.∠BAC=∠DCA
D.∠ACB=∠CAD
8.老师让4个学生猜一猜这次考试中4个人的成绩谁最好.甲说:“乙最好”:乙说:“丁最好”;丙说:“反正我不是最好”;丁说:“乙说我最好,肯定错了”.老师告诉他们,只有一个人猜对了,于是,聪明的孩子们马上知道是谁的成绩最好了,你知道吗?( )
A.甲
B.乙
C.丙
D.丁
9.具备下列条件的△ABC,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=∠B=∠C
C.∠A=2∠B=3∠C
D.∠A:∠B:∠C=1:3:4
10.如图,将两根钢条AA'、BB'的中点O连在一起,使AA'、BB'可以绕着点O自由旋转,就做成了一个测量工件,则A'B'的长等于内槽宽AB,那么判定△OAB≌△OA'B'的理由是( )
A.SSS
B.SAS
C.AAS
D.ASA
二.填空题
11.已知△ABC≌△EFG,若∠A=40°,∠B=60°,则∠G=
.
12.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=
.
13.如图,AB⊥BC于点B,则图中以AB为高线的三角形有
个.
14.如图,在生活中,斜钉一根木条的四边形木架的形状不会改变,能解释这一实际应用的数学知识是
.
15.如图,AB=AD,∠1=∠2,要得到△ABC≌△ADE,添加一个条件可以是
.
16.已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的边长分别为5cm和12cm.则正方形③的边长为
.
17.命题“平行于同一条直线的两条直线平行”的题设是
,结论是这两条直线平行.
18.借助一副三角尺,我们可以画出已知直线a的平行线:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a,这样画图的依据是
.
19.如图,点B、F、C、E在一条直线上(点F,C之间不能直接测量),点A,D在BE的异侧,如果测得AB=DE,AB∥DE,AC∥DF.若BE=14m,BF=5m,则FC的长度为
m.
20.如图是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位号之和最小,如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一个购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序
.
三.解答题
21.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,E是边AB延长线上一点,若∠A=29°,分别求∠ACD和∠CBE的度数.
22.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
23.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:
(1)△ABE≌△ACD.
(2)BD=CE.
24.如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
25.如图所示,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,请你利用三角形全等的相关知识带他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理.
26.用1,2,3三个数字组成六位数,若每个数字用两次,相邻位不允许用相同的数字.
(1)试写出四个符合上述条件的六位数;
(2)请你计算出符合上述条件的六位数共有多少个?
27.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①画一个面积为10的正方形;
(2)在图②画一个面积为12的菱形.
参考答案与试题解析
一.选择题
1.解:等边三角形的三个内角都是60度,属于锐角三角形;等边三角形的三条边都相等,属于等腰三角形.观察选项,选项B符合题意.
故选:B.
2.解:∵△ABC的面积为12,
∴×AE×BC=12,
∴BC==6,
∵AD是边BC上的中线,
∴CD=BC=3.
故选:B.
3.解:∵△ABC的中线AD、BE相交于点F,
∴BD=CD,点F为△ABC的重心,
∴BF=2EF,AF=2FD,
∴S△BFD=S△ABF=×4=2,S△AEF=S△ABF=×4=2,
∵S△ABD=S△ACD=4+2=6,
∴四边形FDCE的面积=6﹣2=4.
故选:A.
4.解:①=2,是有理数,则带根号的数是无理数是假命题;
②如果a<0,b>0,|a|>|b|,那么a+b<0,本小题说法是假命题;
③平面内的三条直线a,b,c,若a∥b,b∥c,则a∥c,本小题说法是真命题;
④平面内的三条直线a,b,c,若a⊥b,b⊥c,则a∥c,本小题说法是假命题;
故选:A.
5.解:在△DOC中,∠D=80°,∠DOC=70°,
∴∠C=180°﹣80°﹣70°=30°,
∵△ABO≌△DCO,
∴∠B=∠C=30°,
故选:A.
6.解:∵∠ADC=∠B+∠BCD,∠ADC=2∠B,
∴∠B=∠BCD,
∴DB=DC,
∴点D为BC的垂直平分线与AB的交点.
故选:C.
7.解:A、在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS),正确,故本选项不符合题意;
B、∵∠B=∠D=90°,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),正确,故本选项不符合题意;
C、在△ABC和△CDA中,
,
∴△ABC≌△CDA(SAS),正确,故本选项不符合题意;
D、根据AB=CD,AC=CA,∠ACB=∠CAD不能推出△ABC≌△CDA,错误,故本选项符合题意;
故选:D.
8.解:假设甲最好,则甲说得错了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是甲最好;
假设乙最好,则甲说对了,则乙说错了,丙说对了,丁说对了,与老师说的“只有一个人猜对了,”矛盾,因此不是乙最好;
假设丙最好,则甲说错了,则乙说错了,丙说错了,丁说对了,与老师说的“只有一个人猜对了,”不矛盾,因此是丙最好;
假设丁最好,则甲说错了,则乙说对了,丙说对了,丁说错了,与老师说的“只有一个人猜对了,”矛盾,因此是丁不是最好;
因此丙的成绩最好,
故选:C.
9.解:A、由∠A+∠B=∠C,可以推出∠C=90°,本选项不符合题意.
B、由∠A=∠B=∠C,可以推出∠C=90°,本选项不符合题意.
C、由∠A=2∠B=3∠C,推出∠A=()°,△ABC是钝角三角形,本选项符合题意.
D、由∠A:∠B:∠C=1:3:4,可以推出∠C=90°,本选项不符合题意,
故选:C.
10.解:△OAB与△OA′B′中,
∵AO=A′O,∠AOB=∠A′OB′,BO=B′O,
∴△OAB≌△OA′B′(SAS).
故选:B.
二.填空题
11.解:在△ABC中,∠A=40°,∠B=60°,
∴∠C=180°﹣∠A=∠B=80°,
∵△ABC≌△EFG,
∴∠G=∠C=80°,
故答案为:80°.
12.解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∴∠1+∠2+∠3=90°+45°=135°,
故答案为:135°.
13.解:图中以AB为高线的三角形有△ACB,△ADC,△ADB,共3个,
故答案为:3.
14.解:斜钉一根木条的四边形木架的形状不会改变,能解释这一实际应用的数学知识是三角形具有稳定性,
故答案为:三角形具有稳定性.
15.解:∵∠1=∠2,
∴∠BAC=∠DAE,
且AB=AD,故再加一组边即AC=AE,或再加一组角即∠B=∠D,或∠C=∠E,
故答案为:∠B=∠D(或者∠C=∠E,AC=AE).
16.解:如图,
∵四边形①、②、③都是正方形,
∴∠EAB=∠EBD=∠BCD=90°,BE=BD,
∴∠AEB+∠ABE=90°,∠ABE+∠DBC=90°,
∴∠AEB=∠CBD,
在△ABE和△CDB中,
,
∴△ABE≌△CDB(AAS),
∴CD=AB=12(cm),
∴BE===13(cm),
故答案为:13cm.
17.解:题设为:两条直线平行于同一条直线,结论为:这两条直线平行,
故答案为:两条直线平行于同一条直线.
18.解:如图2中,由作图可知,∠1=∠2=60°,
∴a∥b(同位角相等,两直线平行).
故答案为:同位角相等,两直线平行.
19.解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
在△ABC和△DEF中,,
∴△ABC≌△DEF(AAS),
∴BC=EF,
∴BC﹣FC=EF﹣FC,
即BF=CE=5m,
∴FC=BE﹣BF﹣CE=14m﹣5m﹣5m=4m;
故答案为:4.
20.解:根据题意,丙第一个购票,只能购买3,1,2,4号票,
此时,3号左边有6个座位,4号右边有5个座位,
即甲、乙购买的票只要在丙的同侧,四个人购买的票全在第一排,
①第二个丁可以购买3号左边的5个座位,另一侧的座位甲和乙购买,
即丙(3,1,2,4)、丁(5,7,9,11,13)、甲(6,8)、乙(10,12,14),
或丙(3,1,2,4)、丁(5,7,9,11,13)、乙(6,8,10)、甲(12,14);
②第二个由甲或乙购买,此时,只能购买5,7号票,第三个购买的只能是丁,且只能购买6,8,10,12,14号票,
此时,四个人购买的票全在第一排,
即丙(3,1,2,4)、甲(5,7)、丁(6,8,10,12,14)、乙(9,11,13),
或丙(3,1,2,4)、乙(5,7,9)、丁(6,8,10,12,14)、甲(11,13),
因此,第一个是丙购买票,丁只要不是最后一个购买票的人,都能使四个人购买的票全在第一排,
故答案为:丙、丁、甲、乙.
三.解答题
21.解:∵CD⊥AB,
∴∠ADC=90°,
又∵∠A=29°,
∴∠ACD=90°﹣∠A=90°﹣29°=61°,
∵∠CBE是△ABC的外角,∠ACB=90°,
∴∠CBE=∠A+∠ACB=29°+90°=119°.
22.解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
23.证明:(1)在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA);
(2)∵△ABE≌△ACD,
∴AE=AD,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
24.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
25.解:如图,先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A、B间的距离.
证明:由题意知AC=DC,BC=EC,且∠ACB=∠DCE,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴DE=AB.
∴量出DE的长,就是A、B两点间的距离.
26.解:(1)以1开头的数有121323
131232
123123
123132
132123
132132
123213
132312
132321
123231
等10个数;
(2)121323,131232,123123,123132,121323,121332,132123,132132,123213,132312,213123,213132,312123,312132,212313,213213,312312,313212,213231,312321,231213,231312,321213,321312,231231,231321,321231,321321,232131,323121则共30个符合条件的六位数.
27.解:(1)如图①中,正方形ABCD即为所求.
(2)如图②中,菱形ABCD即为所求.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
