2020-2021学年浙教新版八年级上册数学《第5章 一次函数》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年浙教新版八年级上册数学《第5章 一次函数》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-22 22:12:39 | ||
图片预览



文档简介
2020-2021学年浙教新版八年级上册数学《第5章
一次函数》单元测试卷
一.选择题
1.小丽的微信红包原有100元钱,她在新年一周里抢红包,红包里的钱随着时间的变化而变化,在上述过程中,自变量是( )
A.时间
B.小丽
C.80元
D.红包里的钱
2.下列函数中:①y=﹣x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1
B.2
C.3
D.4
3.已知一辆汽车行驶的速度为50km/h,它行驶的路程s(单位:千米)与行驶的时间t(单位:小时)之间的关系是s=50t,其中常量是( )
A.s
B.50
C.t
D.s和t
4.函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
5.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
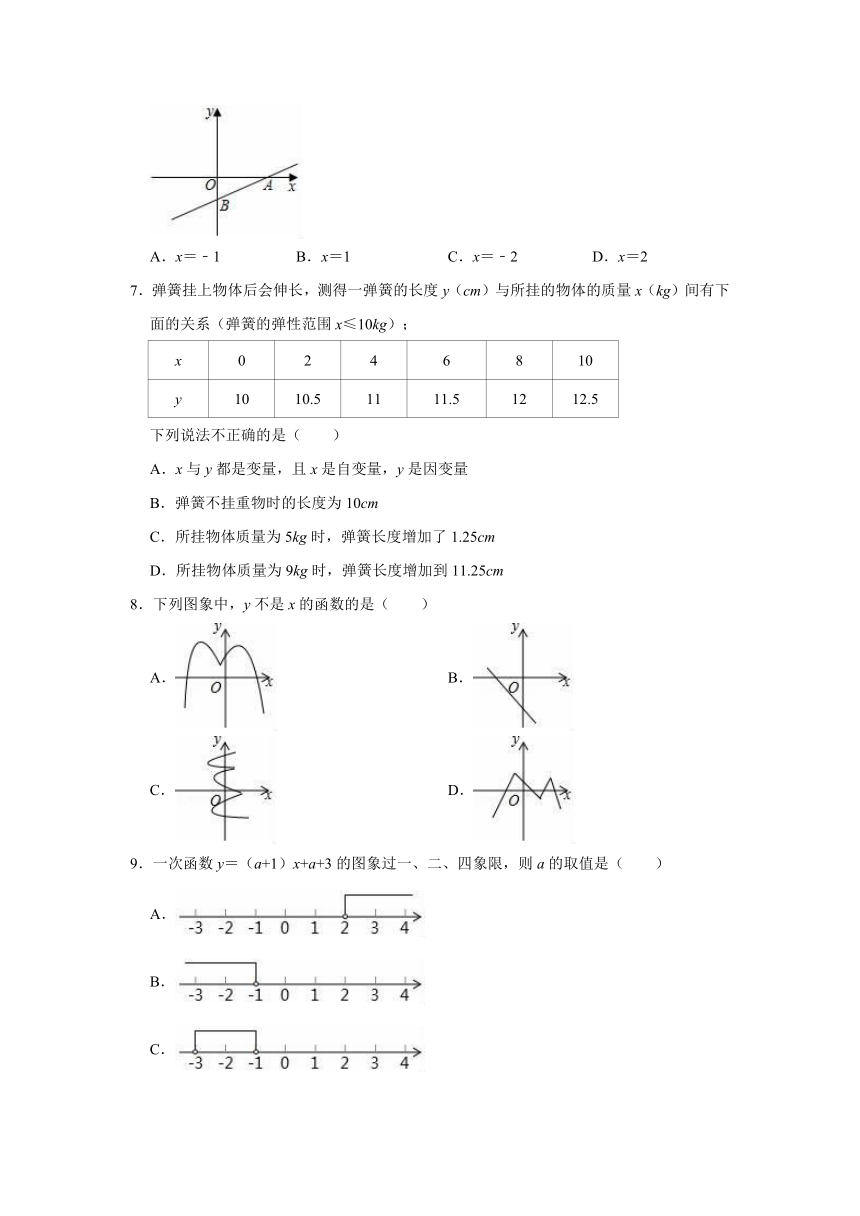
6.如图,y=kx+b(k≠0)过点A(2,0)和点B(0,﹣1),则方程kx+b=0解是( )
A.x=﹣1
B.x=1
C.x=﹣2
D.x=2
7.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg);
x
0
2
4
6
8
10
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
8.下列图象中,y不是x的函数的是( )
A.
B.
C.
D.
9.一次函数y=(a+1)x+a+3的图象过一、二、四象限,则a的取值是( )
A.
B.
C.
D.
10.在平面直角坐标系中,将直线y=kx﹣6沿x轴向左平移3个单位后恰好经过原点,则k的值为( )
A.﹣2
B.2
C.﹣3
D.3
二.填空题
11.若函数y=4x+3﹣a是正比例函数,则a=
.
12.已知正比例函数y=(1+)x,y随着x的增大而增大,则k的取值范围是
.
13.甲骑自行车、乙骑摩托车沿相同路线匀速由A地到B地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行
分钟时追上甲.
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,点B的横坐标a的取值范围是
.
15.如图,弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数,则弹簧不挂物体时的长度为
cm.
16.直线ax+y+a﹣3=0与直线(a+2)x+ay﹣2=0平行,则a的值为
.
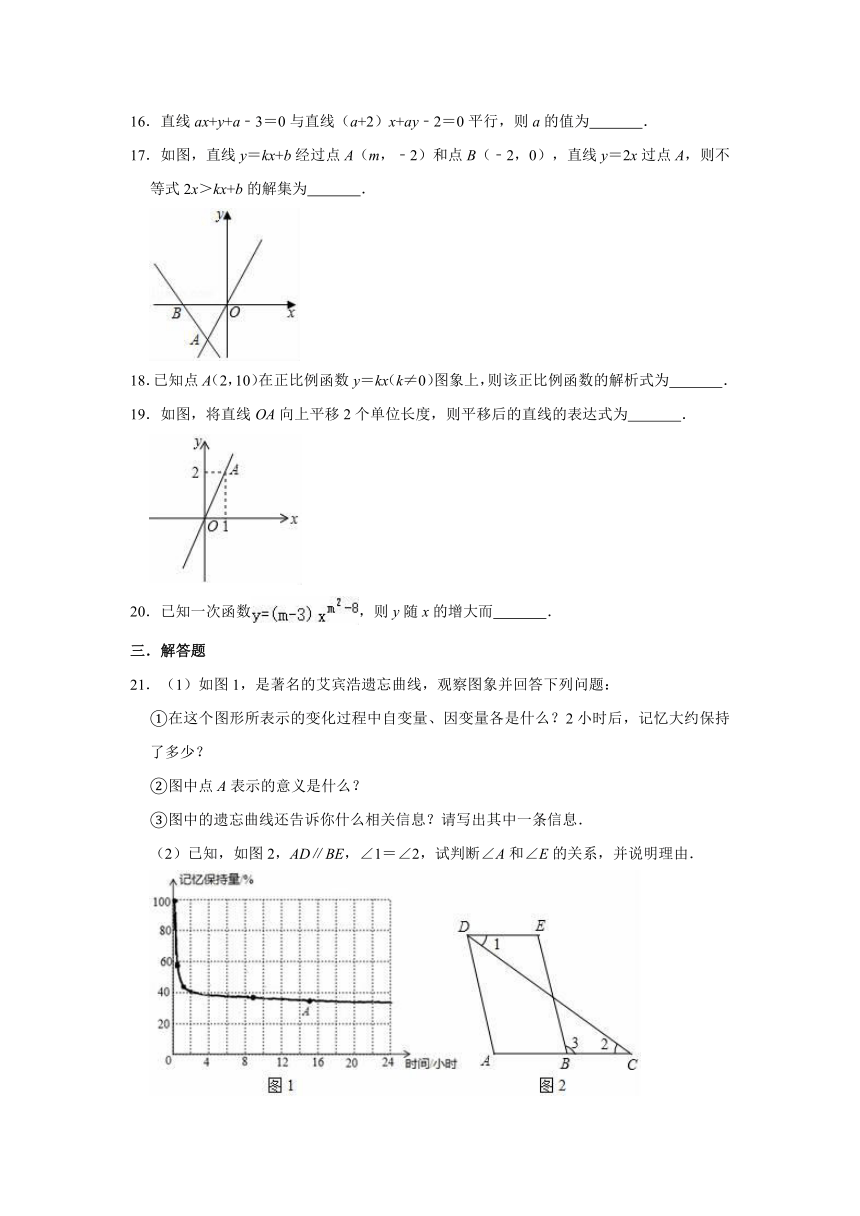
17.如图,直线y=kx+b经过点A(m,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x>kx+b的解集为
.
18.已知点A(2,10)在正比例函数y=kx(k≠0)图象上,则该正比例函数的解析式为
.
19.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
20.已知一次函数,则y随x的增大而
.
三.解答题
21.(1)如图1,是著名的艾宾浩遗忘曲线,观察图象并回答下列问题:
①在这个图形所表示的变化过程中自变量、因变量各是什么?2小时后,记忆大约保持了多少?
②图中点A表示的意义是什么?
③图中的遗忘曲线还告诉你什么相关信息?请写出其中一条信息.
(2)已知,如图2,AD∥BE,∠1=∠2,试判断∠A和∠E的关系,并说明理由.
22.一种豆子每千克售2元,豆子的总售价(y元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克)
0
0.5
1
1.5
2
2.5
3
5
总售价y(元)
0
1
2
3
4
5
6
10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
23.如图所示,在△ABC中,底边BC=8cm,高AD=6cm,E为AD上一动点,当点E从点D向点A运动时,△BEC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)若设DE长为x(cm),△BEC的面积为y,求y与x之间的关系式.
(3)当DE长度为3cm时,△BEC的面积y是多少?
24.已知函数y=(m﹣1)x+n,
(1)m为何值时,该函数是一次函数
(2)m、n为何值时,该函数是正比例函数
25.已知函数y=,m为常数.
(1)当m=1时,写出这个函数的表达式.并在所给坐标系中画出这个函数的图象.
(2)当点P(3,﹣3)在这个函数图象上时,求m的值;
(3)已知线段MN的两个端点坐标分别为M(﹣2,﹣1)、N(2,﹣1),当此函数的图象与线段MN只有一个交点时.直接写出m的取值范围.
26.如图,已知直线y=﹣x+3分别与x轴、y轴交于D、A两点;直线y=2x﹣1与y轴交于B点,与直线y=﹣x+3交于C点.
(1)求点B的坐标;
(2)求三角形ABC的面积.
27.已知函数y=a(x﹣1)2++1(a≠0),某兴趣小组对其图象与性质进行了探究,请补充完整探究过程.
x
…
﹣3
﹣2
﹣1
1
2
3
4
5
…
y
…
﹣6
﹣2
2
﹣2
﹣1
﹣2
m
﹣
…
(1)请根据给定条件直接写出a,b,m的值;
(2)如图已经画出了该函数的部分图象,请你根据上表中的数据在平面直角坐标系中描点、连线,补全该函数图象,并写出该函数的一条性质;
(3)若a(x﹣1)2+≥x﹣4,结合图象,直接写出x的取值范围.
参考答案与试题解析
一.选择题
1.解:小丽的微信红包原有100元钱,她在新年一周里抢红包,红包里的钱随着时间的变化而变化,在上述过程中,自变量是时间,
故选:A.
2.解:①y=﹣x;②y=;④y=2x+1是一次函数,共3个,
故选:C.
3.解:在运动过程中,汽车行驶的路程s随行驶的时间t的变化而变化,
∴s、t是变量,
汽车行驶的速度为50km/h,
∴50是常量,
故选:B.
4.解:∵函数y=,
∴x﹣5≥0,
∴x≥5,
故选:C.
5.解:由题意可知:
A、每月上网不足25小时,选择A方式最省钱,故本选项不合题意;
B、每月上网时间为30小时,选择A方式的费用为:30+5×[(120﹣30)÷(50﹣25)]=48(元),B方式为50元,C方式为120元,所以选择A方式最省钱,故本选项符合题意;
C、每月上网费用为60元,选择B方式比A方式时间长,故本选项不合题意;
D、每月上网时间超过70小时,选择C方式最省钱,故本选项不合题意;
故选:B.
6.解:∵y=kx+b(k≠0)过点A(2,0),
∴x=2时,y=0,
∴方程kx+b=0解是x=2.
故选:D.
7.解:A.x与y都是变量,且x是自变量,y是因变量,故A不符合题意;
B.弹簧不挂重物时的长度为10cm,故B不符合题意;
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm,故C不符合题意;
D.所挂物体质量为9kg时,弹簧长度增加到12.25cm,故D符号题意.
故选:D.
8.解:根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.而C中的y的值不具有唯一性,所以不是函数图象.
故选:C.
9.解:∵一次函数y=(a+1)x+a+3的图象过一、二、四象限,
∴a+1<0,a+3>0
解得﹣3<a<﹣1.
故选:C.
10.解:将直线y=kx﹣6沿x轴向左平移3个单位后得到y=k(x+3)﹣6,
∵经过原点,
∴0=k(0+3)﹣6,解得k=2,
故选:B.
二.填空题
11.解:由题意得:3﹣a=0,
解得:a=3,
故答案为:3.
12.解:∵正比例函数y=(1+)x中,y随x的增大而增大,
∴1+>0,
即k>﹣5.
故答案为:k>﹣5.
13.解:由题意得:
甲的速度为:(km/min),
乙的速度为:(km/min),
设乙在甲骑行x分钟时追上甲,根据题意得:
0.2x=0.4(x﹣10),
解得x=20.
所以乙在甲骑行20分钟时追上甲.
故答案为:20.
14.解:由图可得,点B的横坐标a的取值范围是
15.解:设弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=kx+b,
,
解得,,
即弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=0.5x+12,
当x=0时,y=12,
即弹簧不挂物体时的长度为12cm,
故答案为:12.
16.解:∵直线ax+y+a﹣3=0与直线(a+2)x+ay﹣2=0平行,
∴a=,a﹣3≠﹣2
解得a=2或﹣1,
故答案为2或﹣1.
17.解:观察图象可知,当x>﹣1时,直线y=2x落在直线y=kx+b的上方,
所以不等式2x>kx+b的解集为x>﹣1.
故答案为x>﹣1.
18.解:把A(2,10)代入y=kx得2k=10,解得k=5,
所以正比例函数解析式为y=5x.
故答案为:y=5x.
19.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
20.解:∵一次函数,
∴,
解得,m=﹣3,
∴一次函数y=﹣6x,
∴该函数y随x的增大而减小,
故答案为:减小.
三.解答题
21.解:(1)①根据图象可知:记忆的保存量随时间的变化而变化,
∴在这个图形所表示的变化过程中自变量是时间、因变量是记忆的保持量,
2小时后,记忆大约保持了40%;
②图中点A表示的意义是15小时后,记忆的保持量是多少;
③图中的遗忘曲线还告诉我随时间的加长,人的记忆保持量会逐渐减少,两个小时内减少的最快.
(2)∠A与=∠E,
理由:∵AD∥BE,
∴∠A=∠3,
又∵∠1=∠2,
∴DE∥AB,
∴∠E=∠3,
∴∠A=∠E.
22.解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是多少40元.
23.解:(1)在这个变化过程中,自变量为DE的长,因变量是△BEC的面积;
(2)y=×BC×DE=4x(0≤x≤6);
(3)当x=3时,y=4×3=12(cm2).
24.解:(1)∵函数y=(m﹣1)x+n,
∴当m﹣1≠0时,该函数是一次函数,即m≠1;
(2)当m≠1,且n=0时,该函数是正比例函数.
25.解:(1)m=1时.函数表达式为:y=,
图象如右图所示;
(2)①当m≥3时,则3+m=﹣3,
解得m=﹣6(舍去);
②当m<3时,则﹣2×3+2m=﹣3,
解得m=;
由上可得,m的值为;
(3)把M(﹣2,﹣1)代入y=,得m=1或m=;
把N(2,﹣1)代入y=,得m=﹣3或m=﹣;
∴函数的图象与线段MN只有一个交点时.﹣3≤m<﹣或1≤m<.
26.解:(1)在直线y=2x﹣1中,令x=0,则y=2x﹣1=﹣1,
故B的坐标是(0,﹣1);
(2)由直线y=﹣x+3可知A(0,3),
由,解得.
∴交点C(,2),
△ABC的面积=×(3+1)×=3.
27.解:(1)把(﹣1,2)和(1,﹣2)代入函数y=a(x﹣1)2++1中得:
,解得:,
∴y=﹣(x﹣1)2﹣+1(a≠0),
当x=4时,m=﹣﹣+1=﹣;
(2)如图所示,
性质:当x>2时,y随x的增大而减小(答案不唯一);
(3)∵a(x﹣1)2+≥x﹣4,
∴a(x﹣1)2++1≥x﹣3,
如图所示,
由图象得:x的取值范围是﹣3≤x<0或1≤x≤2.
一次函数》单元测试卷
一.选择题
1.小丽的微信红包原有100元钱,她在新年一周里抢红包,红包里的钱随着时间的变化而变化,在上述过程中,自变量是( )
A.时间
B.小丽
C.80元
D.红包里的钱
2.下列函数中:①y=﹣x;②y=;③y=;④y=2x+1,其中一次函数的个数是( )
A.1
B.2
C.3
D.4
3.已知一辆汽车行驶的速度为50km/h,它行驶的路程s(单位:千米)与行驶的时间t(单位:小时)之间的关系是s=50t,其中常量是( )
A.s
B.50
C.t
D.s和t
4.函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
5.某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是( )
A.每月上网不足25小时,选择A方式最省钱
B.每月上网时间为30小时,选择B方式最省钱
C.每月上网费用为60元,选择B方式比A方式时间长
D.每月上网时间超过70小时,选择C方式最省钱
6.如图,y=kx+b(k≠0)过点A(2,0)和点B(0,﹣1),则方程kx+b=0解是( )
A.x=﹣1
B.x=1
C.x=﹣2
D.x=2
7.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系(弹簧的弹性范围x≤10kg);
x
0
2
4
6
8
10
y
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为10cm
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm
D.所挂物体质量为9kg时,弹簧长度增加到11.25cm
8.下列图象中,y不是x的函数的是( )
A.
B.
C.
D.
9.一次函数y=(a+1)x+a+3的图象过一、二、四象限,则a的取值是( )
A.
B.
C.
D.
10.在平面直角坐标系中,将直线y=kx﹣6沿x轴向左平移3个单位后恰好经过原点,则k的值为( )
A.﹣2
B.2
C.﹣3
D.3
二.填空题
11.若函数y=4x+3﹣a是正比例函数,则a=
.
12.已知正比例函数y=(1+)x,y随着x的增大而增大,则k的取值范围是
.
13.甲骑自行车、乙骑摩托车沿相同路线匀速由A地到B地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行
分钟时追上甲.
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,点B的横坐标a的取值范围是
.
15.如图,弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数,则弹簧不挂物体时的长度为
cm.
16.直线ax+y+a﹣3=0与直线(a+2)x+ay﹣2=0平行,则a的值为
.
17.如图,直线y=kx+b经过点A(m,﹣2)和点B(﹣2,0),直线y=2x过点A,则不等式2x>kx+b的解集为
.
18.已知点A(2,10)在正比例函数y=kx(k≠0)图象上,则该正比例函数的解析式为
.
19.如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为
.
20.已知一次函数,则y随x的增大而
.
三.解答题
21.(1)如图1,是著名的艾宾浩遗忘曲线,观察图象并回答下列问题:
①在这个图形所表示的变化过程中自变量、因变量各是什么?2小时后,记忆大约保持了多少?
②图中点A表示的意义是什么?
③图中的遗忘曲线还告诉你什么相关信息?请写出其中一条信息.
(2)已知,如图2,AD∥BE,∠1=∠2,试判断∠A和∠E的关系,并说明理由.
22.一种豆子每千克售2元,豆子的总售价(y元)与所售豆子的质量x(千克)之间的关系如下表:
售出豆子质量x(千克)
0
0.5
1
1.5
2
2.5
3
5
总售价y(元)
0
1
2
3
4
5
6
10
(1)在这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当豆子售出5千克时,总售价是多少?
(3)按表中给出的关系,用一个式子把x与y之间的关系表示出来.
(4)当豆子售出20千克时,总售价是多少?
23.如图所示,在△ABC中,底边BC=8cm,高AD=6cm,E为AD上一动点,当点E从点D向点A运动时,△BEC的面积发生了变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)若设DE长为x(cm),△BEC的面积为y,求y与x之间的关系式.
(3)当DE长度为3cm时,△BEC的面积y是多少?
24.已知函数y=(m﹣1)x+n,
(1)m为何值时,该函数是一次函数
(2)m、n为何值时,该函数是正比例函数
25.已知函数y=,m为常数.
(1)当m=1时,写出这个函数的表达式.并在所给坐标系中画出这个函数的图象.
(2)当点P(3,﹣3)在这个函数图象上时,求m的值;
(3)已知线段MN的两个端点坐标分别为M(﹣2,﹣1)、N(2,﹣1),当此函数的图象与线段MN只有一个交点时.直接写出m的取值范围.
26.如图,已知直线y=﹣x+3分别与x轴、y轴交于D、A两点;直线y=2x﹣1与y轴交于B点,与直线y=﹣x+3交于C点.
(1)求点B的坐标;
(2)求三角形ABC的面积.
27.已知函数y=a(x﹣1)2++1(a≠0),某兴趣小组对其图象与性质进行了探究,请补充完整探究过程.
x
…
﹣3
﹣2
﹣1
1
2
3
4
5
…
y
…
﹣6
﹣2
2
﹣2
﹣1
﹣2
m
﹣
…
(1)请根据给定条件直接写出a,b,m的值;
(2)如图已经画出了该函数的部分图象,请你根据上表中的数据在平面直角坐标系中描点、连线,补全该函数图象,并写出该函数的一条性质;
(3)若a(x﹣1)2+≥x﹣4,结合图象,直接写出x的取值范围.
参考答案与试题解析
一.选择题
1.解:小丽的微信红包原有100元钱,她在新年一周里抢红包,红包里的钱随着时间的变化而变化,在上述过程中,自变量是时间,
故选:A.
2.解:①y=﹣x;②y=;④y=2x+1是一次函数,共3个,
故选:C.
3.解:在运动过程中,汽车行驶的路程s随行驶的时间t的变化而变化,
∴s、t是变量,
汽车行驶的速度为50km/h,
∴50是常量,
故选:B.
4.解:∵函数y=,
∴x﹣5≥0,
∴x≥5,
故选:C.
5.解:由题意可知:
A、每月上网不足25小时,选择A方式最省钱,故本选项不合题意;
B、每月上网时间为30小时,选择A方式的费用为:30+5×[(120﹣30)÷(50﹣25)]=48(元),B方式为50元,C方式为120元,所以选择A方式最省钱,故本选项符合题意;
C、每月上网费用为60元,选择B方式比A方式时间长,故本选项不合题意;
D、每月上网时间超过70小时,选择C方式最省钱,故本选项不合题意;
故选:B.
6.解:∵y=kx+b(k≠0)过点A(2,0),
∴x=2时,y=0,
∴方程kx+b=0解是x=2.
故选:D.
7.解:A.x与y都是变量,且x是自变量,y是因变量,故A不符合题意;
B.弹簧不挂重物时的长度为10cm,故B不符合题意;
C.所挂物体质量为5kg时,弹簧长度增加了1.25cm,故C不符合题意;
D.所挂物体质量为9kg时,弹簧长度增加到12.25cm,故D符号题意.
故选:D.
8.解:根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.而C中的y的值不具有唯一性,所以不是函数图象.
故选:C.
9.解:∵一次函数y=(a+1)x+a+3的图象过一、二、四象限,
∴a+1<0,a+3>0
解得﹣3<a<﹣1.
故选:C.
10.解:将直线y=kx﹣6沿x轴向左平移3个单位后得到y=k(x+3)﹣6,
∵经过原点,
∴0=k(0+3)﹣6,解得k=2,
故选:B.
二.填空题
11.解:由题意得:3﹣a=0,
解得:a=3,
故答案为:3.
12.解:∵正比例函数y=(1+)x中,y随x的增大而增大,
∴1+>0,
即k>﹣5.
故答案为:k>﹣5.
13.解:由题意得:
甲的速度为:(km/min),
乙的速度为:(km/min),
设乙在甲骑行x分钟时追上甲,根据题意得:
0.2x=0.4(x﹣10),
解得x=20.
所以乙在甲骑行20分钟时追上甲.
故答案为:20.
14.解:由图可得,点B的横坐标a的取值范围是
15.解:设弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=kx+b,
,
解得,,
即弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=0.5x+12,
当x=0时,y=12,
即弹簧不挂物体时的长度为12cm,
故答案为:12.
16.解:∵直线ax+y+a﹣3=0与直线(a+2)x+ay﹣2=0平行,
∴a=,a﹣3≠﹣2
解得a=2或﹣1,
故答案为2或﹣1.
17.解:观察图象可知,当x>﹣1时,直线y=2x落在直线y=kx+b的上方,
所以不等式2x>kx+b的解集为x>﹣1.
故答案为x>﹣1.
18.解:把A(2,10)代入y=kx得2k=10,解得k=5,
所以正比例函数解析式为y=5x.
故答案为:y=5x.
19.解:设直线OA的解析式为:y=kx,
把(1,2)代入,得k=2,
则直线OA解析式是:y=2x.
将其上平移2个单位长度,则平移后的直线的表达式为:y=2x+2.
故答案是:y=2x+2.
20.解:∵一次函数,
∴,
解得,m=﹣3,
∴一次函数y=﹣6x,
∴该函数y随x的增大而减小,
故答案为:减小.
三.解答题
21.解:(1)①根据图象可知:记忆的保存量随时间的变化而变化,
∴在这个图形所表示的变化过程中自变量是时间、因变量是记忆的保持量,
2小时后,记忆大约保持了40%;
②图中点A表示的意义是15小时后,记忆的保持量是多少;
③图中的遗忘曲线还告诉我随时间的加长,人的记忆保持量会逐渐减少,两个小时内减少的最快.
(2)∠A与=∠E,
理由:∵AD∥BE,
∴∠A=∠3,
又∵∠1=∠2,
∴DE∥AB,
∴∠E=∠3,
∴∠A=∠E.
22.解:(1)表格中反映的是售出豆子质量x(千克)与总售价y(元)之间的关系,售出豆子的质量x(千克)是自变量,总售价y(元)是因变量;
(2)由图表可知,
售出5千克时,总售价为10元;
(3)设x与y之间的关系为:y=kx,
把x=1,y=2代入上式,
得k=2,
x与y之间的关系为y=2x;
(4)当豆子售出20千克时,
y=2×20=40(元),
当豆子售出20千克时,总售价是多少40元.
23.解:(1)在这个变化过程中,自变量为DE的长,因变量是△BEC的面积;
(2)y=×BC×DE=4x(0≤x≤6);
(3)当x=3时,y=4×3=12(cm2).
24.解:(1)∵函数y=(m﹣1)x+n,
∴当m﹣1≠0时,该函数是一次函数,即m≠1;
(2)当m≠1,且n=0时,该函数是正比例函数.
25.解:(1)m=1时.函数表达式为:y=,
图象如右图所示;
(2)①当m≥3时,则3+m=﹣3,
解得m=﹣6(舍去);
②当m<3时,则﹣2×3+2m=﹣3,
解得m=;
由上可得,m的值为;
(3)把M(﹣2,﹣1)代入y=,得m=1或m=;
把N(2,﹣1)代入y=,得m=﹣3或m=﹣;
∴函数的图象与线段MN只有一个交点时.﹣3≤m<﹣或1≤m<.
26.解:(1)在直线y=2x﹣1中,令x=0,则y=2x﹣1=﹣1,
故B的坐标是(0,﹣1);
(2)由直线y=﹣x+3可知A(0,3),
由,解得.
∴交点C(,2),
△ABC的面积=×(3+1)×=3.
27.解:(1)把(﹣1,2)和(1,﹣2)代入函数y=a(x﹣1)2++1中得:
,解得:,
∴y=﹣(x﹣1)2﹣+1(a≠0),
当x=4时,m=﹣﹣+1=﹣;
(2)如图所示,
性质:当x>2时,y随x的增大而减小(答案不唯一);
(3)∵a(x﹣1)2+≥x﹣4,
∴a(x﹣1)2++1≥x﹣3,
如图所示,
由图象得:x的取值范围是﹣3≤x<0或1≤x≤2.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
