浙教版初中数学八上 1.5.1 SSS及SAS的判定 课件(25张)
文档属性
| 名称 | 浙教版初中数学八上 1.5.1 SSS及SAS的判定 课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 816.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 17:25:13 | ||
图片预览


文档简介
(共25张PPT)
判定两个三角形全等“边角边”定理
1、当木板门松动时,加钉一块斜木条就好了,这是应用了一个什么数学知识?
2、三角形全等的判定方法
——“边边边”(SSS)定理的内容是什么?
回顾与思考
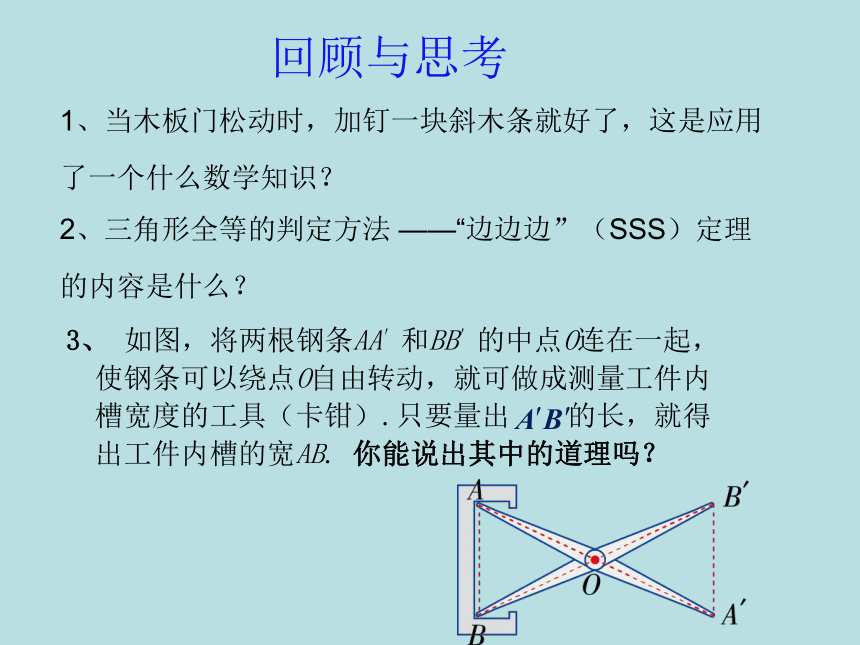
3、
如图,将两根钢条AA′和BB′的中点O连在一起,
使钢条可以绕点O自由转动,就可做成测量工件内
槽宽度的工具(卡钳).只要量出
的长,就得
出工件内槽的宽AB.
你能说出其中的道理吗?
叠一叠
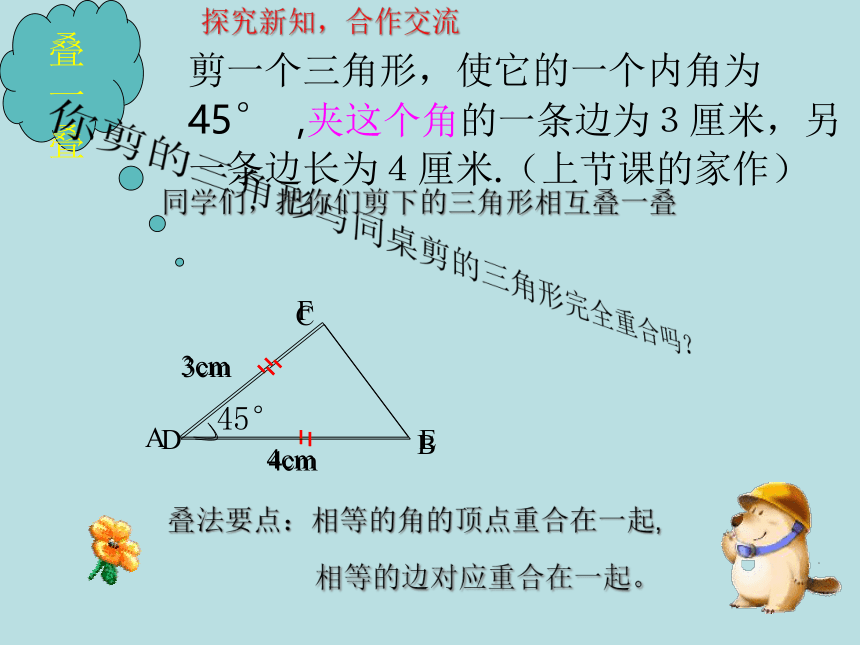
剪一个三角形,使它的一个内角为45°
,夹这个角的一条边为3厘米,另一条边长为4厘米.(上节课的家作)
4cm
3cm
45°
A
B
C
4cm
3cm
D
E
F
你剪的三角形与同桌剪的三角形完全重合吗?
叠法要点:相等的角的顶点重合在一起,
相等的边对应重合在一起。
同学们,把你们剪下的三角形相互叠一叠
探究新知,合作交流
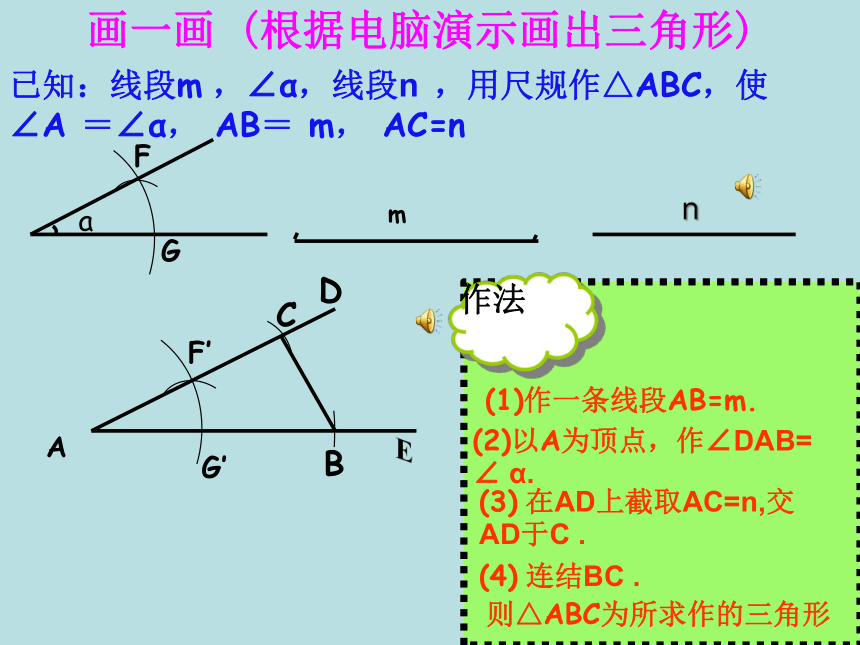
已知:线段m
,∠α,线段n
,用尺规作△ABC,使∠A
=∠α,
AB=
m,
AC=n
m
a
B
G
F
G′
F′
D
A
(1)作一条线段AB=m.
(2)以A为顶点,作∠DAB=
∠
α.
(3)
在AD上截取AC=n,交AD于C
.
则△ABC为所求作的三角形
作法
C
(4)
连结BC
.
画一画
(根据电脑演示画出三角形)
E
n
各位同学把所画的三角形剪下来,当它们在不同位置时,聪明的你能不能用我们所学过的平移、旋转、轴反射等变换,把它们叠在一起,你有什么发现?
实践与探索
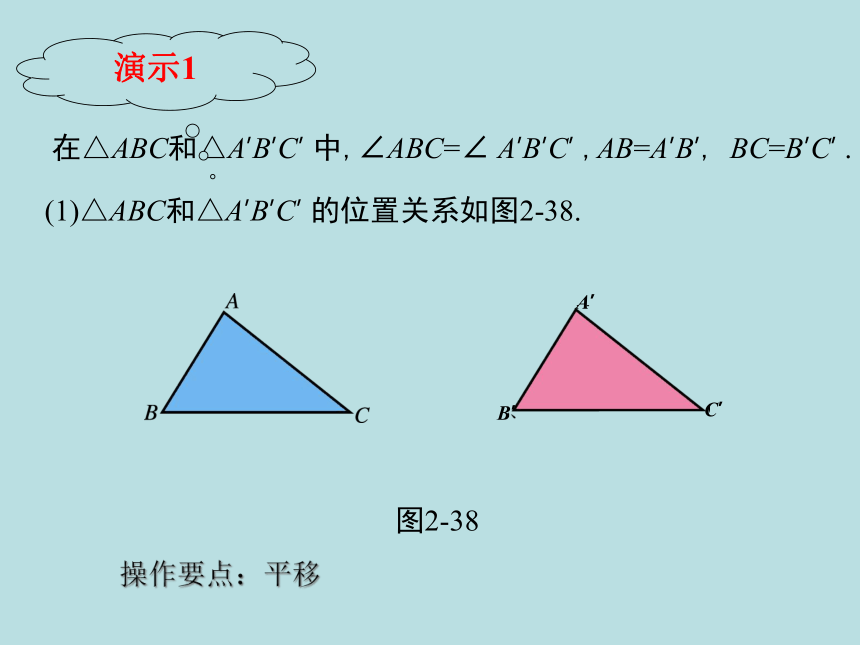
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
(1)△ABC和△A’B’C’
的位置关系如图2-38.
图2-38
A’
B’
C’
演示1
操作要点:平移
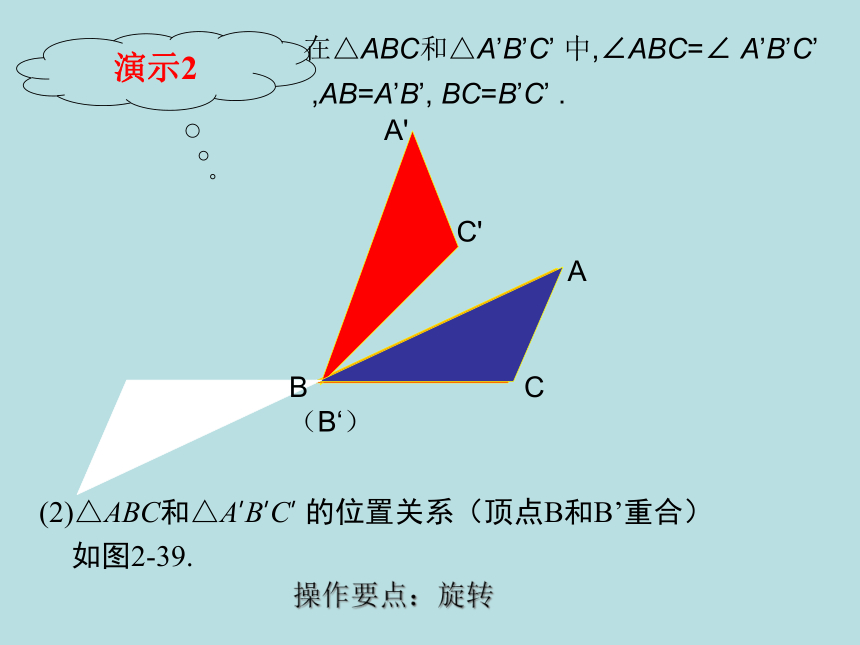
演示2
A'
C'
C
A
B(B‘)
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
(2)△ABC和△A’B’C’
的位置关系(顶点B和B’重合)如图2-39.
操作要点:旋转
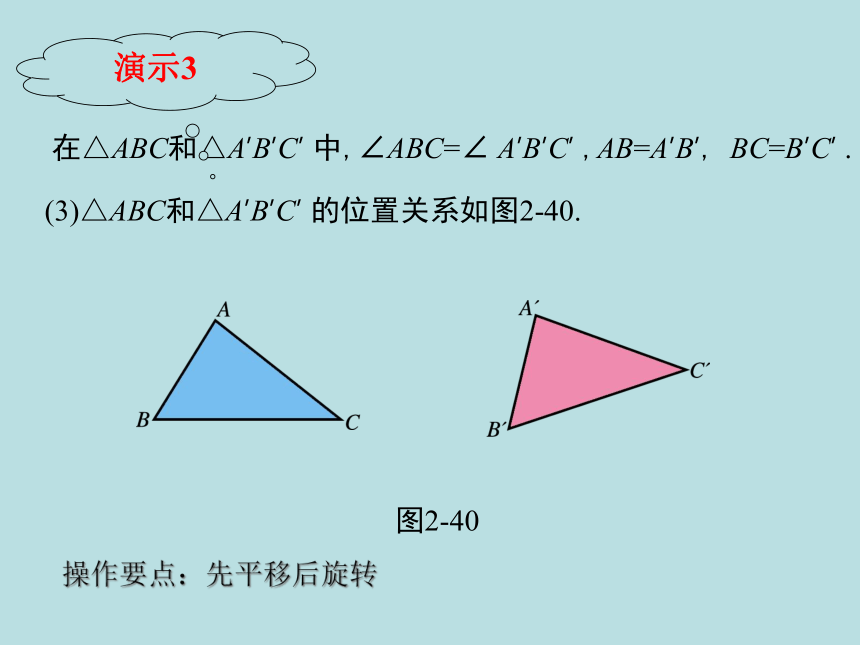
(3)△ABC和△A’B’C’
的位置关系如图2-40.
图2-40
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
演示3
操作要点:先平移后旋转
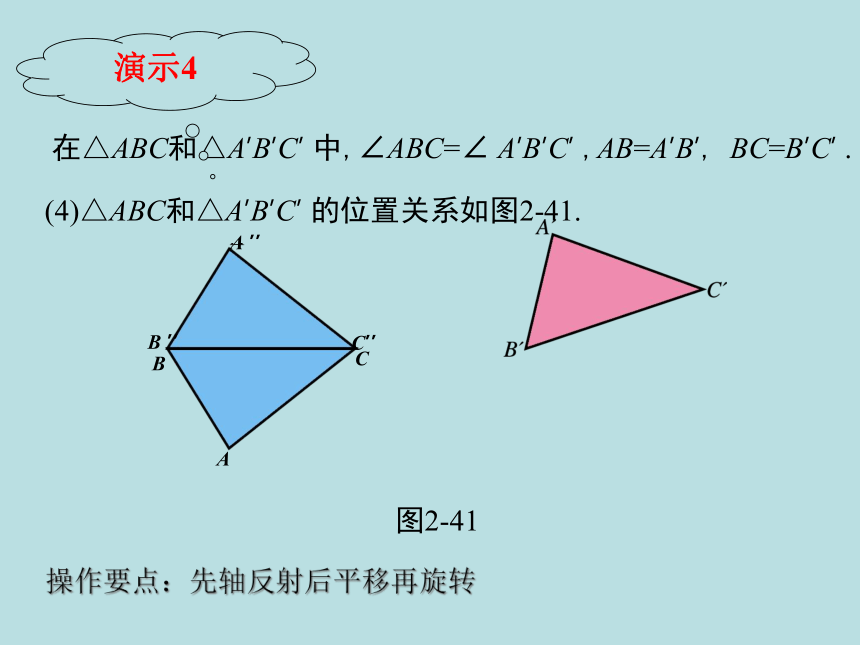
(4)△ABC和△A’B’C’
的位置关系如图2-41.
图2-41
C
A
B
A
’’
B
’’
C’’
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
演示4
操作要点:先轴反射后平移再旋转
由此,聪明的你可以得出什么结论?
实践与探索
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为“边角边”或“SAS”)
结论:
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
是夹角哦!
∵
用数学语言表述全等三角形判定(二)
——SAS
一般来说,等式左边是前一个三角形的边角,等号右边是另一个三角形的边角
1.在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
Ⅳ
8
cm
5
cm
Ⅱ
30?
?
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
Ⅲ
巩固练习
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
2、若AB=AC
则添加什么条件(较少)可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD=∠CAD
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
A
B
D
O
C
解 在△
ACO和△
BDO中,
AO=BO
CO=DO
∠AOC=
∠
BOD
(对顶角相等)
△
AOC≌△
BOD
(SAS
)
∵
∴
例
如图,已知AB和CD相交与O,
且
OA=OB,
OC=OD.
求证:△
OAD≌△
OBC
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
应用
格式要求:先指出在哪两个三角形中证全等;再按SAS顺序列出三个条件,并用括号把它们括在一起;写出结论.
找已知条件:已知中找,图形中看.
1.
如图,将两根钢条AA′和BB′的中点O连在一起,
使钢条可以绕点O自由转动,就可做成测量工件内
槽宽度的工具(卡钳).只要量出
的长,就得
出工件内槽的宽AB.
这是根据什么道理呢?
解
△ABO≌△A′B′O(SAS)
∴AB=
A′B′.
说一说
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
2.
如图,AD∥BC,AD=BC.
问:△ADC和△CBA
是全等三角形吗?为什么?
解:∵AD∥BC
∴∠DAC=∠BCA
在△ADC和△CBA中
∵
AD=BC
∠DAC=∠BCA
AC=CA
∴△ADC≌△CBA (SAS)
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
想一想
3、已知:如图,AB=AC,点E,F分别是AC,AB的中点,求证:BE=CF
解:∵AB=ACE,E、F分别是
AC,AB的中点
在⊿ABE和⊿ACF中,
AB=AC
∴⊿ABE≌⊿CBE(SAS)
∵
∴BE=CF
∴AE=AF
∠A=∠A
AE=AF
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
证一证
如果已知两个三角形有两边和一角对应相等时,应分为几种情形?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
边边角成立吗?
反馈提高
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为45°
,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
45°
45°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
画一画
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
A
B
A’
M
B’
AB
=
A’B’
∠B
=
∠B’
BC
=B’C’
△
ABC≌
△A’B’C’(SAS)
A
B
C
A’
B’
C’
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
如图,AB=AE,∠B=∠E,BC=DE,点F是CD的中点.试说明:AF⊥CD.
证明:连结AC,AD
在△ABC和△AED中:
拓展训练
∵
AB=AE(已知)
∠B=∠E(已知)
BC=DE(已知)
∴
△ABC≌
△AED(S.A.S)
∴
AC=AD(全等三角形对应边相等)
又∵点F是CD的中点
∴AF⊥CD(等腰三角形三线合一)
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
1、今天我们学习哪种方法判定两三角形全等?
答:边角边(S.A.S)
2
、已知三角形两边及其夹角可以画出这个三角形。
到了什么?
今天你学
说一说
3、思考
:“边边角”能不能判定两个三角形全等”?
(不能)
4、数学来源于生活,又应用于生活,
生活中处处有数学知识,我们要做一
个有心人,就一定能够学好数学!
作业提示
1、P87习题A---2
2、用所学的“边角边”内容,编一道与生活有联系的题
驶向胜利的彼岸
谢谢!
再见
判定两个三角形全等“边角边”定理
1、当木板门松动时,加钉一块斜木条就好了,这是应用了一个什么数学知识?
2、三角形全等的判定方法
——“边边边”(SSS)定理的内容是什么?
回顾与思考
3、
如图,将两根钢条AA′和BB′的中点O连在一起,
使钢条可以绕点O自由转动,就可做成测量工件内
槽宽度的工具(卡钳).只要量出
的长,就得
出工件内槽的宽AB.
你能说出其中的道理吗?
叠一叠
剪一个三角形,使它的一个内角为45°
,夹这个角的一条边为3厘米,另一条边长为4厘米.(上节课的家作)
4cm
3cm
45°
A
B
C
4cm
3cm
D
E
F
你剪的三角形与同桌剪的三角形完全重合吗?
叠法要点:相等的角的顶点重合在一起,
相等的边对应重合在一起。
同学们,把你们剪下的三角形相互叠一叠
探究新知,合作交流
已知:线段m
,∠α,线段n
,用尺规作△ABC,使∠A
=∠α,
AB=
m,
AC=n
m
a
B
G
F
G′
F′
D
A
(1)作一条线段AB=m.
(2)以A为顶点,作∠DAB=
∠
α.
(3)
在AD上截取AC=n,交AD于C
.
则△ABC为所求作的三角形
作法
C
(4)
连结BC
.
画一画
(根据电脑演示画出三角形)
E
n
各位同学把所画的三角形剪下来,当它们在不同位置时,聪明的你能不能用我们所学过的平移、旋转、轴反射等变换,把它们叠在一起,你有什么发现?
实践与探索
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
(1)△ABC和△A’B’C’
的位置关系如图2-38.
图2-38
A’
B’
C’
演示1
操作要点:平移
演示2
A'
C'
C
A
B(B‘)
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
(2)△ABC和△A’B’C’
的位置关系(顶点B和B’重合)如图2-39.
操作要点:旋转
(3)△ABC和△A’B’C’
的位置关系如图2-40.
图2-40
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
演示3
操作要点:先平移后旋转
(4)△ABC和△A’B’C’
的位置关系如图2-41.
图2-41
C
A
B
A
’’
B
’’
C’’
在△ABC和△A’B’C’
中,∠ABC=∠
A’B’C’
,AB=A’B’,
BC=B’C’
.
演示4
操作要点:先轴反射后平移再旋转
由此,聪明的你可以得出什么结论?
实践与探索
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为“边角边”或“SAS”)
结论:
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
是夹角哦!
∵
用数学语言表述全等三角形判定(二)
——SAS
一般来说,等式左边是前一个三角形的边角,等号右边是另一个三角形的边角
1.在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
?
30?
8
cm
9
cm
Ⅵ
?
30?
8
cm
8
cm
Ⅳ
Ⅳ
8
cm
5
cm
Ⅱ
30?
?
8
cm
5
cm
Ⅴ
30?
8
cm
?
5
cm
Ⅷ
8
cm
5
cm
?
30?
8
cm
9
cm
Ⅶ
Ⅲ
?
30?
8
cm
8
cm
Ⅲ
巩固练习
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
2、若AB=AC
则添加什么条件(较少)可得ΔABD≌ΔACD
A
D
B
C
ΔABD≌ΔACD
S
A
S
AD=AD
AB=AC
∠BAD=∠CAD
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
A
B
D
O
C
解 在△
ACO和△
BDO中,
AO=BO
CO=DO
∠AOC=
∠
BOD
(对顶角相等)
△
AOC≌△
BOD
(SAS
)
∵
∴
例
如图,已知AB和CD相交与O,
且
OA=OB,
OC=OD.
求证:△
OAD≌△
OBC
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
应用
格式要求:先指出在哪两个三角形中证全等;再按SAS顺序列出三个条件,并用括号把它们括在一起;写出结论.
找已知条件:已知中找,图形中看.
1.
如图,将两根钢条AA′和BB′的中点O连在一起,
使钢条可以绕点O自由转动,就可做成测量工件内
槽宽度的工具(卡钳).只要量出
的长,就得
出工件内槽的宽AB.
这是根据什么道理呢?
解
△ABO≌△A′B′O(SAS)
∴AB=
A′B′.
说一说
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
2.
如图,AD∥BC,AD=BC.
问:△ADC和△CBA
是全等三角形吗?为什么?
解:∵AD∥BC
∴∠DAC=∠BCA
在△ADC和△CBA中
∵
AD=BC
∠DAC=∠BCA
AC=CA
∴△ADC≌△CBA (SAS)
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
想一想
3、已知:如图,AB=AC,点E,F分别是AC,AB的中点,求证:BE=CF
解:∵AB=ACE,E、F分别是
AC,AB的中点
在⊿ABE和⊿ACF中,
AB=AC
∴⊿ABE≌⊿CBE(SAS)
∵
∴BE=CF
∴AE=AF
∠A=∠A
AE=AF
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
证一证
如果已知两个三角形有两边和一角对应相等时,应分为几种情形?
边-角-边
边-边-角
A
A
A’
A’
B
B’
B
B’
C
C
C’
C’
边边角成立吗?
反馈提高
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为45°
,情况又怎样?动手画一画,你发现了什么?
A
B
C
D
E
F
2.5cm
3.5cm
45°
45°
3.5cm
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
画一画
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
A
B
A’
M
B’
AB
=
A’B’
∠B
=
∠B’
BC
=B’C’
△
ABC≌
△A’B’C’(SAS)
A
B
C
A’
B’
C’
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
如图,AB=AE,∠B=∠E,BC=DE,点F是CD的中点.试说明:AF⊥CD.
证明:连结AC,AD
在△ABC和△AED中:
拓展训练
∵
AB=AE(已知)
∠B=∠E(已知)
BC=DE(已知)
∴
△ABC≌
△AED(S.A.S)
∴
AC=AD(全等三角形对应边相等)
又∵点F是CD的中点
∴AF⊥CD(等腰三角形三线合一)
有两条边及它们的夹角对应相等的两个三角形全等(SAS)
1、今天我们学习哪种方法判定两三角形全等?
答:边角边(S.A.S)
2
、已知三角形两边及其夹角可以画出这个三角形。
到了什么?
今天你学
说一说
3、思考
:“边边角”能不能判定两个三角形全等”?
(不能)
4、数学来源于生活,又应用于生活,
生活中处处有数学知识,我们要做一
个有心人,就一定能够学好数学!
作业提示
1、P87习题A---2
2、用所学的“边角边”内容,编一道与生活有联系的题
驶向胜利的彼岸
谢谢!
再见
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
