浙教版初中数学八年级上册 1.4 全等三角形 课件(18张)
文档属性
| 名称 | 浙教版初中数学八年级上册 1.4 全等三角形 课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 358.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 18:50:58 | ||
图片预览

文档简介
(共18张PPT)
1.4
全等三角形
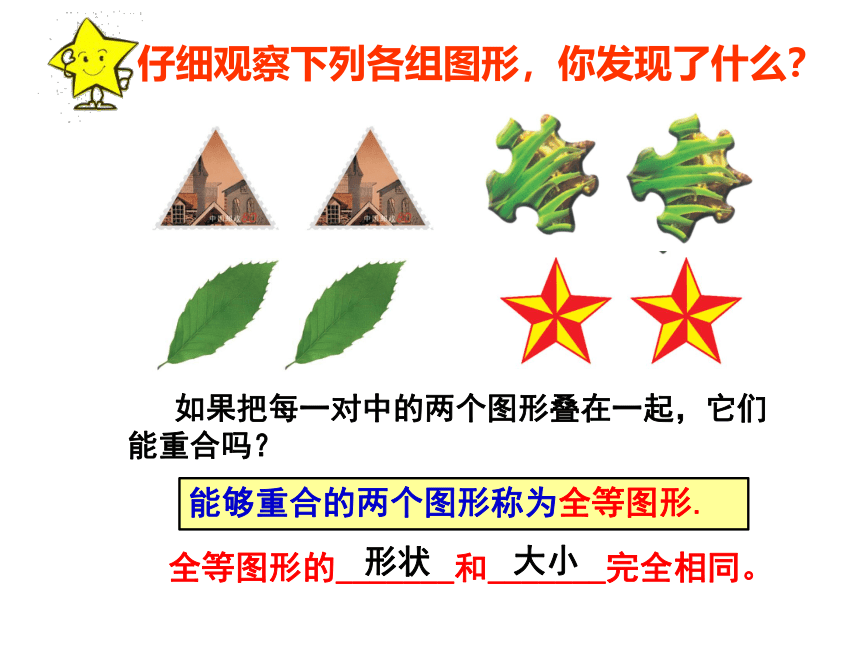
仔细观察下列各组图形,你发现了什么?
能够重合的两个图形称为全等图形.
如果把每一对中的两个图形叠在一起,它们能重合吗?
全等图形的_______和_______完全相同。
形状
大小
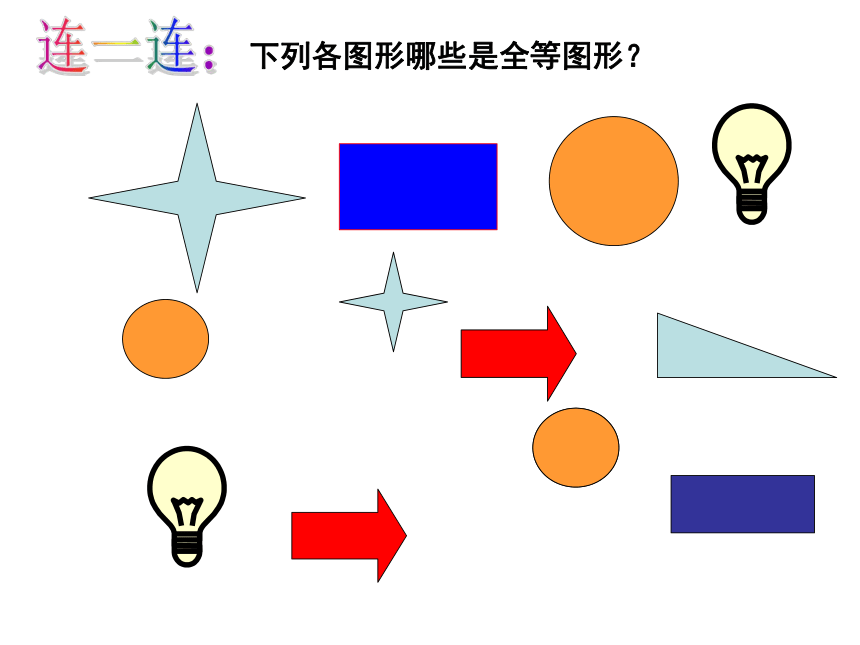
下列各图形哪些是全等图形?
连一连:
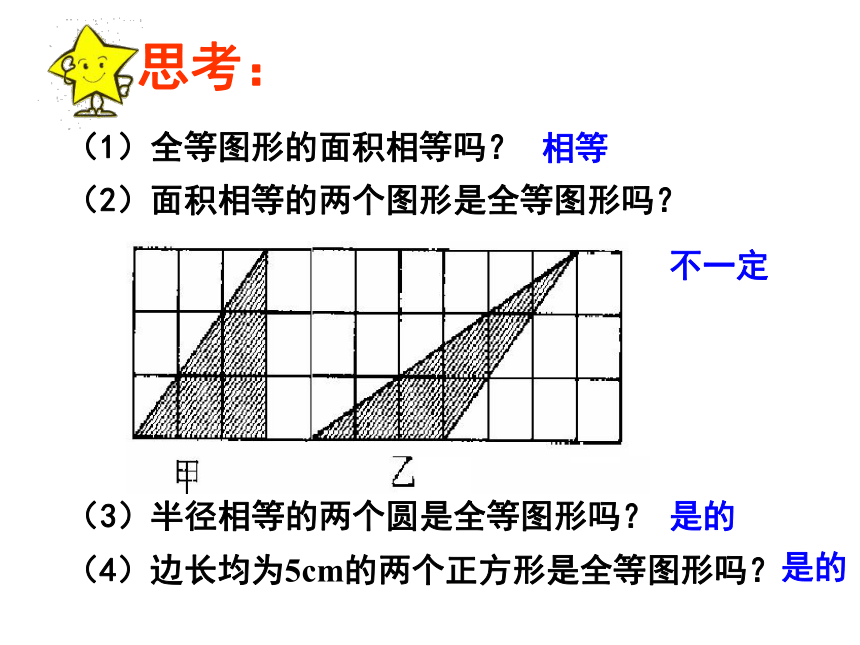
思考:
(2)面积相等的两个图形是全等图形吗?
(1)全等图形的面积相等吗?
相等
不一定
(3)半径相等的两个圆是全等图形吗?
是的
(4)边长均为5cm的两个正方形是全等图形吗?
是的
F
E
D
C
B
A
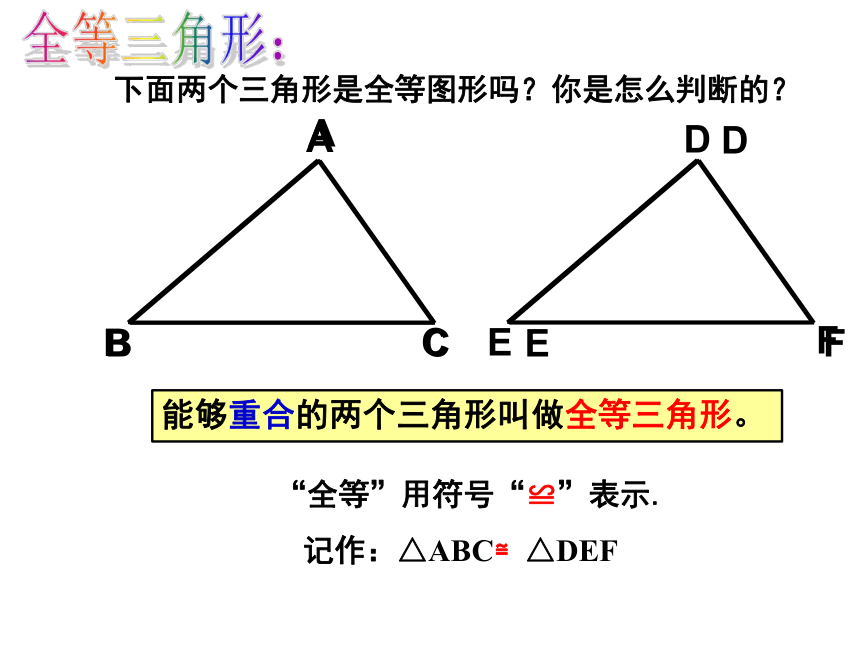
能够重合的两个三角形叫做全等三角形。
全等三角形:
下面两个三角形是全等图形吗?你是怎么判断的?
“全等”用符号“≌”表示.
记作:△ABC≌△DEF
F
E
D
C
B
A
F
E
D
C
B
A
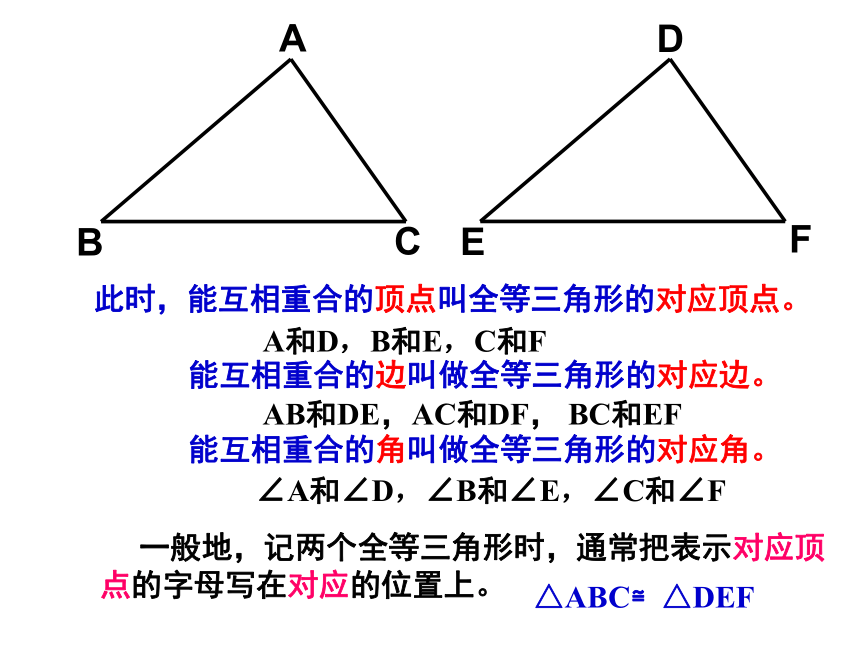
此时,能互相重合的顶点叫全等三角形的对应顶点。
能互相重合的边叫做全等三角形的对应边。
能互相重合的角叫做全等三角形的对应角。
A和D,B和E,C和F
AB和DE,AC和DF,
BC和EF
∠A和∠D,∠B和∠E,∠C和∠F
一般地,记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
△ABC≌△DEF
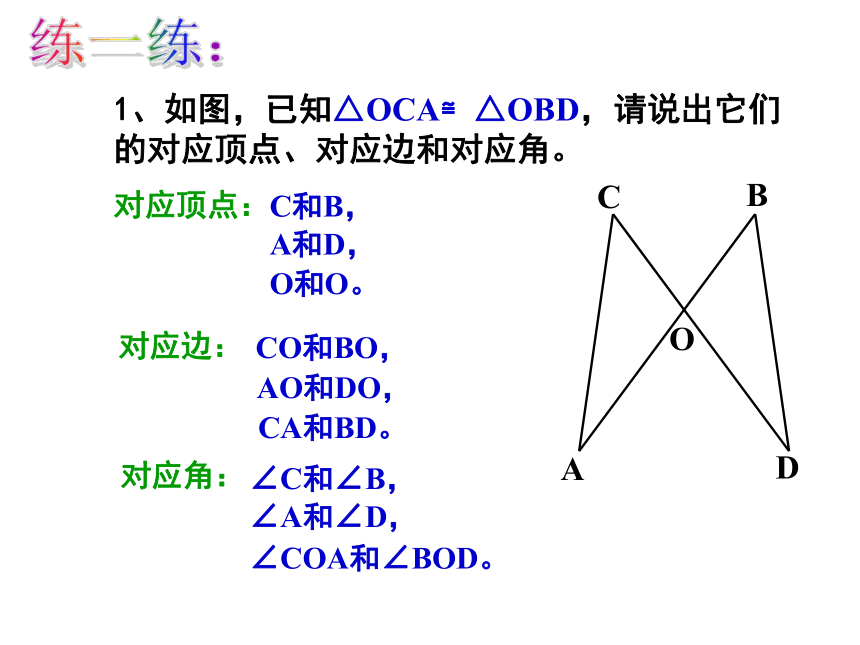
练一练:
1、如图,已知△OCA≌△OBD,请说出它们的对应顶点、对应边和对应角。
O
D
C
B
A
对应边:
对应顶点:
O和O。
C和B,
A和D,
CO和BO,
AO和DO,
CA和BD。
对应角:
∠A和∠D,
∠C和∠B,
∠COA和∠BOD。
练一练:
2、如图,已知△OCA与△ODB全等,用符号“≌”表示这两个三角形全等,已知∠A与∠B是对应角,写出其余的对应角和对应边。
△OCA≌△ODB
O
A
B
C
D
对应角:
∠AOC和∠BOD,
∠ACO和∠BDO,
对应边:
AO和BO,
OC和OD,
CA和DB。
练一练:
3、如图,已知△ACD与△BDC全等,用符号“≌”表示这两个三角形全等,已知∠A与∠B是对应角,写出其余的对应角和对应边。
A
B
C
D
△ACD≌△BDC
对应角:
∠ADC和∠BCD,
∠ACD和∠BDC,
对应边:
AC和BD,
AD和BC
CD和DC。
全等三角形的性质
全等三角形的_________,_________。
∴
AB=DF,BC=FE,AC=DE
( )
∴
∠A=∠D,∠B=∠F
,∠C=∠E
(
)
几何语言
全等三角形的对应边相等
全等三角形的对应角相等
对应边相等
对应角相等
∵△ABC≌
△DFE
勤于巩固:
1、如图,已知△ABC≌△CDA,且AB=CD,则下列结论错误的是(
)
(A)∠1=∠2
(B)AC=CA
(C)∠D=∠B
(D)AC=BC
A
B
C
D
2
1
D
2、如图,已知△ABC≌△DEF,
△DEF的周长是32cm,DE=12cm,EF=14cm,∠E=∠B,则AC=__
A
B
C
F
E
D
6cm
勤于巩固:
3、如图,已知△ABE≌△ACF,且AB=7,AE=3则EC的长是(
)
(A)4
(B)5
(C)7
(D)3.5
F
A
B
C
E
4、如图,已知△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为_______
A
C
B
D
A
130°
概念考查:
1、下列说法,正确的是(
)
(A)形状相同的两个三角形全等;
(B)面积相等的两个三角形全等;
(C)完全重合的两个三角形全等;
(D)所有的等边三角形全等;
C
2、下列说法,正确的序号是_____________
(1)全等图形的形状相同,大小相等;
(2)全等三角形的对应边相等,对应角相等;
(3)全等三角形的周长、面积分别相等;
(1)
(2)
(3)
知识提升:
1、如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式中错误的是(
)
(A)AB=AC
(B)∠BAE=∠CAD
(C)BE=DC
(D)AD=DE
2、已知△ABC≌△DEF,BC=EF=6,△ABC的面积为18,求EF边上的高线长.
D
(没有图形时要自己构造图形)
A
B
C
D
E
1
2
知识提升:
3、如图,△ABC≌△ADE,其中点B与点D,点C与点E对应.
(1)写出对应边和对应角;
(2)∠BAD与∠CAE相等吗?请说明理由;
E
A
B
D
C
4、如图,△ABD≌△EBC,AB=3,BC=6.
(1)求DE的长;
(2)若点A、B、C在同一直线上,则DB与AC垂直吗?为什么?
A
B
C
D
E
5、如图,已知△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数
D
G
C
F
E
A
B
如图,AD平分∠BAC,AB=AC,△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由。
提示:
解:∵AD平分∠BAC,
∴∠1=∠2,
例2:
(1)如何说明两个三角形是全等三角形?
重叠
(2)如何说明两个三角形重叠呢?
三对对应点重合
因此将图形沿AD对折时,射线AB和射线AC重合。
∵AB=AC,∴点C和点B重合,
∴△ACD与△ABD重合,
∴
△ABD
≌
△ACD
∴BD=CD(……)
∠B
=∠C(……)
∴∠B=∠C(__________________).
练一练:
1.?如图,在△ABC中,AD⊥BC于点D,BD=CD.完成下面说明∠B=∠C的理由的过程(填空).
解:∵?AD⊥BC(已知),
∴∠ADB=______=Rt∠(垂直的定义).
当把图形沿AD对折时,射线DB与DC______.
∵?BD=CD(______),
∴?点B与点______重合,
∴△ABD与△ACD______,
∴△ABD______△ACD(全等三角形的定义),
A
B
C
D
1.4
全等三角形
仔细观察下列各组图形,你发现了什么?
能够重合的两个图形称为全等图形.
如果把每一对中的两个图形叠在一起,它们能重合吗?
全等图形的_______和_______完全相同。
形状
大小
下列各图形哪些是全等图形?
连一连:
思考:
(2)面积相等的两个图形是全等图形吗?
(1)全等图形的面积相等吗?
相等
不一定
(3)半径相等的两个圆是全等图形吗?
是的
(4)边长均为5cm的两个正方形是全等图形吗?
是的
F
E
D
C
B
A
能够重合的两个三角形叫做全等三角形。
全等三角形:
下面两个三角形是全等图形吗?你是怎么判断的?
“全等”用符号“≌”表示.
记作:△ABC≌△DEF
F
E
D
C
B
A
F
E
D
C
B
A
此时,能互相重合的顶点叫全等三角形的对应顶点。
能互相重合的边叫做全等三角形的对应边。
能互相重合的角叫做全等三角形的对应角。
A和D,B和E,C和F
AB和DE,AC和DF,
BC和EF
∠A和∠D,∠B和∠E,∠C和∠F
一般地,记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
△ABC≌△DEF
练一练:
1、如图,已知△OCA≌△OBD,请说出它们的对应顶点、对应边和对应角。
O
D
C
B
A
对应边:
对应顶点:
O和O。
C和B,
A和D,
CO和BO,
AO和DO,
CA和BD。
对应角:
∠A和∠D,
∠C和∠B,
∠COA和∠BOD。
练一练:
2、如图,已知△OCA与△ODB全等,用符号“≌”表示这两个三角形全等,已知∠A与∠B是对应角,写出其余的对应角和对应边。
△OCA≌△ODB
O
A
B
C
D
对应角:
∠AOC和∠BOD,
∠ACO和∠BDO,
对应边:
AO和BO,
OC和OD,
CA和DB。
练一练:
3、如图,已知△ACD与△BDC全等,用符号“≌”表示这两个三角形全等,已知∠A与∠B是对应角,写出其余的对应角和对应边。
A
B
C
D
△ACD≌△BDC
对应角:
∠ADC和∠BCD,
∠ACD和∠BDC,
对应边:
AC和BD,
AD和BC
CD和DC。
全等三角形的性质
全等三角形的_________,_________。
∴
AB=DF,BC=FE,AC=DE
( )
∴
∠A=∠D,∠B=∠F
,∠C=∠E
(
)
几何语言
全等三角形的对应边相等
全等三角形的对应角相等
对应边相等
对应角相等
∵△ABC≌
△DFE
勤于巩固:
1、如图,已知△ABC≌△CDA,且AB=CD,则下列结论错误的是(
)
(A)∠1=∠2
(B)AC=CA
(C)∠D=∠B
(D)AC=BC
A
B
C
D
2
1
D
2、如图,已知△ABC≌△DEF,
△DEF的周长是32cm,DE=12cm,EF=14cm,∠E=∠B,则AC=__
A
B
C
F
E
D
6cm
勤于巩固:
3、如图,已知△ABE≌△ACF,且AB=7,AE=3则EC的长是(
)
(A)4
(B)5
(C)7
(D)3.5
F
A
B
C
E
4、如图,已知△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为_______
A
C
B
D
A
130°
概念考查:
1、下列说法,正确的是(
)
(A)形状相同的两个三角形全等;
(B)面积相等的两个三角形全等;
(C)完全重合的两个三角形全等;
(D)所有的等边三角形全等;
C
2、下列说法,正确的序号是_____________
(1)全等图形的形状相同,大小相等;
(2)全等三角形的对应边相等,对应角相等;
(3)全等三角形的周长、面积分别相等;
(1)
(2)
(3)
知识提升:
1、如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式中错误的是(
)
(A)AB=AC
(B)∠BAE=∠CAD
(C)BE=DC
(D)AD=DE
2、已知△ABC≌△DEF,BC=EF=6,△ABC的面积为18,求EF边上的高线长.
D
(没有图形时要自己构造图形)
A
B
C
D
E
1
2
知识提升:
3、如图,△ABC≌△ADE,其中点B与点D,点C与点E对应.
(1)写出对应边和对应角;
(2)∠BAD与∠CAE相等吗?请说明理由;
E
A
B
D
C
4、如图,△ABD≌△EBC,AB=3,BC=6.
(1)求DE的长;
(2)若点A、B、C在同一直线上,则DB与AC垂直吗?为什么?
A
B
C
D
E
5、如图,已知△ABC≌△ADE,∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数
D
G
C
F
E
A
B
如图,AD平分∠BAC,AB=AC,△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由。
提示:
解:∵AD平分∠BAC,
∴∠1=∠2,
例2:
(1)如何说明两个三角形是全等三角形?
重叠
(2)如何说明两个三角形重叠呢?
三对对应点重合
因此将图形沿AD对折时,射线AB和射线AC重合。
∵AB=AC,∴点C和点B重合,
∴△ACD与△ABD重合,
∴
△ABD
≌
△ACD
∴BD=CD(……)
∠B
=∠C(……)
∴∠B=∠C(__________________).
练一练:
1.?如图,在△ABC中,AD⊥BC于点D,BD=CD.完成下面说明∠B=∠C的理由的过程(填空).
解:∵?AD⊥BC(已知),
∴∠ADB=______=Rt∠(垂直的定义).
当把图形沿AD对折时,射线DB与DC______.
∵?BD=CD(______),
∴?点B与点______重合,
∴△ABD与△ACD______,
∴△ABD______△ACD(全等三角形的定义),
A
B
C
D
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
