2020年秋浙教版浙江省宁波市国际学校八年级数学上册第4章 图形与坐标单元培优测试卷(Word版含解析)
文档属性
| 名称 | 2020年秋浙教版浙江省宁波市国际学校八年级数学上册第4章 图形与坐标单元培优测试卷(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 327.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:00:00 | ||
图片预览

文档简介
2020年秋浙教版浙江省宁波市国际学校八年级数学上册第4章
图形与坐标单元培优测试卷
一、选择题(每小题3分,共30分)
1.重庆一中寄宿学校北楼,食堂,含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示,
食堂的位置用(2,1)表示,那么含弘楼的位置表示成(??
)
A.?(0,0)???????????B.?(0,4)?????????C.?(-2,0)??????????D.?(1,5)
2.今年第4号台风“黑格比”于8月3日登陆温州,其中心位于苍南县东南方大约460公里的台湾以东洋面上,这句话中出现的下列各自然数不属于标号或排序的(??
)
A.?460????????????????????????B.?3????????????????????????????C.?4????????????????????????????D.?8
3.如图,笑脸所在的点的坐标可能是(??
)
A.?(3,2)???????????????B.?(-3,-2)??????????????C.?(-3,2)???????????????D.?(3,-2)
4.在平面直角坐标系中,点
到
轴的距离是(??
)
A.????????????????????B.????????????????????????C.????????????????????????????????D.?
5.已知点P在第四象限内,且点P到x轴的距离是3.到y轴的距离是4.那么点P的坐标是(??
)
A.?(-4,3)????????B.?(4,-3)???????????C.?(-3,4)?????????D.?(3,
-4)
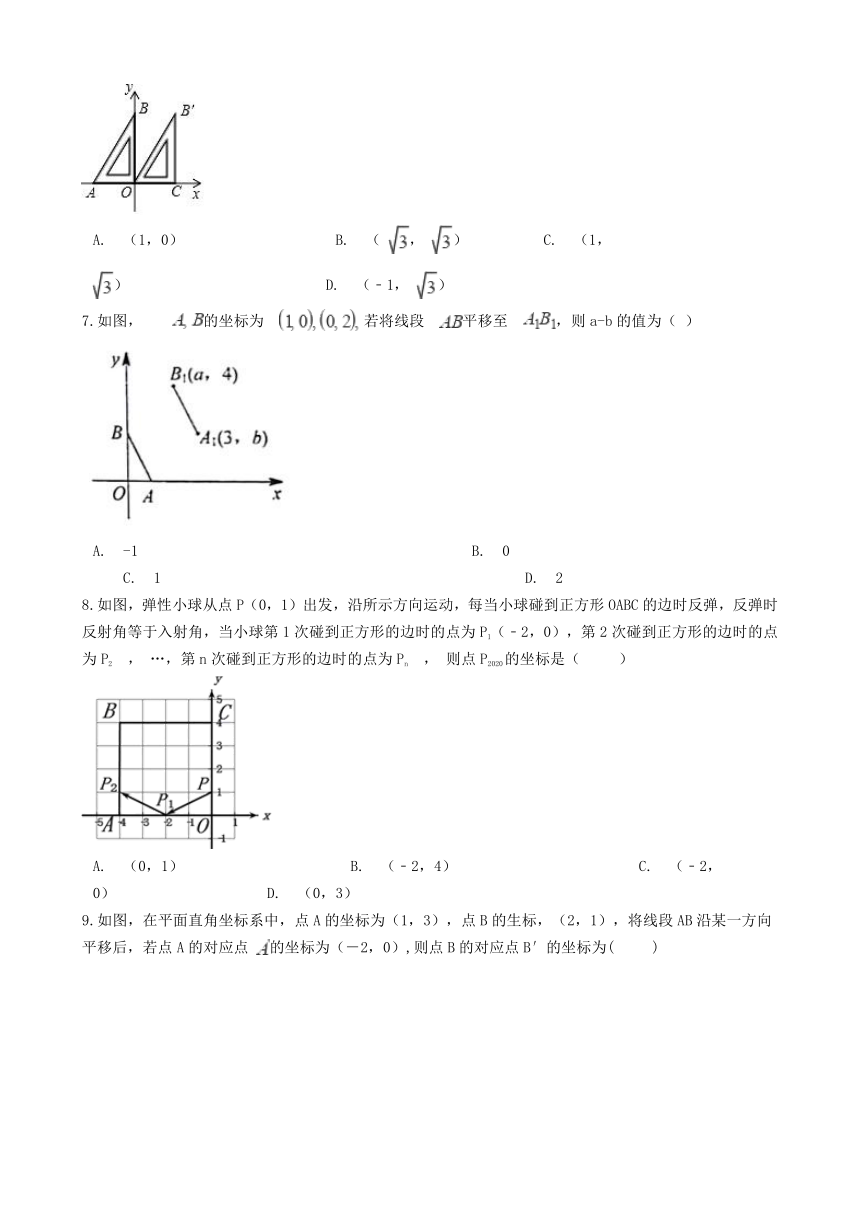
6.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,
).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(??
)
A.?(1,0)??????????B.?(
,
)?????C.?(1,
)?????????????D.?(﹣1,
)
7.如图,?
的坐标为
若将线段
平移至
,则a-b的值为(
)?
A.?-1??????????????????????B.?0???????????????????C.?1????????????????????????D.?2
8.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2
,
…,第n次碰到正方形的边时的点为Pn
,
则点P2020的坐标是(??
)
A.?(0,1)???????????B.?(﹣2,4)????????????C.?(﹣2,0)??????????D.?(0,3)
9.如图,在平面直角坐标系中,点A的坐标为(1,3),点B的生标,(2,1),将线段AB沿某一方向平移后,若点A的对应点
的坐标为(-2,0),则点B的对应点B′的坐标为(??
)
A.?(5,2)??????????B.?(-1,-2)?????????????C.?(-1,-3)????????D.?(0,-2)
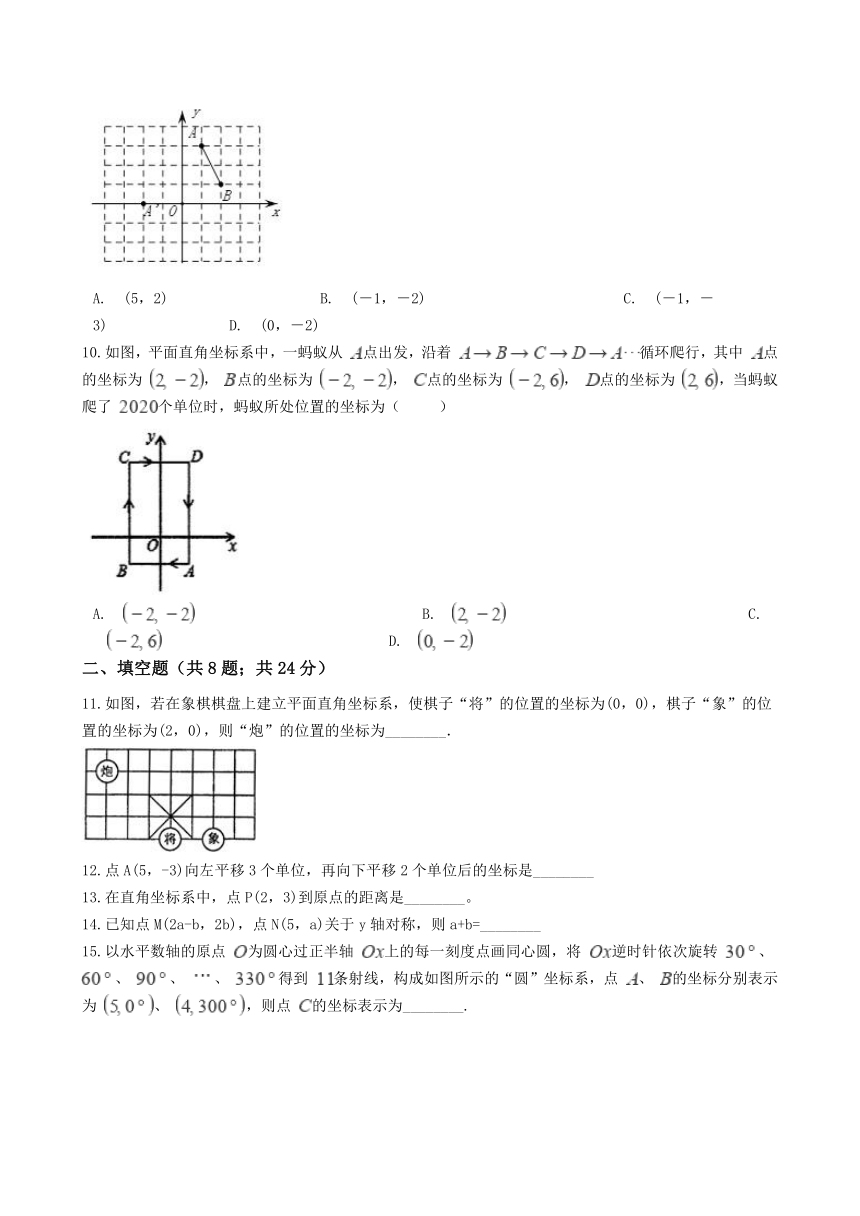
10.如图,平面直角坐标系中,一蚂蚁从
点出发,沿着
循环爬行,其中
点的坐标为
,
点的坐标为
,
点的坐标为
,
点的坐标为
,当蚂蚁爬了
个单位时,蚂蚁所处位置的坐标为(??
)
A.????????????????B.?????????????????C.????????????????D.?
二、填空题(共8题;共24分)
11.如图,若在象棋棋盘上建立平面直角坐标系,使棋子“将”的位置的坐标为(0,0),棋子“象”的位置的坐标为(2,0),则“炮”的位置的坐标为________.
12.点A(5,-3)向左平移3个单位,再向下平移2个单位后的坐标是________
13.在直角坐标系中,点P(2,3)到原点的距离是________。
14.已知点M(2a-b,2b),点N(5,a)关于y轴对称,则a+b=________
15.以水平数轴的原点
为圆心过正半轴
上的每一刻度点画同心圆,将
逆时针依次旋转
、
、
、
、
得到
条射线,构成如图所示的“圆”坐标系,点
、
的坐标分别表示为
、
,则点
的坐标表示为________.
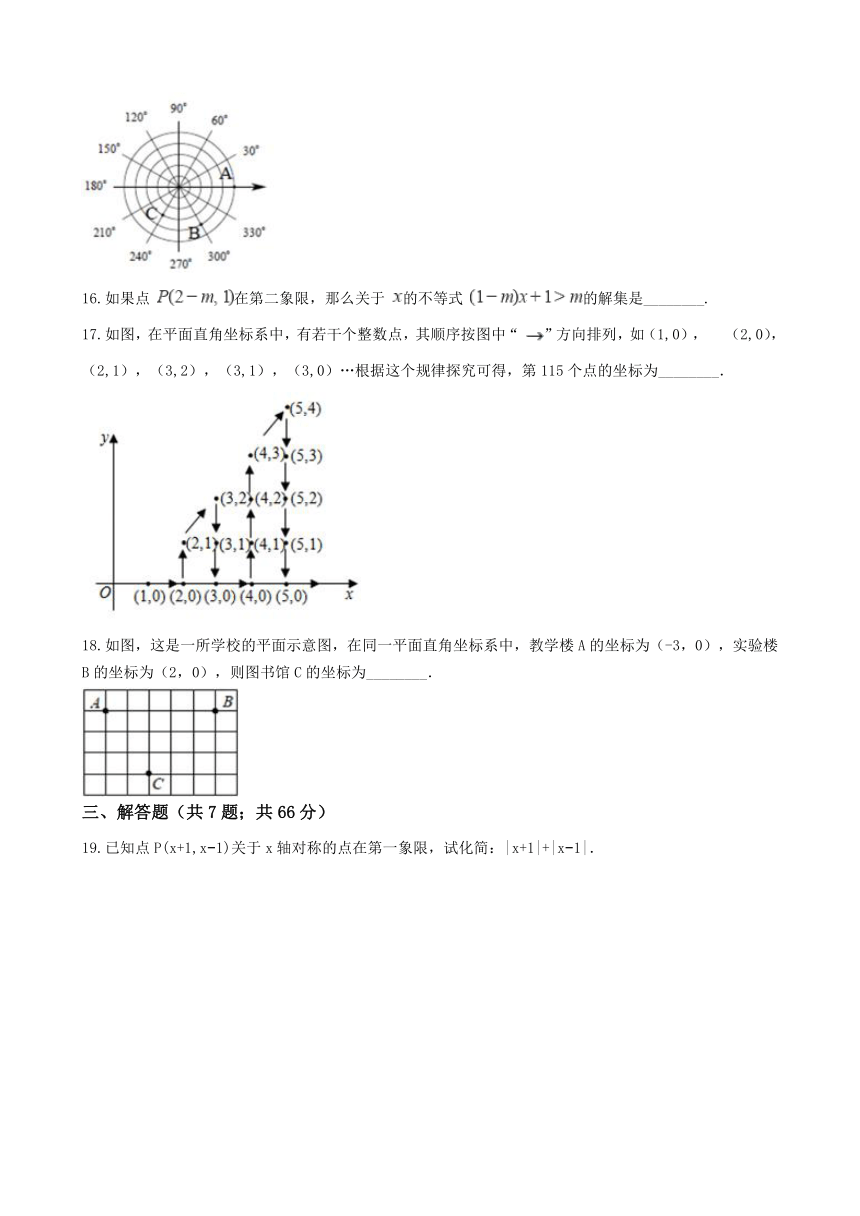
16.如果点
在第二象限,那么关于
的不等式
的解集是________.
17.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“
”方向排列,如(1,0),?
(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第115个点的坐标为________.
18.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为________.
三、解答题(共7题;共66分)
19.已知点P(x+1,x?1)关于x轴对称的点在第一象限,试化简:|x+1|+|x?1|.
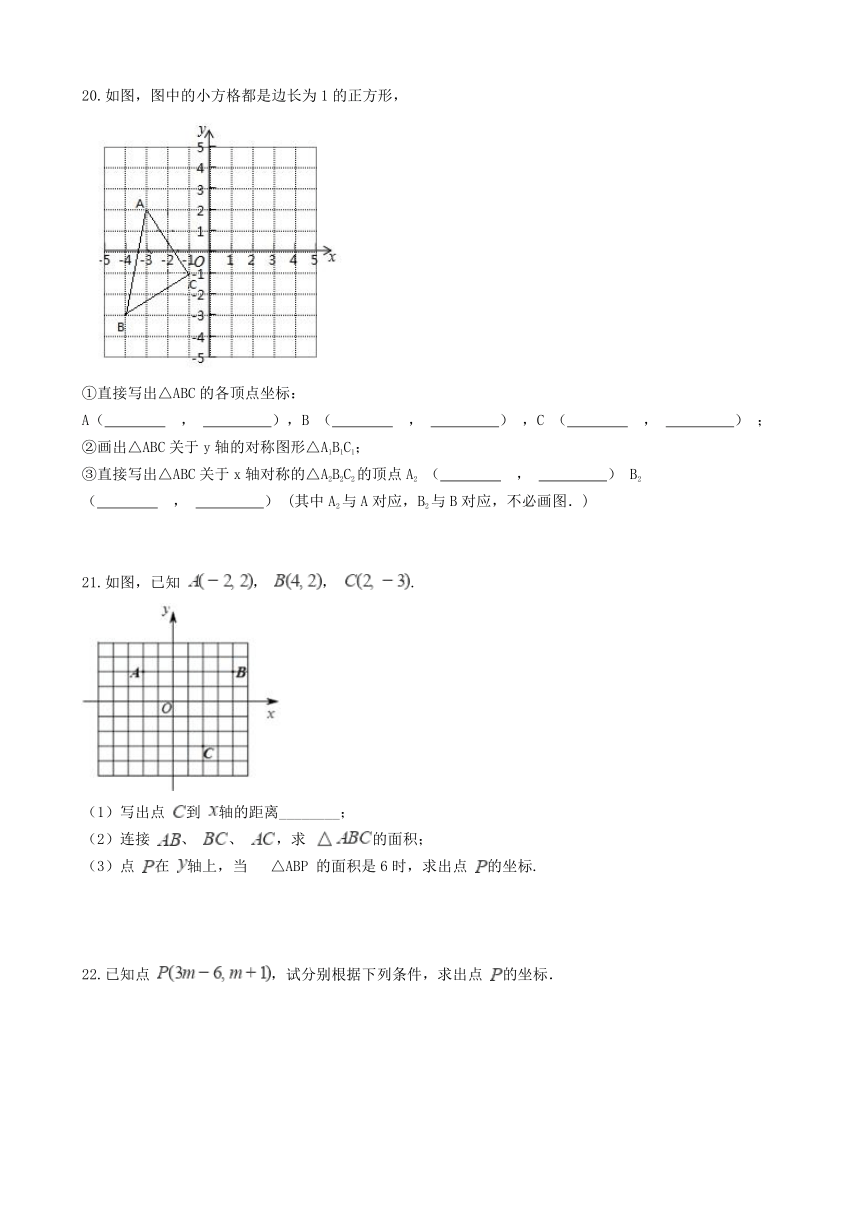
20.如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A(
???
,
????
),B
(
???
,
????
)
,C
(
???
,
????
)
;
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2
(
???
,
????
)
B2
(
???
,
????
)
(其中A2与A对应,B2与B对应,不必画图.)
21.如图,已知
,
,
.
(1)写出点
到
轴的距离________;
(2)连接
、
、
,求
的面积;
(3)点
在
轴上,当?
△ABP
的面积是6时,求出点
的坐标.
22.已知点
,试分别根据下列条件,求出点
的坐标.
(1)点
在
轴上;
(2)点
的横坐标比纵坐标大2;
(3)点
在过
,且与
轴平行的直线上.
(4)点
在到两个坐标轴的距离相等.
23.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为________,点C的坐标为________;
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3)连接AB1
,
B1C,△AB1C的面积=________.
24.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标;
(2)在x轴上是否存在点M,连接MC,MD,使
,若存在,请求出点M的坐标;若不存在,请说明理由;
(3)点P在直线BD上运动,连接PC,PO.求
的取值范围;
25.如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B方向运动,到点B停止.设点P运动的时间为t(秒).
(1)点A的坐标为________;
(2)当t=1秒时,点P的坐标________;
(3)当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);
(4)在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.
答案
一、选择题
1.由题意,坐标系的位置如图,
所以含弘楼的位置坐标为(-2,0)
故答案为:C.
2.解:A、460不属于标号或排序,符合题意;
B、3属于排序,此项不符合题意;
C、4属于标号,此项不符合题意;
D、8属于排序,此项不符合题意;
故答案为:A.
3.解:∵笑脸在第四象限,
∴横坐标大于零,纵坐标小于零,
故答案为:D.
4.解:∵点P的坐标为(-4,5),
∴点P到y轴的距离为4个单位长度.
故答案为:C.
5.解:∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0,
∵点P到x轴的距离是3,到y轴的距离是4,
∴点P的横坐标是4,纵坐标是-3,即点P的坐标为(4,-3).
故答案为:B.
6.解:因为点A与点O对应,点A(﹣1,0),点O(0,0),
所以图形向右平移1个单位长度,
所以点B的对应点B'的坐标为(0+1,
),即(1,
),
故答案为:C.
7.解:根据A(1,0)、B(0,2)、A1(3,b)、B1(a,4)可得
线段向右平移2个单位长度,向上平移两个单位长度,
则a=0+2=2,b=0+2=2,
所以a-b=2-2=0.
故答案为:B.
8.解:如图,
根据反射角等于入射角画图,可知光线从P2反射后到P3(0,3),再反射到P4(-2,4),再反射到P5(-4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,2020÷6=336……4,即点P2020的坐标是(-2,4),
故答案为:B.
9.解:因为点A(1,3)平移到点
(-2,0),横坐标减3,纵坐标减3,
故点B(2,1)平移到点B′横、纵坐标也都减3,
所以B′的坐标为(-1,-2).
故答案为:B
10解:∵A点坐标为(2,﹣2),B点坐标为(﹣2,﹣2),C点坐标为(﹣2,6),
∴AB=2﹣(﹣2)=4,BC=6﹣(﹣2)=8,
∴从A→B→C→D→A一圈的长度为2(AB+BC)=24.
∵2020=84×24+4,
∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即(-2,﹣2).
故答案为:A
二、填空题
11.解:∵棋子将所在位置的坐标为(0,0),棋子“象”的位置的坐标为(2,0),可以确定坐标系,
∴确定原点在将的位置,且一个棋格为一个单位长度,
∴棋子炮所在的位置的坐标为
;
故答案为
.
12.解:
点A(5,-3)向左平移3个单位,再向下平移2个单位后的坐标是(5-2,-3-2)?,
即(2,-5).
故答案为:
(2,-5)
.
13.解:∵点P(2,3)到x轴的距离为3,到y轴的距离为2,
∴
点P(2,3)到原点的距离=.
故答案为:.
14.解:由题意,得
2a-b+5=0,2b=a,
解得b=
,a=
.
a+b=-5,
故答案为:-5.
15.解:图中为5个同心圆,且每条射线与x轴所形成的角度已知,
、
的坐标分别表示为
、
,根据点的特征,所以点
的坐标表示为
;
故答案为:
.
16.∵点
在第二象限,
∴
,
解得
,
∴
.
∵
,
∴
,
故答案为:
.
17.解:∵横坐标为1的点只有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标分别为0,1;
横坐标为3的点有3个,纵坐标分别为0,1,2
横坐标为4的点有4个,纵坐标分别为0,1,2,3
偶数行箭头向上,奇数行箭头向下;
1+2+3++14=105.
∵偶数列箭头向上,第105个点的坐标为(14,13)
∵115-10=105
∵奇函数列的箭头向下,
∴第115个点的横坐标为15,纵坐标为14-10+1=5‘’
∴第115个点为:(15,5).
故答案为:(15,5).
18.解:如图所示:
图书馆C的坐标为(-1,-3).
故答案为:(-1,-3).
三、解答题
19.
解:∵点p(x+1,
x-1)关于x轴对称的点在第一象限
∴点P在第四象限
∴x+1
>0,x-1<0
∴|
x+1
|+|
x-1
|=(x+1)-(
x-1)=
2
20.
解:①△ABC的各顶点坐标:A(﹣3,2)、B(﹣4,﹣3)、C(﹣1,﹣1);
故答案为:﹣3、2;﹣4、﹣3;﹣1、﹣1;
②如图,△A1B1C1即为所求,
③如图,△A2B2C2即为所求,A2坐标为(﹣3,﹣2)、B2坐标为(﹣4,3).
故答案为:﹣3、﹣2;﹣4、3.
21.
(1)3
(2)解:如图,
(3)解:设点P的坐标为(0,b),
则点P到AB的距离为
,AB=6
S△ABP=
=6解得b=0或b=4
∴点P的坐标为(0,0)或(0,4)
解:(1)∵C(2,-3),
∴点C到x轴的距离是3,
故答案为:3.
22.
(1)∵点
在
轴上,
∴点
的横坐标为0,
即
,解得
,
则
.
(2)∵点
的横坐标比纵坐标大2,
∴
,解得
,
则
.
(3)∵点
在过
,且与
轴平行的直线上,
∴点
的纵坐标等于
,
即
,解得
,
则
.
(4)∵点
到两个坐标轴的距离相等,
∴
或
,
解得
或
,
则
或
.
23.
(1)(2,7);(6,5)
(2)解:△A1B1C1如图所示
(3)21
(3)解:△AB1C的面积=9×8﹣
×8×5﹣
×9×6﹣
×2×4,
=72﹣20﹣27﹣4,
=72﹣51,
=21.
24.
(1)由平移知,点C(0,2),D(4,2);
(2)存在,理由:由平移知,CD∥AB,
由(1)知,C(0,2),D(4,2),
∴CD=4,
设点M(m,0),
∵B(3,0),
∴BM=|m-3|
∵S△MDC=2S△MBD
,
∴
CD×2=2×
BM×2,
∴CD=2BM,
∴4=2|m-3|,
∴m=5或m=1,
∴M(5,0)或(1,0);
(3)方法1、由(1)知,D(4,2),
设直线BD的解析式为y=kx+b,
,
∴
,
∴直线BD
的解析式为y=2x-6,
设P(n,2n-6),
当点P在线段BD上时,即3≤n≤4,
S△CDP+S△BOP=
OB×yP+
CD×(2-yP)
=
[3(2n-6)+4(2-2n+6)]
=
(-2n-2)
=-n+7,
∴3≤S△CDP+S△BOP≤4,
当点P在射线DB上时,即n<3,
S△CDP+S△BOP=
OB×(-yP)+
CD×(2-yP)
=
[3(6-2n)+4(2-2n+6)]
=
(-14n+50)
=-7n+25,
∴S△CDP+S△BOP>4,
当点P在射线BD上时,即n>4,
S△CDP+S△BOP=
OB×yP+
CD×(yP-2)
=
[3(2n-6)+4(2n-6-2)]
=
(14n-50)=7n-25,
∴S△CDP+S△BOP>3,
即S△CDP+S△BOP>3.
方法2、如图,
设点P的坐标为(m,n),
∵C(0,2),D(4,2),B(3,0),
∴OC=2,CD=4,OB=3,
∴S△CDP+S△BOP=
×4×|n-2|+
×3×|n|,
当n>2时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=
n-4>3,
当0≤n≤2时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=4-
n,
∴3≤S△CDP+S△BOP≤4,
当n<0时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=4-
n>4,
即:S△CDP+S△BOP>3.
25.
(1)(4,0)
(2)(0,2)
(3)当点P在OC上运动,
(4)当点P到y轴的距离为1个单位长度时,此时P在CB上,
的运动路程
解:(1)
长方形OABC,B坐标为(4,6),
?
故答案为:(4,0).(2)当
时,
此时P在y轴上,
,
故答案为:(0,2);
图形与坐标单元培优测试卷
一、选择题(每小题3分,共30分)
1.重庆一中寄宿学校北楼,食堂,含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示,
食堂的位置用(2,1)表示,那么含弘楼的位置表示成(??
)
A.?(0,0)???????????B.?(0,4)?????????C.?(-2,0)??????????D.?(1,5)
2.今年第4号台风“黑格比”于8月3日登陆温州,其中心位于苍南县东南方大约460公里的台湾以东洋面上,这句话中出现的下列各自然数不属于标号或排序的(??
)
A.?460????????????????????????B.?3????????????????????????????C.?4????????????????????????????D.?8
3.如图,笑脸所在的点的坐标可能是(??
)
A.?(3,2)???????????????B.?(-3,-2)??????????????C.?(-3,2)???????????????D.?(3,-2)
4.在平面直角坐标系中,点
到
轴的距离是(??
)
A.????????????????????B.????????????????????????C.????????????????????????????????D.?
5.已知点P在第四象限内,且点P到x轴的距离是3.到y轴的距离是4.那么点P的坐标是(??
)
A.?(-4,3)????????B.?(4,-3)???????????C.?(-3,4)?????????D.?(3,
-4)
6.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,
).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(??
)
A.?(1,0)??????????B.?(
,
)?????C.?(1,
)?????????????D.?(﹣1,
)
7.如图,?
的坐标为
若将线段
平移至
,则a-b的值为(
)?
A.?-1??????????????????????B.?0???????????????????C.?1????????????????????????D.?2
8.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(﹣2,0),第2次碰到正方形的边时的点为P2
,
…,第n次碰到正方形的边时的点为Pn
,
则点P2020的坐标是(??
)
A.?(0,1)???????????B.?(﹣2,4)????????????C.?(﹣2,0)??????????D.?(0,3)
9.如图,在平面直角坐标系中,点A的坐标为(1,3),点B的生标,(2,1),将线段AB沿某一方向平移后,若点A的对应点
的坐标为(-2,0),则点B的对应点B′的坐标为(??
)
A.?(5,2)??????????B.?(-1,-2)?????????????C.?(-1,-3)????????D.?(0,-2)
10.如图,平面直角坐标系中,一蚂蚁从
点出发,沿着
循环爬行,其中
点的坐标为
,
点的坐标为
,
点的坐标为
,
点的坐标为
,当蚂蚁爬了
个单位时,蚂蚁所处位置的坐标为(??
)
A.????????????????B.?????????????????C.????????????????D.?
二、填空题(共8题;共24分)
11.如图,若在象棋棋盘上建立平面直角坐标系,使棋子“将”的位置的坐标为(0,0),棋子“象”的位置的坐标为(2,0),则“炮”的位置的坐标为________.
12.点A(5,-3)向左平移3个单位,再向下平移2个单位后的坐标是________
13.在直角坐标系中,点P(2,3)到原点的距离是________。
14.已知点M(2a-b,2b),点N(5,a)关于y轴对称,则a+b=________
15.以水平数轴的原点
为圆心过正半轴
上的每一刻度点画同心圆,将
逆时针依次旋转
、
、
、
、
得到
条射线,构成如图所示的“圆”坐标系,点
、
的坐标分别表示为
、
,则点
的坐标表示为________.
16.如果点
在第二象限,那么关于
的不等式
的解集是________.
17.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“
”方向排列,如(1,0),?
(2,0),(2,1),(3,2),(3,1),(3,0)…根据这个规律探究可得,第115个点的坐标为________.
18.如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(-3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为________.
三、解答题(共7题;共66分)
19.已知点P(x+1,x?1)关于x轴对称的点在第一象限,试化简:|x+1|+|x?1|.
20.如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A(
???
,
????
),B
(
???
,
????
)
,C
(
???
,
????
)
;
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2
(
???
,
????
)
B2
(
???
,
????
)
(其中A2与A对应,B2与B对应,不必画图.)
21.如图,已知
,
,
.
(1)写出点
到
轴的距离________;
(2)连接
、
、
,求
的面积;
(3)点
在
轴上,当?
△ABP
的面积是6时,求出点
的坐标.
22.已知点
,试分别根据下列条件,求出点
的坐标.
(1)点
在
轴上;
(2)点
的横坐标比纵坐标大2;
(3)点
在过
,且与
轴平行的直线上.
(4)点
在到两个坐标轴的距离相等.
23.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为________,点C的坐标为________;
(2)将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3)连接AB1
,
B1C,△AB1C的面积=________.
24.如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标;
(2)在x轴上是否存在点M,连接MC,MD,使
,若存在,请求出点M的坐标;若不存在,请说明理由;
(3)点P在直线BD上运动,连接PC,PO.求
的取值范围;
25.如图,在长方形OABC中,O为平面直角坐标系的原点,点A,点C分别在x轴,y轴上,点B坐标为(4,6),点P从点O出发,以每秒2个单位长度的速度沿O→C→B方向运动,到点B停止.设点P运动的时间为t(秒).
(1)点A的坐标为________;
(2)当t=1秒时,点P的坐标________;
(3)当点P在OC上运动,请直接写出点P的坐标(用含有t的式子表示);
(4)在移动过程中,当点P到y轴的距离为1个单位长度时,求t的值.
答案
一、选择题
1.由题意,坐标系的位置如图,
所以含弘楼的位置坐标为(-2,0)
故答案为:C.
2.解:A、460不属于标号或排序,符合题意;
B、3属于排序,此项不符合题意;
C、4属于标号,此项不符合题意;
D、8属于排序,此项不符合题意;
故答案为:A.
3.解:∵笑脸在第四象限,
∴横坐标大于零,纵坐标小于零,
故答案为:D.
4.解:∵点P的坐标为(-4,5),
∴点P到y轴的距离为4个单位长度.
故答案为:C.
5.解:∵点P在第四象限内,
∴点P的横坐标大于0,纵坐标小于0,
∵点P到x轴的距离是3,到y轴的距离是4,
∴点P的横坐标是4,纵坐标是-3,即点P的坐标为(4,-3).
故答案为:B.
6.解:因为点A与点O对应,点A(﹣1,0),点O(0,0),
所以图形向右平移1个单位长度,
所以点B的对应点B'的坐标为(0+1,
),即(1,
),
故答案为:C.
7.解:根据A(1,0)、B(0,2)、A1(3,b)、B1(a,4)可得
线段向右平移2个单位长度,向上平移两个单位长度,
则a=0+2=2,b=0+2=2,
所以a-b=2-2=0.
故答案为:B.
8.解:如图,
根据反射角等于入射角画图,可知光线从P2反射后到P3(0,3),再反射到P4(-2,4),再反射到P5(-4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,2020÷6=336……4,即点P2020的坐标是(-2,4),
故答案为:B.
9.解:因为点A(1,3)平移到点
(-2,0),横坐标减3,纵坐标减3,
故点B(2,1)平移到点B′横、纵坐标也都减3,
所以B′的坐标为(-1,-2).
故答案为:B
10解:∵A点坐标为(2,﹣2),B点坐标为(﹣2,﹣2),C点坐标为(﹣2,6),
∴AB=2﹣(﹣2)=4,BC=6﹣(﹣2)=8,
∴从A→B→C→D→A一圈的长度为2(AB+BC)=24.
∵2020=84×24+4,
∴当蚂蚁爬了2020个单位时,它所处位置在点A左边4个单位长度处,即(-2,﹣2).
故答案为:A
二、填空题
11.解:∵棋子将所在位置的坐标为(0,0),棋子“象”的位置的坐标为(2,0),可以确定坐标系,
∴确定原点在将的位置,且一个棋格为一个单位长度,
∴棋子炮所在的位置的坐标为
;
故答案为
.
12.解:
点A(5,-3)向左平移3个单位,再向下平移2个单位后的坐标是(5-2,-3-2)?,
即(2,-5).
故答案为:
(2,-5)
.
13.解:∵点P(2,3)到x轴的距离为3,到y轴的距离为2,
∴
点P(2,3)到原点的距离=.
故答案为:.
14.解:由题意,得
2a-b+5=0,2b=a,
解得b=
,a=
.
a+b=-5,
故答案为:-5.
15.解:图中为5个同心圆,且每条射线与x轴所形成的角度已知,
、
的坐标分别表示为
、
,根据点的特征,所以点
的坐标表示为
;
故答案为:
.
16.∵点
在第二象限,
∴
,
解得
,
∴
.
∵
,
∴
,
故答案为:
.
17.解:∵横坐标为1的点只有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标分别为0,1;
横坐标为3的点有3个,纵坐标分别为0,1,2
横坐标为4的点有4个,纵坐标分别为0,1,2,3
偶数行箭头向上,奇数行箭头向下;
1+2+3++14=105.
∵偶数列箭头向上,第105个点的坐标为(14,13)
∵115-10=105
∵奇函数列的箭头向下,
∴第115个点的横坐标为15,纵坐标为14-10+1=5‘’
∴第115个点为:(15,5).
故答案为:(15,5).
18.解:如图所示:
图书馆C的坐标为(-1,-3).
故答案为:(-1,-3).
三、解答题
19.
解:∵点p(x+1,
x-1)关于x轴对称的点在第一象限
∴点P在第四象限
∴x+1
>0,x-1<0
∴|
x+1
|+|
x-1
|=(x+1)-(
x-1)=
2
20.
解:①△ABC的各顶点坐标:A(﹣3,2)、B(﹣4,﹣3)、C(﹣1,﹣1);
故答案为:﹣3、2;﹣4、﹣3;﹣1、﹣1;
②如图,△A1B1C1即为所求,
③如图,△A2B2C2即为所求,A2坐标为(﹣3,﹣2)、B2坐标为(﹣4,3).
故答案为:﹣3、﹣2;﹣4、3.
21.
(1)3
(2)解:如图,
(3)解:设点P的坐标为(0,b),
则点P到AB的距离为
,AB=6
S△ABP=
=6解得b=0或b=4
∴点P的坐标为(0,0)或(0,4)
解:(1)∵C(2,-3),
∴点C到x轴的距离是3,
故答案为:3.
22.
(1)∵点
在
轴上,
∴点
的横坐标为0,
即
,解得
,
则
.
(2)∵点
的横坐标比纵坐标大2,
∴
,解得
,
则
.
(3)∵点
在过
,且与
轴平行的直线上,
∴点
的纵坐标等于
,
即
,解得
,
则
.
(4)∵点
到两个坐标轴的距离相等,
∴
或
,
解得
或
,
则
或
.
23.
(1)(2,7);(6,5)
(2)解:△A1B1C1如图所示
(3)21
(3)解:△AB1C的面积=9×8﹣
×8×5﹣
×9×6﹣
×2×4,
=72﹣20﹣27﹣4,
=72﹣51,
=21.
24.
(1)由平移知,点C(0,2),D(4,2);
(2)存在,理由:由平移知,CD∥AB,
由(1)知,C(0,2),D(4,2),
∴CD=4,
设点M(m,0),
∵B(3,0),
∴BM=|m-3|
∵S△MDC=2S△MBD
,
∴
CD×2=2×
BM×2,
∴CD=2BM,
∴4=2|m-3|,
∴m=5或m=1,
∴M(5,0)或(1,0);
(3)方法1、由(1)知,D(4,2),
设直线BD的解析式为y=kx+b,
,
∴
,
∴直线BD
的解析式为y=2x-6,
设P(n,2n-6),
当点P在线段BD上时,即3≤n≤4,
S△CDP+S△BOP=
OB×yP+
CD×(2-yP)
=
[3(2n-6)+4(2-2n+6)]
=
(-2n-2)
=-n+7,
∴3≤S△CDP+S△BOP≤4,
当点P在射线DB上时,即n<3,
S△CDP+S△BOP=
OB×(-yP)+
CD×(2-yP)
=
[3(6-2n)+4(2-2n+6)]
=
(-14n+50)
=-7n+25,
∴S△CDP+S△BOP>4,
当点P在射线BD上时,即n>4,
S△CDP+S△BOP=
OB×yP+
CD×(yP-2)
=
[3(2n-6)+4(2n-6-2)]
=
(14n-50)=7n-25,
∴S△CDP+S△BOP>3,
即S△CDP+S△BOP>3.
方法2、如图,
设点P的坐标为(m,n),
∵C(0,2),D(4,2),B(3,0),
∴OC=2,CD=4,OB=3,
∴S△CDP+S△BOP=
×4×|n-2|+
×3×|n|,
当n>2时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=
n-4>3,
当0≤n≤2时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=4-
n,
∴3≤S△CDP+S△BOP≤4,
当n<0时,S△CDP+S△BOP=
×4×|n-2|+
×3×|n|=4-
n>4,
即:S△CDP+S△BOP>3.
25.
(1)(4,0)
(2)(0,2)
(3)当点P在OC上运动,
(4)当点P到y轴的距离为1个单位长度时,此时P在CB上,
的运动路程
解:(1)
长方形OABC,B坐标为(4,6),
?
故答案为:(4,0).(2)当
时,
此时P在y轴上,
,
故答案为:(0,2);
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
