浙教版九年级上册数学第三章圆的基本性质单元测试卷(Word版 含答案)
文档属性
| 名称 | 浙教版九年级上册数学第三章圆的基本性质单元测试卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 138.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-24 00:08:52 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2020学年浙教版九上数学第三章单元测试卷(无答案)
一、单选题
1.在半径为3的⊙O中,弦AB=3,则的长为(?)
A.
B.π或5π
C.π
D.2π
2.若扇形的半径为4,圆心角为90°,则此扇形的弧长是( ??)
A.π
B.2π
C.4π
D.8π
3.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(???)
A.第①块
B.第②块
C.第③块
D.第④块
4.可以作圆,且只可以作一个圆的条件是(??
)
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一直线上的三点
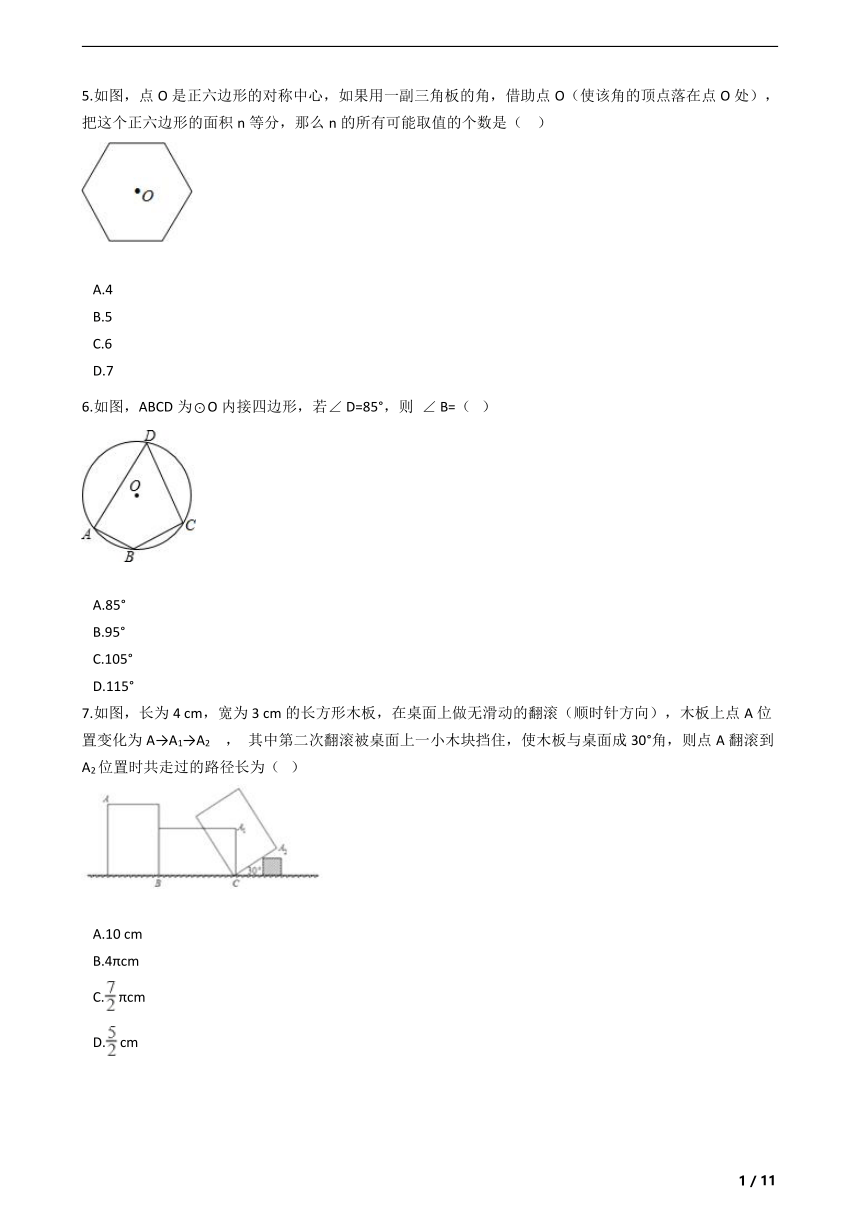
5.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是(??
)
A.4
B.5
C.6
D.7
6.如图,ABCD为⊙O内接四边形,若∠
D=85°,则
∠
B=(???)
A.85°
B.95°
C.105°
D.115°
7.如图,长为4
cm,宽为3
cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2
,
其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为(???)
A.10
cm
B.4πcm
C.πcm
D.cm
8.下列命题中是假命题的是(?
)
A.直径是弦;
B.等弧所在的圆是同圆或等圆
C.弦的垂直平分线经过圆心;
D.平分弦的直径垂直于弦
9.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心(???)
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
10.在平面直角坐标系中,⊙
P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被OP所截的弦AB的长为2,
则a的值是(???
)
A.2
B.2+
C.2
D.2+
二、填空题
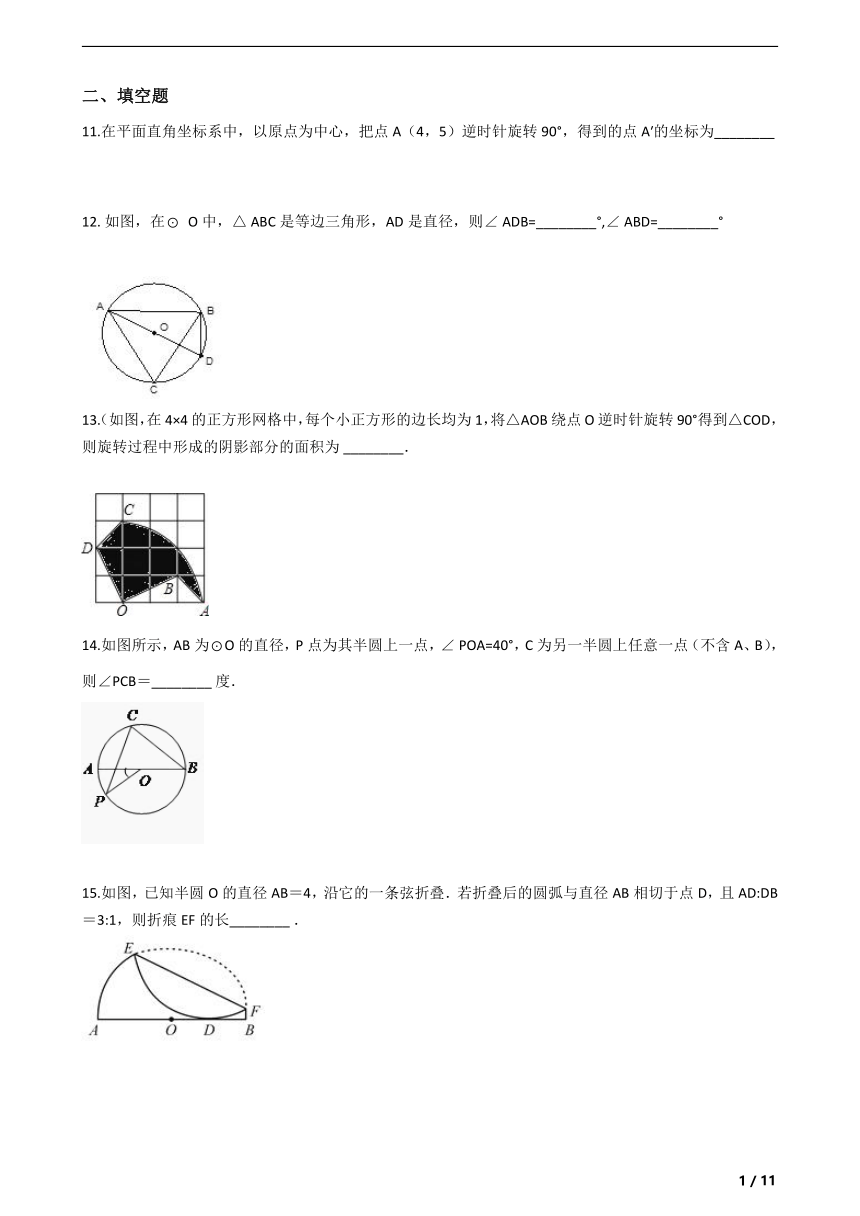
11.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为________?
12.?如图,在⊙
O中,△
ABC是等边三角形,AD是直径,则∠
ADB=________°,∠
ABD=________°
13.(如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为?________.
14.如图所示,AB为⊙O的直径,P点为其半圆上一点,∠
POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB=________?度.
15.如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长________?.
16.如图,⊙
O是△ABC的外接圆,∠
OBC=30°,则∠
BAC的度数为________?。
17.如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为________(用含a的代数式表示,结果保留π).
18.如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥
AD于E,连接BE,在点D移动的过程中,BE的取值范围是________.
三、解答题
19.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,求弧AD的长
20.如图,在△
ABC中,∠
CAB=70°,在同一平面内,将△
ABC绕点A旋转到△
AB′C′的位置,使得CC′∥
AB
,
求∠
BAB′的度数.
21.如图所示,已知正方形ABCD中的△
DCF可以经过旋转得到△
BCE
.
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
22.如图,正方形ABCD的外接圆为⊙
O,点P在劣弧
上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙
O的半径为8,求正方形ABCD的边长.
23.如图,AB是⊙
O的直径,直线CD与⊙
O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
(1)求证:AD⊥
CD;
(2)若∠
CAD=30°.⊙
O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,
≈1.73,结果保留一位小数.)
24.如图,⊙
O是△
ABC的外接圆,AB是⊙
O的直径,FO⊥
AB,垂足为点O,连接AF并延长交⊙
O于点D,连接OD交BC于点E,∠B=30°,FO=.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
答案部分
第
1
题:
【答案】
B
第
2
题:
【答案】
B
第
3
题:
【答案】
B
第
4
题:
【答案】
D
第
5
题:
【答案】
B
第
6
题:
【答案】
B
第
7
题:
【答案】
C
第
8
题:
【答案】
D
第
9
题:
【答案】
D
第
10
题:
【答案】
B
第
11
题:
【答案】
(﹣5,4)
第
12
题:
【答案】
60;90
第
13
题:
【答案】
第
14
题:
【答案】
70
第
15
题:
【答案】
________
第
16
题:
【答案】
60°
第
17
题:
【答案】
(πa2﹣2a2)
第
18
题:
【答案】
﹣2≤BE<3
第
19
题:
【答案】
解:∵在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,
∴AB=2BC=2,∠ABC=90°-∠BAC=60°,
∴∠ABD=180°-∠ABC=120°,
∴弧AD=
故答案为
.
第
20
题:
【答案】
【解答】∵CC′∥AB
,
∴∠A
CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
第
21
题:
【答案】
【解答】①△DCF绕点C逆时针旋转得到△BCE
,
所以旋转中心为点C;
②∵四边形ABCD为正方形,
∴CB=CD
,
∠BCD=90°,
∴△DCF绕点C逆时针旋转90°得到△BCE;
③∵△DCF绕点C逆时针旋转90°得到△BCE
,
∴CE=CF
,
∠ECF=90°,连接EF
∴△CEF为等腰直角三角形,
∴EF=CF=cm.
第
22
题:
【答案】
(1)解:连接OB,OC,∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC=
∠BOC=45°;
(2)解:过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2
,
∴BE=
?∴BC=2BE=2×
第
23
题:
【答案】
(1)解:连接OC.
∵直线CD与⊙
O相切,
∴OC⊥CD.
∵点C是
的中点,
∴∠DAC=∠EAC.
∵OA=OC,∴∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴AD⊥CD.
(2)解:∵∠CAD=30°,
∴∠CAE=∠CAD=30°,由圆周角定理得:∠COE=60°,
∴OE=2OC=6,EC=
OC=3
,
=
=π,
∴蚂蚁爬过的路程=3+3
+π≈11.3.
第
24
题:
【答案】
解:(1)∵OF⊥AB,
∴∠BOF=90°,
∵∠B=30°,FO=,
∴OB=6,AB=2OB=12,
又∵AB为⊙
O的直径,
∴∠ACB=90°,
∴AC=AB=6;
(2)∵由(1)可知,AB=12,
∴AO=6,即AC=AO,
在Rt△ACF和Rt△AOF中,
∴Rt△ACF≌Rt△AOF,
∴∠FAO=∠FAC=30°,
∴∠DOB=60°,
过点D作DG⊥AB于点G,
∵OD=6,∴DG=,
∴S△ACF+S△OFD=S△AOD=×6×3=9,
即阴影部分的面积是9.
1
/
12
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
2020学年浙教版九上数学第三章单元测试卷(无答案)
一、单选题
1.在半径为3的⊙O中,弦AB=3,则的长为(?)
A.
B.π或5π
C.π
D.2π
2.若扇形的半径为4,圆心角为90°,则此扇形的弧长是( ??)
A.π
B.2π
C.4π
D.8π
3.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(???)
A.第①块
B.第②块
C.第③块
D.第④块
4.可以作圆,且只可以作一个圆的条件是(??
)
A.已知圆心
B.已知半径
C.过三个已知点
D.过不在同一直线上的三点
5.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使该角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是(??
)
A.4
B.5
C.6
D.7
6.如图,ABCD为⊙O内接四边形,若∠
D=85°,则
∠
B=(???)
A.85°
B.95°
C.105°
D.115°
7.如图,长为4
cm,宽为3
cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2
,
其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为(???)
A.10
cm
B.4πcm
C.πcm
D.cm
8.下列命题中是假命题的是(?
)
A.直径是弦;
B.等弧所在的圆是同圆或等圆
C.弦的垂直平分线经过圆心;
D.平分弦的直径垂直于弦
9.同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,如图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以点A为中心(???)
A.顺时针旋转60°得到
B.顺时针旋转120°得到
C.逆时针旋转60°得到
D.逆时针旋转120°得到
10.在平面直角坐标系中,⊙
P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被OP所截的弦AB的长为2,
则a的值是(???
)
A.2
B.2+
C.2
D.2+
二、填空题
11.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为________?
12.?如图,在⊙
O中,△
ABC是等边三角形,AD是直径,则∠
ADB=________°,∠
ABD=________°
13.(如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为?________.
14.如图所示,AB为⊙O的直径,P点为其半圆上一点,∠
POA=40°,C为另一半圆上任意一点(不含A、B),则∠PCB=________?度.
15.如图,已知半圆O的直径AB=4,沿它的一条弦折叠.若折叠后的圆弧与直径AB相切于点D,且AD:DB=3:1,则折痕EF的长________?.
16.如图,⊙
O是△ABC的外接圆,∠
OBC=30°,则∠
BAC的度数为________?。
17.如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为________(用含a的代数式表示,结果保留π).
18.如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥
AD于E,连接BE,在点D移动的过程中,BE的取值范围是________.
三、解答题
19.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,求弧AD的长
20.如图,在△
ABC中,∠
CAB=70°,在同一平面内,将△
ABC绕点A旋转到△
AB′C′的位置,使得CC′∥
AB
,
求∠
BAB′的度数.
21.如图所示,已知正方形ABCD中的△
DCF可以经过旋转得到△
BCE
.
①图中哪一个点是旋转中心?
②按什么方向旋转了多少度?
③如果CF=3cm.求EF的长?
22.如图,正方形ABCD的外接圆为⊙
O,点P在劣弧
上(不与C点重合).
(1)求∠BPC的度数;
(2)若⊙
O的半径为8,求正方形ABCD的边长.
23.如图,AB是⊙
O的直径,直线CD与⊙
O相切于点C,且与AB的延长线交于点E.点C是弧BF的中点.
(1)求证:AD⊥
CD;
(2)若∠
CAD=30°.⊙
O的半径为3,一只蚂蚁从点B出发,沿着BE--EC--弧CB爬回至点B,求蚂蚁爬过的路程(π≈3.14,
≈1.73,结果保留一位小数.)
24.如图,⊙
O是△
ABC的外接圆,AB是⊙
O的直径,FO⊥
AB,垂足为点O,连接AF并延长交⊙
O于点D,连接OD交BC于点E,∠B=30°,FO=.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
答案部分
第
1
题:
【答案】
B
第
2
题:
【答案】
B
第
3
题:
【答案】
B
第
4
题:
【答案】
D
第
5
题:
【答案】
B
第
6
题:
【答案】
B
第
7
题:
【答案】
C
第
8
题:
【答案】
D
第
9
题:
【答案】
D
第
10
题:
【答案】
B
第
11
题:
【答案】
(﹣5,4)
第
12
题:
【答案】
60;90
第
13
题:
【答案】
第
14
题:
【答案】
70
第
15
题:
【答案】
________
第
16
题:
【答案】
60°
第
17
题:
【答案】
(πa2﹣2a2)
第
18
题:
【答案】
﹣2≤BE<3
第
19
题:
【答案】
解:∵在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,
∴AB=2BC=2,∠ABC=90°-∠BAC=60°,
∴∠ABD=180°-∠ABC=120°,
∴弧AD=
故答案为
.
第
20
题:
【答案】
【解答】∵CC′∥AB
,
∴∠A
CC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠AC′C=70°,
∴∠CAC′=180°-70°-70°=40°,
∴∠BAB′=40°.
第
21
题:
【答案】
【解答】①△DCF绕点C逆时针旋转得到△BCE
,
所以旋转中心为点C;
②∵四边形ABCD为正方形,
∴CB=CD
,
∠BCD=90°,
∴△DCF绕点C逆时针旋转90°得到△BCE;
③∵△DCF绕点C逆时针旋转90°得到△BCE
,
∴CE=CF
,
∠ECF=90°,连接EF
∴△CEF为等腰直角三角形,
∴EF=CF=cm.
第
22
题:
【答案】
(1)解:连接OB,OC,∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC=
∠BOC=45°;
(2)解:过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2
,
∴BE=
?∴BC=2BE=2×
第
23
题:
【答案】
(1)解:连接OC.
∵直线CD与⊙
O相切,
∴OC⊥CD.
∵点C是
的中点,
∴∠DAC=∠EAC.
∵OA=OC,∴∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∴AD⊥CD.
(2)解:∵∠CAD=30°,
∴∠CAE=∠CAD=30°,由圆周角定理得:∠COE=60°,
∴OE=2OC=6,EC=
OC=3
,
=
=π,
∴蚂蚁爬过的路程=3+3
+π≈11.3.
第
24
题:
【答案】
解:(1)∵OF⊥AB,
∴∠BOF=90°,
∵∠B=30°,FO=,
∴OB=6,AB=2OB=12,
又∵AB为⊙
O的直径,
∴∠ACB=90°,
∴AC=AB=6;
(2)∵由(1)可知,AB=12,
∴AO=6,即AC=AO,
在Rt△ACF和Rt△AOF中,
∴Rt△ACF≌Rt△AOF,
∴∠FAO=∠FAC=30°,
∴∠DOB=60°,
过点D作DG⊥AB于点G,
∵OD=6,∴DG=,
∴S△ACF+S△OFD=S△AOD=×6×3=9,
即阴影部分的面积是9.
1
/
12
同课章节目录
