浙教版初中数学八年级上册 1.4 全等三角形 教案
文档属性
| 名称 | 浙教版初中数学八年级上册 1.4 全等三角形 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 14:18:23 | ||
图片预览


文档简介
第一章三角形的初步知识
1.4全等三角形
【教学目标】
1.知识与技能:了解全等图形的概念;会用全等图形的定义判断两个图形是否全等,了解全等三角形的概念,理解全等三角形的性质。
2.过程与方法:借助具体情境,通过观察、实际操作等学习方法,发展学生的识图、推理和有条理地表述问题的能力。
3.情感、态度和价值观:从生活中具体情境抽象出全等图形的概念,从而培养学生用数学的观点考察周围事物的习惯,激发学生学习数学的兴趣。
【重点和难点】1.重点:全等三角形的概念和全等三角形的性质。2.难点:用全等三角形的定义判断两个三角形全等:应用全等三角形的性质进行简单的推理,解决实际问题。
【教学设计】
【创设情景】观察下列图形,你发现了什么?
如果把每一对中的两个图形叠在一起,它们能重合吗?
【探究新知】能够
的两个图形称为
图形。
【练一练】下列各对图形是不是全等图形?为什么?
(1)边长为5cm的两个正方形。
(2)三个角都为30°,60°,90°的两个三角形。
(2)半径相等的两个圆。
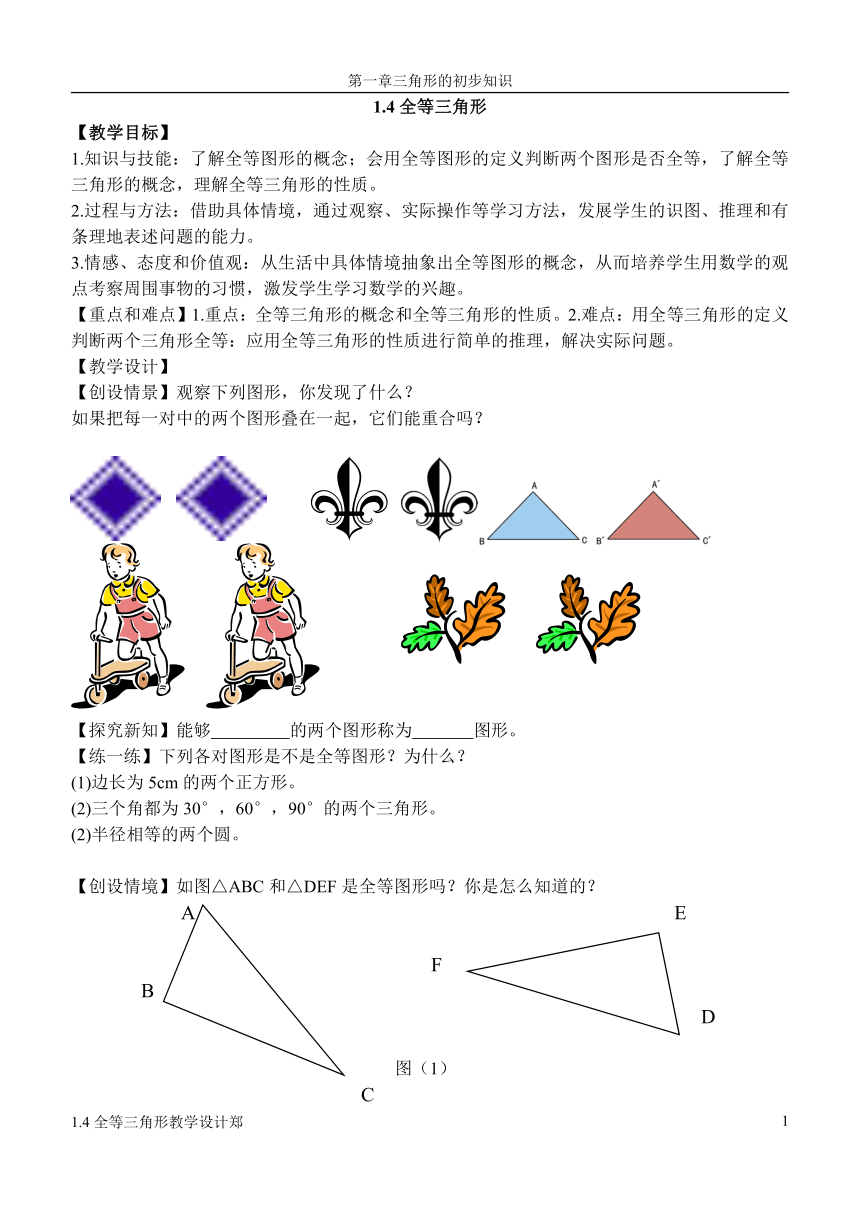
【创设情境】如图△ABC和△DEF是全等图形吗?你是怎么知道的?
A
E
F
B
D
图(1)
C
【探究新知】能够重合的两个三角形叫做
。
两个全等三角形重合时,能互相重合的顶点叫做全等三角形的
,互相重合的边叫做全等三角形的
,互相重合的角叫做全等三角形的
。
如上图,△ABC和△DEF全等,点A和
,
和点E,点C和
分别是对应顶点;AB和
,
和EF,
和DF分别是对应边;∠A和∠D,
和
,
∠C和
分别是对应角。
“全等”可用符号“≌”来表示,如△ABC和△DEF全等,记做“△ABC
△DEF”,读做
“三角形ABC全等于三角形DEF”。
【注】表示两个三角形全等时,通常把对应顶点的字母写在对应位置上。
【练一练】如图2中的两个三角形全等,AB和DC,AC和DB是对应边,
用符号表示这两个三角形全等:△ABC≌△
,
还有一组对应边是
和
,
对应角是∠BAC和
,
∠ABC和
,∠ACB和
。
【动手操作】同桌间相互合作,拿出规格相同的30°三角板,分别指出它们的对应顶点,对应边,对应角,猜猜它们的对应边、对应角有什么数量关系?为什么?
【探究新知】全等三角形的性质:全等三角形的对应边
,对应角
。
几何语言:如图(1):∵△ABC≌△DEF
∴AB=DE,BC=
,
=DF,
∠A=∠D,
=∠E,∠C=
。
【例题精讲】例1如图3,已知△ABC≌△AED,∠B和∠E是一组对应角,请指出其他的对应边和对应角,并指出图中相等的角。
解:对应角:∠BAC与∠
,∠
与∠ADE;
对应边:AB与
,BC与
,
与AD;
相等的角:∠ACB=∠
,∠
=∠E,∠
=∠ECF,
∠BFD=∠
。
例2如图4,AD平分∠BAC,AB=AC。问△ABD与△ACD全等吗?BD和CD相等吗?
∠B与∠C呢?请说明理由。
解:∵AD平分∠BAC
∴∠1=
。
因此将图形沿AD对折时,射线AC和射线
重合。
∵AB=AC,
∴点B与
重合,
也就是△ABD与
重合。
∴△ABD
△ACD
∴BD=CD(
)
∠B=∠C(
)
例3如图5,AB,CD相交于点O,△AOC≌△BOD,A与B是对应顶点。
(1)若∠B=40°,∠BOD=56°,求△AOC各内角的度数;
(2)若AB=3㎝,CD=2㎝,BD=1.5㎝,求△AOC的周长;
解:(1)AB,CD相交于点O,
∴∠AOC=∠
(对顶角相等)
在△BOD中,∠B=40°,∠BOD=56°,
∴∠D=180°-∠B-∠
=180°-40°-
=
(三角形三个内角的和等于180°)
又∵△AOC≌△BOD,A与B是对应顶点(
)
∴∠A=∠
=
,∠C=∠
=
(全等三角形
相等)
(2)∵△AOC≌△BOD,
∴AC=
=1.5(㎝),AO=
=
=
(㎝),CO=
=
=
(㎝)
(全等三角形
相等)
∴△AOC的周长的周长AC+CO+AO=1.5+
+
=
(㎝).
【课堂练习】1、如图6:在△ABC中,AD⊥BC于点D,BD=CD,则∠B=∠C,请完成下面的说理过程。
解:∵AD⊥BC(
)
∴∠ADB=
=Rt∠(
)
当把图形沿AD对折时,射线DB与DC
。
∵BD=CD(
)
∴点B与
重合。
∴△ABD与△ACD
。
∴△ABD
△ACD
∴∠B=∠C(
)。
2、如图7、若把四边形沿对折,点与点重合,写出图中所有全等的三角形和相等的线段。
解:全等的三角形:
相等的线段:
【收获与小结】
能够重合的两个图形称为
。
能够重合的两个三角形叫做
。
全等三角形的性质:全等三角形的对应边
,对应角
。
学生已学过线(直线、射线、线段)、角和相交线与平行线以及三角形的有关知识,这些为学习全等三角形作好了准备。同时,学生积累了一些对图形认识的活动经验,并初步具备了观察、实验、猜想的能力.所以,学生从自然景观、建筑物、艺术作品或日常生活用品中找出形状、大小相同的图形,并通过观察得出形状、大小相同的图形的特征:放在一起能够完全重合,由此得出全等形的概念不会有多大困难.但对“对应”意义的理解,正确区分“对应边”与“对边”、“对应角”与“对角”和在不同位置组合成的两个全等三角形图形中准确地找出对应边、对应角会存在一些困难.因为,学生对“对应”这个词的认识还需有一个过程,需要在后面多次运用中逐步加深理解.“对应边”与“对边”、“对应角”与“对角”容易混淆,学生一时难以区分对应边、对应角是对两个三角形说的,是两条边或两个角之间的关系,而对边、对角是对同一个三角形中边和角的关系说的,对边是对某个角说的,对角是对某个边说的.在现阶段学生的识图能力还处于初级阶段,在较复杂的图形中透视出两个全等三角形的对应元素关系会比较困难.教学中教师应突出图形的教学,通过动手实践感受图形的重合过程,利用多媒体动态演示图形变换(平移、翻折、旋转)过程,让学生充分感受图形重合、图形变换过程中全等三角形的对应元素关系.
PAGE
4
1.4全等三角形教学设计郑
1.4全等三角形
【教学目标】
1.知识与技能:了解全等图形的概念;会用全等图形的定义判断两个图形是否全等,了解全等三角形的概念,理解全等三角形的性质。
2.过程与方法:借助具体情境,通过观察、实际操作等学习方法,发展学生的识图、推理和有条理地表述问题的能力。
3.情感、态度和价值观:从生活中具体情境抽象出全等图形的概念,从而培养学生用数学的观点考察周围事物的习惯,激发学生学习数学的兴趣。
【重点和难点】1.重点:全等三角形的概念和全等三角形的性质。2.难点:用全等三角形的定义判断两个三角形全等:应用全等三角形的性质进行简单的推理,解决实际问题。
【教学设计】
【创设情景】观察下列图形,你发现了什么?
如果把每一对中的两个图形叠在一起,它们能重合吗?
【探究新知】能够
的两个图形称为
图形。
【练一练】下列各对图形是不是全等图形?为什么?
(1)边长为5cm的两个正方形。
(2)三个角都为30°,60°,90°的两个三角形。
(2)半径相等的两个圆。
【创设情境】如图△ABC和△DEF是全等图形吗?你是怎么知道的?
A
E
F
B
D
图(1)
C
【探究新知】能够重合的两个三角形叫做
。
两个全等三角形重合时,能互相重合的顶点叫做全等三角形的
,互相重合的边叫做全等三角形的
,互相重合的角叫做全等三角形的
。
如上图,△ABC和△DEF全等,点A和
,
和点E,点C和
分别是对应顶点;AB和
,
和EF,
和DF分别是对应边;∠A和∠D,
和
,
∠C和
分别是对应角。
“全等”可用符号“≌”来表示,如△ABC和△DEF全等,记做“△ABC
△DEF”,读做
“三角形ABC全等于三角形DEF”。
【注】表示两个三角形全等时,通常把对应顶点的字母写在对应位置上。
【练一练】如图2中的两个三角形全等,AB和DC,AC和DB是对应边,
用符号表示这两个三角形全等:△ABC≌△
,
还有一组对应边是
和
,
对应角是∠BAC和
,
∠ABC和
,∠ACB和
。
【动手操作】同桌间相互合作,拿出规格相同的30°三角板,分别指出它们的对应顶点,对应边,对应角,猜猜它们的对应边、对应角有什么数量关系?为什么?
【探究新知】全等三角形的性质:全等三角形的对应边
,对应角
。
几何语言:如图(1):∵△ABC≌△DEF
∴AB=DE,BC=
,
=DF,
∠A=∠D,
=∠E,∠C=
。
【例题精讲】例1如图3,已知△ABC≌△AED,∠B和∠E是一组对应角,请指出其他的对应边和对应角,并指出图中相等的角。
解:对应角:∠BAC与∠
,∠
与∠ADE;
对应边:AB与
,BC与
,
与AD;
相等的角:∠ACB=∠
,∠
=∠E,∠
=∠ECF,
∠BFD=∠
。
例2如图4,AD平分∠BAC,AB=AC。问△ABD与△ACD全等吗?BD和CD相等吗?
∠B与∠C呢?请说明理由。
解:∵AD平分∠BAC
∴∠1=
。
因此将图形沿AD对折时,射线AC和射线
重合。
∵AB=AC,
∴点B与
重合,
也就是△ABD与
重合。
∴△ABD
△ACD
∴BD=CD(
)
∠B=∠C(
)
例3如图5,AB,CD相交于点O,△AOC≌△BOD,A与B是对应顶点。
(1)若∠B=40°,∠BOD=56°,求△AOC各内角的度数;
(2)若AB=3㎝,CD=2㎝,BD=1.5㎝,求△AOC的周长;
解:(1)AB,CD相交于点O,
∴∠AOC=∠
(对顶角相等)
在△BOD中,∠B=40°,∠BOD=56°,
∴∠D=180°-∠B-∠
=180°-40°-
=
(三角形三个内角的和等于180°)
又∵△AOC≌△BOD,A与B是对应顶点(
)
∴∠A=∠
=
,∠C=∠
=
(全等三角形
相等)
(2)∵△AOC≌△BOD,
∴AC=
=1.5(㎝),AO=
=
=
(㎝),CO=
=
=
(㎝)
(全等三角形
相等)
∴△AOC的周长的周长AC+CO+AO=1.5+
+
=
(㎝).
【课堂练习】1、如图6:在△ABC中,AD⊥BC于点D,BD=CD,则∠B=∠C,请完成下面的说理过程。
解:∵AD⊥BC(
)
∴∠ADB=
=Rt∠(
)
当把图形沿AD对折时,射线DB与DC
。
∵BD=CD(
)
∴点B与
重合。
∴△ABD与△ACD
。
∴△ABD
△ACD
∴∠B=∠C(
)。
2、如图7、若把四边形沿对折,点与点重合,写出图中所有全等的三角形和相等的线段。
解:全等的三角形:
相等的线段:
【收获与小结】
能够重合的两个图形称为
。
能够重合的两个三角形叫做
。
全等三角形的性质:全等三角形的对应边
,对应角
。
学生已学过线(直线、射线、线段)、角和相交线与平行线以及三角形的有关知识,这些为学习全等三角形作好了准备。同时,学生积累了一些对图形认识的活动经验,并初步具备了观察、实验、猜想的能力.所以,学生从自然景观、建筑物、艺术作品或日常生活用品中找出形状、大小相同的图形,并通过观察得出形状、大小相同的图形的特征:放在一起能够完全重合,由此得出全等形的概念不会有多大困难.但对“对应”意义的理解,正确区分“对应边”与“对边”、“对应角”与“对角”和在不同位置组合成的两个全等三角形图形中准确地找出对应边、对应角会存在一些困难.因为,学生对“对应”这个词的认识还需有一个过程,需要在后面多次运用中逐步加深理解.“对应边”与“对边”、“对应角”与“对角”容易混淆,学生一时难以区分对应边、对应角是对两个三角形说的,是两条边或两个角之间的关系,而对边、对角是对同一个三角形中边和角的关系说的,对边是对某个角说的,对角是对某个边说的.在现阶段学生的识图能力还处于初级阶段,在较复杂的图形中透视出两个全等三角形的对应元素关系会比较困难.教学中教师应突出图形的教学,通过动手实践感受图形的重合过程,利用多媒体动态演示图形变换(平移、翻折、旋转)过程,让学生充分感受图形重合、图形变换过程中全等三角形的对应元素关系.
PAGE
4
1.4全等三角形教学设计郑
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
