浙教版初中数学八年级上册4.2 平面直角坐标系 教案
文档属性
| 名称 | 浙教版初中数学八年级上册4.2 平面直角坐标系 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 478.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 00:00:00 | ||
图片预览


文档简介
平面直角坐标系
教学目标:
1.在具体情景中理解有序实数对的意义,经历从现实生活中抽象出数学概念的过程,感受数学与生活的联系.
2.理解平面直角坐标系的有关概念,知道坐标平面内的点与有序实数对是一一对应的意义.
3.会根据直角坐标系内点的位置写出它的坐标,体会数形结合的数学思想.
教学重点:
平面直角坐标系的有关概念,直角坐标内点坐标的确定.
教学难点:
平面直角坐标系中的点与有序实数对对应的意义.
教学过程:
教师活动
学生活动
设计意图
一、复习旧知
问:我们说,数轴上的所有点与实数的具有对应关系,你是如何理解这句话的?这种对应关系我们称为:一一对应.二、情景引入问1:可以用什么方法来表示你在教室中坐的位置?
问2:在电影院看电影时,用什么方法表示你的座位?
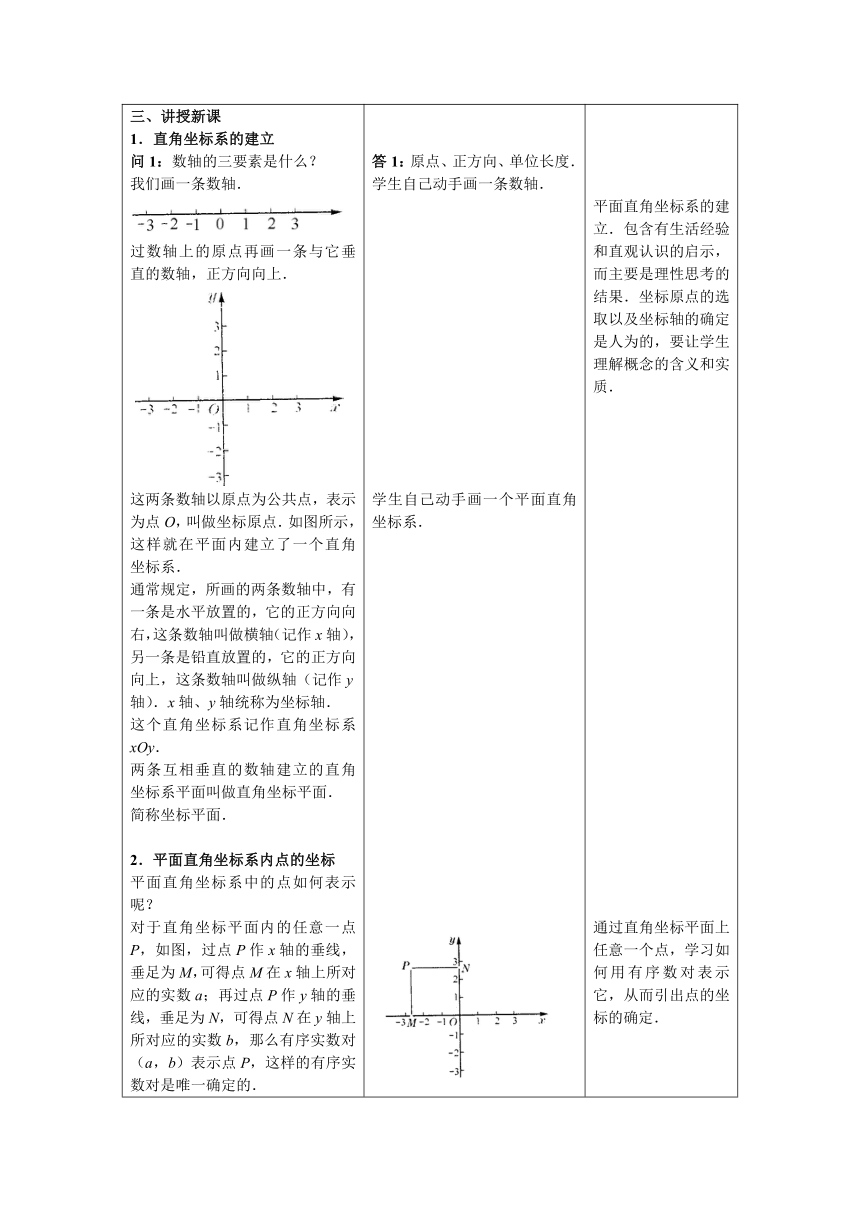
在上面两个问题中,我们用“数对”来表示平面内的点.在数学中,我们也用“数对”来表示平面内点的位置.思考:如何确定平面内的点的位置?(例如图A、B、C、D、E各点)你能用数对来表示上述各点的位置吗?三、讲授新课1.直角坐标系的建立问1:数轴的三要素是什么?我们画一条数轴.过数轴上的原点再画一条与它垂直的数轴,正方向向上.这两条数轴以原点为公共点,表示为点O,叫做坐标原点.如图所示,这样就在平面内建立了一个直角坐标系.通常规定,所画的两条数轴中,有一条是水平放置的,它的正方向向右,这条数轴叫做横轴(记作x轴),另一条是铅直放置的,它的正方向向上,这条数轴叫做纵轴(记作y轴).x轴、y轴统称为坐标轴.这个直角坐标系记作直角坐标系xOy.两条互相垂直的数轴建立的直角坐标系平面叫做直角坐标平面.简称坐标平面.2.平面直角坐标系内点的坐标平面直角坐标系中的点如何表示呢?对于直角坐标平面内的任意一点P,如图,过点P作x轴的垂线,垂足为M,可得点M在x轴上所对应的实数a;再过点P作y轴的垂线,垂足为N,可得点N在y轴上所对应的实数b,那么有序实数对(a,b)表示点P,这样的有序实数对是唯一确定的.在直角坐标系xoy中,点P所对应的有序实数对(a,b)叫做点P的坐标,记作P(a,b),其中a叫做横坐标,b叫做纵坐标.问3:有序数对(2,4)和(4,2)在直角坐标平面内表示的是不是同一点?【适时小结】在(a,b)中,a、b顺序不能颠倒.当a≠b时,(a,b)与(b,a)表示不同的点.当a=b时,(a,b)与(b,a)表示相同的点.四、简单应用例题1
写出图中直角坐标平面内各点的坐标.问:如何找到点A的坐标?解:过点A作x轴的垂线,垂足在x轴上对应的实数是3;再过点A作y轴的垂线,垂足在y轴上对应的实数是4,所以点A的坐标是(3,4);点B的坐标是(–3,1);点C的坐标是(–2,–3);点D的坐标是(5,–2).例题2
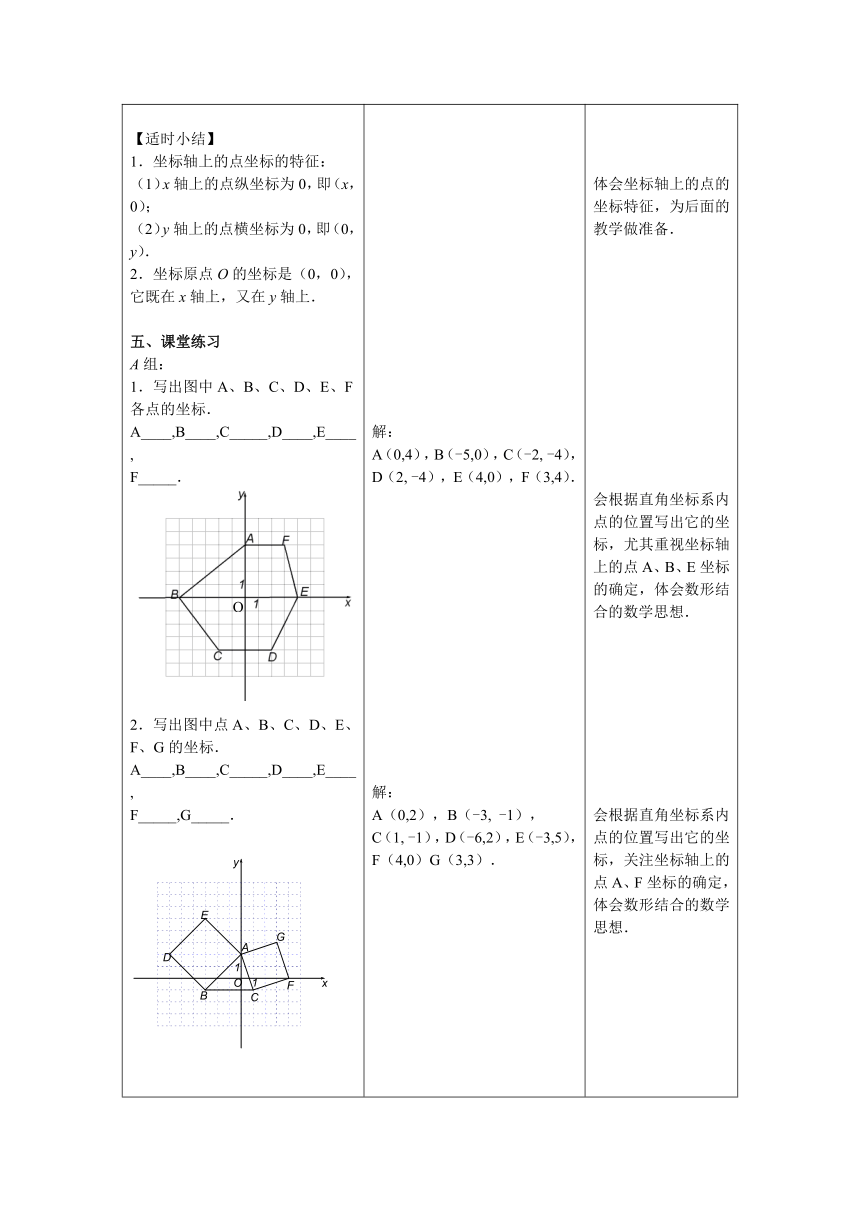
写出图中坐标轴上的点E、F的坐标.解:过点E作x轴的垂线,垂足为E,点E在x轴上对应的实数是–4;再过点E作y轴的垂线,垂足为O,点O在y轴上对应的实数是0,因此点E的横坐标是–4,纵坐标是0,所以点E的坐标是(–4,0).点F的坐标是(0,2).问:点O的坐标是什么?【适时小结】1.坐标轴上的点坐标的特征:(1)x轴上的点纵坐标为0,即(x,0);(2)y轴上的点横坐标为0,即(0,y).2.坐标原点O的坐标是(0,0),它既在x轴上,又在y轴上.五、课堂练习A组:1.写出图中A、B、C、D、E、F各点的坐标.
A____,B____,C_____,D____,E____,F_____.2.写出图中点A、B、C、D、E、F、G的坐标.
A____,B____,C_____,D____,E____,F_____,G_____.B组:在直角坐标平面内,横坐标与纵坐标都是整数的点叫做格点;顶点都是格点的三角形叫做格点三角形.如图,已知格点A(-2,1),请画一个格点三角形,使A在它内部且这个三角形的面积最小,并写出这个三角形各个顶点的坐标.六、课堂小结1.平面直角坐标系的有关知识.2.体会数学思想.
答:每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点也都可以用唯一的一个实数来表示.答1:用第几行第几列表示.答2:用第几排第几座表示.答3:也用
“数对”来表示.预设学生回答:能.从左数或从右数,从上数或从下数,回答第几列,第几行,这就用数对表示了平面内这些点的位置.答1:原点、正方向、单位长度.学生自己动手画一条数轴.学生自己动手画一个平面直角坐标系.答3:不是同一个点.学生用老师讲解的方法,分别写出点B、点C、点D的坐标.
学生用类似的方法,写出点F的坐标.答:点O的坐标是(0,0).解:A(0,4),B(-5,0),C(-2,
-4),D(2,
-4),E(4,0),F(3,4).解:A(0,2),B(-3,
-1),C(1,
-1),D(-6,2),E(-3,5),F(4,0)G(3,3).解:有4种情况①(-3,0),(-2,2),(-1,1);②(-2,0),(-3,2),(-1,1);③(-1,0),(-3,1),(-2,2);④(-2,0),(-3,1),(-1,2).师生共同总结:1.平面直角坐标系.2.平面直角坐标系中的横轴(x轴),纵轴(y轴),坐标原点O.3.点的坐标表示方法:P(a,b).数形结合思想.
复习旧知,为本节课做好知识储备.创设问题情境,导入新课.通过生活实际问题抽象出用一对实数来表示平面上点的位置的数学问题.由此可以考虑,用“数对”来表示平面内的点.平面直角坐标系的建立.包含有生活经验和直观认识的启示,而主要是理性思考的结果.坐标原点的选取以及坐标轴的确定是人为的,要让学生理解概念的含义和实质.
通过直角坐标平面上任意一个点,学习如何用有序数对表示它,从而引出点的坐标的确定.强调数对的有序性.通过例题1,学会根据直角坐标系内点的位置写出它的坐标,体会数形结合的数学思想.通过例题2让学生发现:凡是x轴上的点作y轴的垂线,垂足在y轴上对应的实数总是0,凡是y轴上的点作x轴的垂线,垂足在x轴上对应的实数总是0.体会坐标轴上的点的坐标特征,为后面的教学做准备.会根据直角坐标系内点的位置写出它的坐标,尤其重视坐标轴上的点A、B、E坐标的确定,体会数形结合的数学思想.会根据直角坐标系内点的位置写出它的坐标,关注坐标轴上的点A、F坐标的确定,体会数形结合的数学思想.会根据直角坐标系内点的位置写出它的坐标,尤其重视坐标轴上的点A、B、E坐标的确定,体会数形结合的数学思想.总结问题解决过程中的经验教训,理顺思路,从而进一步完善学生的认知结构.
课后作业
试
题
解
答
设计意图
A组:1.写出直角坐标平面内“一帆风顺”图形中下列各点的坐标.A____,B____,O_____,C_____,D____,E____,
F_____.
解:A(0,8),B(4,2),C(-5,
0),D(-4,
-2),E(4,-2),F(5,0).
会根据直角坐标系内点的位置写出它的坐标,感受成轴对称的点D与点E,点C与点F的坐标关系,体会数形结合的数学思想.
2.写出图中下列各点的坐标.A____,B____,C_____,D____,E____,
F____,G_____,H____.
解:A(-1,4),B(-4,
-1),C(1,
-4),D(4,
1),E(-1,1),F(-1,-1),G(1,-1),H(1,1).
会根据直角坐标系内点的位置写出它的坐标,感受以坐标原点为对称中心的中心对称图形中的点的坐标关系,认识其中的全等三角形.
3.
写出直角坐标平面内信封图形中下列各点的坐标:A____,B____,C_____,D____,E____,
F____.
解:A(-4,4),B(-4,
-2),C(4,
-2
),D(4,
4),E(-1,1),F(1,1).
会根据直角坐标系内点的位置写出它的坐标,体会轴对称图形中,对应点的坐标之间的关系.
4.如图:(1)写出图中A、B、C的坐标.(2)△ABC是否为等腰三角形?为什么?(提示:利用三角形全等)
解:(1)A(6,6),B(0,
3),C(3,
0
).(2)答:△ABC是等腰三角形.解:过点A作AE⊥y轴,AF⊥y轴垂足分别为E、F根据题意,得AE=6,AF=6,CF=3,BE=3,∠AEB=∠AFC=90°在△AEB和△AFC中
∴△AEB≌△AFC(S.A.S)
会根据直角坐标系内点的位置写出它的坐标.学会构造全等三角形说明线段相等,并初步学会把点的坐标转化为线段的长度判定三角形全等.
B组:
1.在轴上,求与原点的距离为3的点的坐标.
分析:在轴上,求与原点的距离为3的点有两个,一个在原点的左侧,一个在原点的右侧,而且在轴上的点的纵坐标为0.解:(-3,0)或(3,0).
理解轴上的点坐标特征.
2.已知点P(m+1,2-m)在轴上,求点P的坐标.
分析:轴上的点坐标特征是横坐标为0.解:∵点P(m+1,2-m)在轴上∴m+1=0,∴m=-1,∴点P的坐标为(0,3).
3.在直角坐标平面内,O为坐标原点,点P坐标为(3,0),将OP绕原点逆时针旋转90°后的线段为OQ,求点Q的坐标.
分析:先画出符合题意的图形再确定点Q的坐标.解:点Q的坐标为(0,3).
渗透图形运动思想,分清旋转方向、旋转中心.体会线段的长与点的坐标之间的关系.
O
PAGE
教学目标:
1.在具体情景中理解有序实数对的意义,经历从现实生活中抽象出数学概念的过程,感受数学与生活的联系.
2.理解平面直角坐标系的有关概念,知道坐标平面内的点与有序实数对是一一对应的意义.
3.会根据直角坐标系内点的位置写出它的坐标,体会数形结合的数学思想.
教学重点:
平面直角坐标系的有关概念,直角坐标内点坐标的确定.
教学难点:
平面直角坐标系中的点与有序实数对对应的意义.
教学过程:
教师活动
学生活动
设计意图
一、复习旧知
问:我们说,数轴上的所有点与实数的具有对应关系,你是如何理解这句话的?这种对应关系我们称为:一一对应.二、情景引入问1:可以用什么方法来表示你在教室中坐的位置?
问2:在电影院看电影时,用什么方法表示你的座位?
在上面两个问题中,我们用“数对”来表示平面内的点.在数学中,我们也用“数对”来表示平面内点的位置.思考:如何确定平面内的点的位置?(例如图A、B、C、D、E各点)你能用数对来表示上述各点的位置吗?三、讲授新课1.直角坐标系的建立问1:数轴的三要素是什么?我们画一条数轴.过数轴上的原点再画一条与它垂直的数轴,正方向向上.这两条数轴以原点为公共点,表示为点O,叫做坐标原点.如图所示,这样就在平面内建立了一个直角坐标系.通常规定,所画的两条数轴中,有一条是水平放置的,它的正方向向右,这条数轴叫做横轴(记作x轴),另一条是铅直放置的,它的正方向向上,这条数轴叫做纵轴(记作y轴).x轴、y轴统称为坐标轴.这个直角坐标系记作直角坐标系xOy.两条互相垂直的数轴建立的直角坐标系平面叫做直角坐标平面.简称坐标平面.2.平面直角坐标系内点的坐标平面直角坐标系中的点如何表示呢?对于直角坐标平面内的任意一点P,如图,过点P作x轴的垂线,垂足为M,可得点M在x轴上所对应的实数a;再过点P作y轴的垂线,垂足为N,可得点N在y轴上所对应的实数b,那么有序实数对(a,b)表示点P,这样的有序实数对是唯一确定的.在直角坐标系xoy中,点P所对应的有序实数对(a,b)叫做点P的坐标,记作P(a,b),其中a叫做横坐标,b叫做纵坐标.问3:有序数对(2,4)和(4,2)在直角坐标平面内表示的是不是同一点?【适时小结】在(a,b)中,a、b顺序不能颠倒.当a≠b时,(a,b)与(b,a)表示不同的点.当a=b时,(a,b)与(b,a)表示相同的点.四、简单应用例题1
写出图中直角坐标平面内各点的坐标.问:如何找到点A的坐标?解:过点A作x轴的垂线,垂足在x轴上对应的实数是3;再过点A作y轴的垂线,垂足在y轴上对应的实数是4,所以点A的坐标是(3,4);点B的坐标是(–3,1);点C的坐标是(–2,–3);点D的坐标是(5,–2).例题2
写出图中坐标轴上的点E、F的坐标.解:过点E作x轴的垂线,垂足为E,点E在x轴上对应的实数是–4;再过点E作y轴的垂线,垂足为O,点O在y轴上对应的实数是0,因此点E的横坐标是–4,纵坐标是0,所以点E的坐标是(–4,0).点F的坐标是(0,2).问:点O的坐标是什么?【适时小结】1.坐标轴上的点坐标的特征:(1)x轴上的点纵坐标为0,即(x,0);(2)y轴上的点横坐标为0,即(0,y).2.坐标原点O的坐标是(0,0),它既在x轴上,又在y轴上.五、课堂练习A组:1.写出图中A、B、C、D、E、F各点的坐标.
A____,B____,C_____,D____,E____,F_____.2.写出图中点A、B、C、D、E、F、G的坐标.
A____,B____,C_____,D____,E____,F_____,G_____.B组:在直角坐标平面内,横坐标与纵坐标都是整数的点叫做格点;顶点都是格点的三角形叫做格点三角形.如图,已知格点A(-2,1),请画一个格点三角形,使A在它内部且这个三角形的面积最小,并写出这个三角形各个顶点的坐标.六、课堂小结1.平面直角坐标系的有关知识.2.体会数学思想.
答:每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点也都可以用唯一的一个实数来表示.答1:用第几行第几列表示.答2:用第几排第几座表示.答3:也用
“数对”来表示.预设学生回答:能.从左数或从右数,从上数或从下数,回答第几列,第几行,这就用数对表示了平面内这些点的位置.答1:原点、正方向、单位长度.学生自己动手画一条数轴.学生自己动手画一个平面直角坐标系.答3:不是同一个点.学生用老师讲解的方法,分别写出点B、点C、点D的坐标.
学生用类似的方法,写出点F的坐标.答:点O的坐标是(0,0).解:A(0,4),B(-5,0),C(-2,
-4),D(2,
-4),E(4,0),F(3,4).解:A(0,2),B(-3,
-1),C(1,
-1),D(-6,2),E(-3,5),F(4,0)G(3,3).解:有4种情况①(-3,0),(-2,2),(-1,1);②(-2,0),(-3,2),(-1,1);③(-1,0),(-3,1),(-2,2);④(-2,0),(-3,1),(-1,2).师生共同总结:1.平面直角坐标系.2.平面直角坐标系中的横轴(x轴),纵轴(y轴),坐标原点O.3.点的坐标表示方法:P(a,b).数形结合思想.
复习旧知,为本节课做好知识储备.创设问题情境,导入新课.通过生活实际问题抽象出用一对实数来表示平面上点的位置的数学问题.由此可以考虑,用“数对”来表示平面内的点.平面直角坐标系的建立.包含有生活经验和直观认识的启示,而主要是理性思考的结果.坐标原点的选取以及坐标轴的确定是人为的,要让学生理解概念的含义和实质.
通过直角坐标平面上任意一个点,学习如何用有序数对表示它,从而引出点的坐标的确定.强调数对的有序性.通过例题1,学会根据直角坐标系内点的位置写出它的坐标,体会数形结合的数学思想.通过例题2让学生发现:凡是x轴上的点作y轴的垂线,垂足在y轴上对应的实数总是0,凡是y轴上的点作x轴的垂线,垂足在x轴上对应的实数总是0.体会坐标轴上的点的坐标特征,为后面的教学做准备.会根据直角坐标系内点的位置写出它的坐标,尤其重视坐标轴上的点A、B、E坐标的确定,体会数形结合的数学思想.会根据直角坐标系内点的位置写出它的坐标,关注坐标轴上的点A、F坐标的确定,体会数形结合的数学思想.会根据直角坐标系内点的位置写出它的坐标,尤其重视坐标轴上的点A、B、E坐标的确定,体会数形结合的数学思想.总结问题解决过程中的经验教训,理顺思路,从而进一步完善学生的认知结构.
课后作业
试
题
解
答
设计意图
A组:1.写出直角坐标平面内“一帆风顺”图形中下列各点的坐标.A____,B____,O_____,C_____,D____,E____,
F_____.
解:A(0,8),B(4,2),C(-5,
0),D(-4,
-2),E(4,-2),F(5,0).
会根据直角坐标系内点的位置写出它的坐标,感受成轴对称的点D与点E,点C与点F的坐标关系,体会数形结合的数学思想.
2.写出图中下列各点的坐标.A____,B____,C_____,D____,E____,
F____,G_____,H____.
解:A(-1,4),B(-4,
-1),C(1,
-4),D(4,
1),E(-1,1),F(-1,-1),G(1,-1),H(1,1).
会根据直角坐标系内点的位置写出它的坐标,感受以坐标原点为对称中心的中心对称图形中的点的坐标关系,认识其中的全等三角形.
3.
写出直角坐标平面内信封图形中下列各点的坐标:A____,B____,C_____,D____,E____,
F____.
解:A(-4,4),B(-4,
-2),C(4,
-2
),D(4,
4),E(-1,1),F(1,1).
会根据直角坐标系内点的位置写出它的坐标,体会轴对称图形中,对应点的坐标之间的关系.
4.如图:(1)写出图中A、B、C的坐标.(2)△ABC是否为等腰三角形?为什么?(提示:利用三角形全等)
解:(1)A(6,6),B(0,
3),C(3,
0
).(2)答:△ABC是等腰三角形.解:过点A作AE⊥y轴,AF⊥y轴垂足分别为E、F根据题意,得AE=6,AF=6,CF=3,BE=3,∠AEB=∠AFC=90°在△AEB和△AFC中
∴△AEB≌△AFC(S.A.S)
会根据直角坐标系内点的位置写出它的坐标.学会构造全等三角形说明线段相等,并初步学会把点的坐标转化为线段的长度判定三角形全等.
B组:
1.在轴上,求与原点的距离为3的点的坐标.
分析:在轴上,求与原点的距离为3的点有两个,一个在原点的左侧,一个在原点的右侧,而且在轴上的点的纵坐标为0.解:(-3,0)或(3,0).
理解轴上的点坐标特征.
2.已知点P(m+1,2-m)在轴上,求点P的坐标.
分析:轴上的点坐标特征是横坐标为0.解:∵点P(m+1,2-m)在轴上∴m+1=0,∴m=-1,∴点P的坐标为(0,3).
3.在直角坐标平面内,O为坐标原点,点P坐标为(3,0),将OP绕原点逆时针旋转90°后的线段为OQ,求点Q的坐标.
分析:先画出符合题意的图形再确定点Q的坐标.解:点Q的坐标为(0,3).
渗透图形运动思想,分清旋转方向、旋转中心.体会线段的长与点的坐标之间的关系.
O
PAGE
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
