相似三角形分类讨论
图片预览

文档简介
(共33张PPT)
A
E
D
B
C
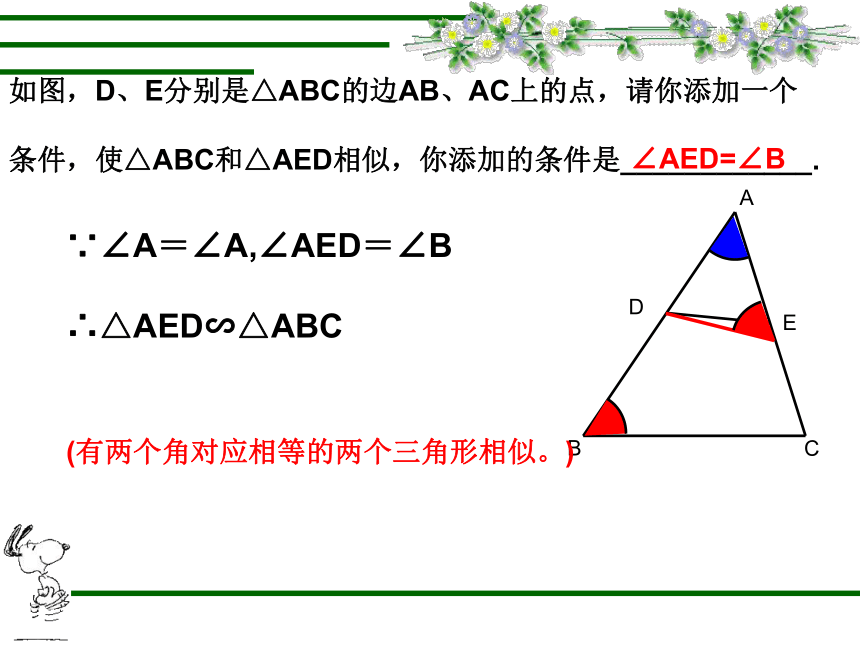
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠AED=∠B
∵∠A=∠A,∠AED=∠B
∴△AED∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
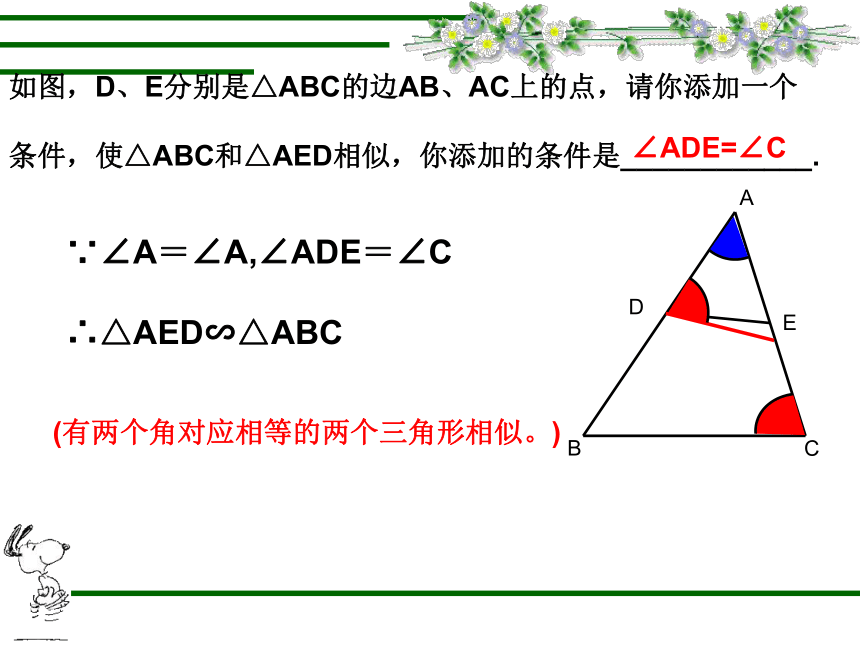
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠ADE=∠C
∵∠A=∠A,∠ADE=∠C
∴△AED∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
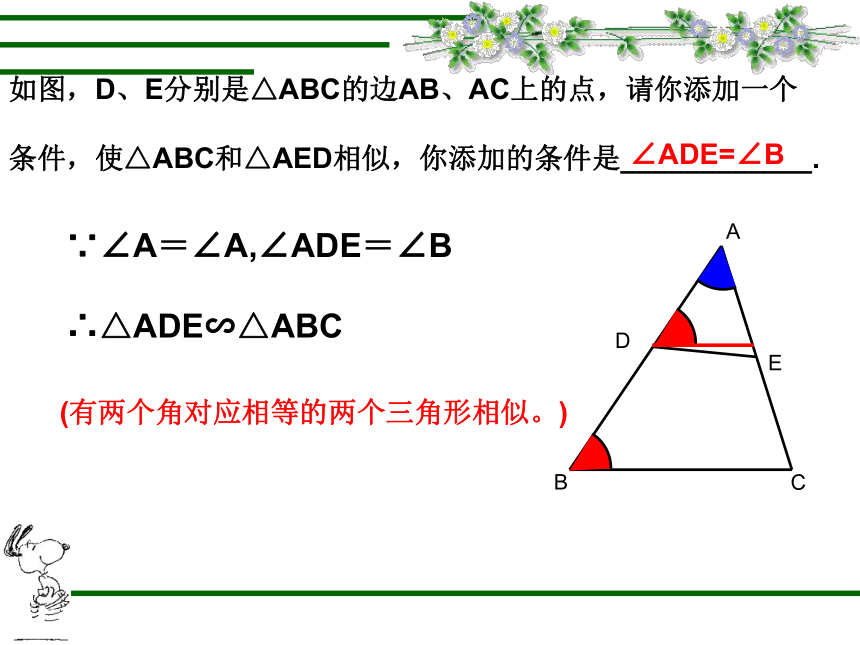
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠ADE=∠B
∵∠A=∠A,∠ADE=∠B
∴△ADE∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
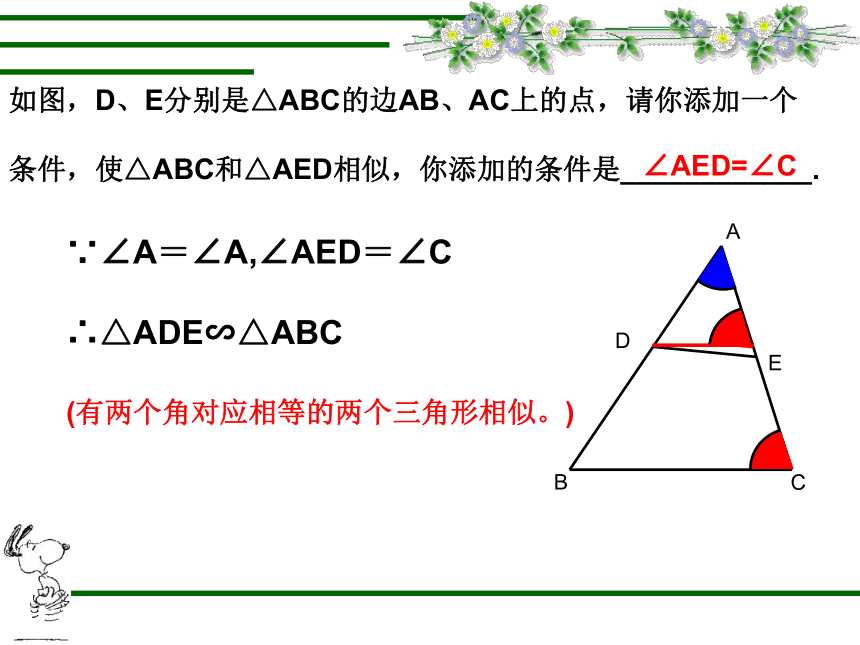
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠AED=∠C
∵∠A=∠A,∠AED=∠C
∴△ADE∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
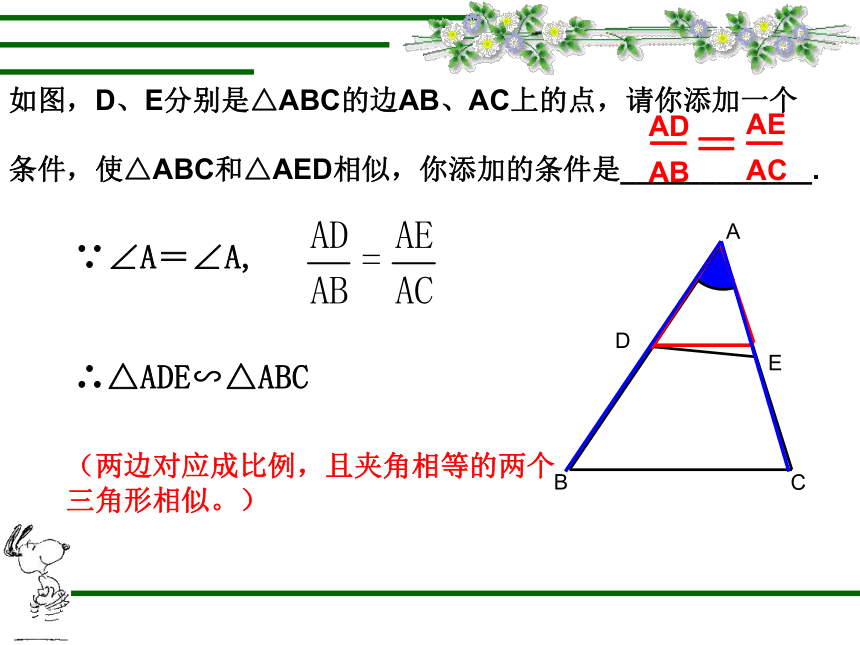
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
AD
AB
-=-
AE
AC
∵∠A=∠A,
∴△ADE∽△ABC
(两边对应成比例,且夹角相等的两个
三角形相似。)
A
E
D
B
C
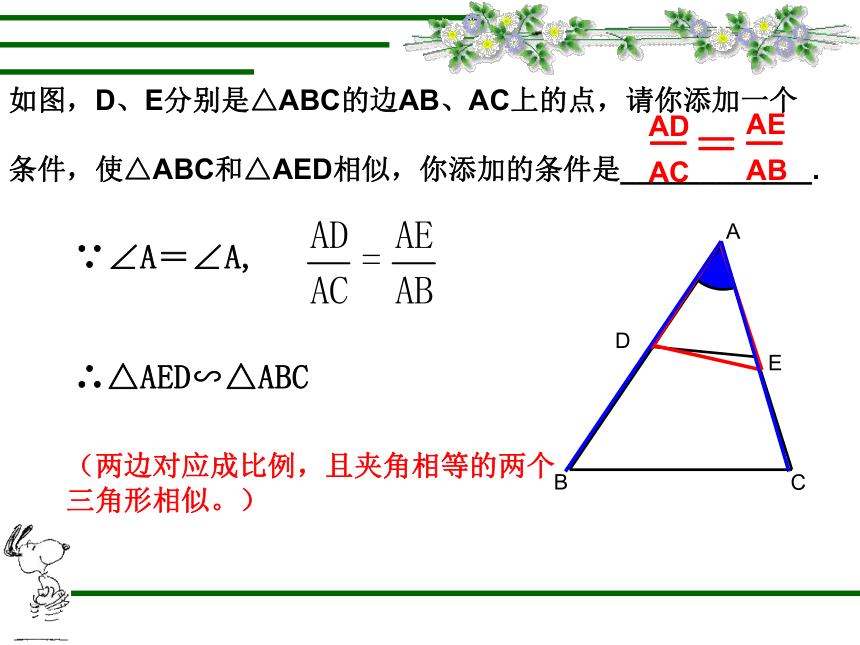
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
AD
AC
-=-
AE
AB
∵∠A=∠A,
∴△AED∽△ABC
(两边对应成比例,且夹角相等的两个
三角形相似。)
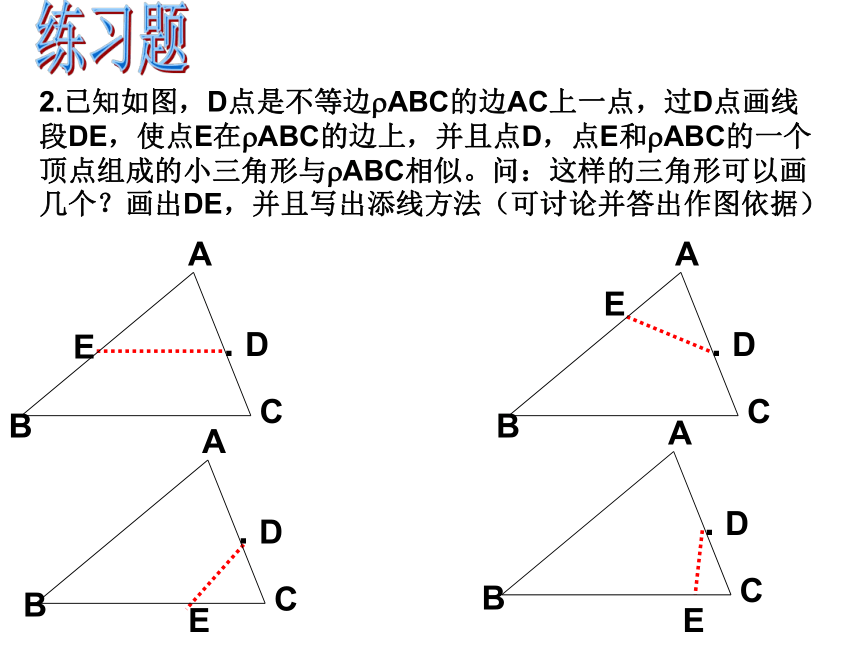
2.已知如图,D点是不等边 ABC的边AC上一点,过D点画线段DE,使点E在 ABC的边上,并且点D,点E和 ABC的一个顶点组成的小三角形与 ABC相似。问:这样的三角形可以画几个?画出DE,并且写出添线方法(可讨论并答出作图依据)
A
C
. D
B
A
C
. D
B
B
A
C
. D
A
C
. D
B
E
E
E
E
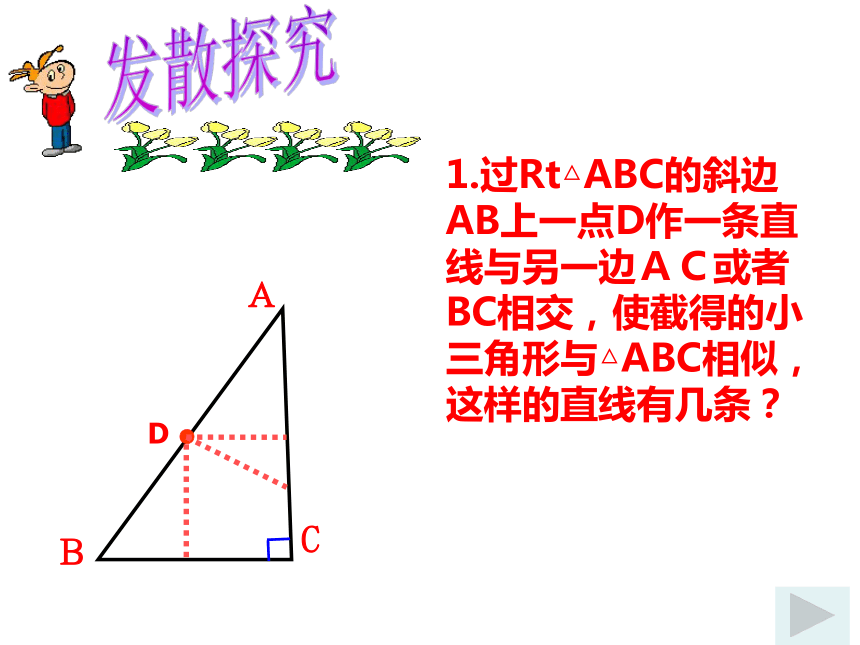
1.过Rt△ABC的斜边AB上一点D作一条直线与另一边AC或者BC相交,使截得的小三角形与△ABC相似,这样的直线有几条?
A
C
D ●
A
B
E
A
B
C
.
1、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________
F2
F1
练一练
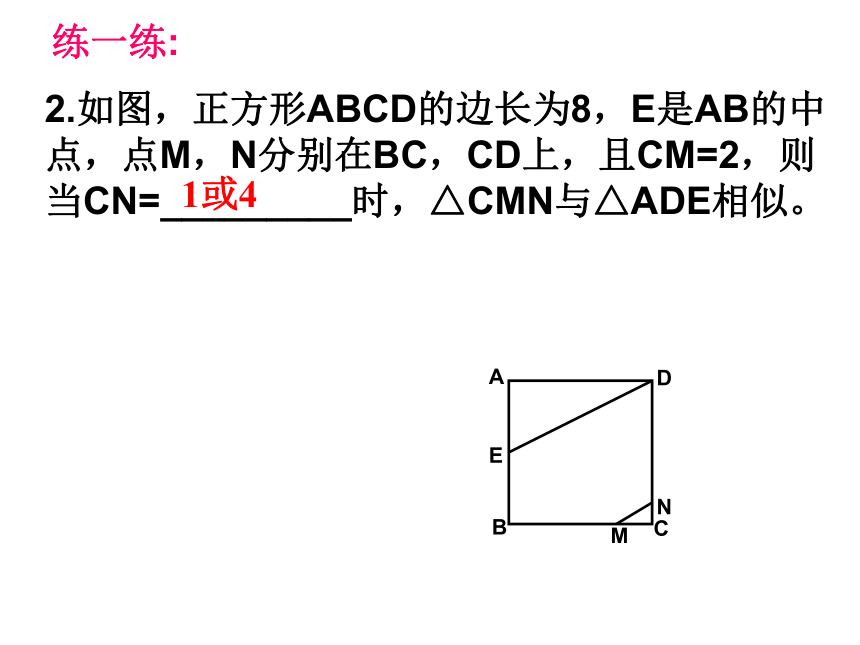
2.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE相似。
E
A
B
C
D
M
N
1或4
练一练:
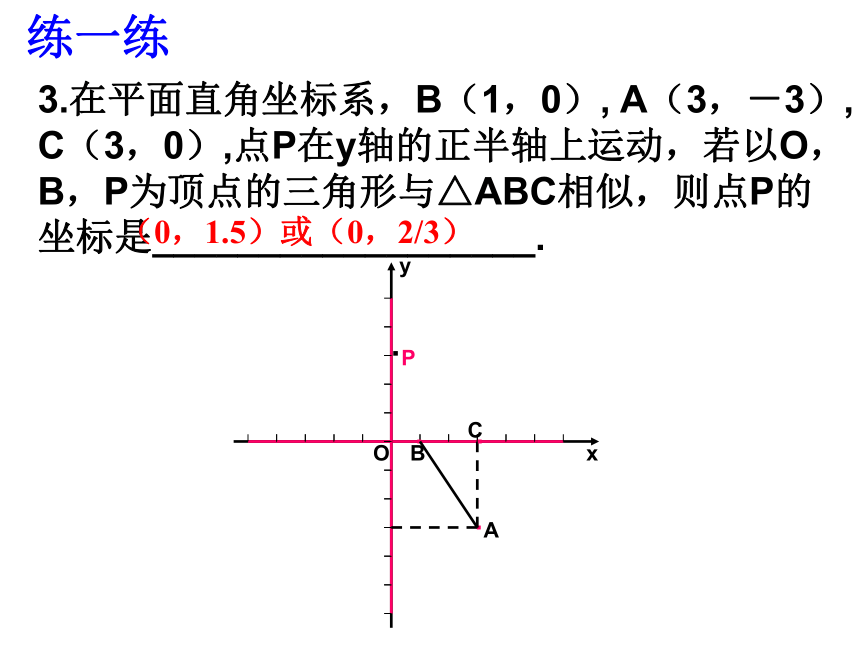
3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
(0,1.5)或(0,2/3)
练一练
C
A
O
B
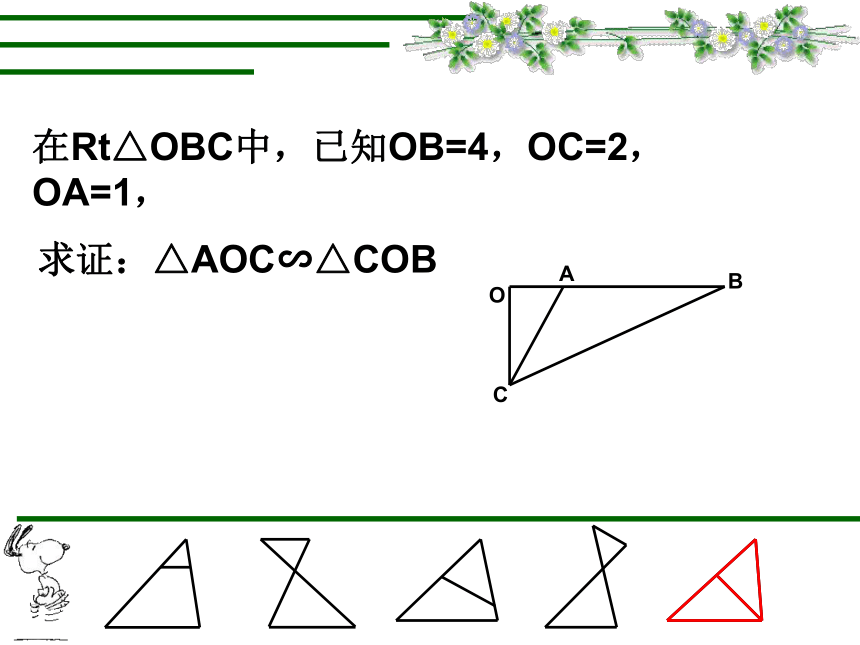
在Rt△OBC中,已知OB=4,OC=2,OA=1,
求证:△AOC∽△COB
C
A
O
在直线AC上是否存在点M,
使得以A,B,M为顶点的三
角形和△AOC相似,若不存
在,请说明理由.若存在,这样
的M点共有几个 请求出AM
的长。
M
M
OB=4,OC=2,OA=1
B
在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.
x
y
4
-1
-1
4
3
2
1
3
0
1
2
A
-4
-3
-2
-4
-3
-2
B
5
-5
作一个格点三角形与△OAB相似且与△OAB 共边AB.
●
●
●
●
●
4. 如图,平面直角坐标系中,直线AB与x轴y轴分别A(3,0)B(0, )两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
(1)求直线AB的解析式;
(2)在第一象限内求作一点P,使得以P,O,B为顶点的三角形与⊿OBA相似,并求出所有符合条件的点P.
A
O
D
C
B
y
x
C
A
O
B
x
y
OB=4,OC=2,OA=1
D
过点C作 CD∥x轴,一动点P从
点A出发,以每秒1个单位长度
的速度匀速向B点运动,同时动
点Q从C点出发沿射线CD以每
秒2个单位长度的速度匀速运动,
当P达到B后,运动停止,设运动时间为t.连结PQ交CB于点E。
P
E
(1)经过几秒后,S△CEQ=4S△BPE
(2)在运动过程中,当BE:EC=1:4时,请写出E点的坐标.
Q
你能判断PQ与BC的位置关系吗
1、如图, 已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP. 试问在射线BF上是否存在一点E,使以点B、E、C为顶点的三角形与△ABP相似 若存在,请求出BE的长;若不存在,请说明理由.
F
C
A
B
D
P
E
E
相应练习
B
C
A
Q
P
8
16
2cm/秒
4cm/秒
练一练
2、在 ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟 BPQ与 BAC相似?
练一练
3、如图:已知∠ABC=∠CDB=90°,AC=5cm,BC=3cm,当BD取多少cm时 △ABC和△BDC相似?
4
D
A
B
C
5
3
4.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QPBC的面积,提出一个与计算结果有关的结论;
(3)那么当t为何值时,以点Q、A、P为顶点的三角形和△ABC相似
2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似
D
A
B
C
a
b
解:⑴∵ ∠1=∠D=90°
∴当 时,即当 时,
△ABC∽ △CDB,∴
⑵∵ ∠1=∠D=90°
∴当 时,即当 时,
△ABC∽ △BDC, ∴
答:略.
1
4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
(3)当△ADE是等腰三角形时,求AE的长
拓展提高
1
2. 把一个等腰直角三角形和一个正三角形分别分割成3个三角形,使等腰直角三角形中的3 个小三角形和正三角形中的3 个小三角形分别相似。请画出三角形的分割线,在小三角形的各个角上标出度数.
画一画:
1、如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
300
300
C
A
B
700
500
E
D
F
700
300
a
b
C
A
B
700
500
E
D
F
700
300
a
b
200
200
性质的应用:
例1、如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过P作PE⊥AB交AC边于点E,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB周长为y,求y与x的函数关系式.
D
Q
A
B
C
P
2. 如图, 边长为4的正方形ABCD中, P是边BC上的一点, QP⊥AP
交 DC于Q, 设
BP= x, △ADQ的面积为y.
(1) 求y与x之间的函数关系式,并求自变量x的取值范围;
(2) 问P点在何位置时,△ADQ的面积最小 最小面积是多少
相似三角形性质应用
3、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m,20m的梯形空地上种植花木(如下图)
(1)他们在△AMD和△BMC地带种植太阳花,单价为8元/m2。当在△AMD地带 (图中阴影部分)中种满花后,共用去了160元。请计算种满△BMC地带所需的费用 是多少元。
(2)若其余地带要种的有玫瑰花和茉莉花两种花木可供选择,单价分别为12元/m2、10元/m2,应选择哪种花木,刚好用完所筹集的资金?
(3)若梯形ABCD为等腰梯形,面积不变(如图2),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌ △DPC,且△APD的面积与△BPC的面积相等,并说明你的理由。
拓展提高
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC
上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长
为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1)△ABC中BC边上高AD= ;
(2)当x= 时,PQ恰好落在BC边上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式
(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
A
A
B
B
C
C
M
M
N
N
P
P
Q
Q
D
D
(图1)
(图2)
C
E
F
D
B
A
C
B
A
D
E
F
G
P
Q
例3:现用一块直角三角形的边角料来加工
一个正方形,已知两直角边AC=30cm,
BC=40cm.甲,乙两种加工方法如图所示,
请你通过计算说明哪种加工方法能使加
工成的正方形面积更大。
5、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
(1)△ABP与△DPE是否相似?请说明理由;
(2)设AP=x DE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;
(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由;
(4)请你探索在点P运动的过程中,△BPE能否成为等腰三角形?如果能,求出AP的长,如果不能,请说明理由。
C
A
B
D
P
E
2
5
x
y
5-x
拓展提高
6.如图,梯形ABCD中 AD∥BC ,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一P,作射线PE⊥PD,与线段AB交于点E.
(1)试确定CP=5时点E的位置;
(2)若设CP=x,BE=y,试写出y关于自变量x的函数关系式,并求出自变量x的取值范围.
提示:体会这个图形的“模型” 作用,将会助你快速解题!
B
C
A
D
E
P
H
C
E
P
A
D
拓展提高
7.如图,已知抛物线与x轴交于A、B
两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足
∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴
上是否存在点E,使得以A、O、E
为顶点的三角形与⊿PBC相似?若
存在,求出点E的坐标;若不存在,
请说明理由.
A
B
P
C
O
x
y
X=4
2
3
Q
6
拓展提高
例4、如图,已知△ABC、△DEF均为等边三角形,点D、E分别在AB、BC上.
如图①当D、E分别在AB、BC中点时,图中有与△DBE相似的三角形吗 请找出,并选一个进行说明.
如图②当D、E分别从AB、BC中点向A、C以相同速度运动时,图中有与△DBE相似的三角形吗 请找出,并选一个进行说明.
如图③当D、E分别是AB、BC上任意一点, ②中的结论是否仍然成立 如果成立,请你找出, 并选一个进行说明.
①
②
③
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠AED=∠B
∵∠A=∠A,∠AED=∠B
∴△AED∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠ADE=∠C
∵∠A=∠A,∠ADE=∠C
∴△AED∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠ADE=∠B
∵∠A=∠A,∠ADE=∠B
∴△ADE∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
∠AED=∠C
∵∠A=∠A,∠AED=∠C
∴△ADE∽△ABC
(有两个角对应相等的两个三角形相似。)
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
AD
AB
-=-
AE
AC
∵∠A=∠A,
∴△ADE∽△ABC
(两边对应成比例,且夹角相等的两个
三角形相似。)
A
E
D
B
C
如图,D、E分别是△ABC的边AB、AC上的点,请你添加一个
条件,使△ABC和△AED相似,你添加的条件是____________.
AD
AC
-=-
AE
AB
∵∠A=∠A,
∴△AED∽△ABC
(两边对应成比例,且夹角相等的两个
三角形相似。)
2.已知如图,D点是不等边 ABC的边AC上一点,过D点画线段DE,使点E在 ABC的边上,并且点D,点E和 ABC的一个顶点组成的小三角形与 ABC相似。问:这样的三角形可以画几个?画出DE,并且写出添线方法(可讨论并答出作图依据)
A
C
. D
B
A
C
. D
B
B
A
C
. D
A
C
. D
B
E
E
E
E
1.过Rt△ABC的斜边AB上一点D作一条直线与另一边AC或者BC相交,使截得的小三角形与△ABC相似,这样的直线有几条?
A
C
D ●
A
B
E
A
B
C
.
1、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2,
在AC上取一点F,使以A、E、F为顶点的三角形与
△ABC相似,那么AF=________
F2
F1
练一练
2.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE相似。
E
A
B
C
D
M
N
1或4
练一练:
3.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
(0,1.5)或(0,2/3)
练一练
C
A
O
B
在Rt△OBC中,已知OB=4,OC=2,OA=1,
求证:△AOC∽△COB
C
A
O
在直线AC上是否存在点M,
使得以A,B,M为顶点的三
角形和△AOC相似,若不存
在,请说明理由.若存在,这样
的M点共有几个 请求出AM
的长。
M
M
OB=4,OC=2,OA=1
B
在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫做格点三角形,如图所示,在10×10的方格中,已知△OAB.
x
y
4
-1
-1
4
3
2
1
3
0
1
2
A
-4
-3
-2
-4
-3
-2
B
5
-5
作一个格点三角形与△OAB相似且与△OAB 共边AB.
●
●
●
●
●
4. 如图,平面直角坐标系中,直线AB与x轴y轴分别A(3,0)B(0, )两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
(1)求直线AB的解析式;
(2)在第一象限内求作一点P,使得以P,O,B为顶点的三角形与⊿OBA相似,并求出所有符合条件的点P.
A
O
D
C
B
y
x
C
A
O
B
x
y
OB=4,OC=2,OA=1
D
过点C作 CD∥x轴,一动点P从
点A出发,以每秒1个单位长度
的速度匀速向B点运动,同时动
点Q从C点出发沿射线CD以每
秒2个单位长度的速度匀速运动,
当P达到B后,运动停止,设运动时间为t.连结PQ交CB于点E。
P
E
(1)经过几秒后,S△CEQ=4S△BPE
(2)在运动过程中,当BE:EC=1:4时,请写出E点的坐标.
Q
你能判断PQ与BC的位置关系吗
1、如图, 已知点P是边长为4的正方形ABCD内的一点,且PB=3,BF⊥BP. 试问在射线BF上是否存在一点E,使以点B、E、C为顶点的三角形与△ABP相似 若存在,请求出BE的长;若不存在,请说明理由.
F
C
A
B
D
P
E
E
相应练习
B
C
A
Q
P
8
16
2cm/秒
4cm/秒
练一练
2、在 ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟 BPQ与 BAC相似?
练一练
3、如图:已知∠ABC=∠CDB=90°,AC=5cm,BC=3cm,当BD取多少cm时 △ABC和△BDC相似?
4
D
A
B
C
5
3
4.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果点P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QPBC的面积,提出一个与计算结果有关的结论;
(3)那么当t为何值时,以点Q、A、P为顶点的三角形和△ABC相似
2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似
D
A
B
C
a
b
解:⑴∵ ∠1=∠D=90°
∴当 时,即当 时,
△ABC∽ △CDB,∴
⑵∵ ∠1=∠D=90°
∴当 时,即当 时,
△ABC∽ △BDC, ∴
答:略.
1
4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
(3)当△ADE是等腰三角形时,求AE的长
拓展提高
1
2. 把一个等腰直角三角形和一个正三角形分别分割成3个三角形,使等腰直角三角形中的3 个小三角形和正三角形中的3 个小三角形分别相似。请画出三角形的分割线,在小三角形的各个角上标出度数.
画一画:
1、如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
300
300
C
A
B
700
500
E
D
F
700
300
a
b
C
A
B
700
500
E
D
F
700
300
a
b
200
200
性质的应用:
例1、如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过P作PE⊥AB交AC边于点E,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB周长为y,求y与x的函数关系式.
D
Q
A
B
C
P
2. 如图, 边长为4的正方形ABCD中, P是边BC上的一点, QP⊥AP
交 DC于Q, 设
BP= x, △ADQ的面积为y.
(1) 求y与x之间的函数关系式,并求自变量x的取值范围;
(2) 问P点在何位置时,△ADQ的面积最小 最小面积是多少
相似三角形性质应用
3、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m,20m的梯形空地上种植花木(如下图)
(1)他们在△AMD和△BMC地带种植太阳花,单价为8元/m2。当在△AMD地带 (图中阴影部分)中种满花后,共用去了160元。请计算种满△BMC地带所需的费用 是多少元。
(2)若其余地带要种的有玫瑰花和茉莉花两种花木可供选择,单价分别为12元/m2、10元/m2,应选择哪种花木,刚好用完所筹集的资金?
(3)若梯形ABCD为等腰梯形,面积不变(如图2),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌ △DPC,且△APD的面积与△BPC的面积相等,并说明你的理由。
拓展提高
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC
上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长
为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1)△ABC中BC边上高AD= ;
(2)当x= 时,PQ恰好落在BC边上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式
(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
A
A
B
B
C
C
M
M
N
N
P
P
Q
Q
D
D
(图1)
(图2)
C
E
F
D
B
A
C
B
A
D
E
F
G
P
Q
例3:现用一块直角三角形的边角料来加工
一个正方形,已知两直角边AC=30cm,
BC=40cm.甲,乙两种加工方法如图所示,
请你通过计算说明哪种加工方法能使加
工成的正方形面积更大。
5、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),PE⊥BP,PE交DC于点E.
(1)△ABP与△DPE是否相似?请说明理由;
(2)设AP=x DE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;
(3)请你探索在点P运动的过程中,四边形ABED能否构成矩形?如果能,求出AP的长;如果不能,请说明理由;
(4)请你探索在点P运动的过程中,△BPE能否成为等腰三角形?如果能,求出AP的长,如果不能,请说明理由。
C
A
B
D
P
E
2
5
x
y
5-x
拓展提高
6.如图,梯形ABCD中 AD∥BC ,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一P,作射线PE⊥PD,与线段AB交于点E.
(1)试确定CP=5时点E的位置;
(2)若设CP=x,BE=y,试写出y关于自变量x的函数关系式,并求出自变量x的取值范围.
提示:体会这个图形的“模型” 作用,将会助你快速解题!
B
C
A
D
E
P
H
C
E
P
A
D
拓展提高
7.如图,已知抛物线与x轴交于A、B
两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足
∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴
上是否存在点E,使得以A、O、E
为顶点的三角形与⊿PBC相似?若
存在,求出点E的坐标;若不存在,
请说明理由.
A
B
P
C
O
x
y
X=4
2
3
Q
6
拓展提高
例4、如图,已知△ABC、△DEF均为等边三角形,点D、E分别在AB、BC上.
如图①当D、E分别在AB、BC中点时,图中有与△DBE相似的三角形吗 请找出,并选一个进行说明.
如图②当D、E分别从AB、BC中点向A、C以相同速度运动时,图中有与△DBE相似的三角形吗 请找出,并选一个进行说明.
如图③当D、E分别是AB、BC上任意一点, ②中的结论是否仍然成立 如果成立,请你找出, 并选一个进行说明.
①
②
③
同课章节目录
