4.6图形的位似

(共21张PPT)
4.6 图形的位似
　　　　
观察思考：这两幅图片有什么特征？
都是有好几张相似图形组成，每个对应顶点都经过一点
　 如果两个图形不仅形状相同，而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形, 这个点叫做位似中心.
显然，位似图形是相似图形的特殊情形，其相似比又叫做它们的位似比.
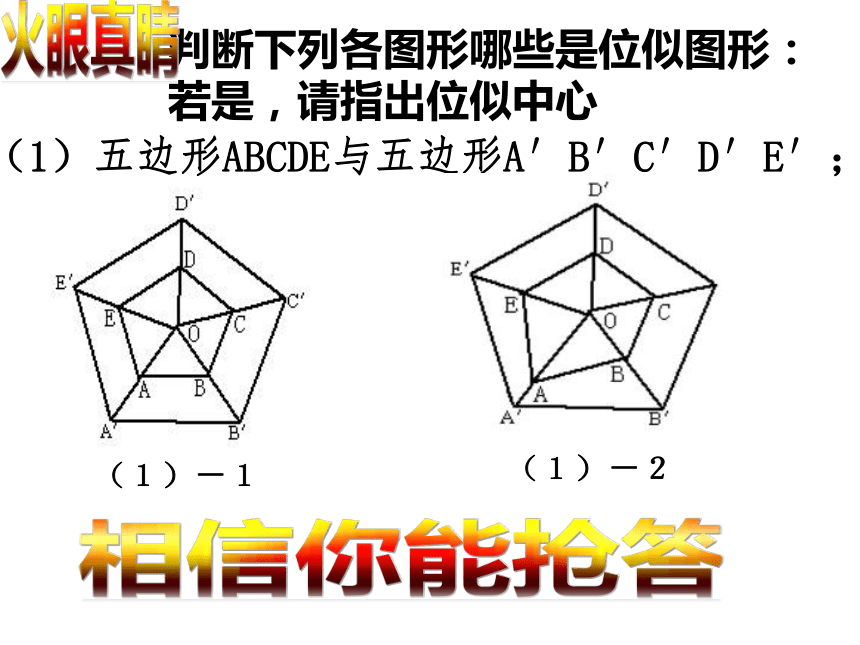
判断下列各图形哪些是位似图形：
若是，请指出位似中心
（1）五边形ABCDE与五边形A′B′C′D′E′；
（１）－１
（１）－２
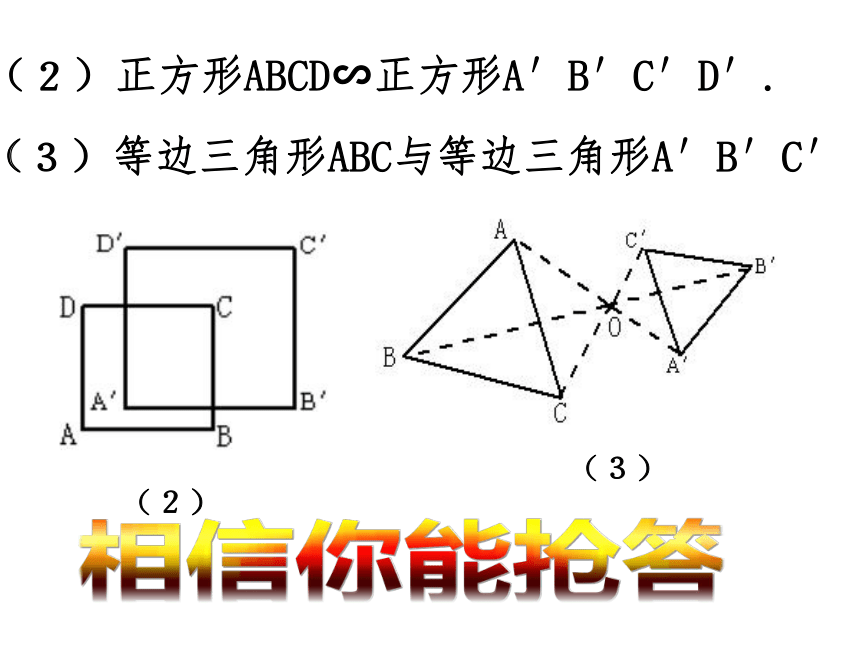
（２）正方形ABCD∽正方形A′B′C′D′.
（３）等边三角形ABC与等边三角形A′B′C′
（２）
（３）
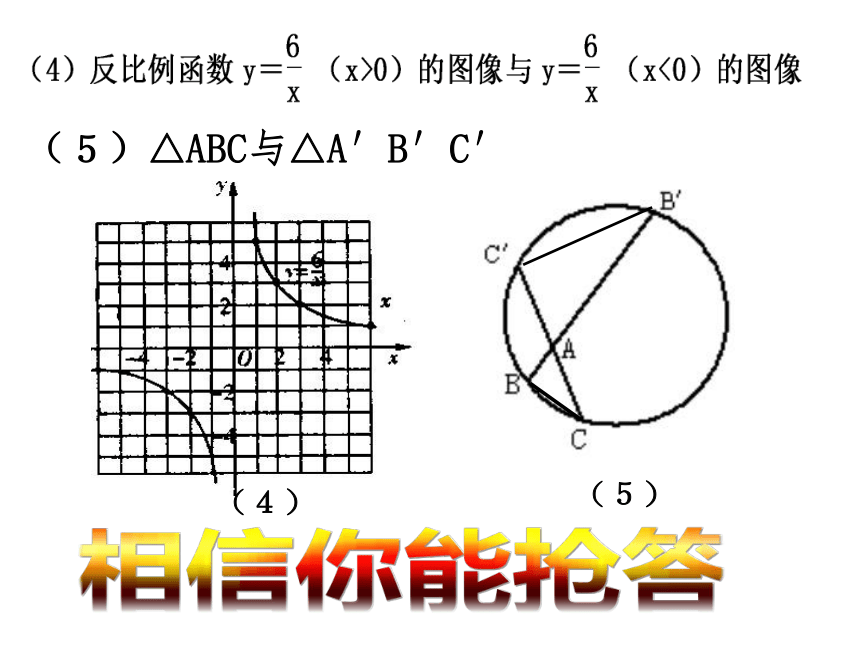
（５）△ABC与△A′B′C′
（４）
（５）
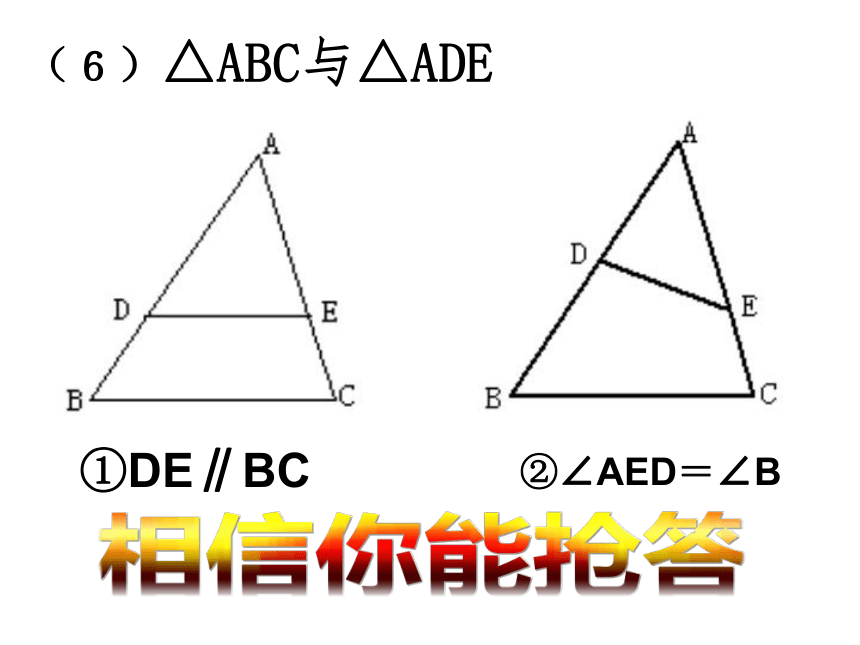
（６）△ABC与△ADE
①DE∥BC
②∠AED＝∠B
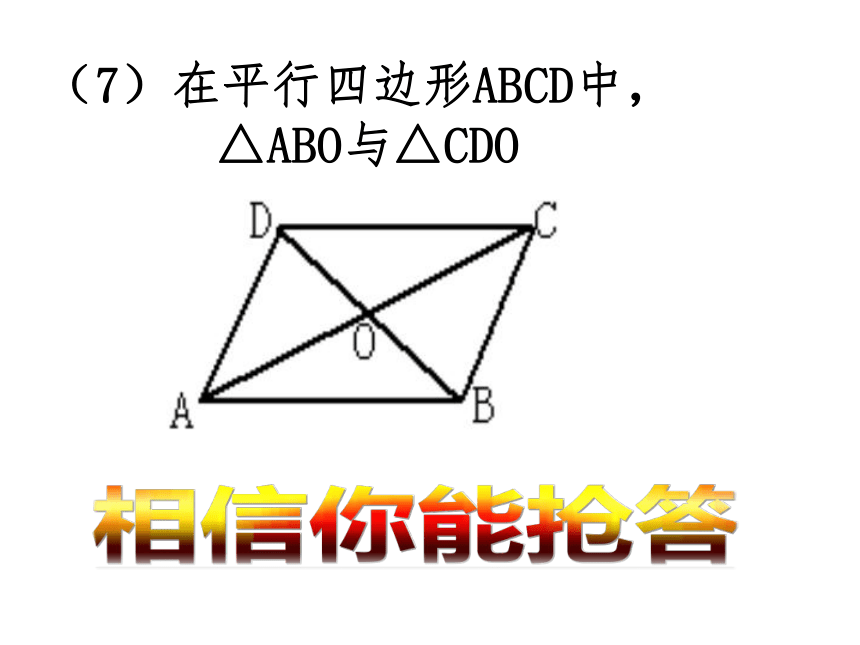
（7）在平行四边形ABCD中， △ABO与△CDO
1．两图形相似．
同时满足下面两个条件的两个
图形才叫做位似图形．两条件缺一不可．
2．每组对应点所在直线都
经过同一点．
　（１）下列位似图形中，每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图，你能猜想对应点到位似中心的距离之比与位似比之间有什么关系？
观察与思考

如图P，E，F分别是AC，AB，AD的中点，四边形AEPF与四边形ABCD是位似图形吗？如果是位似图形，说出位似中心和位似比. 并判断AF:AD=FP:DC
如图：等边三角形ABC与等边三角形A′B′C′
判断AO:A′O=AB:A′B′
一般地，位似图形有以下性质：
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
C′
例.如图，请以坐标原点O为位似中心，作平行四边形ABCD的位似图形，并把它的边长放大2倍.
X
Y
-2
2
4
6
-6
-4
8
-8
-10
10
12
-12
D
A
B
C
12
4
0
2
6
8
10
-2
-4
-6
-8
-10
-12
分析：根据位似图形上任意一对对应点到位似中心的距离之比等于位似比，我们只要连结位似中心O和的各顶点，并把线段延长（或反向延长）到原来的2倍，就得到所求作图形的各个顶点
G
F
E
B′
A′
D′
以坐标原点为位似中心的位似变换有一下性质：
若原图形上点的坐标为（x，y），像与原图形的位似比为k，则像上的对应点的坐标为（kx，ky）或（―kx，―ky）.
想一想：
怎样运用像与原像对应点的坐标关系，画出以原点为位似中心的位似图形？
X
Y
4
2
6
8
10
12
-12 -10 -8 -6 -4 -2 0
-2
2
4
6
-6
-4
8
-8
-10
10
12
-12
D
A
B
C
如图,请以坐标原点O为位似中心，作平行四边形的位似图形，并把它的边长放大３倍．
我的舞台,我出手
　如图，已知△ABC和点O.以O为位似中心，求作△ABC的位似图形，并把△ABC的边长缩小到原来的一半.
我的舞台,我出手
课堂小结：
1、如果两个图形不仅是相似图形，而且是每组对应点所在的直线都经过同一个点， 那么这样的两个图形叫做　　　　　。
2、 这个点叫做　　　　　。
3、这时的相似比又称为　　　　 。
　　4、位似图形上任意一对对应点到位似中
心的距离之比等于　　　　　 。
5. 在以坐标原点为位似中心的位似变换中若原图形上点的坐标为（x，y），像与原图形的位似比为k，则像上的对应点的坐标为（kx，ky）或（―kx，―ky）
6、我学会了把任意图形　　　　　　 。
　　
位似图形
位似中心
位似比
位似比
放大与缩小
如图所示，以点O为位似中心，作出已知图形的3个位似图形，给人以船由远及近的视觉效果。
O