2020-2021学年浙教版九年级数学上册第四章《相似三角形》综合提高A卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级数学上册第四章《相似三角形》综合提高A卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 346.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 22:25:43 | ||
图片预览

文档简介
2020-2021学年浙教版九年级数学第四章《相似三角形》综合提高A卷
班级:
_________
姓名:
_________
成绩
_________
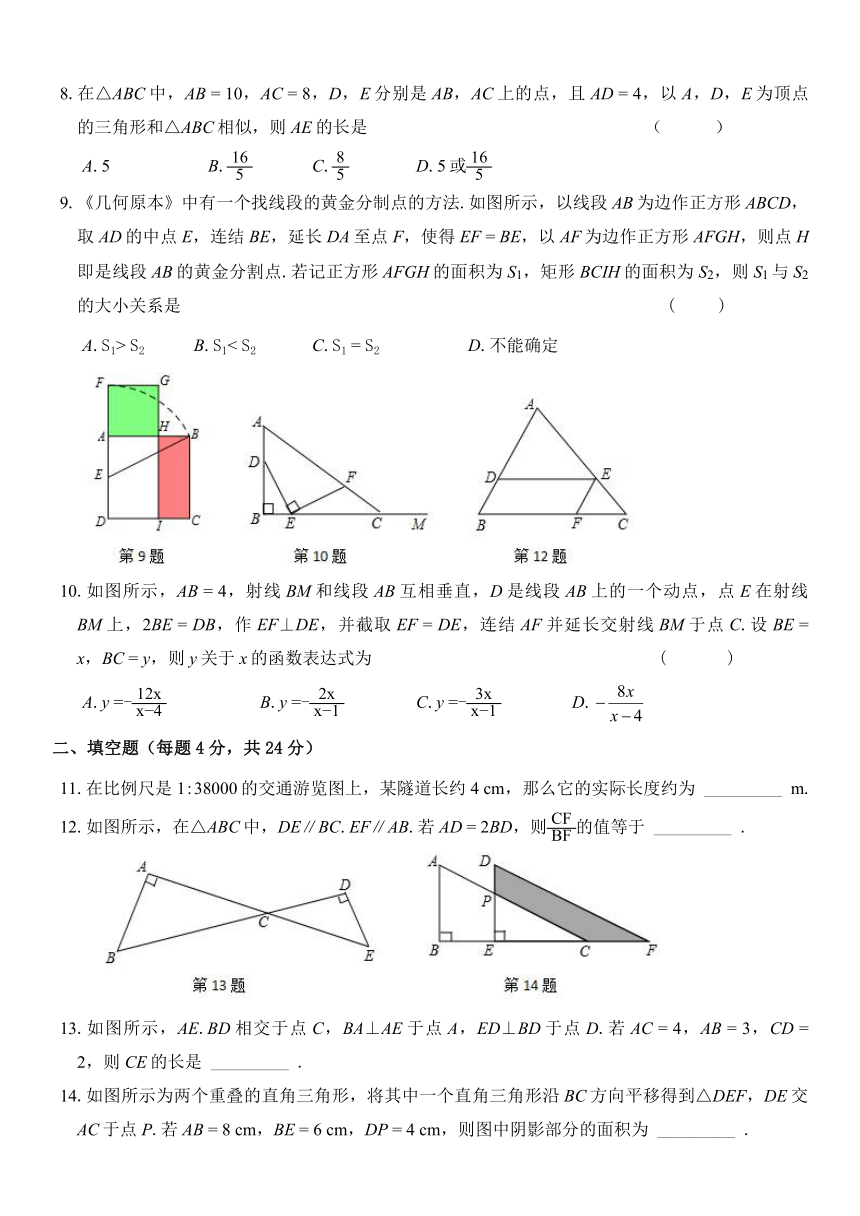
一、选择题(每题3分,共30分)
1.已知△ABC
∽△DEF,相似比为3
:1,且△DEF的周长为18,则△ABC的周长为
(
)
A.3
B.2
C.6
D.54
2.如果2x
=
3y(x,y均不为0),那么下列各式中,正确的是
(
)
A.
=
B.
=
3
C.
=
D.
=
3.下列判断:①全等三角形是相似三角形;②顶角相等的两个等腰三角形相似;③所有的等边三角形都相似:④所有的直角三角形都相似.其中正确的有
(
)
A.1个
B.2个
C.3个
D.4个
4.如图所示,已知l1∥l2∥l3,AB
=
a,BC
=
b,
=
,则的值为
(
)
A.
B.
C.
D.
5.如图所示,△ABC的两条中线BE,CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2等于
(
)
A.1:4
B.2:3
C.1:3
D.1:2
6.如图所示,A,B,C,D,E,F,G,H,K都是方格纸中的格点,为了使△DEM
∽△ABC,则点M应是F,G,H,K四点中的
(
)
A.点F
B.点G
C.点H
D.点K
7.如图所示,已知正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上,如果BC
=
4.△ABC的面积是6,那么这个正方形的边长是
(
)
A.
B.
C.
D.
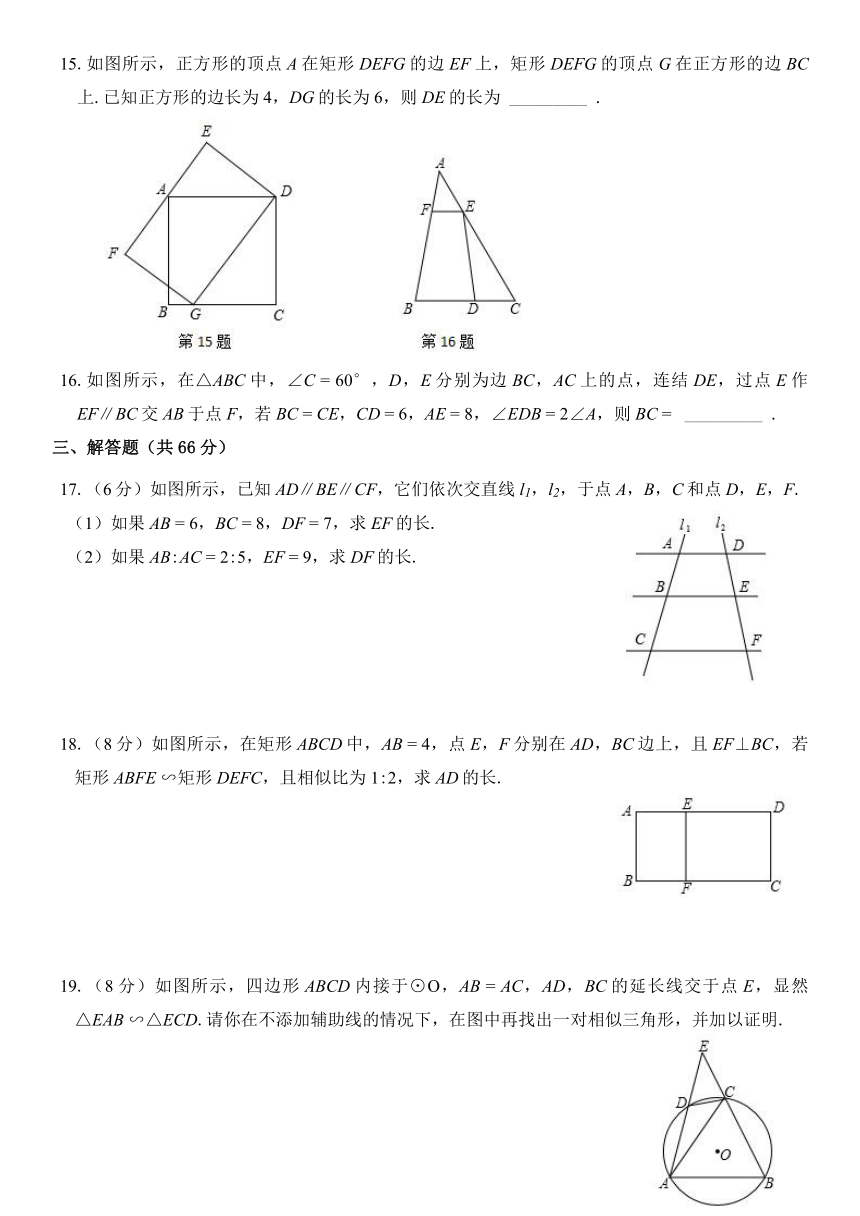
8.在△ABC中,AB
=
10,AC
=
8,D,E分别是AB,AC上的点,且AD
=
4,以A,D,E为顶点的三角形和△ABC相似,则AE的长是
(
)
A.5
B.
C.
D.5或
9.《几何原本》中有一个找线段的黄金分制点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至点F,使得EF
=
BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1与S2的大小关系是
(
)
A.S1>
S2
B.S1<
S2
C.S1
=
S2
D.不能确定
10.如图所示,AB
=
4,射线BM和线段AB互相垂直,D是线段AB上的一个动点,点E在射线BM上,2BE
=
DB,作EF⊥DE,并截取EF
=
DE,连结AF并延长交射线BM于点C.设BE
=
x,BC
=
y,则y关于x的函数表达式为
(
)
A.y
=-
B.y
=-
C.y
=-
D.
二、填空题(每题4分,共24分)
11.在比例尺是1:38000的交通游览图上,某隧道长约4
cm,那么它的实际长度约为
_________
m.
12.如图所示,在△ABC中,DE∥BC.EF∥AB.若AD
=
2BD,则的值等于
_________
.
13.如图所示,AE.BD相交于点C,BA⊥AE于点A,ED⊥BD于点D.若AC
=
4,AB
=
3,CD
=
2,则CE的长是
_________
.
14.如图所示为两个重叠的直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,DE交AC于点P.若AB
=
8
cm,BE
=
6
cm,DP
=
4
cm,则图中阴影部分的面积为
_________
.
15.如图所示,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上.已知正方形的边长为4,DG的长为6,则DE的长为
_________
.
16.如图所示,在△ABC中,∠C
=
60°,D,E分别为边BC,AC上的点,连结DE,过点E作EF∥BC交AB于点F,若BC
=
CE,CD
=
6,AE
=
8,∠EDB
=
2∠A,则BC
=
_________
.
三、解答题(共66分)
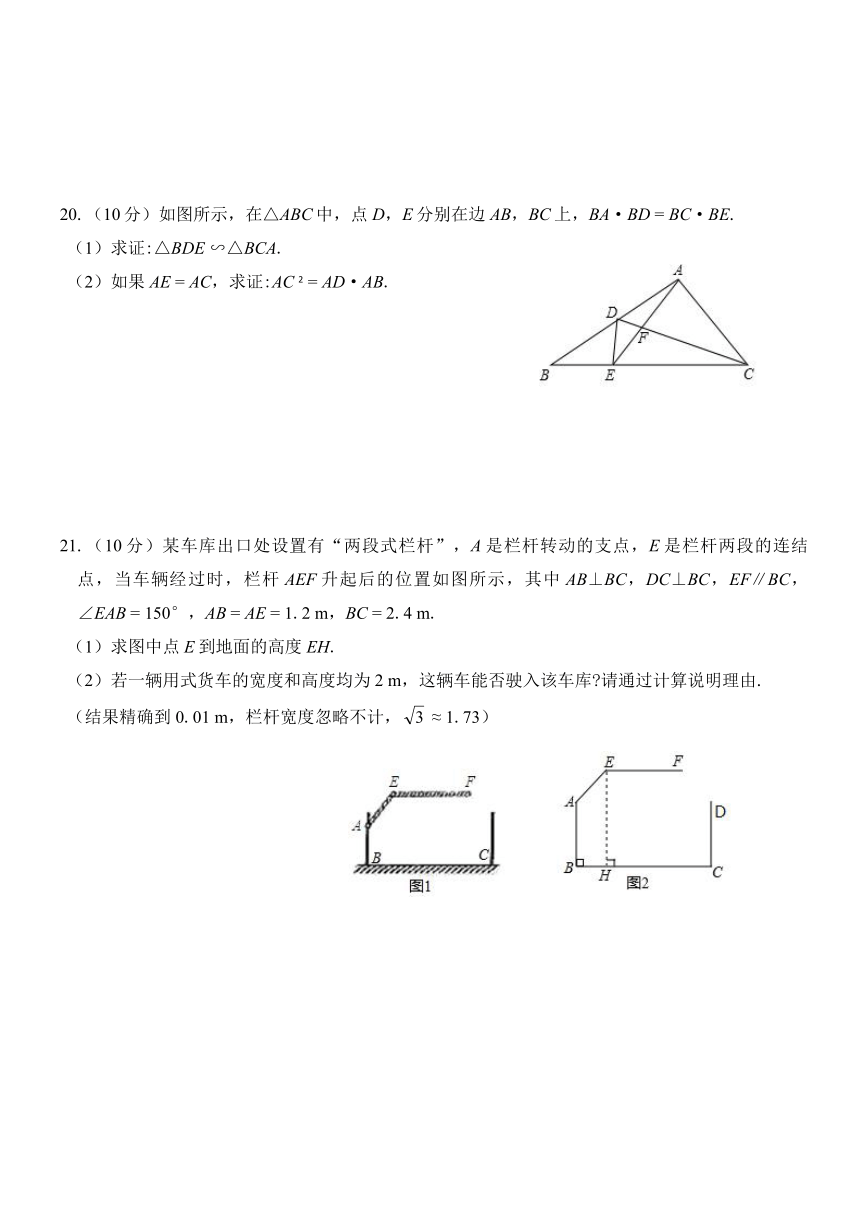
17.(6分)如图所示,已知AD∥BE∥CF,它们依次交直线l1,l2,于点A,B,C和点D,E,F.
(1)如果AB
=
6,BC
=
8,DF
=
7,求EF的长.
(2)如果AB:AC
=
2:5,EF
=
9,求DF的长.
18.(8分)如图所示,在矩形ABCD中,AB
=
4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE
∽矩形DEFC,且相似比为1:2,求AD的长.
19.(8分)如图所示,四边形ABCD内接于⊙O,AB
=
AC,AD,BC的延长线交于点E,显然△EAB
∽△ECD.请你在不添加辅助线的情况下,在图中再找出一对相似三角形,并加以证明.
20.(10分)如图所示,在△ABC中,点D,E分别在边AB,BC上,BA·BD
=
BC·BE.
(1)求证:△BDE
∽△BCA.
(2)如果AE
=
AC,求证:AC
2
=
AD·AB.
21.(10分)某车库出口处设置有“两段式栏杆”,A是栏杆转动的支点,E是栏杆两段的连结点,当车辆经过时,栏杆AEF升起后的位置如图所示,其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB
=
150°,AB
=
AE
=
1.2
m,BC
=
2.4
m.
(1)求图中点E到地面的高度EH.
(2)若一辆用式货车的宽度和高度均为2
m,这辆车能否驶入该车库?请通过计算说明理由.
(结果精确到0.01
m,栏杆宽度忽略不计,
≈
1.73)
(12分)如图所示,已知△ABC
∽△A1B2C3,相似比为k(k
>
1),且△ABC的三边长分别为a,b,c(a
>
b
>
c),△A1B1C1的三边长分别为a1,b1,c1
_________
(1)若c
=
a1,求证:a
=
kc.
(2)若c
=
a1,试给出符合条件的一财△ABC和△A1B1C1,使得a,b,c和a1,b1,c1都是正整数,并加以说明.
(3)若b
=
a1,c
=
b1,是否存在△ABC和△A1B1C1使得k
=
2?请说明理由.
23.(12分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,那么我们就把这条线段叫做这个三角形的“完美分割线”.
(1)如图1所示,在△ABC中,CD为角平分线,∠A
=
40°,∠B
=
60°,求证:CD为△ABC的“完美分割线”
(2)在△ABC中,∠A
=
48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2所示,在△ABC中,AC
=
2,BC
=
,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
班级:
_________
姓名:
_________
成绩
_________
一、选择题(每题3分,共30分)
1.已知△ABC
∽△DEF,相似比为3
:1,且△DEF的周长为18,则△ABC的周长为
(
)
A.3
B.2
C.6
D.54
2.如果2x
=
3y(x,y均不为0),那么下列各式中,正确的是
(
)
A.
=
B.
=
3
C.
=
D.
=
3.下列判断:①全等三角形是相似三角形;②顶角相等的两个等腰三角形相似;③所有的等边三角形都相似:④所有的直角三角形都相似.其中正确的有
(
)
A.1个
B.2个
C.3个
D.4个
4.如图所示,已知l1∥l2∥l3,AB
=
a,BC
=
b,
=
,则的值为
(
)
A.
B.
C.
D.
5.如图所示,△ABC的两条中线BE,CD相交于点O,记△DOE的面积为S1,△COB的面积为S2,则S1:S2等于
(
)
A.1:4
B.2:3
C.1:3
D.1:2
6.如图所示,A,B,C,D,E,F,G,H,K都是方格纸中的格点,为了使△DEM
∽△ABC,则点M应是F,G,H,K四点中的
(
)
A.点F
B.点G
C.点H
D.点K
7.如图所示,已知正方形DEFG的顶点D,E在△ABC的边BC上,顶点G,F分别在边AB,AC上,如果BC
=
4.△ABC的面积是6,那么这个正方形的边长是
(
)
A.
B.
C.
D.
8.在△ABC中,AB
=
10,AC
=
8,D,E分别是AB,AC上的点,且AD
=
4,以A,D,E为顶点的三角形和△ABC相似,则AE的长是
(
)
A.5
B.
C.
D.5或
9.《几何原本》中有一个找线段的黄金分制点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至点F,使得EF
=
BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1与S2的大小关系是
(
)
A.S1>
S2
B.S1<
S2
C.S1
=
S2
D.不能确定
10.如图所示,AB
=
4,射线BM和线段AB互相垂直,D是线段AB上的一个动点,点E在射线BM上,2BE
=
DB,作EF⊥DE,并截取EF
=
DE,连结AF并延长交射线BM于点C.设BE
=
x,BC
=
y,则y关于x的函数表达式为
(
)
A.y
=-
B.y
=-
C.y
=-
D.
二、填空题(每题4分,共24分)
11.在比例尺是1:38000的交通游览图上,某隧道长约4
cm,那么它的实际长度约为
_________
m.
12.如图所示,在△ABC中,DE∥BC.EF∥AB.若AD
=
2BD,则的值等于
_________
.
13.如图所示,AE.BD相交于点C,BA⊥AE于点A,ED⊥BD于点D.若AC
=
4,AB
=
3,CD
=
2,则CE的长是
_________
.
14.如图所示为两个重叠的直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF,DE交AC于点P.若AB
=
8
cm,BE
=
6
cm,DP
=
4
cm,则图中阴影部分的面积为
_________
.
15.如图所示,正方形的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形的边BC上.已知正方形的边长为4,DG的长为6,则DE的长为
_________
.
16.如图所示,在△ABC中,∠C
=
60°,D,E分别为边BC,AC上的点,连结DE,过点E作EF∥BC交AB于点F,若BC
=
CE,CD
=
6,AE
=
8,∠EDB
=
2∠A,则BC
=
_________
.
三、解答题(共66分)
17.(6分)如图所示,已知AD∥BE∥CF,它们依次交直线l1,l2,于点A,B,C和点D,E,F.
(1)如果AB
=
6,BC
=
8,DF
=
7,求EF的长.
(2)如果AB:AC
=
2:5,EF
=
9,求DF的长.
18.(8分)如图所示,在矩形ABCD中,AB
=
4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE
∽矩形DEFC,且相似比为1:2,求AD的长.
19.(8分)如图所示,四边形ABCD内接于⊙O,AB
=
AC,AD,BC的延长线交于点E,显然△EAB
∽△ECD.请你在不添加辅助线的情况下,在图中再找出一对相似三角形,并加以证明.
20.(10分)如图所示,在△ABC中,点D,E分别在边AB,BC上,BA·BD
=
BC·BE.
(1)求证:△BDE
∽△BCA.
(2)如果AE
=
AC,求证:AC
2
=
AD·AB.
21.(10分)某车库出口处设置有“两段式栏杆”,A是栏杆转动的支点,E是栏杆两段的连结点,当车辆经过时,栏杆AEF升起后的位置如图所示,其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB
=
150°,AB
=
AE
=
1.2
m,BC
=
2.4
m.
(1)求图中点E到地面的高度EH.
(2)若一辆用式货车的宽度和高度均为2
m,这辆车能否驶入该车库?请通过计算说明理由.
(结果精确到0.01
m,栏杆宽度忽略不计,
≈
1.73)
(12分)如图所示,已知△ABC
∽△A1B2C3,相似比为k(k
>
1),且△ABC的三边长分别为a,b,c(a
>
b
>
c),△A1B1C1的三边长分别为a1,b1,c1
_________
(1)若c
=
a1,求证:a
=
kc.
(2)若c
=
a1,试给出符合条件的一财△ABC和△A1B1C1,使得a,b,c和a1,b1,c1都是正整数,并加以说明.
(3)若b
=
a1,c
=
b1,是否存在△ABC和△A1B1C1使得k
=
2?请说明理由.
23.(12分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,那么我们就把这条线段叫做这个三角形的“完美分割线”.
(1)如图1所示,在△ABC中,CD为角平分线,∠A
=
40°,∠B
=
60°,求证:CD为△ABC的“完美分割线”
(2)在△ABC中,∠A
=
48°,CD是△ABC的“完美分割线”,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2所示,在△ABC中,AC
=
2,BC
=
,CD是△ABC的“完美分割线”,且△ACD是以CD为底边的等腰三角形,求“完美分割线”CD的长.
同课章节目录
