2.6 探索勾股定理（1）

(共16张PPT)
2.6探索勾股定理(1)
A
B
C
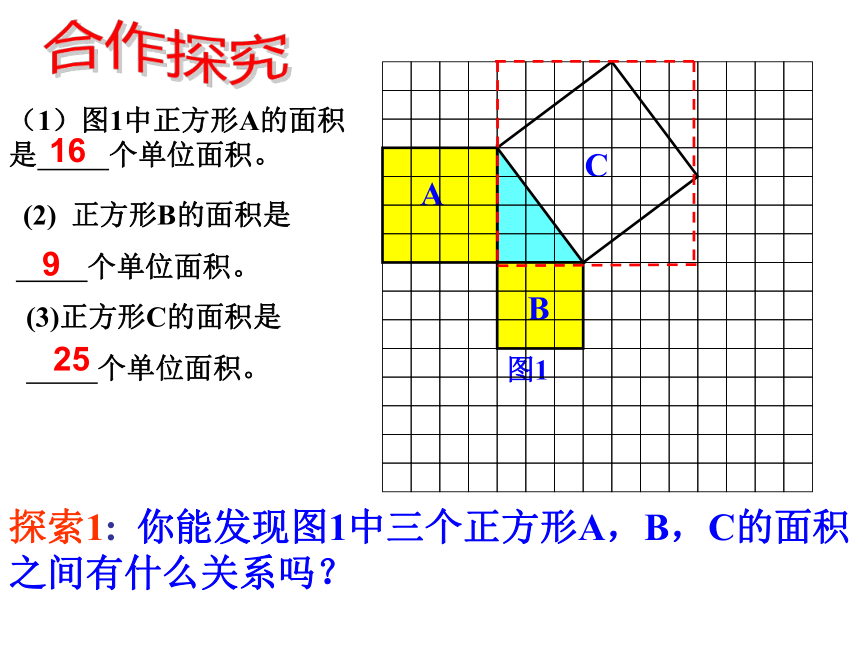
图1
（1）图1中正方形A的面积是 个单位面积。
(2) 正方形B的面积是
个单位面积。
(3)正方形C的面积是
个单位面积。
16
9
25
探索1: 你能发现图1中三个正方形A，B，C的面积之间有什么关系吗？
A
B
C
图1-1
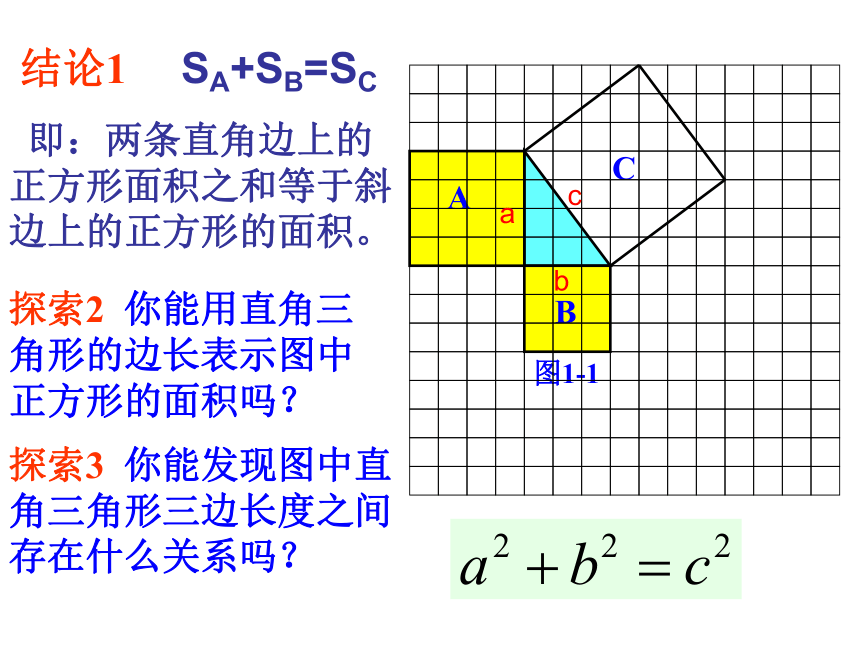
结论1 SA+SB=SC
探索2 你能用直角三角形的边长表示图中正方形的面积吗？
探索3 你能发现图中直角三角形三边长度之间存在什么关系吗？
a
c
b
即：两条直角边上的正方形面积之和等于斜边上的正方形的面积。
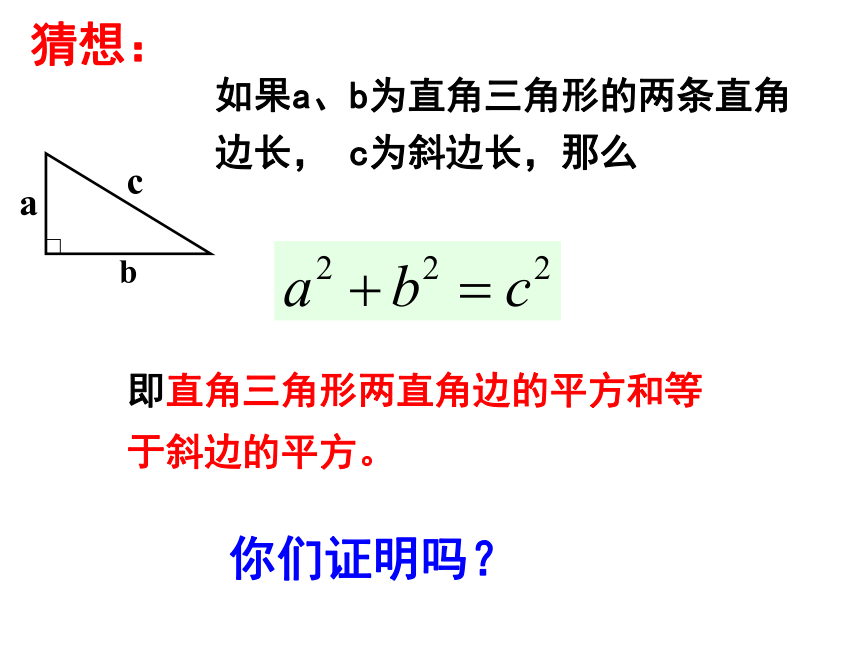
猜想：
如果a、b为直角三角形的两条直角边长， c为斜边长，那么
a
b
c
即直角三角形两直角边的平方和等于斜边的平方。
你们证明吗？
a
b
c
c
a
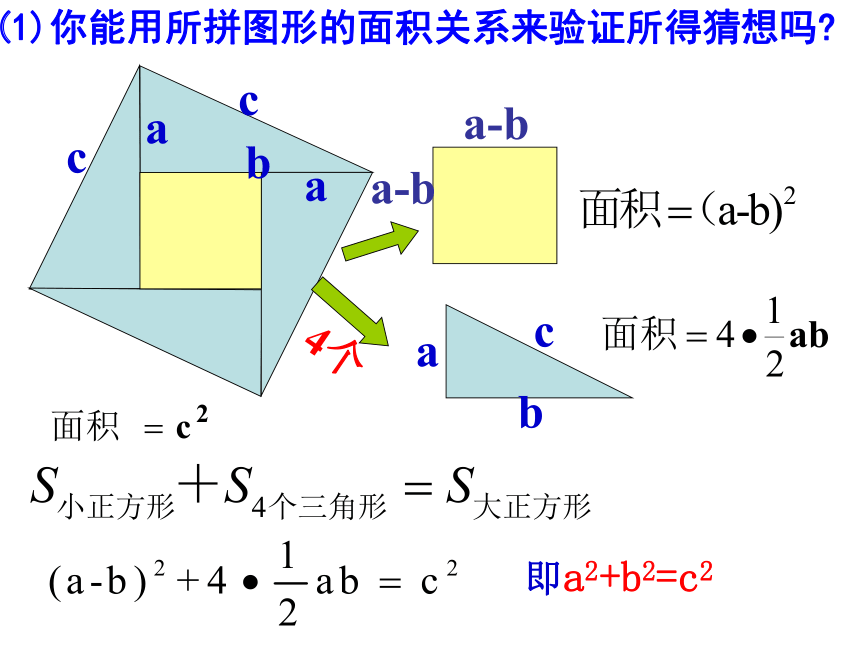
即a2+b2=c2
a
b
c
4个
a-b
a-b
(1)你能用所拼图形的面积关系来验证所得猜想吗
即a2+b2=c2
c
c
a
b
c
4个
b
a
c
a
b
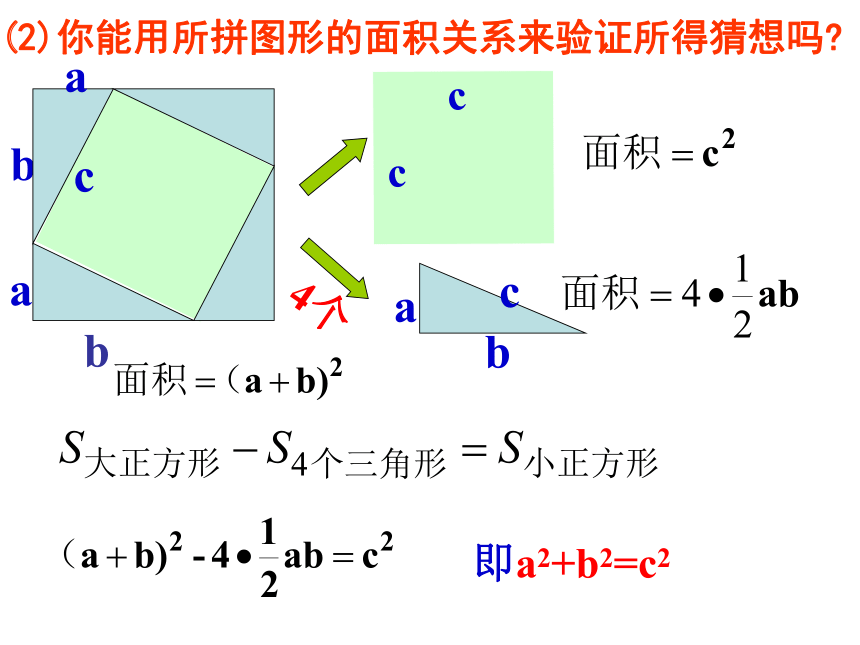
(2)你能用所拼图形的面积关系来验证所得猜想吗
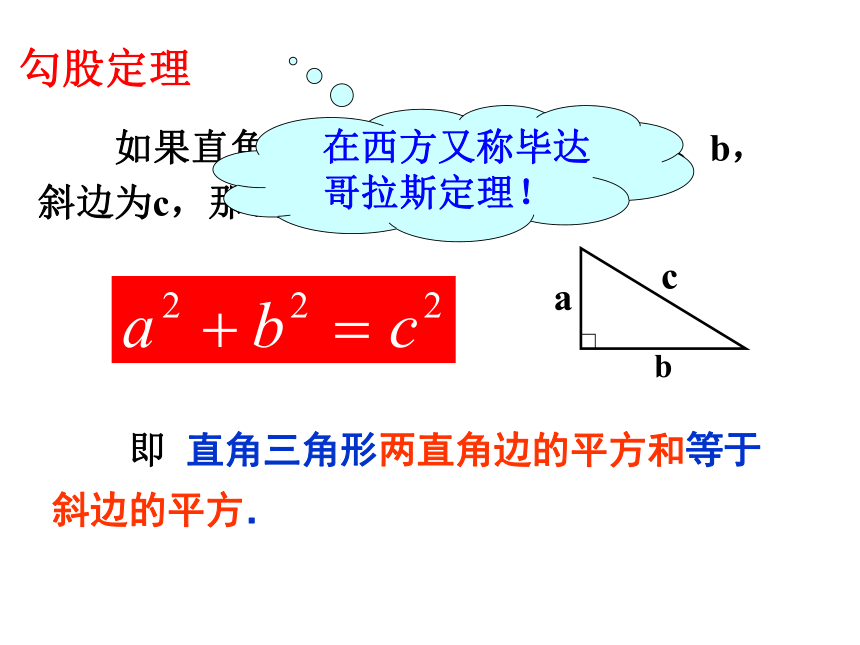
勾股定理
　　如果直角三角形两直角边分别为a、b，斜边为c，那么
　　即 直角三角形两直角边的平方和等于斜边的平方．
a
b
c
在西方又称毕达哥拉斯定理！
例1:已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
已知: a=15, b:c=8:17, 求b,c;
a
b
c
解:(1)根据勾股定理得:
c2=a2+b2
∵c>0, ∴c=
=12 +22 =5
(2)设a＝8x，则b＝17x(x>0)
∵a2+b2=c2
∴ (17x)2-(8x)2=152
∴ x2=1
∵x>0,
∴x=1
∴ a＝8，b＝17
(1)直角三角形的两直角边为3和4,则斜边为___
(2)直角三角形的两条边为3和4，则这个直角三角形的周长为 。
12
或
P40课内练习1.
例2：一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.
A
B
90
160
40
40
C
解：过A作铅垂线，
过B作水平线,两线交于点C，则∠ACB=90°
AC=90-40=50(mm)
由勾股定理，得
∵AB﹥0， ∴AB=130(mm)
答：两孔中心A、B之间的距离为130mm。
构造直角三角形可 以解决实际问题。
BC=160-40=120(mm)
50
120
P40作业题4,7
(1)求墙的高度
解：
∴AC=
∵∠ACB=90°AB=2.5，BC=0.7
=
=2.4(米)
(2)若梯子的顶端下滑40厘米,
底端将向外水平移动多少米
请说明理由
A
A′
B
B′
2.5m
0.7m
C
∴ AB2=AC2+BC2
有一架2.5米长的梯子靠在学校围墙上,刚好与墙头对齐时梯脚B与墙脚C的距离是0.7米。
如图，在△ABC中，AB=AC。已知AB=17，BC=16。
(1)求BC边上的中线AD的长。
(2)求△ABC的面积。
(3)过点B作BE⊥AC，垂足为E，求BE的长。
E
P40作业题6
x
例3：(1)求出下列x的值
2
-1
0
1
2
1
x
0
2
（3）利用作直角三角形，在数轴上表示
2
3
(2)你能参考下图在数轴上准确表示 吗？
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
7cm
2．如图，所有的四边形都是正方形，所有的三角形
都是直角三角形，其中最大的正方形的边长为7cm,则
正方形A，B，C，D的面积之和为___________cm2。
49
A
D
C
B
3.做一个长，宽，高分别为50厘米，40厘米，30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明。