2020年秋浙教版八年级数学上册第5章 一次函数单元培优测试卷(word含解析)
文档属性
| 名称 | 2020年秋浙教版八年级数学上册第5章 一次函数单元培优测试卷(word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览


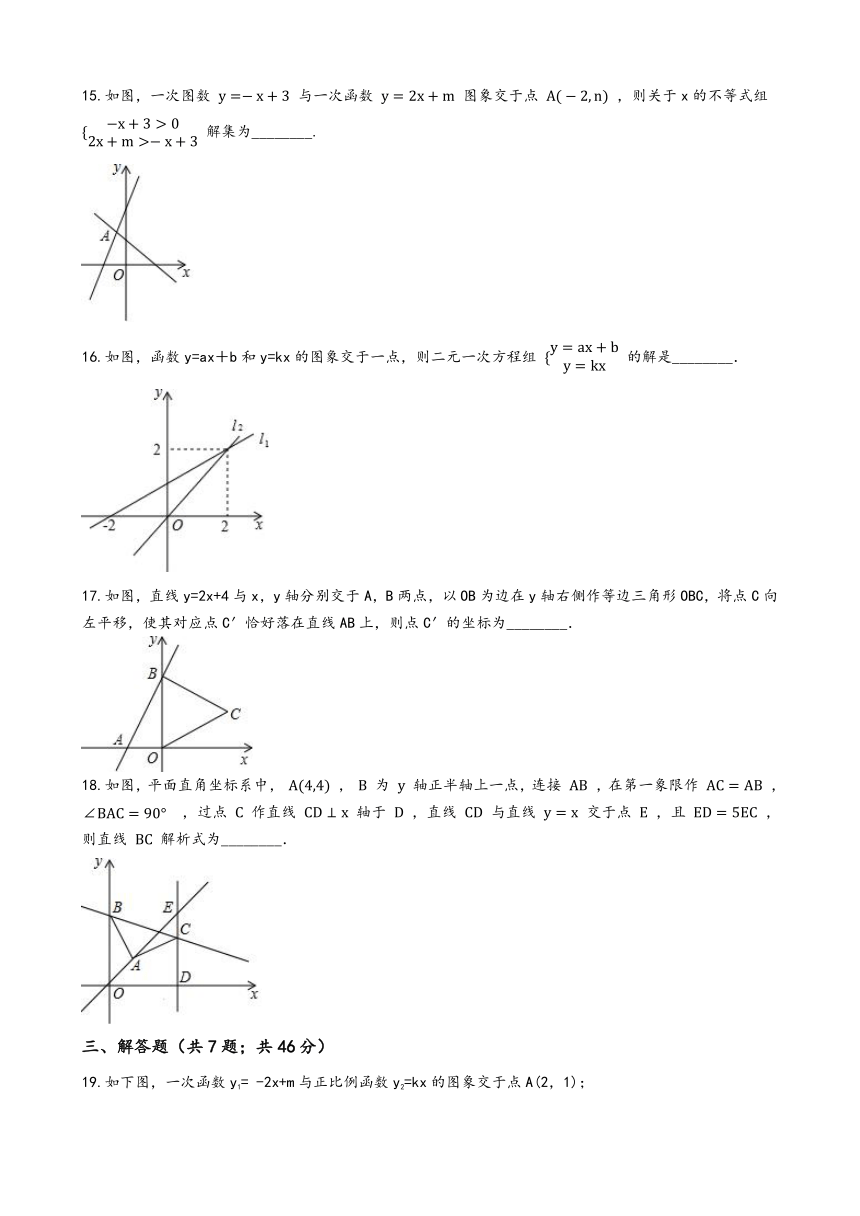


文档简介
2020年秋浙教版八年级数学上册第5章
一次函数单元培优测试卷
一、选择题(共10题;共30分)
1.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是(???
)
A.?数100和n,t都是常量??
B.?数100和N都是变量???????
C.?n和t都是变量???????
D.?数100和t都是变量
2.均匀地向一个容器注水,最后将容器注满,在注水的过程中,水的高度h随时间t的变化如图所示,这个容器的形状可能是(??
)
A.???B.??????C.?????D.?
3.下列图象能表示y是x的函数的是(???
)
A.?B.??C.??D.?
4.在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度
y(cm)与所挂物体的质量
x(kg)之间有如下表关系:
下列说法错误的是(???
)
A.?y
随
x
的增大而增大???B.?所挂物体质量每增加
1kg弹簧长度增加
0.5cm
C.?所挂物体为
7kg时,弹簧长度为
13.5cm?D.?不挂重物时弹簧的长度为
0cm
5.点
在函数
的图像上,则代数式
的值等于(??
)
A.?5???B.?3?????C.?-3????D.?-1
6.已知一次函数
和
的图象都经过A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是(??
)
A.?2?????B.?3???????C.?4?????D.?5
7.平面直角坐标系中,过点(-2,3)的直线
经过一、二、三象限,若点(0,a),(-1,b),(c,-1)都在直线
上,则下列判断正确的是(??
)
A.??????B.????C.??????D.?
8.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是(???
)
A.???B.?????C.?????D.?
且
9.甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同的路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇,在此过程中,两车的距离y(km)与乙车行驶的时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度为120km/h;②m=160;③H点的坐标为(7,80);④n=7.4,其中正确的说法个数为(??
)
A.?1??????B.?2?????C.?3??????D.?4
10.如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是(??
)
A.?8000cm3???B.?10000
cm3???C.?2000πcm3????D.?3000πcm3
二、填空题(共8题;共24分)
11.已知一次函数y=2x-a与y=3x+b的图象交于x轴上原点外的一点,则
=________.
12.已知一次函数
,函数值
随自变量
的值增大而减小,那么
的取值范围是________.
13.小红在练习仰卧起坐,本月
日至
日的成绩与日期具有如下关系:?
日期
(日)
1
2
3
4
成绩
(个)
小红的仰卧起坐成绩y与日期
之间近似为一次函数关系,则该函数表达式为________.
14.若一次函数
的图象经过点
,则
________.
15.如图,一次图数
与一次函数
图象交于点
,则关于x的不等式组
解集为________.
16.如图,函数y=ax+b和y=kx的图象交于一点,则二元一次方程组
的解是________.
17.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为________.
18.如图,平面直角坐标系中,
,
为
轴正半轴上一点,连接
,在第一象限作
,
,过点
作直线
轴于
,直线
与直线
交于点
,且
,则直线
解析式为________.
三、解答题(共7题;共46分)
19.如下图,一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>
y2
,
?
请直接写出x的取值范围.
20.我市人民医院准备从医疗器械销售公司采购A、B两种医疗器械共80件,其中A种器械不少于40件,B种医疗器械的数量不少于A种器械的
,
已知A种器械的售价为每件360元,B种器械的售价为每件400元。
(1)请写出人民医院在这次采购中所需资金y(元)与采购A种医疗器械x(件)的函数解析式,并写出自交量x的取位范围;
(2)为了积极应对本次新冠肺炎疫情,人民医院拿出27000元经费用于采购这80件医疗器械,请问经费是否够用,如果不够)至少还需要经费多少元?
21.已知函数y=2x-6.
(1)当x=2时,求y的值;
(2)当y=
时,求8x-12的值。
22.如图,在平面直角坐标系xOy中,一次函数
的图象经过点A(-2,4),且与正比例函数
的图象交于点B(a,2).
?
(1)求a的值及一次函数
的解析式;
(2)若一次函数
的图象与x轴交于点C,且正比例函数
的图象向下平移m(m>0)个单
位长度后经过点C,求m的值;
(3)直接写出关于x的不等式
的解集.
23.直线AB与y轴交于点B(0,﹣2),且图象过点(2,2).
(1)求直线AB的关系式;
(2)求直线AB与x轴的交点A的坐标;
(3)求△ABO的面积;
(4)求△ABO的周长.
24.团结奋战,众志成城,齐齐哈尔市组织援助医疗队,分别乘甲、乙两车同时出发,沿同一路线赶往绥芬河.齐齐哈尔距绥芬河的路程为800km
,
在行驶过程中乙车速度始终保持80km/h
,
甲车先以一定速度行驶了500km
,
用时5h
,
然后再以乙车的速度行驶,直至到达绥芬河(加油、休息时间忽略不计).甲、乙两车离齐齐哈尔的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:
(1)甲车改变速度前的速度是________km/h
,
乙车行驶________h到达绥芬河;
(2)求甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式,不用写出自变量x的取值范围;
(3)甲车到达绥芬河时,乙车距绥芬河的路程还有________km;出发________h时,甲、乙两车第一次相距40km
.
25.小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段
表示小华和商店的距离
(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(1)填空:妈妈骑车的速度是________米/分钟,妈妈在家装载货物所用时间是________分钟,点M的坐标是________;
(2)直接写出妈妈和商店的距离
(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;
(3)求t为何值时,两人相距360米.
答案
一、选择题
1.解:数100是常量,t,n是变量,故ABD不符合题意,C符合题意.
故答案为:C.
2.解:注水量一定,函数图象的走势是稍陡,平,陡;那么高度就相应的变化,跟所给容器的粗细有关.则相应的排列顺序就为B.
故答案为:B.
3.A.如图,
,对于该x的值,有两个y值与之对应,不是函数图象;
B.如图,
,对于该x的值,有两个y值与之对应,不是函数图象;
C.如图,
对于该x的值,有两个y值与之对应,不是函数图象;
D.对每一个x的值,都有唯一确定的y值与之对应,是函数图象.
故答案为:D.
4.解:由表格可得,弹簧的长度
y(cm)与所挂物体的质量
x(kg)之间的函数关系式为:
A.
,故y随x的增大而增大,故本选项不符合题意;
B.当
时,
;当
时,
,此时
,故本选项不符合题意;
C.当
时,
,故本选项不符合题意;
D.当
时,
,故本选项符合题意.
故答案为:D
5.把
代入函数解析式
得:
,
化简得到:
,
∴
.
故答案为:C.
6.∵一次函数
和
的图象都经过A(-2,0),
∴
,
∴
,
∴两函数表达式分别为
和
,
∴直线
与直线
与
轴的交点分别为B(0,3),C(0,-1),
∴S△ABC
BC?AO
×
×2=4.
故答案为:C.
7.解法1:根据直线l经过第一、二、三象限且过点(-2,3),所以y随x的增大而增大.因为
,所以
,所以A、B、C均错;又因点(c,-1)在直线l上,所以c<-2.
解法2:过点(-2,3)作出草图,再将点(0,a),(-1,b),(c,-1)描出,即可.
故答案为:D.
8.∵
,
∴当y=0时,x=
;当x=0时,y=2t+2,
∴直线
与x轴的交点坐标为(
,0),与y轴的交点坐标为(0,2t+2),
∵t>0,
∴2t+2>2,
当t=
时,2t+2=3,此时
=-6,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图1,
当t=2时,2t+2=6,此时
=-3,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图2,
当t=1时,2t+2=4,
=-4,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,如图3,
∴
且
,
故答案为:D.
9.解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,
∴乙的速度为120km/h.①正确;
∵第2?6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,
∴此时甲乙距离4×40=160km,
∴m=160,②正确;
∵当乙在B休息1h时,甲前进80km,
∴H点坐标为(7,80),③正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,
∴n=6+1+0.4=7.4,④正确;
正确结论的序号为:①②③④.
故答案为:D.
10.解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
∴正方体的棱长为10cm;
∴正方体的体积为:103=1000cm3
设注水的速度为xcm3/s,圆柱的底面积为scm2
,
根据题意得:
解得:
∴圆柱形水槽的容积为:400×20=8000
cm3.
故答案为:A.
二、填空题
11.解:在一次函数y=2x?a中,令y=0,得到x=
,
在一次函数y=3x+b中,令y=0,得到x=?
,
由题意得:
=?
,图象交于x轴上原点外一点,则a≠0,且b≠0,
可以设
=?
=k,则a=2k,b=?3k,
代入
=?2.
故答案为?2.
12.解:∵函数值y随自变量x的值增大而减小,
∴1-2m<0,
∴m>.
故答案为:m>.
13.解:设y=kx+b,
根据题意得
,
解得
,
∴y与x的函数表达式为y=3x+37.
故答案为:
y=3x+37.
14.解:将(3,m)代入y=2x+2中,得2×3+2=m,
解得m=8.
故答案为:8.
15.解:当
时,
,解得
,则一次函数
与x轴的交点坐标为
,
一次图数
与一次函数
图象交于点
,
关于x的不等式组
的解集为
.
故答案为
.
16.解:由图知,函数y=ax+b和y=kx的图象交于点(2,2),
∴二元一次方程组
的解是
,
故答案为:
.
17.∵直线y=2x+4与y轴交于B点,
∴x=0时,
得y=4,
∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴C在线段OB的垂直平分线上,
∴C点纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,
解得x=﹣1.
所以C′的坐标为(﹣1,2).
18.解:过
作
轴,交
轴于
,交
于
,则
,
,
,
,
,
,
,
,
在
和
中,
,
,
,
,
,
设
,
,
,
点
在直线
上,
,
则
,
,即
,
.
点
在直线
上,
,
,
,
,
,
设直线
的解析式是
,
把
代入得:
,
即直线
的解析式是
,
故答案为:
.
三、解答题
19.
(1)解:∵
一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1)
∴-4+m=1,2k=1
解之:m=5,;
(2)
解:(2)∵一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1)
当x<2时,直线y1=
-2x+5m高于直线
y2=x
,即y1>
y2.
20.
(1)解:由题意得:y=360x+400(80-x)=-40x+32000.
∵A种器械不少于40件,B种医疗器械的数量不少于A种器械的,
∴
解之:40≤x≤50
∴x的取值范围是40≤x≤50.
(2)解:∵x的取值范围是40≤x≤50
当x=40时,y=30400
当x=50时,y=30000
∴y的取值范围是:30000≤y≤30400.
所以经费不够用,至少还需要30000-27000=3000元.
答:经费不够用,至少还需要3000元.
21.
(1)解:将x=2,代入y=2x-6
解得y=-2
(2)解:将y=
代入y=2x-6.
解得x=3.75,
再将x=3.75代入到
8x-12=30-12
解得原式=18
22.
(1)解:∵直线
经过点B(a,2),∴
.
解得
.
∵直线
经过点A(
,
)和点B(
,
),
∴
解得
∴直线
的解析式为
.
(2)解:当
时,
,解得
.
∴点C的坐标为(
,
).
设平移后的直线的解析式为
.
∵平移后的直线经过点C(
,
),
∴
.
解得
.
(3)
23.
(1)解:设直线AB的解析式为y=kx+b,
直线AB与y轴交于点B(0,﹣2),且图象过点(2,2),
把A、B两点坐标代入得
,
解得
,
直线AB的关系式;y=2x-2
(2)解:y=2x-2与x轴交点A,
y=0,
2x-2=0,
x=1,
A(1,0)
(3)解:OA=1,OB=2,
S△AOB=
=1
(4)解:OA=1,OB=2,在Rt△AOB中,由勾股定理得AB=
,
C△AOB=OA+OB+AB=3+
24.
(1)100;10
(2)∵乙车速度为80km/h,
∴甲车到达绥芬河的时间为:
,
甲车改变速度后,到达绥芬河前,设所求函数解析式为:y=kx+b(k≠0),
将(5,500)和(
,800)代入得:
,
解得
,
∴y=80x+100,
答:甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式为y=80x+100(
);
(3)100;2
解:(1)甲车改变速度前的速度为:500÷5=100(km/h),乙车达绥芬河是时间为:800÷80=10(h),
故答案为:100;10;(3)甲车到达绥芬河时,乙车距绥芬河的路程为:800﹣80×
=100(km),
40÷(100﹣80)=2(h),
即出发2h时,甲、乙两车第一次相距40km
.
故答案为:100;2.
25.
(1)120;5;(20,1200)
(2)解:①当0≤t<15时y2=120t,
②当15≤t<20时y2=1800,
③当20≤t≤35时,设此段函数解析式为y2=kx+b,
将(20,1800),(35,0),代入得
,
解得
,
∴此段的解析式为y2=-120x+4200,
综上:
;
其函数图象如图,
?
;
(3)解:由题意知,小华速度为60米/分钟,妈妈速度为120米/分钟,
①相遇前,依题意有
,解得
(分钟);
②相遇后,依题意有
,解得
(分钟);
③依题意,当
分钟时,妈妈从家里出发开始追赶小华,
此时小华距商店为
(米),只需10分钟,
即
分钟时,小华到达商店,
而此时妈妈距离商店为
(米)
(米),
∴
,解得
(分钟),
∴当t为8,12或32(分钟)时,两人相距360米.
解:(1)由题意可得:小华步行的速度为:
=60(米/分钟),
妈妈骑车的速度为:
=120(米/分钟);
妈妈回家用的时间为:
=15(分钟),
∵小华到达商店比妈妈返回商店早5分钟,
∴可知妈妈在35分钟时返回商店,
∴装货时间为:35-15×2=5(分钟),
即妈妈在家装载货物的时间为5分钟;
由题意和图像可得妈妈在M点时开始返回商店,
∴M点的横坐标为:15+5=20(分钟),
此时纵坐标为:20×60=1200(米),
∴点M的坐标为
;
故答案为:120,5,
;
一次函数单元培优测试卷
一、选择题(共10题;共30分)
1.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是(???
)
A.?数100和n,t都是常量??
B.?数100和N都是变量???????
C.?n和t都是变量???????
D.?数100和t都是变量
2.均匀地向一个容器注水,最后将容器注满,在注水的过程中,水的高度h随时间t的变化如图所示,这个容器的形状可能是(??
)
A.???B.??????C.?????D.?
3.下列图象能表示y是x的函数的是(???
)
A.?B.??C.??D.?
4.在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度
y(cm)与所挂物体的质量
x(kg)之间有如下表关系:
下列说法错误的是(???
)
A.?y
随
x
的增大而增大???B.?所挂物体质量每增加
1kg弹簧长度增加
0.5cm
C.?所挂物体为
7kg时,弹簧长度为
13.5cm?D.?不挂重物时弹簧的长度为
0cm
5.点
在函数
的图像上,则代数式
的值等于(??
)
A.?5???B.?3?????C.?-3????D.?-1
6.已知一次函数
和
的图象都经过A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是(??
)
A.?2?????B.?3???????C.?4?????D.?5
7.平面直角坐标系中,过点(-2,3)的直线
经过一、二、三象限,若点(0,a),(-1,b),(c,-1)都在直线
上,则下列判断正确的是(??
)
A.??????B.????C.??????D.?
8.在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是(???
)
A.???B.?????C.?????D.?
且
9.甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同的路线行驶,乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇,在此过程中,两车的距离y(km)与乙车行驶的时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度为120km/h;②m=160;③H点的坐标为(7,80);④n=7.4,其中正确的说法个数为(??
)
A.?1??????B.?2?????C.?3??????D.?4
10.如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是(??
)
A.?8000cm3???B.?10000
cm3???C.?2000πcm3????D.?3000πcm3
二、填空题(共8题;共24分)
11.已知一次函数y=2x-a与y=3x+b的图象交于x轴上原点外的一点,则
=________.
12.已知一次函数
,函数值
随自变量
的值增大而减小,那么
的取值范围是________.
13.小红在练习仰卧起坐,本月
日至
日的成绩与日期具有如下关系:?
日期
(日)
1
2
3
4
成绩
(个)
小红的仰卧起坐成绩y与日期
之间近似为一次函数关系,则该函数表达式为________.
14.若一次函数
的图象经过点
,则
________.
15.如图,一次图数
与一次函数
图象交于点
,则关于x的不等式组
解集为________.
16.如图,函数y=ax+b和y=kx的图象交于一点,则二元一次方程组
的解是________.
17.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为________.
18.如图,平面直角坐标系中,
,
为
轴正半轴上一点,连接
,在第一象限作
,
,过点
作直线
轴于
,直线
与直线
交于点
,且
,则直线
解析式为________.
三、解答题(共7题;共46分)
19.如下图,一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1>
y2
,
?
请直接写出x的取值范围.
20.我市人民医院准备从医疗器械销售公司采购A、B两种医疗器械共80件,其中A种器械不少于40件,B种医疗器械的数量不少于A种器械的
,
已知A种器械的售价为每件360元,B种器械的售价为每件400元。
(1)请写出人民医院在这次采购中所需资金y(元)与采购A种医疗器械x(件)的函数解析式,并写出自交量x的取位范围;
(2)为了积极应对本次新冠肺炎疫情,人民医院拿出27000元经费用于采购这80件医疗器械,请问经费是否够用,如果不够)至少还需要经费多少元?
21.已知函数y=2x-6.
(1)当x=2时,求y的值;
(2)当y=
时,求8x-12的值。
22.如图,在平面直角坐标系xOy中,一次函数
的图象经过点A(-2,4),且与正比例函数
的图象交于点B(a,2).
?
(1)求a的值及一次函数
的解析式;
(2)若一次函数
的图象与x轴交于点C,且正比例函数
的图象向下平移m(m>0)个单
位长度后经过点C,求m的值;
(3)直接写出关于x的不等式
的解集.
23.直线AB与y轴交于点B(0,﹣2),且图象过点(2,2).
(1)求直线AB的关系式;
(2)求直线AB与x轴的交点A的坐标;
(3)求△ABO的面积;
(4)求△ABO的周长.
24.团结奋战,众志成城,齐齐哈尔市组织援助医疗队,分别乘甲、乙两车同时出发,沿同一路线赶往绥芬河.齐齐哈尔距绥芬河的路程为800km
,
在行驶过程中乙车速度始终保持80km/h
,
甲车先以一定速度行驶了500km
,
用时5h
,
然后再以乙车的速度行驶,直至到达绥芬河(加油、休息时间忽略不计).甲、乙两车离齐齐哈尔的路程y(km)与所用时间x(h)的关系如图所示,请结合图象解答下列问题:
(1)甲车改变速度前的速度是________km/h
,
乙车行驶________h到达绥芬河;
(2)求甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式,不用写出自变量x的取值范围;
(3)甲车到达绥芬河时,乙车距绥芬河的路程还有________km;出发________h时,甲、乙两车第一次相距40km
.
25.小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段
表示小华和商店的距离
(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(1)填空:妈妈骑车的速度是________米/分钟,妈妈在家装载货物所用时间是________分钟,点M的坐标是________;
(2)直接写出妈妈和商店的距离
(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;
(3)求t为何值时,两人相距360米.
答案
一、选择题
1.解:数100是常量,t,n是变量,故ABD不符合题意,C符合题意.
故答案为:C.
2.解:注水量一定,函数图象的走势是稍陡,平,陡;那么高度就相应的变化,跟所给容器的粗细有关.则相应的排列顺序就为B.
故答案为:B.
3.A.如图,
,对于该x的值,有两个y值与之对应,不是函数图象;
B.如图,
,对于该x的值,有两个y值与之对应,不是函数图象;
C.如图,
对于该x的值,有两个y值与之对应,不是函数图象;
D.对每一个x的值,都有唯一确定的y值与之对应,是函数图象.
故答案为:D.
4.解:由表格可得,弹簧的长度
y(cm)与所挂物体的质量
x(kg)之间的函数关系式为:
A.
,故y随x的增大而增大,故本选项不符合题意;
B.当
时,
;当
时,
,此时
,故本选项不符合题意;
C.当
时,
,故本选项不符合题意;
D.当
时,
,故本选项符合题意.
故答案为:D
5.把
代入函数解析式
得:
,
化简得到:
,
∴
.
故答案为:C.
6.∵一次函数
和
的图象都经过A(-2,0),
∴
,
∴
,
∴两函数表达式分别为
和
,
∴直线
与直线
与
轴的交点分别为B(0,3),C(0,-1),
∴S△ABC
BC?AO
×
×2=4.
故答案为:C.
7.解法1:根据直线l经过第一、二、三象限且过点(-2,3),所以y随x的增大而增大.因为
,所以
,所以A、B、C均错;又因点(c,-1)在直线l上,所以c<-2.
解法2:过点(-2,3)作出草图,再将点(0,a),(-1,b),(c,-1)描出,即可.
故答案为:D.
8.∵
,
∴当y=0时,x=
;当x=0时,y=2t+2,
∴直线
与x轴的交点坐标为(
,0),与y轴的交点坐标为(0,2t+2),
∵t>0,
∴2t+2>2,
当t=
时,2t+2=3,此时
=-6,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图1,
当t=2时,2t+2=6,此时
=-3,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,如图2,
当t=1时,2t+2=4,
=-4,由图象知:直线
(
)与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,如图3,
∴
且
,
故答案为:D.
9.解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,
∴乙的速度为120km/h.①正确;
∵第2?6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,
∴此时甲乙距离4×40=160km,
∴m=160,②正确;
∵当乙在B休息1h时,甲前进80km,
∴H点坐标为(7,80),③正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,
∴n=6+1+0.4=7.4,④正确;
正确结论的序号为:①②③④.
故答案为:D.
10.解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
∴正方体的棱长为10cm;
∴正方体的体积为:103=1000cm3
设注水的速度为xcm3/s,圆柱的底面积为scm2
,
根据题意得:
解得:
∴圆柱形水槽的容积为:400×20=8000
cm3.
故答案为:A.
二、填空题
11.解:在一次函数y=2x?a中,令y=0,得到x=
,
在一次函数y=3x+b中,令y=0,得到x=?
,
由题意得:
=?
,图象交于x轴上原点外一点,则a≠0,且b≠0,
可以设
=?
=k,则a=2k,b=?3k,
代入
=?2.
故答案为?2.
12.解:∵函数值y随自变量x的值增大而减小,
∴1-2m<0,
∴m>.
故答案为:m>.
13.解:设y=kx+b,
根据题意得
,
解得
,
∴y与x的函数表达式为y=3x+37.
故答案为:
y=3x+37.
14.解:将(3,m)代入y=2x+2中,得2×3+2=m,
解得m=8.
故答案为:8.
15.解:当
时,
,解得
,则一次函数
与x轴的交点坐标为
,
一次图数
与一次函数
图象交于点
,
关于x的不等式组
的解集为
.
故答案为
.
16.解:由图知,函数y=ax+b和y=kx的图象交于点(2,2),
∴二元一次方程组
的解是
,
故答案为:
.
17.∵直线y=2x+4与y轴交于B点,
∴x=0时,
得y=4,
∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴C在线段OB的垂直平分线上,
∴C点纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,
解得x=﹣1.
所以C′的坐标为(﹣1,2).
18.解:过
作
轴,交
轴于
,交
于
,则
,
,
,
,
,
,
,
,
在
和
中,
,
,
,
,
,
设
,
,
,
点
在直线
上,
,
则
,
,即
,
.
点
在直线
上,
,
,
,
,
,
设直线
的解析式是
,
把
代入得:
,
即直线
的解析式是
,
故答案为:
.
三、解答题
19.
(1)解:∵
一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1)
∴-4+m=1,2k=1
解之:m=5,;
(2)
解:(2)∵一次函数y1=
-2x+m与正比例函数y2=kx的图象交于点A(2,1)
当x<2时,直线y1=
-2x+5m高于直线
y2=x
,即y1>
y2.
20.
(1)解:由题意得:y=360x+400(80-x)=-40x+32000.
∵A种器械不少于40件,B种医疗器械的数量不少于A种器械的,
∴
解之:40≤x≤50
∴x的取值范围是40≤x≤50.
(2)解:∵x的取值范围是40≤x≤50
当x=40时,y=30400
当x=50时,y=30000
∴y的取值范围是:30000≤y≤30400.
所以经费不够用,至少还需要30000-27000=3000元.
答:经费不够用,至少还需要3000元.
21.
(1)解:将x=2,代入y=2x-6
解得y=-2
(2)解:将y=
代入y=2x-6.
解得x=3.75,
再将x=3.75代入到
8x-12=30-12
解得原式=18
22.
(1)解:∵直线
经过点B(a,2),∴
.
解得
.
∵直线
经过点A(
,
)和点B(
,
),
∴
解得
∴直线
的解析式为
.
(2)解:当
时,
,解得
.
∴点C的坐标为(
,
).
设平移后的直线的解析式为
.
∵平移后的直线经过点C(
,
),
∴
.
解得
.
(3)
23.
(1)解:设直线AB的解析式为y=kx+b,
直线AB与y轴交于点B(0,﹣2),且图象过点(2,2),
把A、B两点坐标代入得
,
解得
,
直线AB的关系式;y=2x-2
(2)解:y=2x-2与x轴交点A,
y=0,
2x-2=0,
x=1,
A(1,0)
(3)解:OA=1,OB=2,
S△AOB=
=1
(4)解:OA=1,OB=2,在Rt△AOB中,由勾股定理得AB=
,
C△AOB=OA+OB+AB=3+
24.
(1)100;10
(2)∵乙车速度为80km/h,
∴甲车到达绥芬河的时间为:
,
甲车改变速度后,到达绥芬河前,设所求函数解析式为:y=kx+b(k≠0),
将(5,500)和(
,800)代入得:
,
解得
,
∴y=80x+100,
答:甲车改变速度后离齐齐哈尔的路程y(km)与所用时间x(h)之间的函数解析式为y=80x+100(
);
(3)100;2
解:(1)甲车改变速度前的速度为:500÷5=100(km/h),乙车达绥芬河是时间为:800÷80=10(h),
故答案为:100;10;(3)甲车到达绥芬河时,乙车距绥芬河的路程为:800﹣80×
=100(km),
40÷(100﹣80)=2(h),
即出发2h时,甲、乙两车第一次相距40km
.
故答案为:100;2.
25.
(1)120;5;(20,1200)
(2)解:①当0≤t<15时y2=120t,
②当15≤t<20时y2=1800,
③当20≤t≤35时,设此段函数解析式为y2=kx+b,
将(20,1800),(35,0),代入得
,
解得
,
∴此段的解析式为y2=-120x+4200,
综上:
;
其函数图象如图,
?
;
(3)解:由题意知,小华速度为60米/分钟,妈妈速度为120米/分钟,
①相遇前,依题意有
,解得
(分钟);
②相遇后,依题意有
,解得
(分钟);
③依题意,当
分钟时,妈妈从家里出发开始追赶小华,
此时小华距商店为
(米),只需10分钟,
即
分钟时,小华到达商店,
而此时妈妈距离商店为
(米)
(米),
∴
,解得
(分钟),
∴当t为8,12或32(分钟)时,两人相距360米.
解:(1)由题意可得:小华步行的速度为:
=60(米/分钟),
妈妈骑车的速度为:
=120(米/分钟);
妈妈回家用的时间为:
=15(分钟),
∵小华到达商店比妈妈返回商店早5分钟,
∴可知妈妈在35分钟时返回商店,
∴装货时间为:35-15×2=5(分钟),
即妈妈在家装载货物的时间为5分钟;
由题意和图像可得妈妈在M点时开始返回商店,
∴M点的横坐标为:15+5=20(分钟),
此时纵坐标为:20×60=1200(米),
∴点M的坐标为
;
故答案为:120,5,
;
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
