浙教版八年级上册 数学 课件: 3.4 一元一次不等式组(16张)
文档属性
| 名称 | 浙教版八年级上册 数学 课件: 3.4 一元一次不等式组(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 11:05:59 | ||
图片预览





文档简介
(共16张PPT)
3.4
一元一次不等式组
走进生活
请判断这个足球训练场的尺寸是否符合国际足球比赛的要求?(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间).
定义:
一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
走进生活
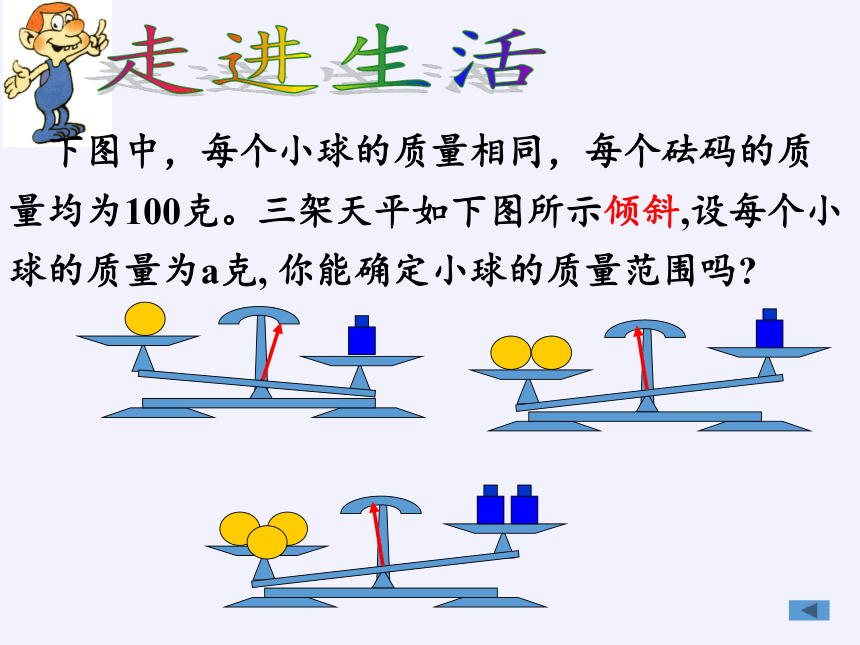
下图中,每个小球的质量相同,每个砝码的质量均为100克。三架天平如下图所示倾斜,设每个小球的质量为a克,
你能确定小球的质量范围吗?
下列式子中,哪些是一元一次不等式组?
不是
不是
√
√
√
√
(5)2-x<x≤6-2x
辨一辨
100
101
102
103
104
105
106
107
108
109
110
100
101
102
103
104
105
106
107
108
109
110
组成不等式组的各个不等式的解的公共部分就是不等式组的解。
探究
100
101
102
103
104
105
106
107
108
109
110
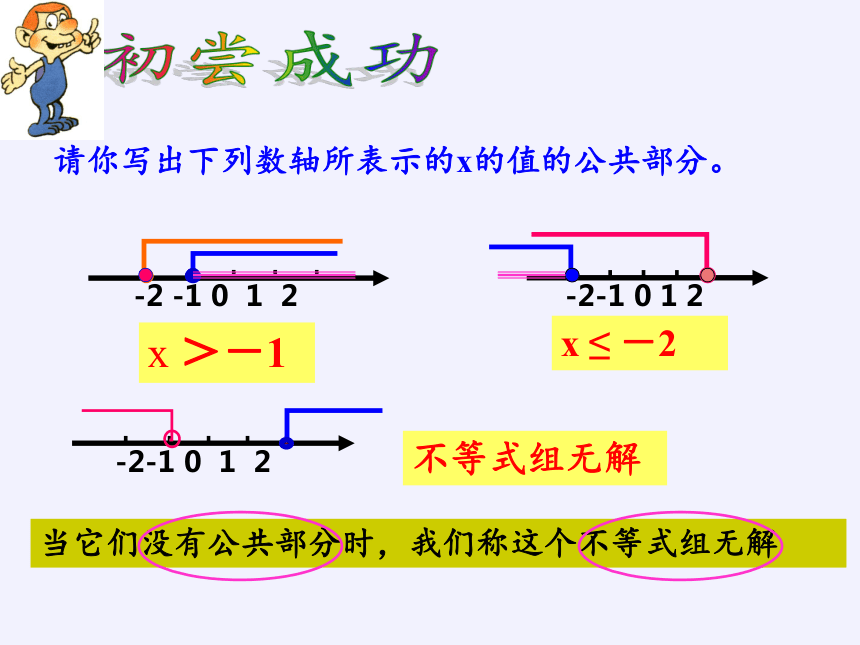
请你写出下列数轴所表示的x的值的公共部分。
-2
-1
0
1
2
x
>-1
-2-1
0
1
2
x
≤
-2
-2-1
0
1
2
初尝成功
当它们没有公共部分时,我们称这个不等式组无解
不等式组无解
利用数轴,求出满足下列各组不等式的x
值的公共部分
独立挑战
(1)
???????????????????(2)
?
?
(3)
?????????????
(4)
??????
思考一:你能从中感悟出不等式组的解有什么规律吗?
不等式组的解的口诀
1.
大大取大
2.小小取小
3.大小小大中间找
4.大大小小则无解
典例教学
思考二:请归纳出解一元一次不等式组的步骤吗?
解一元一次不等式组的步骤
1.
求分解
2.画公解
3.写组解(注意边界点)
例1:解一元一次不等式组
①
②
解下列一元一次不等式组:
我巩固我提升
(1)
(2)
挑战极限
已知关于x的不等式组
的整数解
共有6个,则a
的取值范围为
体会与分享
你学到了什么?
你还有什么困惑吗?
你有什么经验与收获与大家一起共享吗?
小结
作业布置
必做题:《作业本》3.4
选做题:《优化与提高》
P90—10,12,13,14
逆向训练
3
-2
1、
若不等式组
x-b<0
的解为
2<
x<3
,则a=
;
b=
x+a>0
逆向训练
D
2、若不等式组
x>a
的解为
x
>
b
,则下列各式正确的是(
)
x
>
b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
变式(一)若不等式组
x>a
的解为
x
≥
b
,则下列各式正确的是(
)
x
≥
b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
变式(二)若不等式组
x>-
a
的解为
x
≥
-b
,则下列各式正确的是(
)
x
≥
-b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
B
A
谢
谢
3.4
一元一次不等式组
走进生活
请判断这个足球训练场的尺寸是否符合国际足球比赛的要求?(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间).
定义:
一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
走进生活
下图中,每个小球的质量相同,每个砝码的质量均为100克。三架天平如下图所示倾斜,设每个小球的质量为a克,
你能确定小球的质量范围吗?
下列式子中,哪些是一元一次不等式组?
不是
不是
√
√
√
√
(5)2-x<x≤6-2x
辨一辨
100
101
102
103
104
105
106
107
108
109
110
100
101
102
103
104
105
106
107
108
109
110
组成不等式组的各个不等式的解的公共部分就是不等式组的解。
探究
100
101
102
103
104
105
106
107
108
109
110
请你写出下列数轴所表示的x的值的公共部分。
-2
-1
0
1
2
x
>-1
-2-1
0
1
2
x
≤
-2
-2-1
0
1
2
初尝成功
当它们没有公共部分时,我们称这个不等式组无解
不等式组无解
利用数轴,求出满足下列各组不等式的x
值的公共部分
独立挑战
(1)
???????????????????(2)
?
?
(3)
?????????????
(4)
??????
思考一:你能从中感悟出不等式组的解有什么规律吗?
不等式组的解的口诀
1.
大大取大
2.小小取小
3.大小小大中间找
4.大大小小则无解
典例教学
思考二:请归纳出解一元一次不等式组的步骤吗?
解一元一次不等式组的步骤
1.
求分解
2.画公解
3.写组解(注意边界点)
例1:解一元一次不等式组
①
②
解下列一元一次不等式组:
我巩固我提升
(1)
(2)
挑战极限
已知关于x的不等式组
的整数解
共有6个,则a
的取值范围为
体会与分享
你学到了什么?
你还有什么困惑吗?
你有什么经验与收获与大家一起共享吗?
小结
作业布置
必做题:《作业本》3.4
选做题:《优化与提高》
P90—10,12,13,14
逆向训练
3
-2
1、
若不等式组
x-b<0
的解为
2<
x<3
,则a=
;
b=
x+a>0
逆向训练
D
2、若不等式组
x>a
的解为
x
>
b
,则下列各式正确的是(
)
x
>
b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
变式(一)若不等式组
x>a
的解为
x
≥
b
,则下列各式正确的是(
)
x
≥
b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
变式(二)若不等式组
x>-
a
的解为
x
≥
-b
,则下列各式正确的是(
)
x
≥
-b
A.
a>b
B.
a<b
C.
b
≤a
D.
a
≤
b
B
A
谢
谢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
