浙教版初中数学九年级上册 第四章相似三角形复习——--相似的基本图形:K型课件(15张)
文档属性
| 名称 | 浙教版初中数学九年级上册 第四章相似三角形复习——--相似的基本图形:K型课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 240.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 19:51:56 | ||
图片预览


文档简介
(共15张PPT)
----相似的基本图形:K型
相似三角形复习
A
C
B
D
A
D
E
B
C
A
D
E
B
C
A
B
C
D
E
∠ACB=Rt∠
CD⊥AB
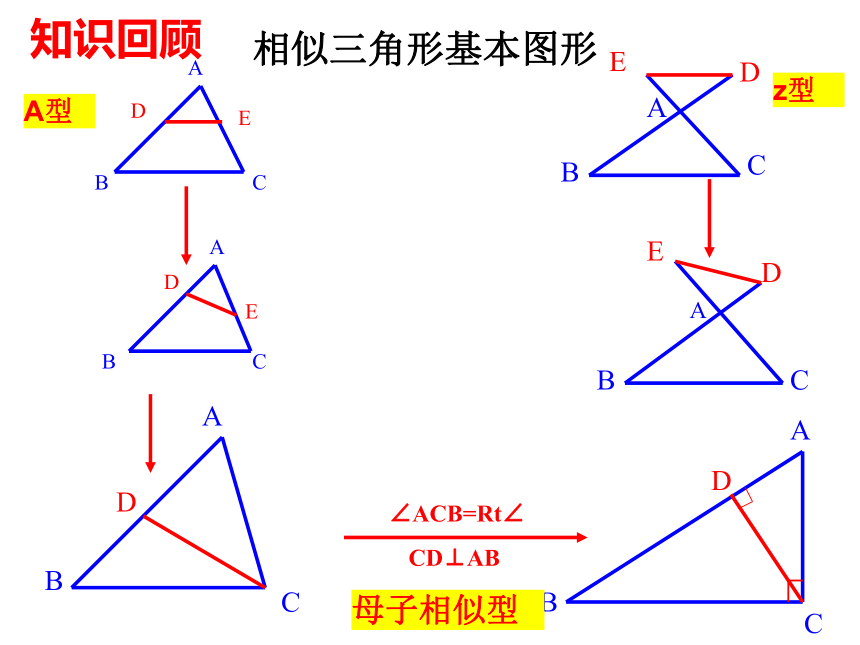
相似三角形基本图形
A
B
C
D
A型
z型
B
C
A
D
E
母子相似型
知识回顾
从A形图
z形图到……
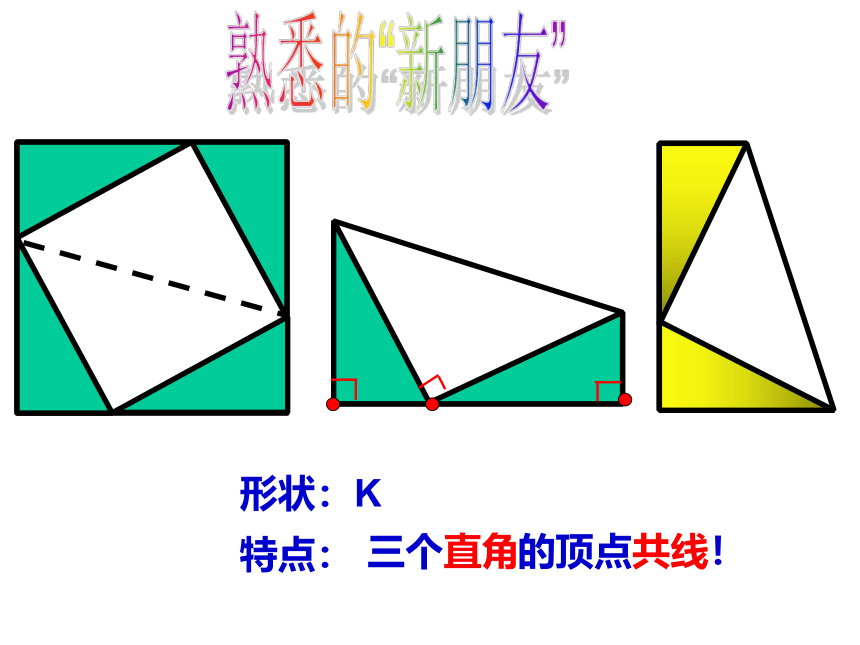
熟悉的“新朋友”
特点:
形状:K
三个直角
的顶点共线!
A
B
C
P
D
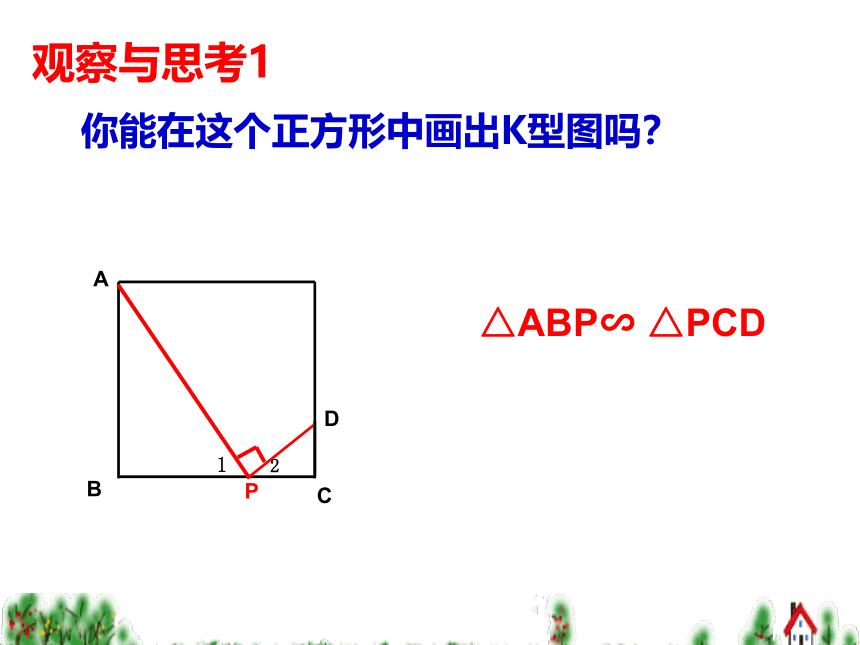
△ABP∽
△PCD
观察与思考1
你能在这个正方形中画出K型图吗?
1
2
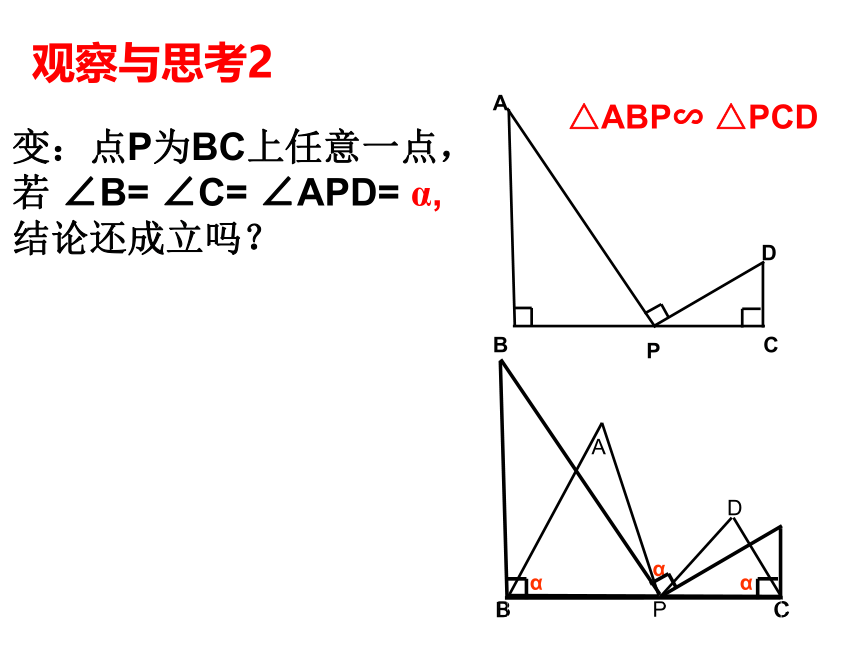
变:点P为BC上任意一点,若
∠B=
∠C=
∠APD=
α,
结论还成立吗?
C
α
α
α
A
B
P
D
B
C
C
A
B
P
D
△ABP∽
△PCD
观察与思考2
△ABP∽
△PCD
A
B
C
D
P
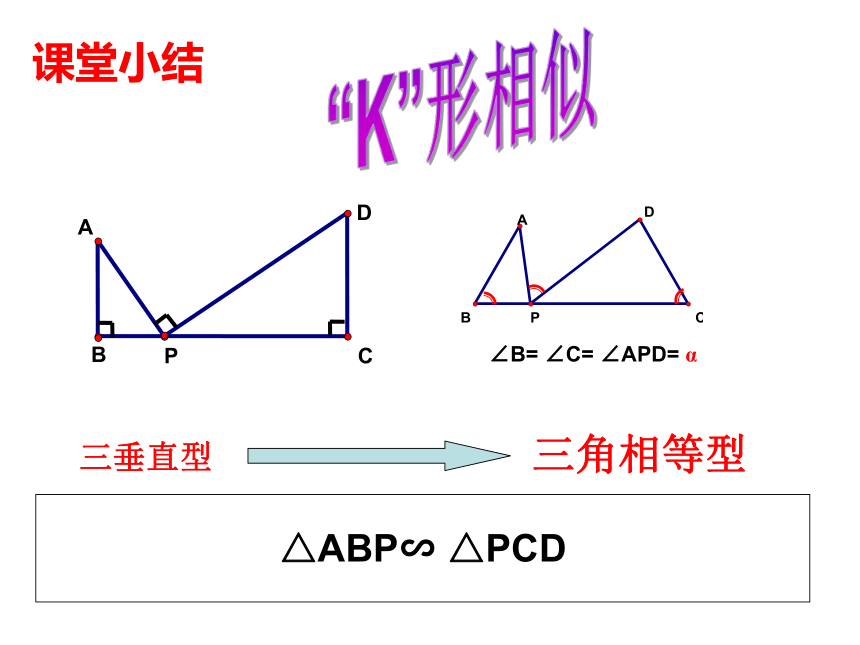
三角相等型
三垂直型
课堂小结
“K”形相似
∠B=
∠C=
∠APD=
α
1、如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
1
三角相等型
题组应用
如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
)2
1
证明:∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
又∵∠ADE=45°
∴∠ADE=∠B
∴∠1=∠2
∴
△ABD∽△DCE
如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
解:
∵△ABD∽△DCE
1
∴
∴
∴
当
时
2.如图,由8个大小相等的小正方形构成的图案,它的四个顶点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上。
A
B
C
D
E
G
H
F
若AB=4,BC=6,求DG的长.
(1)求点B的坐标;
y
x
o
A(1,2)
B
C
D
3.如图,已知点A(1,2)是函数
的图象
的点,连接OA,作OA⊥OB,与图象
交于点B.
(2)求OA︰OB的值;
(1)求点B的坐标;
y
x
o
B
C
D
3.如图,已知点A(1,2)是函数
的图象
的点,连接OA,作OA⊥OB,与图象
交于点B.
(2)求OA︰OB的值;
(3)若点A在双曲线上移
动,
保持OA⊥OB
不变,OA︰OB的值变吗?
A
如图,已知抛物线与x轴交于A、B
两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足
∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴
上是否存在点E,使得以A、O、E
为顶点的三角形与⊿PBC相似?若
存在,求出点E的坐标;若不存在,
请说明理由.
A
B
P
C
O
x
y
X=4
2
3
Q
6
拓展提高
△ABP∽
△PCD
A
B
C
D
P
三角相等型
三垂直型
课堂反思
“K”形相似
∠B=
∠C=
∠APD=
α
----相似的基本图形:K型
相似三角形复习
A
C
B
D
A
D
E
B
C
A
D
E
B
C
A
B
C
D
E
∠ACB=Rt∠
CD⊥AB
相似三角形基本图形
A
B
C
D
A型
z型
B
C
A
D
E
母子相似型
知识回顾
从A形图
z形图到……
熟悉的“新朋友”
特点:
形状:K
三个直角
的顶点共线!
A
B
C
P
D
△ABP∽
△PCD
观察与思考1
你能在这个正方形中画出K型图吗?
1
2
变:点P为BC上任意一点,若
∠B=
∠C=
∠APD=
α,
结论还成立吗?
C
α
α
α
A
B
P
D
B
C
C
A
B
P
D
△ABP∽
△PCD
观察与思考2
△ABP∽
△PCD
A
B
C
D
P
三角相等型
三垂直型
课堂小结
“K”形相似
∠B=
∠C=
∠APD=
α
1、如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
1
三角相等型
题组应用
如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
)2
1
证明:∵AB=AC,∠BAC=90°
∴∠B=∠C=45°
又∵∠ADE=45°
∴∠ADE=∠B
∴∠1=∠2
∴
△ABD∽△DCE
如图,在等腰△ABC中,
∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°
A
B
C
D
E
(1)求证:△ABD∽△DCE
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值
解:
∵△ABD∽△DCE
1
∴
∴
∴
当
时
2.如图,由8个大小相等的小正方形构成的图案,它的四个顶点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上。
A
B
C
D
E
G
H
F
若AB=4,BC=6,求DG的长.
(1)求点B的坐标;
y
x
o
A(1,2)
B
C
D
3.如图,已知点A(1,2)是函数
的图象
的点,连接OA,作OA⊥OB,与图象
交于点B.
(2)求OA︰OB的值;
(1)求点B的坐标;
y
x
o
B
C
D
3.如图,已知点A(1,2)是函数
的图象
的点,连接OA,作OA⊥OB,与图象
交于点B.
(2)求OA︰OB的值;
(3)若点A在双曲线上移
动,
保持OA⊥OB
不变,OA︰OB的值变吗?
A
如图,已知抛物线与x轴交于A、B
两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)抛物线上有一点P,满足
∠PBC=90°,求点P的坐标;
(3)在(2)的条件下,问在y轴
上是否存在点E,使得以A、O、E
为顶点的三角形与⊿PBC相似?若
存在,求出点E的坐标;若不存在,
请说明理由.
A
B
P
C
O
x
y
X=4
2
3
Q
6
拓展提高
△ABP∽
△PCD
A
B
C
D
P
三角相等型
三垂直型
课堂反思
“K”形相似
∠B=
∠C=
∠APD=
α
同课章节目录
