浙教版初中数学九年级上册 4.4 两个相似三角形 的判定 课件(15张)
文档属性
| 名称 | 浙教版初中数学九年级上册 4.4 两个相似三角形 的判定 课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览

文档简介
(共15张PPT)
4.4
两个三角形相似的判定(一)
知识回顾
A
Cˊ
Bˊ
A
ˊ
C
B
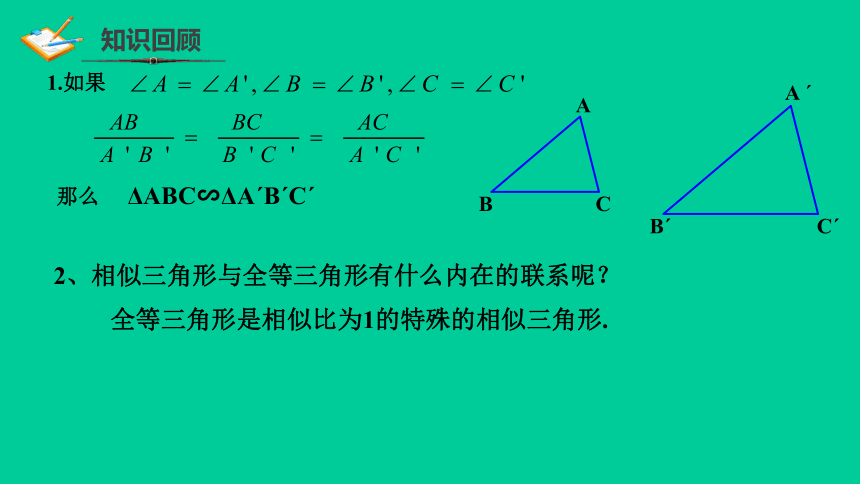
1.如果
那么
ΔABC∽ΔAˊBˊCˊ
2、相似三角形与全等三角形有什么内在的联系呢?
全等三角形是相似比为1的特殊的相似三角形.
探索新知
A
B
C
D
E
A
B
C
D
E
F
G
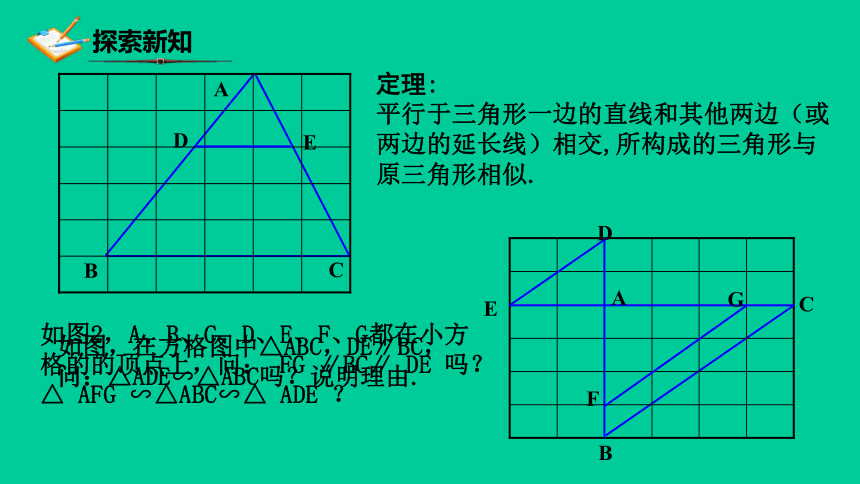
如图,在方格图中△ABC,DE∥BC,问:△ADE∽△ABC吗?说明理由.
如图2,A、B、C、D、E、F、G都在小方格的的顶点上,问:
FG
∥BC∥
DE
吗?
△
AFG
∽△ABC∽△
ADE
?
定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
练一练
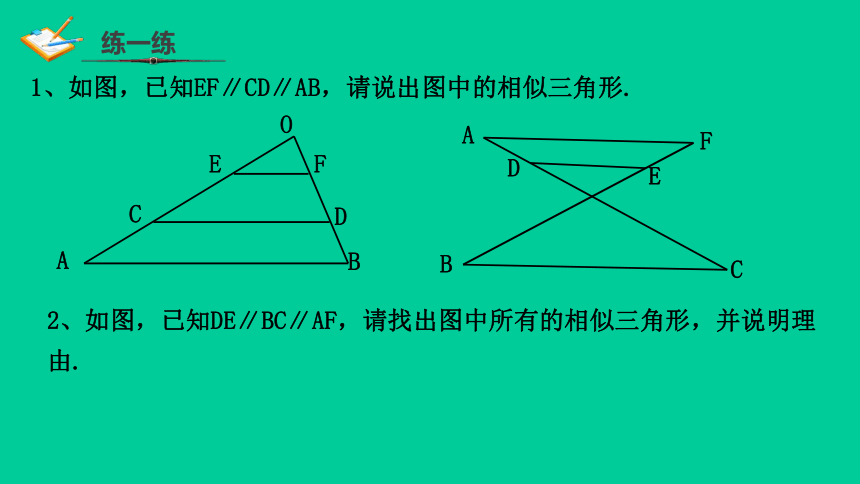
1、如图,已知EF∥CD∥AB,请说出图中的相似三角形.
2、如图,已知DE∥BC∥AF,请找出图中所有的相似三角形,并说明理由.
A
B
F
C
D
E
O
A
B
C
D
E
F
探索新知
A
B
C
Aˊ
Cˊ
Bˊ
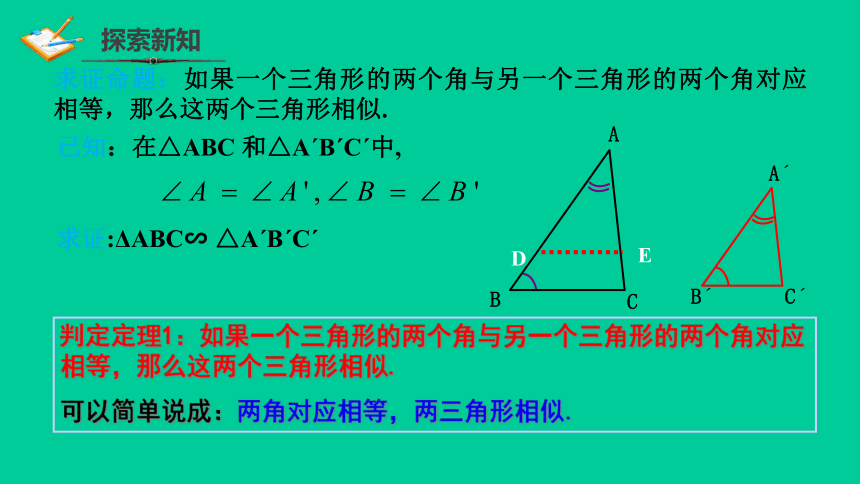
求证命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
已知:在△ABC
和△AˊBˊCˊ中,
求证:ΔABC∽
△AˊBˊCˊ
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:两角对应相等,两三角形相似.
D
E
例题讲解
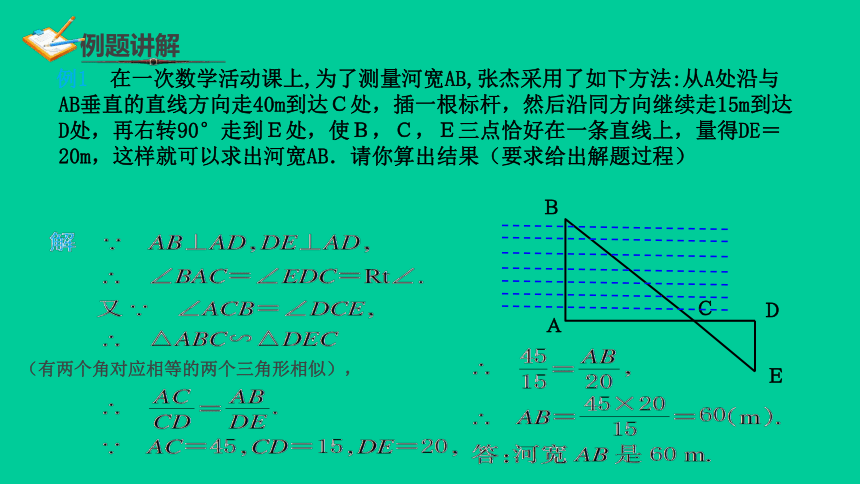
例1
在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
B
A
C
D
E
(有两个角对应相等的两个三角形相似),
例题讲解
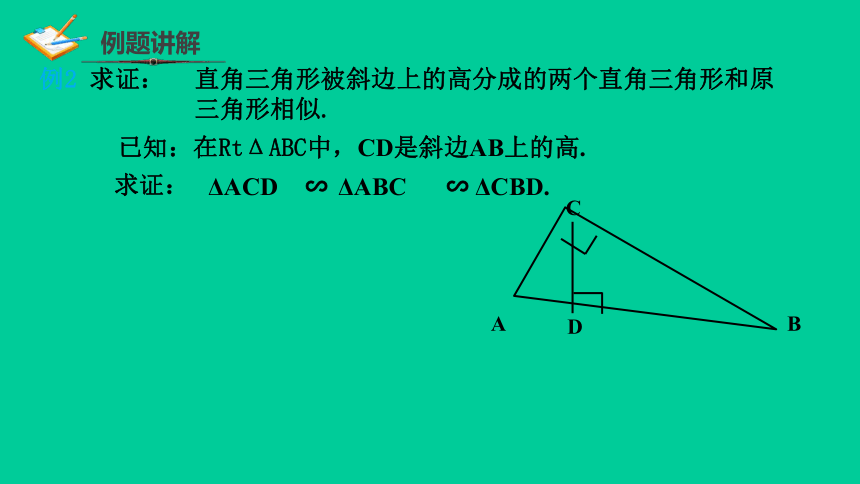
直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
A
D
B
C
已知:在RtΔABC中,CD是斜边AB上的高.
求证:
ΔABC
ΔACD
∽
ΔCBD.
∽
例2
求证:
例3
已知:ΔABC和ΔDEF中,∠A=40°,∠B=80°,
∠E=80°,∠F=60
°求证:ΔABC∽ΔDEF.
A
F
E
C
B
D
40°
80°
80°
60°
练一练
(1)已知ΔABC与ΔA′B′C′中,∠B=∠B
′
=750,∠C=500,∠A′=550,这两个三角形相似吗?为什么?
A
B
C
A′
B′
C′
750
750
500
550
550
练一练
(2)已知等腰三角形ΔABC和ΔA′B′
C′中,∠A、∠A′分别是顶角,
求证:①若∠A=∠A′,则ΔABC∽ΔA′B′C′.
②若∠B=∠B′,则ΔABC∽ΔA′B′C′.
A
B
C
A′
B′
C′
A
B
C
A
′
B′
C′
1.已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F.
(2)图中还有与ΔAEF相似的三角形吗?请一一写出.
A
B
C
D
E
(1)求证:ΔAEF∽ΔADC;
F
拓展提高
D
2.如图,在ΔABC中
,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与ΔABC相似?
A
B
C
D
E
A
B
C
D
E
拓展提高
拓展提高
3.过Rt△ABC的斜边AB上一点D作一条直线与另一边AC或者BC相交,使截得的小三角形与△ABC相似,这样的直线有几条?
C
●
A
B
D
拓展提高
A
C
B
D
E
4.如图,△ABC内接于圆O,∠BAC的平分线分别交圆O
,BC于点D,E,连结BD,CD.
(2)根据题中条件,找出图中各对相似三角形.
(1)求证:△ABE∽△CDE.
小结
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
2.相似三角形的判定定理1:两角对应相等,两三角形相似.
4.相似三角形判定定理的应用.
4.4
两个三角形相似的判定(一)
知识回顾
A
Cˊ
Bˊ
A
ˊ
C
B
1.如果
那么
ΔABC∽ΔAˊBˊCˊ
2、相似三角形与全等三角形有什么内在的联系呢?
全等三角形是相似比为1的特殊的相似三角形.
探索新知
A
B
C
D
E
A
B
C
D
E
F
G
如图,在方格图中△ABC,DE∥BC,问:△ADE∽△ABC吗?说明理由.
如图2,A、B、C、D、E、F、G都在小方格的的顶点上,问:
FG
∥BC∥
DE
吗?
△
AFG
∽△ABC∽△
ADE
?
定理:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
练一练
1、如图,已知EF∥CD∥AB,请说出图中的相似三角形.
2、如图,已知DE∥BC∥AF,请找出图中所有的相似三角形,并说明理由.
A
B
F
C
D
E
O
A
B
C
D
E
F
探索新知
A
B
C
Aˊ
Cˊ
Bˊ
求证命题:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
已知:在△ABC
和△AˊBˊCˊ中,
求证:ΔABC∽
△AˊBˊCˊ
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:两角对应相等,两三角形相似.
D
E
例题讲解
例1
在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40m到达C处,插一根标杆,然后沿同方向继续走15m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,量得DE=20m,这样就可以求出河宽AB.请你算出结果(要求给出解题过程)
B
A
C
D
E
(有两个角对应相等的两个三角形相似),
例题讲解
直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
A
D
B
C
已知:在RtΔABC中,CD是斜边AB上的高.
求证:
ΔABC
ΔACD
∽
ΔCBD.
∽
例2
求证:
例3
已知:ΔABC和ΔDEF中,∠A=40°,∠B=80°,
∠E=80°,∠F=60
°求证:ΔABC∽ΔDEF.
A
F
E
C
B
D
40°
80°
80°
60°
练一练
(1)已知ΔABC与ΔA′B′C′中,∠B=∠B
′
=750,∠C=500,∠A′=550,这两个三角形相似吗?为什么?
A
B
C
A′
B′
C′
750
750
500
550
550
练一练
(2)已知等腰三角形ΔABC和ΔA′B′
C′中,∠A、∠A′分别是顶角,
求证:①若∠A=∠A′,则ΔABC∽ΔA′B′C′.
②若∠B=∠B′,则ΔABC∽ΔA′B′C′.
A
B
C
A′
B′
C′
A
B
C
A
′
B′
C′
1.已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F.
(2)图中还有与ΔAEF相似的三角形吗?请一一写出.
A
B
C
D
E
(1)求证:ΔAEF∽ΔADC;
F
拓展提高
D
2.如图,在ΔABC中
,点D、E分别是边AB、AC上的点,连结DE,利用所学的知识讨论:当具备怎样的条件时,ΔADE与ΔABC相似?
A
B
C
D
E
A
B
C
D
E
拓展提高
拓展提高
3.过Rt△ABC的斜边AB上一点D作一条直线与另一边AC或者BC相交,使截得的小三角形与△ABC相似,这样的直线有几条?
C
●
A
B
D
拓展提高
A
C
B
D
E
4.如图,△ABC内接于圆O,∠BAC的平分线分别交圆O
,BC于点D,E,连结BD,CD.
(2)根据题中条件,找出图中各对相似三角形.
(1)求证:△ABE∽△CDE.
小结
1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3.定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
2.相似三角形的判定定理1:两角对应相等,两三角形相似.
4.相似三角形判定定理的应用.
同课章节目录
