浙教版初中数学九年级上册第四章 相似三角形 的动点问题作业讲评 课件(20张)
文档属性
| 名称 | 浙教版初中数学九年级上册第四章 相似三角形 的动点问题作业讲评 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 273.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 10:43:17 | ||
图片预览



文档简介
(共20张PPT)
相似三角形的动点问题
——优化作业讲评
情景引入
如图,△ABC中,∠C>∠B,点D在边AC上.
1.如何在边AB上作一点E,
使△ADE与△ABC相似,
请说明理由.
2.过点D作直线截△ABC,使截得的三角形与原三角形相似,那么这样的直线有几条?
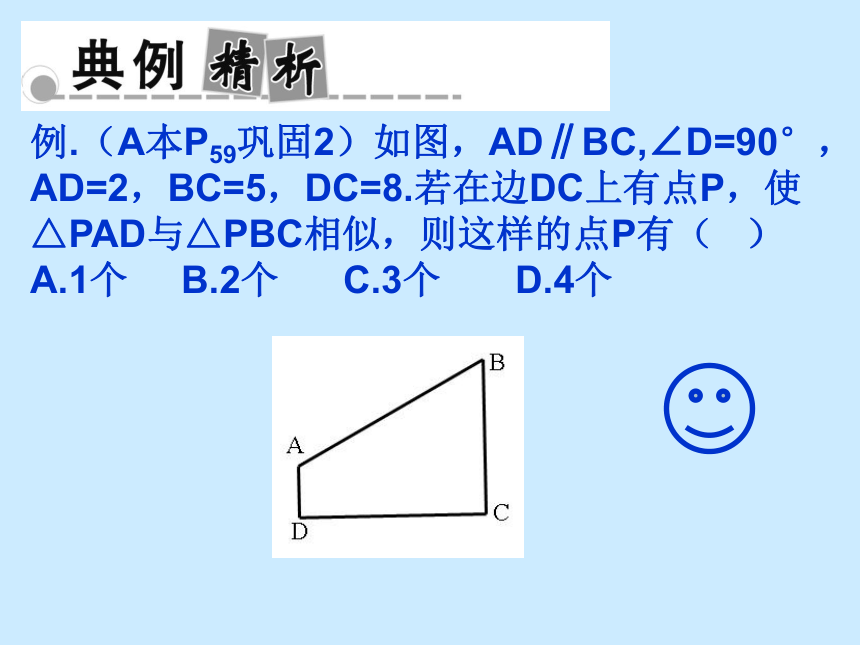
例.(A本P59巩固2)如图,AD∥BC,∠D=90°,
AD=2,BC=5,DC=8.若在边DC上有点P,使
△PAD与△PBC相似,则这样的点P有(
)
A.1个
B.2个
C.3个
D.4个
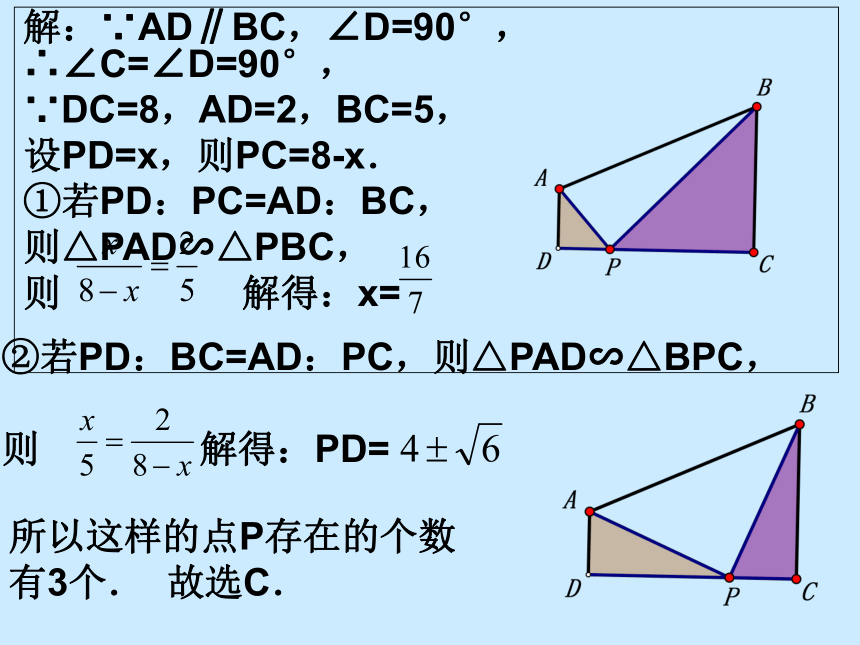
解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,
∵DC=8,AD=2,BC=5,
设PD=x,则PC=8-x.
①若PD:PC=AD:BC,
则△PAD∽△PBC,
则
解得:x=
②若PD:BC=AD:PC,则△PAD∽△BPC,
则
解得:PD=
所以这样的点P存在的个数有3个.
故选C.
1
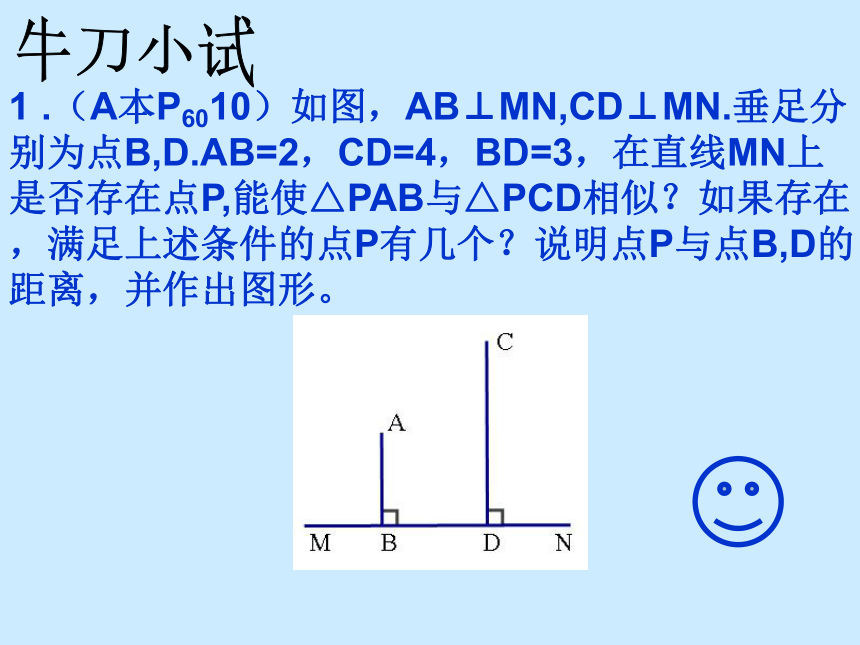
.(A本P6010)如图,AB⊥MN,CD⊥MN.垂足分
别为点B,D.AB=2,CD=4,BD=3,在直线MN上
是否存在点P,能使△PAB与△PCD相似?如果存在
,满足上述条件的点P有几个?说明点P与点B,D的
距离,并作出图形。
牛刀小试
解
:存在4个点.
(1).当P在B左侧时
设PB=x,则PD=x+3
因为三角形PAB相似三角形PCD
则
PB/PD=AB/CD
或AB/PD=PB/CD
解得
PB=3
,PD=6;PB=
,PD=
(2).当P在线段BD上
设PB=x,则PD=3-x
同上
解得
PB=1
,PD=2;
(3).当P在D右侧时
设PB=x,则PD=x-3
同上
解得
PB=
,PD=
所以共4个点
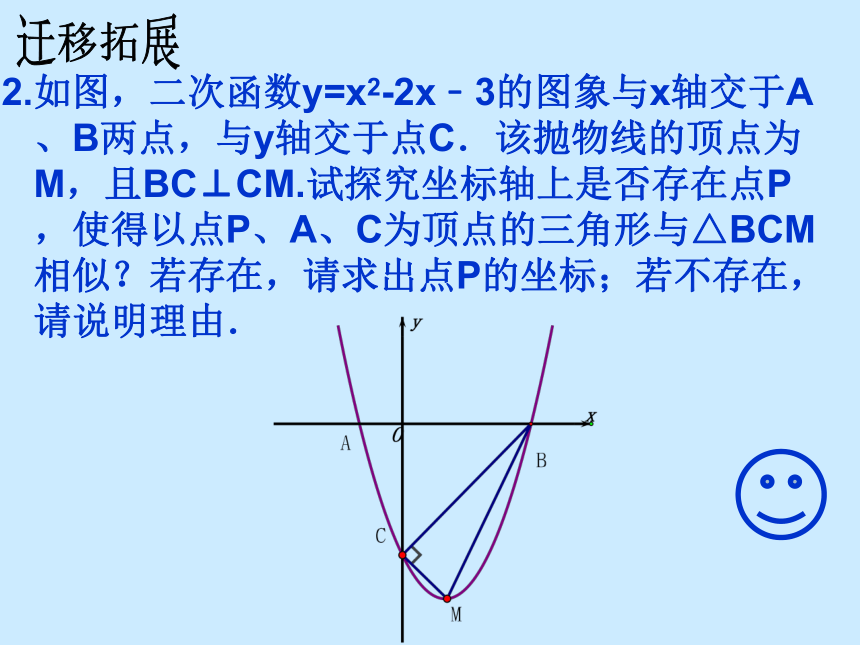
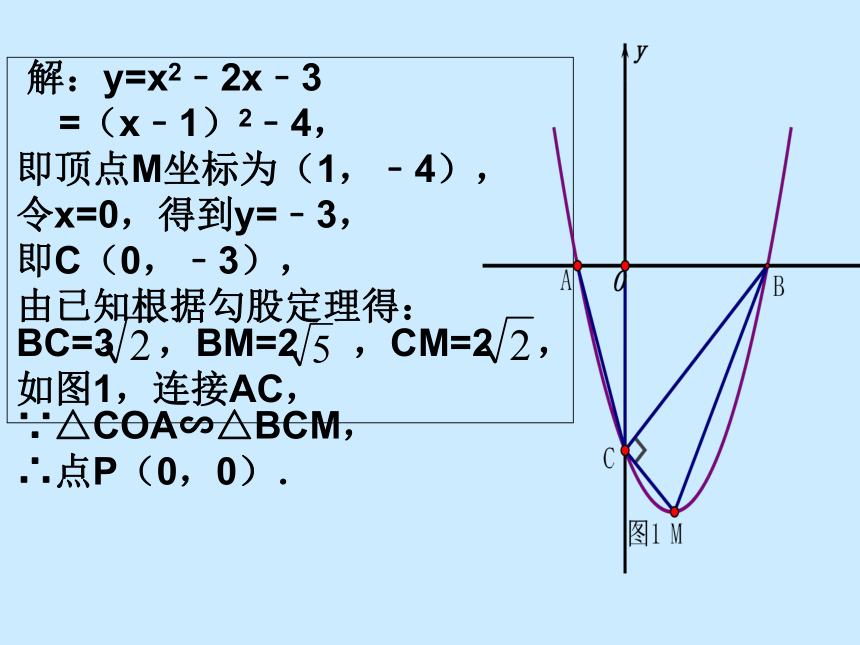
2.如图,二次函数y=x2-2x﹣3的图象与x轴交于A、B两点,与y轴交于点C.该抛物线的顶点为M,且BC⊥CM.试探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标;若不存在,请说明理由.
迁移拓展
解:y=x2﹣2x﹣3
=(x﹣1)2﹣4,
即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,
即C(0,﹣3),
由已知根据勾股定理得:BC=3
,BM=2
,CM=2
,
如图1,连接AC,∵△COA∽△BCM,
∴点P(0,0).
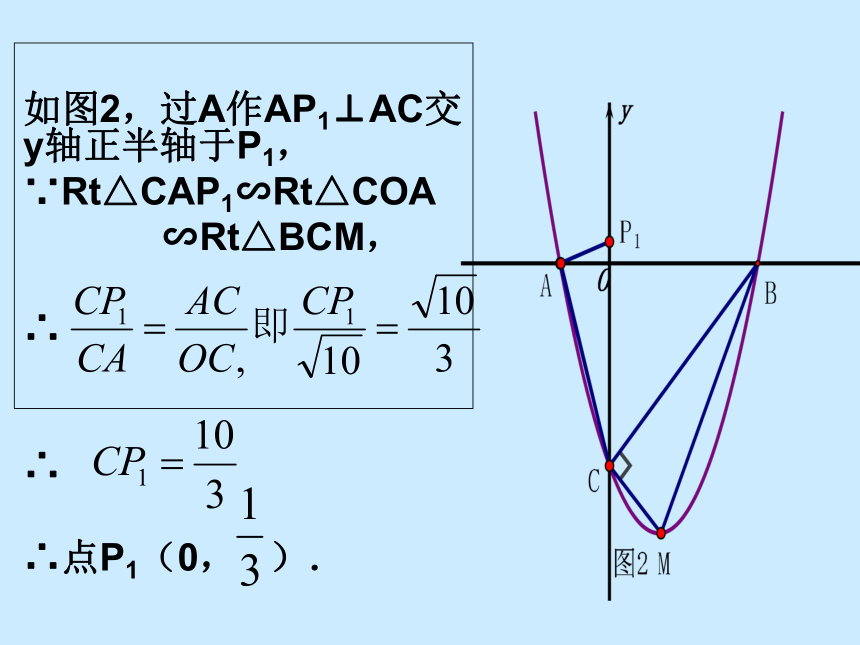
如图2,过A作AP1⊥AC交y轴正半轴于P1,
∵Rt△CAP1∽Rt△COA
∽Rt△BCM,
∴
∴
∴点P1(0,
).
如图3,过C作CP2⊥AC交x轴正半轴于P2,
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴
∴AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,
)
P2(9,0).
说说你在这节课中的收获与体会
2、思想方法:分类讨论;数形结合等
......
收获和体会
1、解题步骤:?合理分类;
?画出示意图;
?列方程求解.
1.(B本P80典例4)如图,△ABC内接于
⊙O,
且∠ABC=∠C,点D在BC上运动.过点D作DE∥
BC,DE交AB的延长线于点E,连接BD.
(1)求证:AD2=AC?AE.
(2)当点D运动到什么位置时,△DBE∽△ADE?
请利用图2进行探索和证明。
大展身手
证明:(1)在△ABC中,∵∠C=∠ADB,
∠ABC=∠C
∴∠ADB=∠ABC,
∵DE∥BC,∴∠ABC=∠E,∴∠ADB=∠E;
又因为∠BAD为公共角,
∴△ABD∽△ADE,
∴AB:AD=AD:AE,
即AD2=AB?AE.
(2)运动到BC的中点时△DBE∽△ADE.
此时AD为⊙O的直径,∠ABD=90°,AD⊥BC
∵DE∥BC,
∴AD⊥DE
,
∠ADE=∠DBE=90°,
因为∠E为公共角,
∴△DBE∽△ADE.
2.(B本P7013)如图,正方形ABCD的边长为4
,E是BC边的中点,点P在射线AD上,过点P作
PF⊥AE于F。
(1)求证:
△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否
存在实数x,使以P,F,E为顶点的三角形也与△ABE
相似?若存在,请求出x的值;若不存在请说明理由。
大展身手
(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,且∠ABE=90°,
∴∠PAF=∠AEB,
又∵PF⊥AE,
∴∠PFA=∠ABE=90°∴△PFA∽△ABE;
(2)①当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形,
∴PA=EB=2,即x=2.
②当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB
∴∠PEF=∠PAF,
∴PE=PA
∵PF⊥AE,
∴点F为AE的中点,
∵
∴
由
得PE=5,
即x=5
3.(B本P80巩固4)已知,在边长为1的圆内接正方
形ABCD中,P为边CD的中点,直线AP交圆于E点.
(1)求弦DE的长.
(2)若Q是线段BC上一动点,当BQ长为何值时,
△ADP与以Q,C,P为顶点的三角形相似?
大展身手
(1)如图1.过D点作DF⊥AE于F点.在Rt△ADP中,
又∵S△ADP=
AD?DP=
AP?DF
∴
∵AD=DC=BC=BA,∴AD=DC=BC=BA,
∵AD的度数为90°
∴∠DEA=45°
∴EF=DF=
∴
(2)如图2.当Rt△ADP∽Rt△QCP时有
得:QC=1.
即点Q与点B重合
∴BQ=0
如图3,当Rt△ADP∽Rt△PCQ时,有
得QC=
即BQ=BC-CQ=
∴当BQ=0或
时,三角形ADP与以点Q,C,P为顶点
的三角形相似.
解决动点问题的关键是在认真审题的基础上先做到静中求动,根据题意画一些不同运动时刻的图形,想像从头到尾的整个运动过程,对整个运动过程有一个初步的理解,理清运动过程中的各种情形;然后是做到动中取静,画出运动过程中各种情形的瞬间图形,寻找变化的本质,或将图中的相关线段代数化,转化为函数问题或方程问题解决.
相似三角形的动点问题
——优化作业讲评
情景引入
如图,△ABC中,∠C>∠B,点D在边AC上.
1.如何在边AB上作一点E,
使△ADE与△ABC相似,
请说明理由.
2.过点D作直线截△ABC,使截得的三角形与原三角形相似,那么这样的直线有几条?
例.(A本P59巩固2)如图,AD∥BC,∠D=90°,
AD=2,BC=5,DC=8.若在边DC上有点P,使
△PAD与△PBC相似,则这样的点P有(
)
A.1个
B.2个
C.3个
D.4个
解:∵AD∥BC,∠D=90°,
∴∠C=∠D=90°,
∵DC=8,AD=2,BC=5,
设PD=x,则PC=8-x.
①若PD:PC=AD:BC,
则△PAD∽△PBC,
则
解得:x=
②若PD:BC=AD:PC,则△PAD∽△BPC,
则
解得:PD=
所以这样的点P存在的个数有3个.
故选C.
1
.(A本P6010)如图,AB⊥MN,CD⊥MN.垂足分
别为点B,D.AB=2,CD=4,BD=3,在直线MN上
是否存在点P,能使△PAB与△PCD相似?如果存在
,满足上述条件的点P有几个?说明点P与点B,D的
距离,并作出图形。
牛刀小试
解
:存在4个点.
(1).当P在B左侧时
设PB=x,则PD=x+3
因为三角形PAB相似三角形PCD
则
PB/PD=AB/CD
或AB/PD=PB/CD
解得
PB=3
,PD=6;PB=
,PD=
(2).当P在线段BD上
设PB=x,则PD=3-x
同上
解得
PB=1
,PD=2;
(3).当P在D右侧时
设PB=x,则PD=x-3
同上
解得
PB=
,PD=
所以共4个点
2.如图,二次函数y=x2-2x﹣3的图象与x轴交于A、B两点,与y轴交于点C.该抛物线的顶点为M,且BC⊥CM.试探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标;若不存在,请说明理由.
迁移拓展
解:y=x2﹣2x﹣3
=(x﹣1)2﹣4,
即顶点M坐标为(1,﹣4),
令x=0,得到y=﹣3,
即C(0,﹣3),
由已知根据勾股定理得:BC=3
,BM=2
,CM=2
,
如图1,连接AC,∵△COA∽△BCM,
∴点P(0,0).
如图2,过A作AP1⊥AC交y轴正半轴于P1,
∵Rt△CAP1∽Rt△COA
∽Rt△BCM,
∴
∴
∴点P1(0,
).
如图3,过C作CP2⊥AC交x轴正半轴于P2,
∵Rt△P2CA∽Rt△COA∽Rt△BCM,
∴
∴AP2=10,
∴点P2(9,0).
∴符合条件的点有三个:O(0,0),P1(0,
)
P2(9,0).
说说你在这节课中的收获与体会
2、思想方法:分类讨论;数形结合等
......
收获和体会
1、解题步骤:?合理分类;
?画出示意图;
?列方程求解.
1.(B本P80典例4)如图,△ABC内接于
⊙O,
且∠ABC=∠C,点D在BC上运动.过点D作DE∥
BC,DE交AB的延长线于点E,连接BD.
(1)求证:AD2=AC?AE.
(2)当点D运动到什么位置时,△DBE∽△ADE?
请利用图2进行探索和证明。
大展身手
证明:(1)在△ABC中,∵∠C=∠ADB,
∠ABC=∠C
∴∠ADB=∠ABC,
∵DE∥BC,∴∠ABC=∠E,∴∠ADB=∠E;
又因为∠BAD为公共角,
∴△ABD∽△ADE,
∴AB:AD=AD:AE,
即AD2=AB?AE.
(2)运动到BC的中点时△DBE∽△ADE.
此时AD为⊙O的直径,∠ABD=90°,AD⊥BC
∵DE∥BC,
∴AD⊥DE
,
∠ADE=∠DBE=90°,
因为∠E为公共角,
∴△DBE∽△ADE.
2.(B本P7013)如图,正方形ABCD的边长为4
,E是BC边的中点,点P在射线AD上,过点P作
PF⊥AE于F。
(1)求证:
△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否
存在实数x,使以P,F,E为顶点的三角形也与△ABE
相似?若存在,请求出x的值;若不存在请说明理由。
大展身手
(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,且∠ABE=90°,
∴∠PAF=∠AEB,
又∵PF⊥AE,
∴∠PFA=∠ABE=90°∴△PFA∽△ABE;
(2)①当△EFP∽△ABE,且∠PEF=∠EAB时,
则有PE∥AB
∴四边形ABEP为矩形,
∴PA=EB=2,即x=2.
②当△PFE∽△ABE,且∠PEF=∠AEB时,
∵∠PAF=∠AEB
∴∠PEF=∠PAF,
∴PE=PA
∵PF⊥AE,
∴点F为AE的中点,
∵
∴
由
得PE=5,
即x=5
3.(B本P80巩固4)已知,在边长为1的圆内接正方
形ABCD中,P为边CD的中点,直线AP交圆于E点.
(1)求弦DE的长.
(2)若Q是线段BC上一动点,当BQ长为何值时,
△ADP与以Q,C,P为顶点的三角形相似?
大展身手
(1)如图1.过D点作DF⊥AE于F点.在Rt△ADP中,
又∵S△ADP=
AD?DP=
AP?DF
∴
∵AD=DC=BC=BA,∴AD=DC=BC=BA,
∵AD的度数为90°
∴∠DEA=45°
∴EF=DF=
∴
(2)如图2.当Rt△ADP∽Rt△QCP时有
得:QC=1.
即点Q与点B重合
∴BQ=0
如图3,当Rt△ADP∽Rt△PCQ时,有
得QC=
即BQ=BC-CQ=
∴当BQ=0或
时,三角形ADP与以点Q,C,P为顶点
的三角形相似.
解决动点问题的关键是在认真审题的基础上先做到静中求动,根据题意画一些不同运动时刻的图形,想像从头到尾的整个运动过程,对整个运动过程有一个初步的理解,理清运动过程中的各种情形;然后是做到动中取静,画出运动过程中各种情形的瞬间图形,寻找变化的本质,或将图中的相关线段代数化,转化为函数问题或方程问题解决.
同课章节目录
