浙教版初中数学九年级上册 3.5 圆周角 课件(17张)
文档属性
| 名称 | 浙教版初中数学九年级上册 3.5 圆周角 课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 15:40:47 | ||
图片预览

文档简介
(共17张PPT)
3.4
圆周角(1)
O
A
B
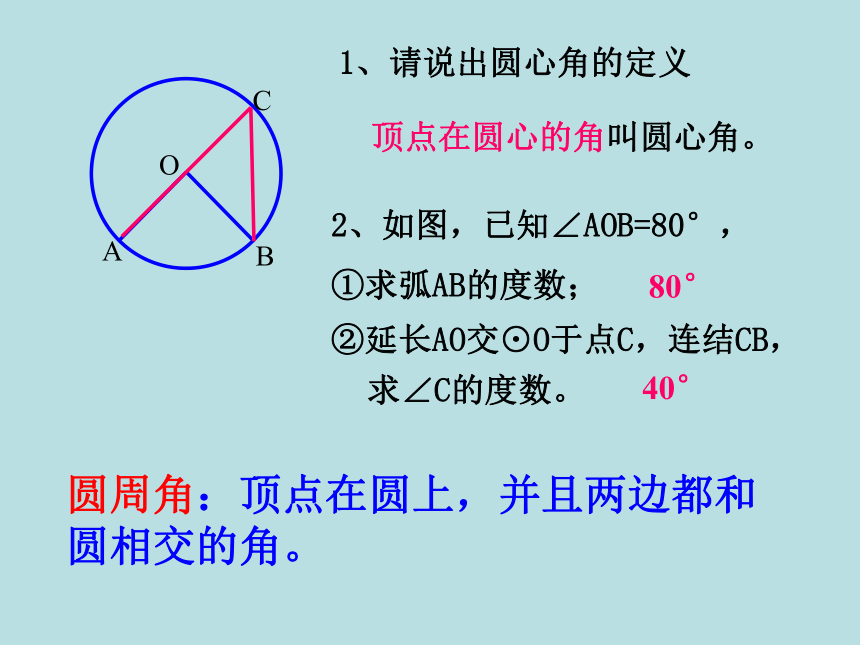
圆周角:顶点在圆上,并且两边都和圆相交的角。
1、请说出圆心角的定义
顶点在圆心的角叫圆心角。
2、如图,已知∠AOB=80°,
①求弧AB的度数;
C
80°
40°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
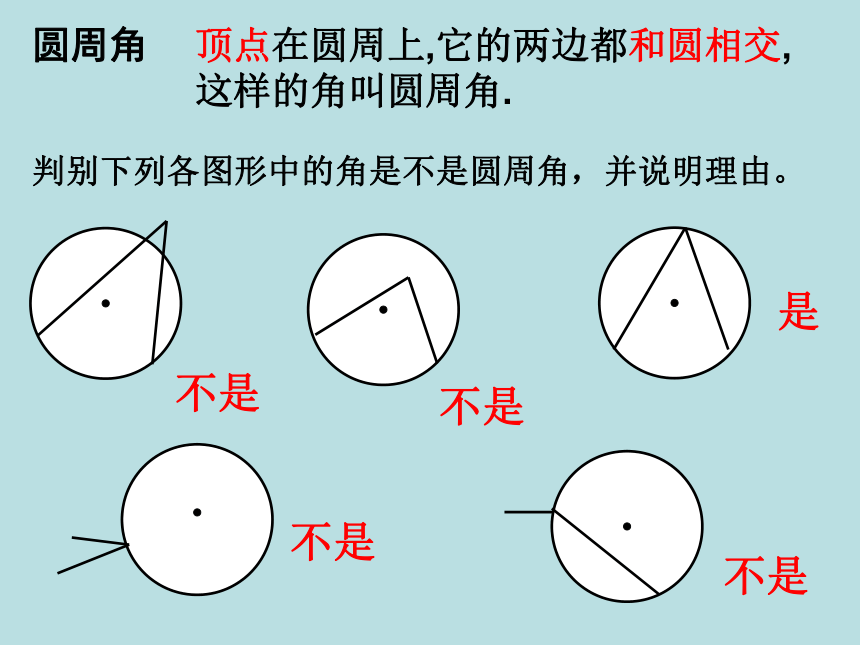
判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
圆周角
顶点在圆周上,它的两边都和圆相交,这样的角叫圆周角.
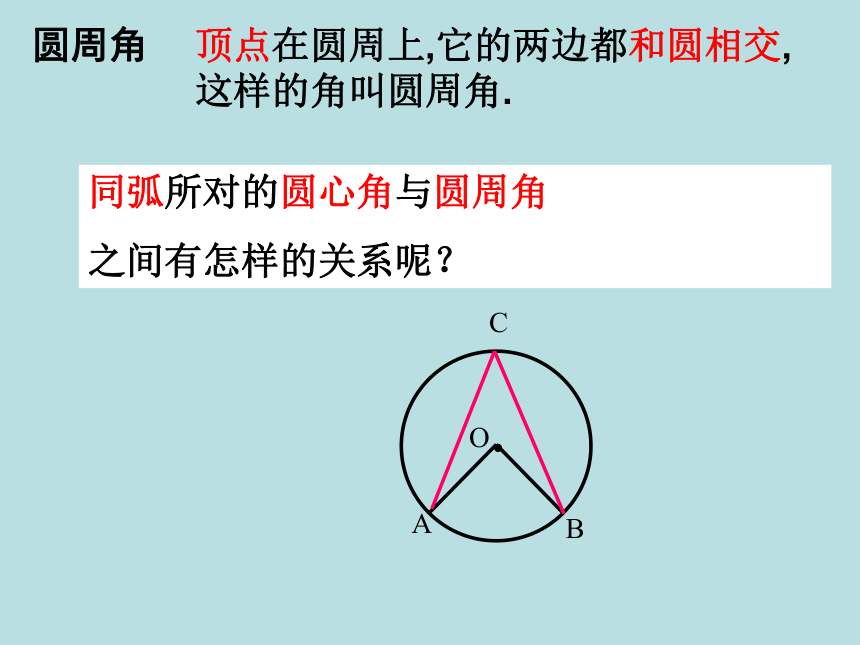
圆周角
顶点在圆周上,它的两边都和圆相交,这样的角叫圆周角.
同弧所对的圆心角与圆周角
之间有怎样的关系呢?
O
A
B
C
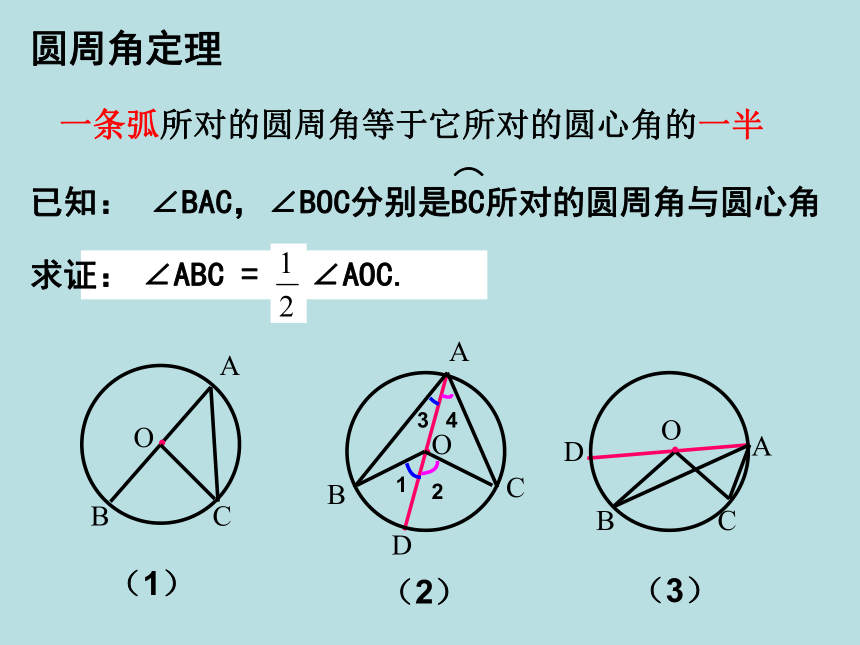
已知:
∠BAC,∠BOC分别是BC所对的圆周角与圆心角
⌒
∠ABC
=
∠AOC.
求证:
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
A
B
C
O
.
(1)
A
B
C
O
.
D
(2)
C
O
A
B
D
.
(3)
1
2
3
4
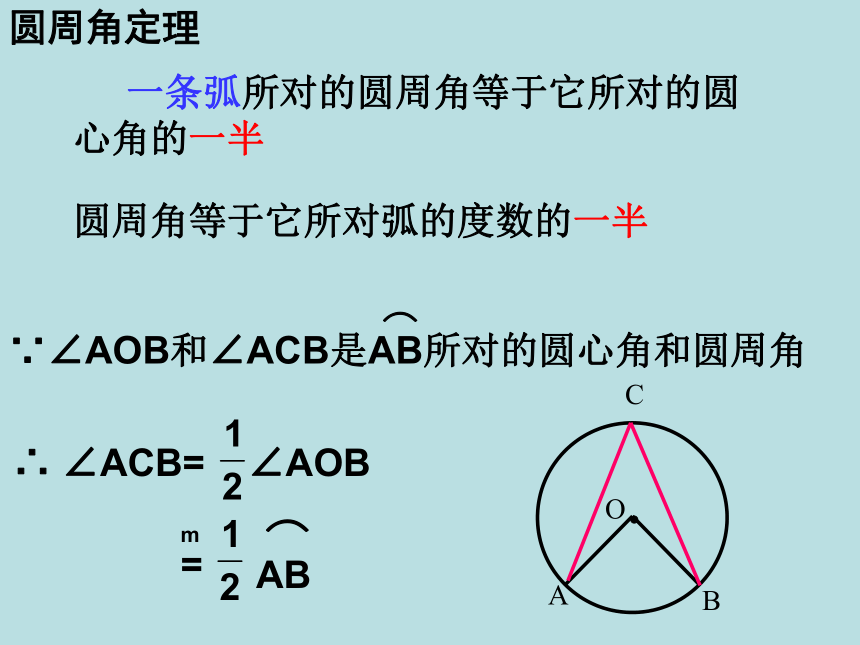
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
∵∠AOB和∠ACB是AB所对的圆心角和圆周角
⌒
∴
∠ACB=
∠AOB
圆周角等于它所对弧的度数的一半
O
A
B
C
=
⌒
AB
m
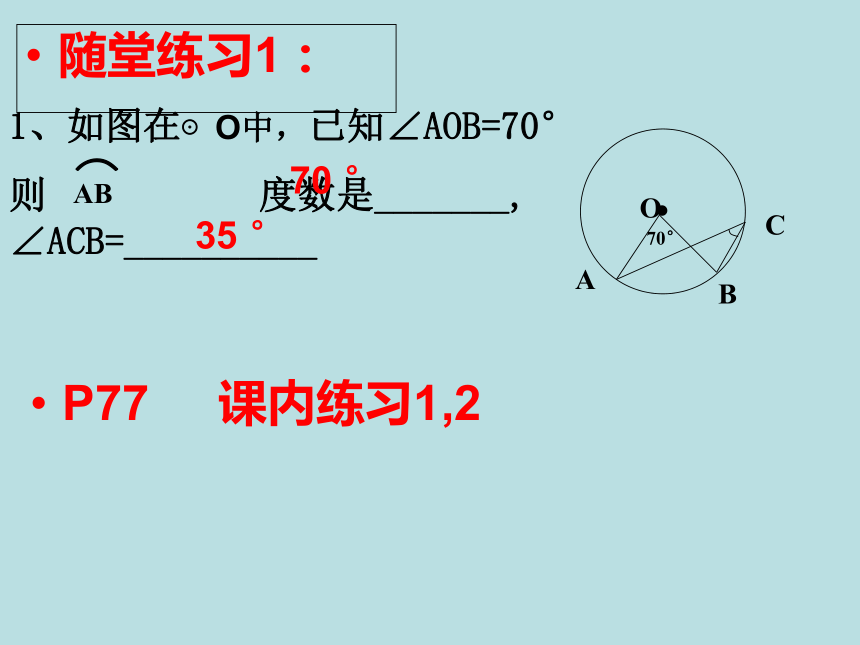
随堂练习1:
B
A
O
.
70°
C
1、如图在⊙O中,已知∠AOB=70°
则
度数是_______,
∠ACB=__________
AB
⌒
70
°
35
°
P77
课内练习1,2
2.如图,BC是⊙O的直径,A是⊙O上任一点,
求∠BAC的度数.
B
C
O
A
F
E
推论1:
90°的圆周角所对的弦是直径。
半圆(或直径)所对的圆周角是直角;
A
3.如图,圆周角∠BAC
=90?,弦BC经过圆心O吗?为什么?
●O
B
C
已知:如图,四边形ABCD的四个顶点在⊙O上.
求证:∠B+∠D=180?
例1:
A
O
B
C
D
四边形的四个顶点都在圆上,称四边形内接于圆,
这个四边形叫做圆的内接四边形
圆内接四边形对角互补
1、如图,A,B,C,D是⊙O上的四点,且∠BCD=100°,求∠BOD和∠BAD的大小
C
A
B
O.
D
随堂练习2:
100°
2.如图,AB是⊙O的直径,C是⊙O上的点,已知∠AOC=45°,则∠B=_______,
∠A=_________;
∠ACB=_______
B
A
C
O.
22.5°
62.5°
90°
3.如图,四边形ABCD内接于⊙O
,
∠A=85°,
∠D=100°,点E在AB的延长线上,求∠C,
∠CBE的度数.
O.
B
A
C
D
E
85°
100°
4.⊙O中,圆心角∠AOB=56°,则弦AB所对的圆周角等于(
)
A
B
O.
第1个回答必错
D
C
A.28
°
B.112
°
C.28
°或
152
°
D.124
°或56
°
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是
。
O
1
2
1、圆周角定义。
2、圆周角定理及其定理应用。
五、总结扩展:
①一条弧所对的圆周角等于它所对的圆心角的一半
②半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
③圆内接四边形对角互补
5.如图,⊙C经过原点,并与两坐标轴交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),求点A与圆心C的坐标
O
A
B
.
C
D
y
x
想一想:
6.如图,AB是⊙O的直径,AB=AC,
∠BAC=50°,BC交⊙O于点D,
①求证:BD=CD
②求∠BOD的度数
思考题:如图,在⊙O中,DE=2BC,
∠
EOD=64°,求∠
A的度数。
︵
︵
A
B
C
D
E
O
3.4
圆周角(1)
O
A
B
圆周角:顶点在圆上,并且两边都和圆相交的角。
1、请说出圆心角的定义
顶点在圆心的角叫圆心角。
2、如图,已知∠AOB=80°,
①求弧AB的度数;
C
80°
40°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
圆周角
顶点在圆周上,它的两边都和圆相交,这样的角叫圆周角.
圆周角
顶点在圆周上,它的两边都和圆相交,这样的角叫圆周角.
同弧所对的圆心角与圆周角
之间有怎样的关系呢?
O
A
B
C
已知:
∠BAC,∠BOC分别是BC所对的圆周角与圆心角
⌒
∠ABC
=
∠AOC.
求证:
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
A
B
C
O
.
(1)
A
B
C
O
.
D
(2)
C
O
A
B
D
.
(3)
1
2
3
4
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半
∵∠AOB和∠ACB是AB所对的圆心角和圆周角
⌒
∴
∠ACB=
∠AOB
圆周角等于它所对弧的度数的一半
O
A
B
C
=
⌒
AB
m
随堂练习1:
B
A
O
.
70°
C
1、如图在⊙O中,已知∠AOB=70°
则
度数是_______,
∠ACB=__________
AB
⌒
70
°
35
°
P77
课内练习1,2
2.如图,BC是⊙O的直径,A是⊙O上任一点,
求∠BAC的度数.
B
C
O
A
F
E
推论1:
90°的圆周角所对的弦是直径。
半圆(或直径)所对的圆周角是直角;
A
3.如图,圆周角∠BAC
=90?,弦BC经过圆心O吗?为什么?
●O
B
C
已知:如图,四边形ABCD的四个顶点在⊙O上.
求证:∠B+∠D=180?
例1:
A
O
B
C
D
四边形的四个顶点都在圆上,称四边形内接于圆,
这个四边形叫做圆的内接四边形
圆内接四边形对角互补
1、如图,A,B,C,D是⊙O上的四点,且∠BCD=100°,求∠BOD和∠BAD的大小
C
A
B
O.
D
随堂练习2:
100°
2.如图,AB是⊙O的直径,C是⊙O上的点,已知∠AOC=45°,则∠B=_______,
∠A=_________;
∠ACB=_______
B
A
C
O.
22.5°
62.5°
90°
3.如图,四边形ABCD内接于⊙O
,
∠A=85°,
∠D=100°,点E在AB的延长线上,求∠C,
∠CBE的度数.
O.
B
A
C
D
E
85°
100°
4.⊙O中,圆心角∠AOB=56°,则弦AB所对的圆周角等于(
)
A
B
O.
第1个回答必错
D
C
A.28
°
B.112
°
C.28
°或
152
°
D.124
°或56
°
半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是
。
O
1
2
1、圆周角定义。
2、圆周角定理及其定理应用。
五、总结扩展:
①一条弧所对的圆周角等于它所对的圆心角的一半
②半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。
③圆内接四边形对角互补
5.如图,⊙C经过原点,并与两坐标轴交于A,D两点,已知∠OBA=30°,点D的坐标为(0,2),求点A与圆心C的坐标
O
A
B
.
C
D
y
x
想一想:
6.如图,AB是⊙O的直径,AB=AC,
∠BAC=50°,BC交⊙O于点D,
①求证:BD=CD
②求∠BOD的度数
思考题:如图,在⊙O中,DE=2BC,
∠
EOD=64°,求∠
A的度数。
︵
︵
A
B
C
D
E
O
同课章节目录
