浙教版初中数学八年级上册5.2 函数 课件(共20张ppt)
文档属性
| 名称 | 浙教版初中数学八年级上册5.2 函数 课件(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 19:34:16 | ||
图片预览




文档简介
(共20张PPT)
认识函数
知识回顾:
在一个变化过程中,______________的量称为变量, ____________的量称为常量.
问题1、小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。常量是___________, 变量是_____________
16元/时
t时、m元
能用t的代数式表示m的值吗?
m=16t
如果t取一个确定值,那么m相应的取几个值?
对于变量t取一个确定的值,变量m相应的也取唯一确定的值.
可以取不同值
固定不变
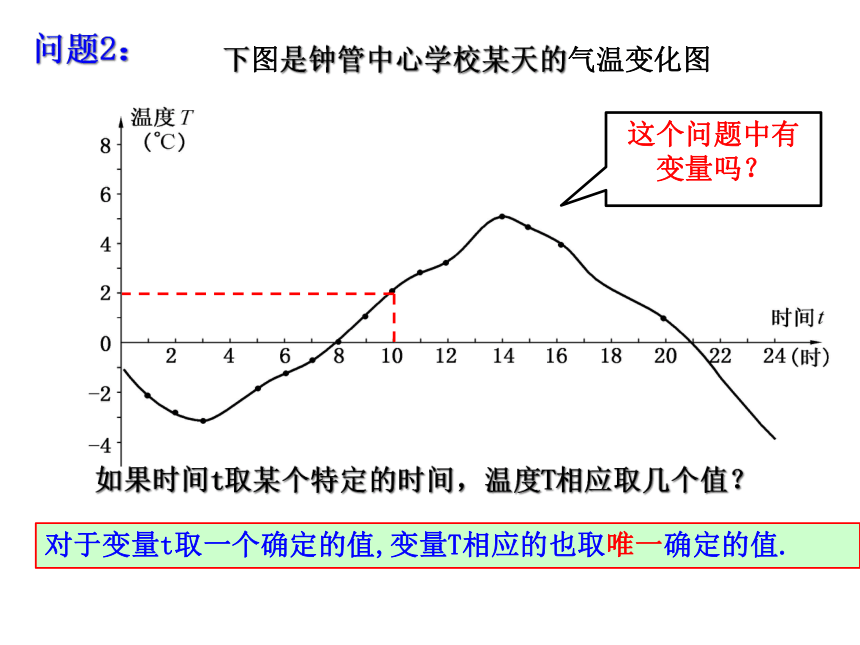
如果时间t取某个特定的时间,温度T相应取几个值?
下图是钟管中心学校某天的气温变化图
问题2:
这个问题中有变量吗?
对于变量t取一个确定的值,变量T相应的也取唯一确定的值.
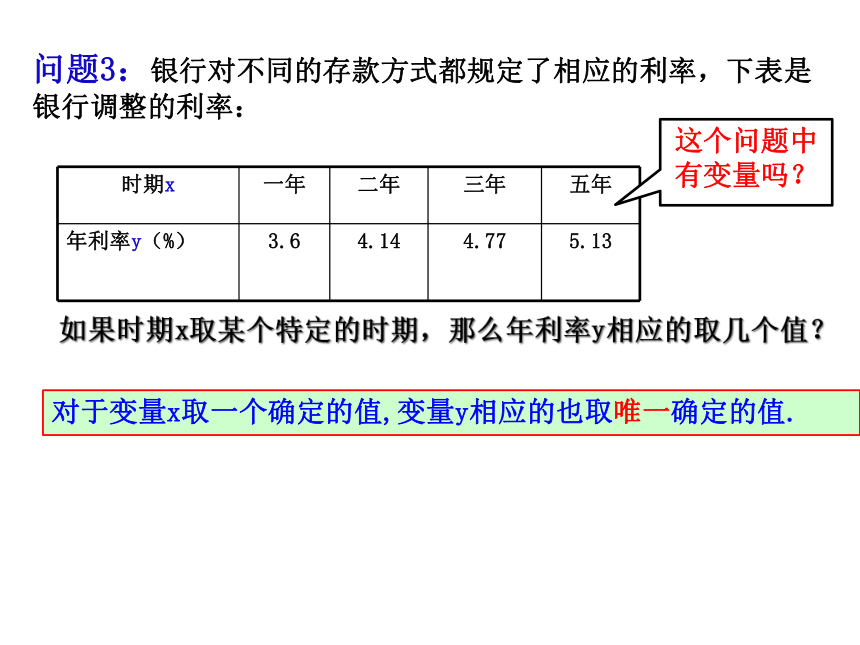
问题3:银行对不同的存款方式都规定了相应的利率,下表是银行调整的利率:
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
这个问题中有变量吗?
如果时期x取某个特定的时期,那么年利率y相应的取几个值?
对于变量x取一个确定的值,变量y相应的也取唯一确定的值.
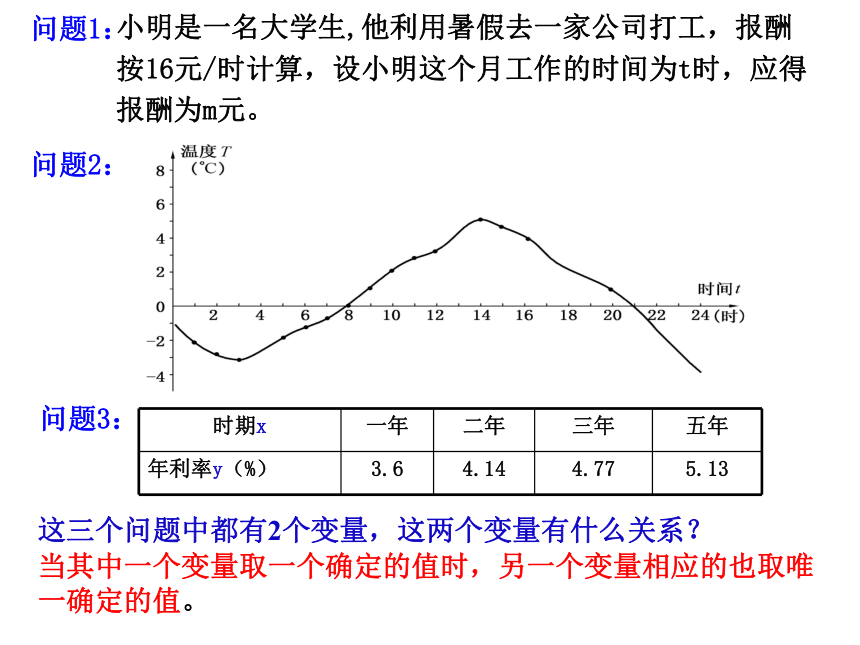
这三个问题中都有2个变量,这两个变量有什么关系?
当其中一个变量取一个确定的值时,另一个变量相应的也取唯一确定的值。
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。
问题3:
问题2:
问题1:
问题1、小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。则
m=16t
对于变量t的每一个确定的值,变量m都有唯一确定的值.
函数的概念:
一般地,在某个变化过程中,设有两个变量x和y,如果对于x的每一个确定的值,y相应的都有唯一确定的值,那我们就说y是x的函数,其中x叫做自变量。
注意:函数指的是两个变量之间的一种关系。
m是t的函数,t是自变量.
象m=16t这种表示函数关系的等式叫函数解析式,简称函数式。
m关于t的函数解析式
函数解析式的书写要求:通常等式的左边是表示函数一个字母.
,右边是含自变量的代数式。
用函数解析式表示函数的方法叫解析法。
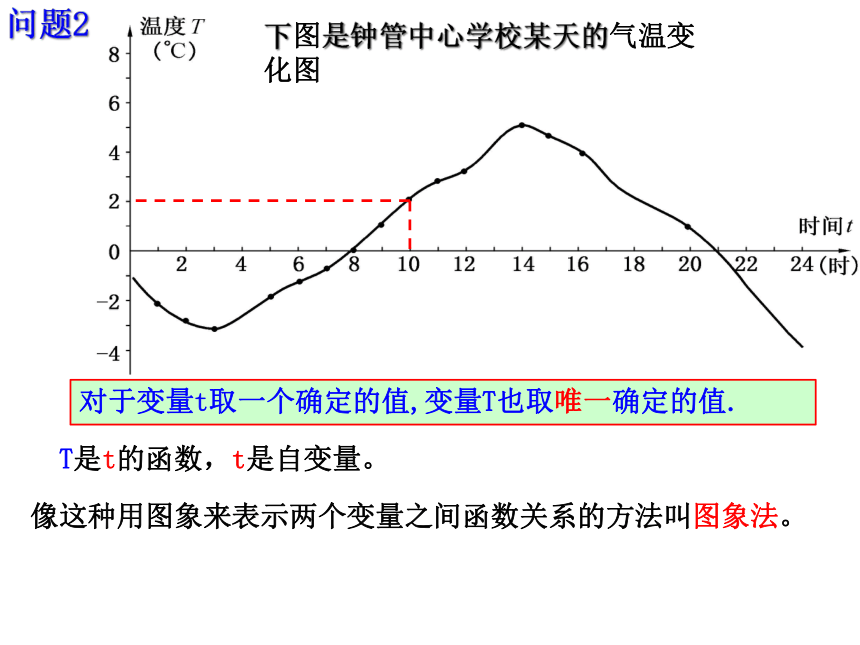
问题2:
下图是钟管中心学校某天的气温变化图
对于变量t取一个确定的值,变量T也取唯一确定的值.
T是t的函数,t是自变量。
像这种用图象来表示两个变量之间函数关系的方法叫图象法。
问题3:银行对不同的存款方式都规定了相应的利率,下表是银行调整的利率:
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
对于变量x取一个确定的值,变量y也取唯一确定的值.
y是x的函数,x是自变量。
像这种把两个变量之间函数关系列成表格的形式的方法叫
列表法。
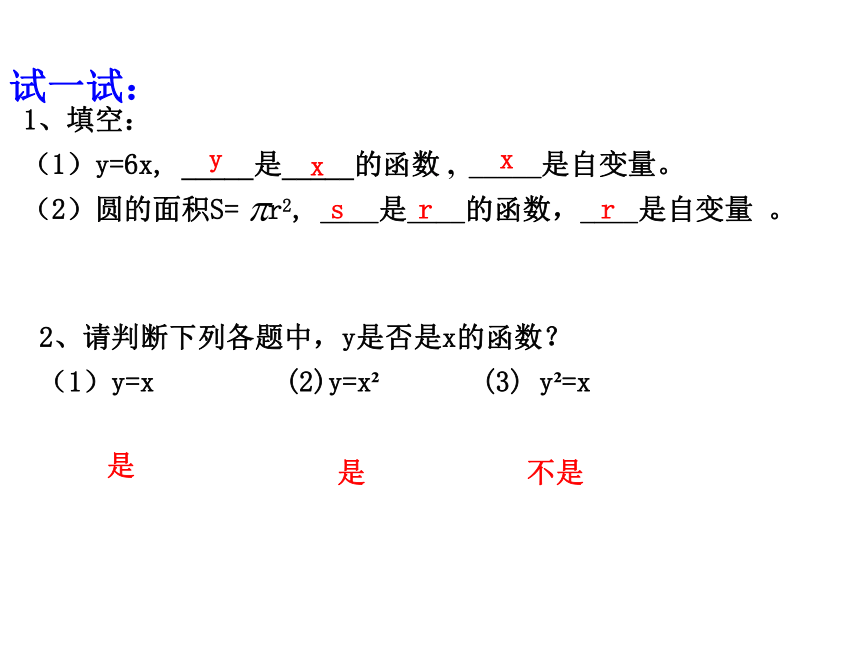
试一试:
1、填空:
(1)y=6x, _____是_____的函数 , _____是自变量。
(2)圆的面积S= r2, ____是____的函数,____是自变量 。
2、请判断下列各题中,y是否是x的函数?
(1)y=x (2)y=x (3) y =x
y
x
x
s
r
r
是
是
不是
2.数字游戏:用x表示左边的数字,用y表示右边的数字,那么变量y是否是变量x 的函数?
左边的数都减去2后得到右边的数
。。。
8
-8
-9
9
。。。
。。。
64
81
。。。
左边的数平方后得到右边的数
。。。
5
-5
-7
7
。。。
。。。
25
49
。。。
左边的数开方后得到右边的数
X≥0
。。。
8
3
-9
0
。。。
。。。
6
1
-11
-2
。。。
D
3、下列图形表示y是x的函数的是( )
x
y
0
x
y
0
x
y
0
A
B
C
D
x
y
0
4、下表表示的是y是x的函数吗?_____(填是或不是)
2
-1
2
1
2
y
5
1
0
-1
-2
x
是
2、观察下图,你知道当t=9时,T= ?
把t=6代入函数解析式,得m=16t=16×6=96
在这里,我们把m=96叫做当自变量t=6时的函数值。
1、对于函数m=16t,当t=6时,能求m的值吗?
怎么求?
请你思考
1
T=1叫做当自变量t=9时的函数值。
当t=14时,函数值为___。
5.13
4.77
4.14
3.6
年利率y(%)
五年
三年
二年
一年
时期x
3、观察上表,当x=3时,y= ;
4.77
y=4.77叫做当自变量x=3时的函数值。
5
代一代
画一画
查一查
1.已知油箱内装有30 千克的油,油从管道中均匀的以每分钟 0.5千克的速度流出,设油箱中剩余油量为Q(千克),流出时间为t(分钟).
(1) 写出Q 与t 之间的函数解析式?
(2)求当t=10时的函数值,并说明它的实际意义?
(3)t=100,行吗?为什么?
(4)你能说出自变量t的取值范围吗?
学以致用:
如图是德清县拔打市内电话收费情况,根据图象填空:
(1)通话2分钟的话费为_______元.
(2)通话3分钟内,话费为_______元,若超过3分钟,话费随时间的增加而______.
(3)通话费y可以看作时间t的函数吗
(4)求当t=4时的函数值,并说明它的实际意义
0
1
2
3
4
0.2
0.3
y(话费:元)
t(时间:分)
0.2
0.2
增加
可以
它的实际意义为通话4分钟的话费为0.3元.
解:当t=4时,函数值y=0.3,
下图是小明放学回家的折线图,其中t表示时间,s表示离开学校的路程。请根据图象回答下面的问题:
(1)路程s可以看成t的函数吗?_______(填“可以”或“不可以”)
(2)当t=5分时的函数值为________
(3)当10≤t≤15时,对应的函数值是_______, 它的实际意义
是________________________________
(4)学校离家的距离是___________,
小明放学骑自行车回家共
用了____________分钟.
做一做:
1千米
可以
2千米
小明回家的途中停留了5分钟
3.5千米
20
2、在国内投寄平信应付邮资如下表:
3.60
2.40
1.20
邮资y(元)
40<m≤60
20<m≤40
0<m≤20
信件质量m(克)
(1)若有四封信件质量分别为5克、10克、30克和50克,则该分别付邮资多少元?
(2) y是m的函数吗 为什么?
m(克) 5 10 30 50
y (元)
1.20
1.20
2.40
3.60
1、一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的________________,y都有____________,
那我们就说___是___的函数,其中x叫做________.
每一个确定的值
唯一确定的值
y
x
自变量
2、函数的三种常用表示方法是___________ , __________ ,__________
解析法
图象法
列表法
3、求函数值常用___________,___________,
___________的办法来求.
代一代
画一画
查一查
布置作业:
作业本(2)中的5.2(1)
小红的爷爷饭后出去散步,从家里出发走20分钟到一个离家900米的街心花园与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家距离y(米)与时间x(分)之间函数关系的是( )
y(米)
X(分)
20
40
o
900
A
y(米)
X(分)
20
40
o
900
B
y(米)
X(分)
20
40
o
900
y(米)
X(分)
20
40
o
900
C
D
D
认识函数
知识回顾:
在一个变化过程中,______________的量称为变量, ____________的量称为常量.
问题1、小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。常量是___________, 变量是_____________
16元/时
t时、m元
能用t的代数式表示m的值吗?
m=16t
如果t取一个确定值,那么m相应的取几个值?
对于变量t取一个确定的值,变量m相应的也取唯一确定的值.
可以取不同值
固定不变
如果时间t取某个特定的时间,温度T相应取几个值?
下图是钟管中心学校某天的气温变化图
问题2:
这个问题中有变量吗?
对于变量t取一个确定的值,变量T相应的也取唯一确定的值.
问题3:银行对不同的存款方式都规定了相应的利率,下表是银行调整的利率:
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
这个问题中有变量吗?
如果时期x取某个特定的时期,那么年利率y相应的取几个值?
对于变量x取一个确定的值,变量y相应的也取唯一确定的值.
这三个问题中都有2个变量,这两个变量有什么关系?
当其中一个变量取一个确定的值时,另一个变量相应的也取唯一确定的值。
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。
问题3:
问题2:
问题1:
问题1、小明是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明这个月工作的时间为t时,应得报酬为m元。则
m=16t
对于变量t的每一个确定的值,变量m都有唯一确定的值.
函数的概念:
一般地,在某个变化过程中,设有两个变量x和y,如果对于x的每一个确定的值,y相应的都有唯一确定的值,那我们就说y是x的函数,其中x叫做自变量。
注意:函数指的是两个变量之间的一种关系。
m是t的函数,t是自变量.
象m=16t这种表示函数关系的等式叫函数解析式,简称函数式。
m关于t的函数解析式
函数解析式的书写要求:通常等式的左边是表示函数一个字母.
,右边是含自变量的代数式。
用函数解析式表示函数的方法叫解析法。
问题2:
下图是钟管中心学校某天的气温变化图
对于变量t取一个确定的值,变量T也取唯一确定的值.
T是t的函数,t是自变量。
像这种用图象来表示两个变量之间函数关系的方法叫图象法。
问题3:银行对不同的存款方式都规定了相应的利率,下表是银行调整的利率:
时期x 一年 二年 三年 五年
年利率y(%) 3.6 4.14 4.77 5.13
对于变量x取一个确定的值,变量y也取唯一确定的值.
y是x的函数,x是自变量。
像这种把两个变量之间函数关系列成表格的形式的方法叫
列表法。
试一试:
1、填空:
(1)y=6x, _____是_____的函数 , _____是自变量。
(2)圆的面积S= r2, ____是____的函数,____是自变量 。
2、请判断下列各题中,y是否是x的函数?
(1)y=x (2)y=x (3) y =x
y
x
x
s
r
r
是
是
不是
2.数字游戏:用x表示左边的数字,用y表示右边的数字,那么变量y是否是变量x 的函数?
左边的数都减去2后得到右边的数
。。。
8
-8
-9
9
。。。
。。。
64
81
。。。
左边的数平方后得到右边的数
。。。
5
-5
-7
7
。。。
。。。
25
49
。。。
左边的数开方后得到右边的数
X≥0
。。。
8
3
-9
0
。。。
。。。
6
1
-11
-2
。。。
D
3、下列图形表示y是x的函数的是( )
x
y
0
x
y
0
x
y
0
A
B
C
D
x
y
0
4、下表表示的是y是x的函数吗?_____(填是或不是)
2
-1
2
1
2
y
5
1
0
-1
-2
x
是
2、观察下图,你知道当t=9时,T= ?
把t=6代入函数解析式,得m=16t=16×6=96
在这里,我们把m=96叫做当自变量t=6时的函数值。
1、对于函数m=16t,当t=6时,能求m的值吗?
怎么求?
请你思考
1
T=1叫做当自变量t=9时的函数值。
当t=14时,函数值为___。
5.13
4.77
4.14
3.6
年利率y(%)
五年
三年
二年
一年
时期x
3、观察上表,当x=3时,y= ;
4.77
y=4.77叫做当自变量x=3时的函数值。
5
代一代
画一画
查一查
1.已知油箱内装有30 千克的油,油从管道中均匀的以每分钟 0.5千克的速度流出,设油箱中剩余油量为Q(千克),流出时间为t(分钟).
(1) 写出Q 与t 之间的函数解析式?
(2)求当t=10时的函数值,并说明它的实际意义?
(3)t=100,行吗?为什么?
(4)你能说出自变量t的取值范围吗?
学以致用:
如图是德清县拔打市内电话收费情况,根据图象填空:
(1)通话2分钟的话费为_______元.
(2)通话3分钟内,话费为_______元,若超过3分钟,话费随时间的增加而______.
(3)通话费y可以看作时间t的函数吗
(4)求当t=4时的函数值,并说明它的实际意义
0
1
2
3
4
0.2
0.3
y(话费:元)
t(时间:分)
0.2
0.2
增加
可以
它的实际意义为通话4分钟的话费为0.3元.
解:当t=4时,函数值y=0.3,
下图是小明放学回家的折线图,其中t表示时间,s表示离开学校的路程。请根据图象回答下面的问题:
(1)路程s可以看成t的函数吗?_______(填“可以”或“不可以”)
(2)当t=5分时的函数值为________
(3)当10≤t≤15时,对应的函数值是_______, 它的实际意义
是________________________________
(4)学校离家的距离是___________,
小明放学骑自行车回家共
用了____________分钟.
做一做:
1千米
可以
2千米
小明回家的途中停留了5分钟
3.5千米
20
2、在国内投寄平信应付邮资如下表:
3.60
2.40
1.20
邮资y(元)
40<m≤60
20<m≤40
0<m≤20
信件质量m(克)
(1)若有四封信件质量分别为5克、10克、30克和50克,则该分别付邮资多少元?
(2) y是m的函数吗 为什么?
m(克) 5 10 30 50
y (元)
1.20
1.20
2.40
3.60
1、一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的________________,y都有____________,
那我们就说___是___的函数,其中x叫做________.
每一个确定的值
唯一确定的值
y
x
自变量
2、函数的三种常用表示方法是___________ , __________ ,__________
解析法
图象法
列表法
3、求函数值常用___________,___________,
___________的办法来求.
代一代
画一画
查一查
布置作业:
作业本(2)中的5.2(1)
小红的爷爷饭后出去散步,从家里出发走20分钟到一个离家900米的街心花园与朋友聊天10分钟后,用15分钟返回家里.下面图形中表示小红爷爷离家距离y(米)与时间x(分)之间函数关系的是( )
y(米)
X(分)
20
40
o
900
A
y(米)
X(分)
20
40
o
900
B
y(米)
X(分)
20
40
o
900
y(米)
X(分)
20
40
o
900
C
D
D
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
