7.4一次函数的图像(2)

(共10张PPT)
7.4一次函数的图像（2）
知识回顾：
1.一次函数y=kx+b的图象是 。
2.一次函数y=kx+b的图象与 x轴的交点是 ；
与 y轴的交点是 。
当为正比例函数时，与 x轴的交点是 ；
与 y轴的交点是 。
3.一次函数y=kx+b的图象，
当b>0时，与 y轴的交点在 x轴的 ；
当b<0时，与 y轴的交点在 x轴的 。
一条直线
（0，b）
（0，0）
（0，0）
上方
下方
合作学习：
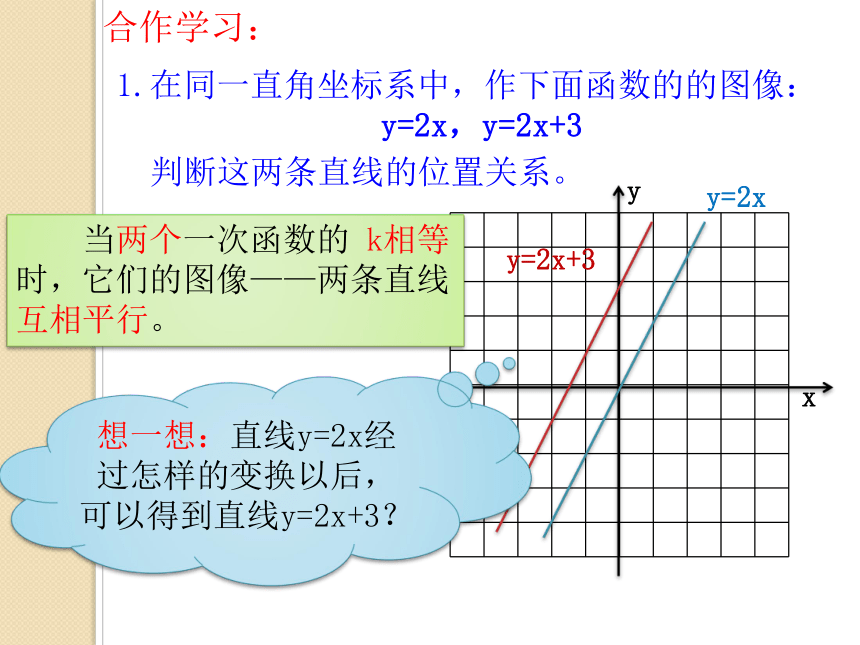
1.在同一直角坐标系中，作下面函数的的图像：
y=2x，y=2x+3
判断这两条直线的位置关系。
x
y
y=2x+3
y=2x
当两个一次函数的 k相等时，它们的图像——两条直线互相平行。
想一想：直线y=2x经过怎样的变换以后，可以得到直线y=2x+3？
合作学习：
2.在同一直角坐标系中，作下面函数的的图像：
y=2x+3，y=-2x+3，
从左向右，观察图像的走势，根据函数解析式的特征，将它们分类。
x
y
y=2x+3
y=2x+3，y=-2x+3，
y=-2x+3
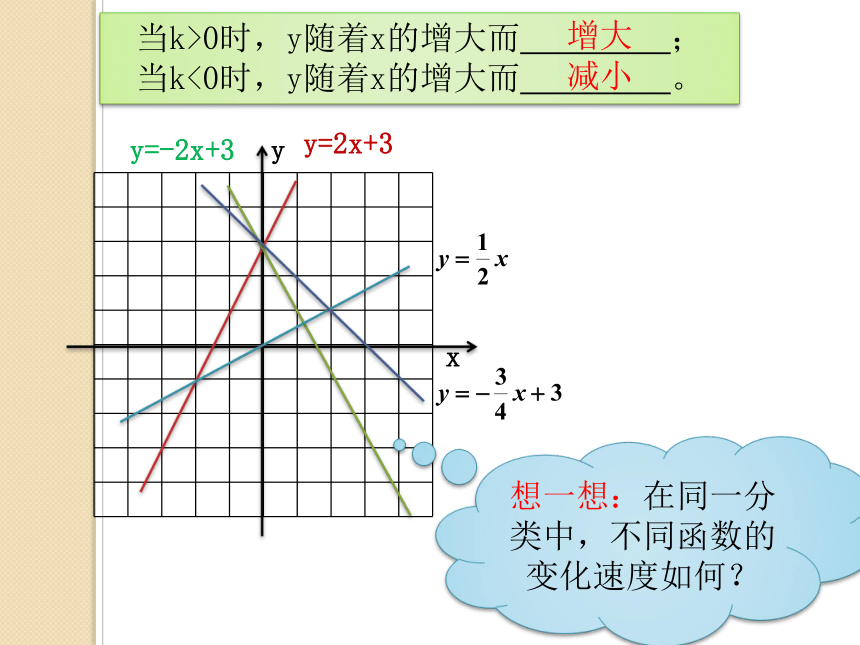
当k>0时，y随着x的增大而 ；
当k<0时，y随着x的增大而 。
想一想：在同一分类中，不同函数的变化速度如何？
增大
减小
例1：填写下表，并回答问题。
y=kx+b b 0 b 0
k 0 在 象限 在 象限
k 0 在 象限 在 象限
P、Q在直线 y=0.5x上，且x2>x1， 则y2 y1；
P、Q在直线 y=-0.75x+3上，且y2设P(x1, y1)
Q(x2, y2)
>
<
<
>
>
>
练1：点(0,y1 )、 (-1,y2 ) 、(4,y3 )在一次函数
y=-3x+m的图像上，则y1，y2，y3的大小关系是 。
练2：在一次函数 y=-4x+5的图像上，当-1≤x<4时，对应的函数值的取值范围是 。
例2：已知直线 y=kx+k2-2与直线 y=3x+1交于 y轴上同一点。
（1）求k的值；
（2）请说明，这时的直线 y=kx+k2-2从左到右的变化情况。
例3：已知y是关于x的一次函数，这个函数的图像上有两点的坐标分别为（2，5），（-3，20）。
（1）求当 -4（2）判断当 2小结：
正比例函数：
必经过 ；
当k>0时，y随着x的增大而 ； 当k<0时，y随着x的增大而 。
一次函数：
当b>0时，与 y轴的交点在 x轴的 ； 当b<0时，与 y轴的交点在 x轴的 。
当k>0时，y随着x的增大而 ； 当k<0时，y随着x的增大而 。
，变化速度越快。
取值范围的互推：
图象法；
函数增减性（最大值、最小值）
（0，0）
增大
增大
减小
减小
上方
下方
K的绝对值越大