浙教版九年级数学上册3.7 正多边形 同步练习(Word版含答案)
文档属性
| 名称 | 浙教版九年级数学上册3.7 正多边形 同步练习(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-07 00:00:00 | ||
图片预览



文档简介
3.7
正多边形
一.选择题
1.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
2.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
3.一元钱硬币的直径约为24mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12mm
B.12mm
C.6mm
D.6mm
4.如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是( )
A.60°
B.70°
C.72°
D.144°
5.已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是( )
A.2
B.1
C.
D.
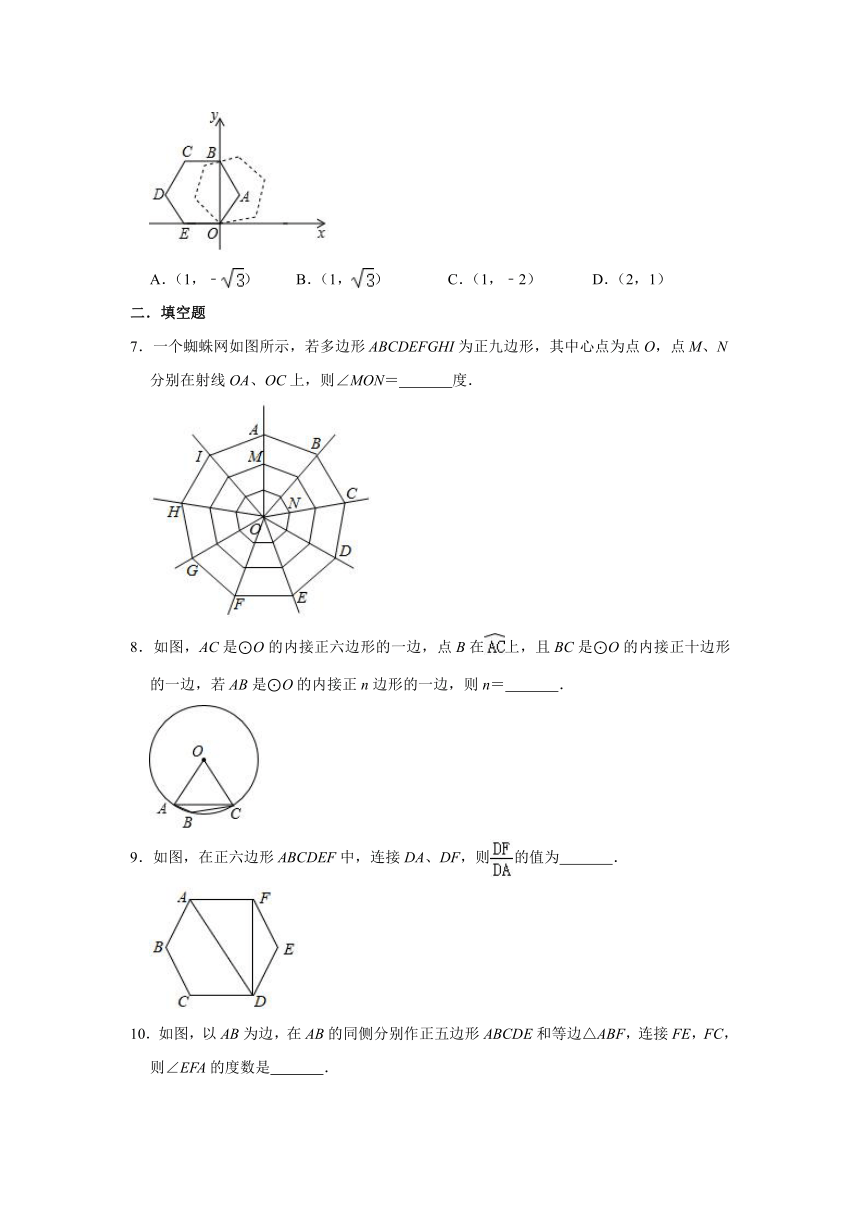
6.如图,在平面直角坐标系中,将边长为1的正六边形OABCDE绕点O顺时针旋转i个45°,得到正六边形OAiBi?iDiEi,则正六边形OAiBi?iDiEi(i=2020)的顶点?i的坐标是( )
A.(1,﹣)
B.(1,)
C.(1,﹣2)
D.(2,1)
二.填空题
7.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则∠MON=
度.
8.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边,若AB是⊙O的内接正n边形的一边,则n=
.
9.如图,在正六边形ABCDEF中,连接DA、DF,则的值为
.
10.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是
.
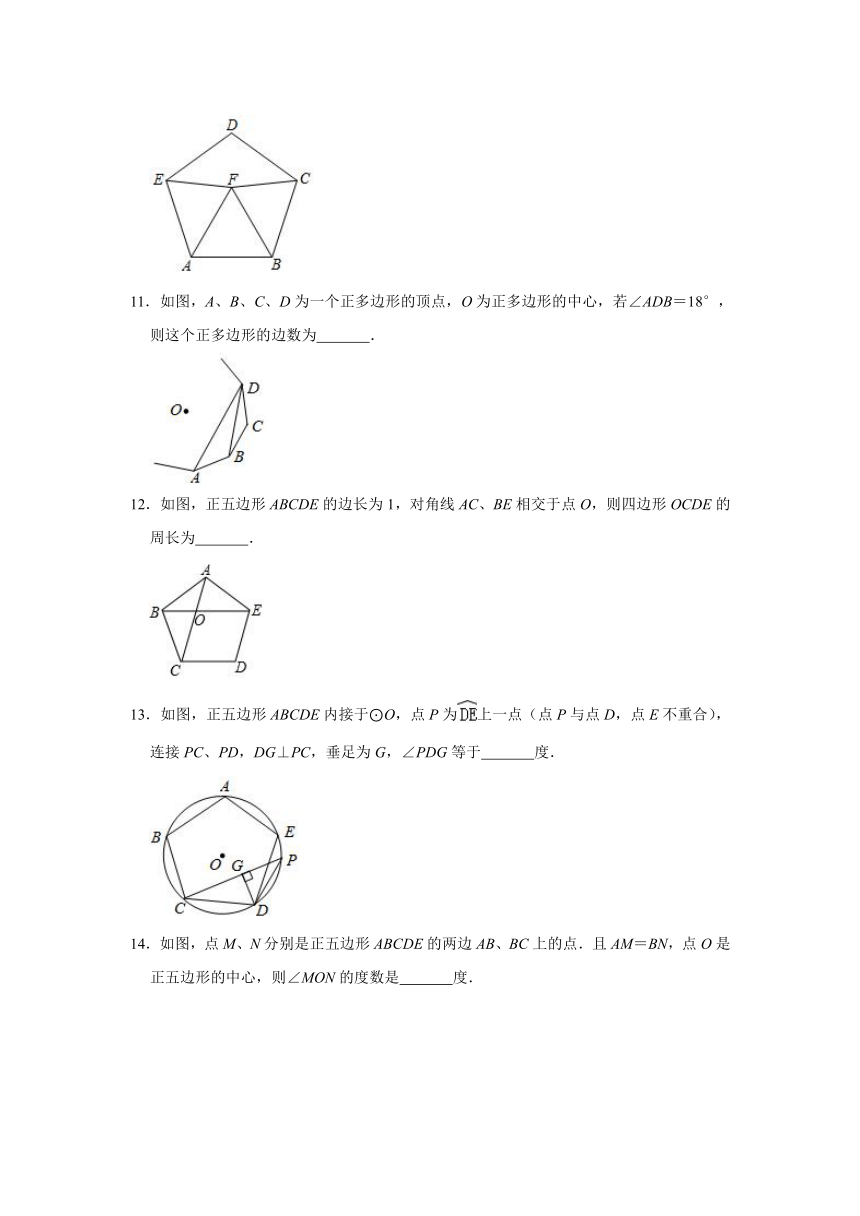
11.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为
.
12.如图,正五边形ABCDE的边长为1,对角线AC、BE相交于点O,则四边形OCDE的周长为
.
13.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于
度.
14.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
三.解答题
15.如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;
(1)AC∥DE;
(2)ME=AE.
16.如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;
(2)连接OF、OG,求∠OGF.
17.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°,试说明:∠NOC=60°
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么∠DON=
度,并说明理由.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=
,且∠EON=
度.(正n边形内角和(n﹣2)×180°,正多边形各内角相等)
参考答案
一.选择题
1.解:设圆的半径为R,
则正三角形的边心距为a=R×cos60°=R.
四边形的边心距为b=R×cos45°=R,
正六边形的边心距为c=R×cos30°=R.
∵RRR,
∴a<b<c,
故选:A.
2.解:∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°﹣120°)=30°,
故选:A.
3.解:已知圆内接半径r为12mm,
则OB=12,
∴BD=OB?sin30°=12×=6,
则BC=2×6=12,
可知边长为12mm,就是完全覆盖住的正六边形的边长最大.
故选:A.
4.解:∵五边形ABCDE为正五边形,
∴∠ABC=∠C==108°,
∵CD=CB,
∴∠CBD==36°,
∴∠ABD=∠ABC﹣∠CBD=72°,
故选:C.
5.解:如图(1),
O为△ABC的中心,
AD为△ABC的边BC上的高,
则OD为边心距,
∴∠BAD=30°,
又∵AO=BO,
∴∠ABO=∠BAD=30°,
∴∠OBD=60°﹣30°=30°,
在Rt△OBD中,
BO=2DO,
即AO=2DO,
∴OD:OA:AD=1:2:3.
在正△ABC中,AD是高,设BD=x,则AD=BD?tan60°=BD=x.
∵正三角形ABC面积为cm2,
∴BC?AD=,
∴×2x?x=,
∴x=1.
即BD=1,则AD=,
∵OD:OA:AD=1:2:3,
∴AO=cm.
即这个圆的半径为cm.
所以该圆的内接正六边形的边心距×sin60°=,
故选:B.
6.解:由题意旋转8次应该循环,
∵2020÷8=252…4,
∴?i的坐标与C4的坐标相同,
∵C(﹣1,),点C与C4关于原点对称,
∴C4(1,﹣),
∴顶点?i的坐标是(1,﹣),
故选:A.
二.填空题
7.解:根据正多边形性质得,中心角为:
∠AOB=360°÷9=40°,
∴∠MON=2∠AOB=80°.
故答案为:80.
8.解:连接BO,
∵AC是⊙O内接正六边形的一边,
∴∠AOC=360°÷6=60°,
∵BC是⊙O内接正十边形的一边,
∴∠BOC=360°÷10=36°,
∴∠AOB=∠AOC﹣∠BOC=60°﹣36°=24°,
∴n=360°÷24°=15;
故答案为:15.
9.解:∵六边形ABCDEF是正六边形,
∴EF=ED,∠AFE=∠FED=∠EDC=120°,
∴∠EFD=∠EDF=30°,
∴∠AFD=90°,
∵∠ADC=∠ADE=60°,
∴∠ADF=30°,
∴=cos∠ADF=,
故答案为:.
10.解:∵正五边形ABCDE,
∴∠EAB==108°,
∵△ABF是等边三角形,
∴∠FAB=60°,
∴∠EAF=108°﹣60°=48°,
∵AE=AF,
∴∠AEF=∠AFE=(180°﹣48°)=66°,
故答案为:66°.
11.解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10,
故答案为:10.
12.解:∵五边形ABCDE是正五边形,
∴CD=DE=AB=1,∠BAE=∠BCD=∠D=×(5﹣2)×180°=108°,
∠BAO=∠BCA=∠ABE=∠AEB=×(180°﹣108°)=36°,
∴∠BED=108°﹣36°=72°,
∴∠D+∠BED=180°,
∴BE∥CD;同理可证DE∥AC,
∴四边形DEOC为平行四边形,而DE=DC,
∴四边形CDEO是菱形,
∵正五边形的边长为1,
∴CD=DE=1,
∴四边形OCDE的周长为4,
故答案为:4.
13.解:连接OC、OD,如图所示:
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣∠CPD=90°﹣36°=54°,
故答案为:54.
14.解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
三.解答题
15.证明:(1)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AB=BC,
∴∠CAB=∠BCA=36°,
∴∠EAC=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE;
(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AE=AB,
∴∠AEB=∠ABE=36°,
∵∠EAC=72°,
∴∠EMA=180°﹣36°﹣72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
16.解:(1)设正六边形的边长为a,
则三角形OEF的边EF上的高为a,
则正六边形的面积为:6××a×a=a2,
∴正方形的面积为:a×a=a2,
∴正六边形与正方形的面积比a2:a2=3:2;
(2)∵OF=EF=FG,
∴∠OGF=(180°﹣60°﹣90°)=15°.
17.(1)证明:∵△ABC是正三角形,
∴∠A=∠ABC=60°,AB=BC,
在△ABN和△BCM中,,
∴△ABN≌△BCM(SAS),
∴∠ABN=∠BCM,
又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∴∠NOC=60°;
(2)解:∵四边形ABCD是正方形,
∴∠DAM=∠ABN=90°,AD=AB,
又∵AM=BN,
∴△ABN≌△DAM(SAS),
∴AN=DM,∠ADM=∠BAN,
又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°
∴∠AOM=90°;即∠DON=90°;
(3)解:∵五边形ABCDE是正五边形,
∴∠A=∠B,AB=AE,
又∵AM=BN,
∴△ABN≌△EAM(SAS),
∴AN=ME,
∴∠AEM=∠BAN,
∴∠NOE=∠NAE+∠AEM=∠NAE+∠BAN=∠BAE=108°.
故答案为:90°,EM,108°.
正多边形
一.选择题
1.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a,b,c,则a,b,c的大小关系是( )
A.a<b<c
B.b<a<c
C.a<c<b
D.c<b<a
2.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
3.一元钱硬币的直径约为24mm,则用它能完全覆盖住的正六边形的边长最大不能超过( )
A.12mm
B.12mm
C.6mm
D.6mm
4.如图,已知正五边形ABCDE内接于⊙O,连结BD,则∠ABD的度数是( )
A.60°
B.70°
C.72°
D.144°
5.已知圆内接正三角形的面积为,则该圆的内接正六边形的边心距是( )
A.2
B.1
C.
D.
6.如图,在平面直角坐标系中,将边长为1的正六边形OABCDE绕点O顺时针旋转i个45°,得到正六边形OAiBi?iDiEi,则正六边形OAiBi?iDiEi(i=2020)的顶点?i的坐标是( )
A.(1,﹣)
B.(1,)
C.(1,﹣2)
D.(2,1)
二.填空题
7.一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则∠MON=
度.
8.如图,AC是⊙O的内接正六边形的一边,点B在上,且BC是⊙O的内接正十边形的一边,若AB是⊙O的内接正n边形的一边,则n=
.
9.如图,在正六边形ABCDEF中,连接DA、DF,则的值为
.
10.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是
.
11.如图,A、B、C、D为一个正多边形的顶点,O为正多边形的中心,若∠ADB=18°,则这个正多边形的边数为
.
12.如图,正五边形ABCDE的边长为1,对角线AC、BE相交于点O,则四边形OCDE的周长为
.
13.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC、PD,DG⊥PC,垂足为G,∠PDG等于
度.
14.如图,点M、N分别是正五边形ABCDE的两边AB、BC上的点.且AM=BN,点O是正五边形的中心,则∠MON的度数是
度.
三.解答题
15.如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;
(1)AC∥DE;
(2)ME=AE.
16.如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
(1)求正六边形与正方形的面积比;
(2)连接OF、OG,求∠OGF.
17.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°,试说明:∠NOC=60°
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么∠DON=
度,并说明理由.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN=
,且∠EON=
度.(正n边形内角和(n﹣2)×180°,正多边形各内角相等)
参考答案
一.选择题
1.解:设圆的半径为R,
则正三角形的边心距为a=R×cos60°=R.
四边形的边心距为b=R×cos45°=R,
正六边形的边心距为c=R×cos30°=R.
∵RRR,
∴a<b<c,
故选:A.
2.解:∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°﹣120°)=30°,
故选:A.
3.解:已知圆内接半径r为12mm,
则OB=12,
∴BD=OB?sin30°=12×=6,
则BC=2×6=12,
可知边长为12mm,就是完全覆盖住的正六边形的边长最大.
故选:A.
4.解:∵五边形ABCDE为正五边形,
∴∠ABC=∠C==108°,
∵CD=CB,
∴∠CBD==36°,
∴∠ABD=∠ABC﹣∠CBD=72°,
故选:C.
5.解:如图(1),
O为△ABC的中心,
AD为△ABC的边BC上的高,
则OD为边心距,
∴∠BAD=30°,
又∵AO=BO,
∴∠ABO=∠BAD=30°,
∴∠OBD=60°﹣30°=30°,
在Rt△OBD中,
BO=2DO,
即AO=2DO,
∴OD:OA:AD=1:2:3.
在正△ABC中,AD是高,设BD=x,则AD=BD?tan60°=BD=x.
∵正三角形ABC面积为cm2,
∴BC?AD=,
∴×2x?x=,
∴x=1.
即BD=1,则AD=,
∵OD:OA:AD=1:2:3,
∴AO=cm.
即这个圆的半径为cm.
所以该圆的内接正六边形的边心距×sin60°=,
故选:B.
6.解:由题意旋转8次应该循环,
∵2020÷8=252…4,
∴?i的坐标与C4的坐标相同,
∵C(﹣1,),点C与C4关于原点对称,
∴C4(1,﹣),
∴顶点?i的坐标是(1,﹣),
故选:A.
二.填空题
7.解:根据正多边形性质得,中心角为:
∠AOB=360°÷9=40°,
∴∠MON=2∠AOB=80°.
故答案为:80.
8.解:连接BO,
∵AC是⊙O内接正六边形的一边,
∴∠AOC=360°÷6=60°,
∵BC是⊙O内接正十边形的一边,
∴∠BOC=360°÷10=36°,
∴∠AOB=∠AOC﹣∠BOC=60°﹣36°=24°,
∴n=360°÷24°=15;
故答案为:15.
9.解:∵六边形ABCDEF是正六边形,
∴EF=ED,∠AFE=∠FED=∠EDC=120°,
∴∠EFD=∠EDF=30°,
∴∠AFD=90°,
∵∠ADC=∠ADE=60°,
∴∠ADF=30°,
∴=cos∠ADF=,
故答案为:.
10.解:∵正五边形ABCDE,
∴∠EAB==108°,
∵△ABF是等边三角形,
∴∠FAB=60°,
∴∠EAF=108°﹣60°=48°,
∵AE=AF,
∴∠AEF=∠AFE=(180°﹣48°)=66°,
故答案为:66°.
11.解:连接OA,OB,
∵A、B、C、D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=18°,
∴∠AOB=2∠ADB=36°,
∴这个正多边形的边数==10,
故答案为:10.
12.解:∵五边形ABCDE是正五边形,
∴CD=DE=AB=1,∠BAE=∠BCD=∠D=×(5﹣2)×180°=108°,
∠BAO=∠BCA=∠ABE=∠AEB=×(180°﹣108°)=36°,
∴∠BED=108°﹣36°=72°,
∴∠D+∠BED=180°,
∴BE∥CD;同理可证DE∥AC,
∴四边形DEOC为平行四边形,而DE=DC,
∴四边形CDEO是菱形,
∵正五边形的边长为1,
∴CD=DE=1,
∴四边形OCDE的周长为4,
故答案为:4.
13.解:连接OC、OD,如图所示:
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣∠CPD=90°﹣36°=54°,
故答案为:54.
14.解:连接OA、OB、OC,
∠AOB==72°,
∵∠AOB=∠BOC,OA=OB,OB=OC,
∴∠OAB=∠OBC,
在△AOM和△BON中,
∴△AOM≌△BON,
∴∠BON=∠AOM,
∴∠MON=∠AOB=72°,
故答案为:72.
三.解答题
15.证明:(1)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AB=BC,
∴∠CAB=∠BCA=36°,
∴∠EAC=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴AC∥DE;
(2)∵五边形ABCDE是正五边形,
∴∠ABC=∠EAB=∠DCB=∠DEA==108°,AE=AB,
∴∠AEB=∠ABE=36°,
∵∠EAC=72°,
∴∠EMA=180°﹣36°﹣72°=72°,
∴∠EAM=∠EMA,
∴ME=AE.
16.解:(1)设正六边形的边长为a,
则三角形OEF的边EF上的高为a,
则正六边形的面积为:6××a×a=a2,
∴正方形的面积为:a×a=a2,
∴正六边形与正方形的面积比a2:a2=3:2;
(2)∵OF=EF=FG,
∴∠OGF=(180°﹣60°﹣90°)=15°.
17.(1)证明:∵△ABC是正三角形,
∴∠A=∠ABC=60°,AB=BC,
在△ABN和△BCM中,,
∴△ABN≌△BCM(SAS),
∴∠ABN=∠BCM,
又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∴∠NOC=60°;
(2)解:∵四边形ABCD是正方形,
∴∠DAM=∠ABN=90°,AD=AB,
又∵AM=BN,
∴△ABN≌△DAM(SAS),
∴AN=DM,∠ADM=∠BAN,
又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°
∴∠AOM=90°;即∠DON=90°;
(3)解:∵五边形ABCDE是正五边形,
∴∠A=∠B,AB=AE,
又∵AM=BN,
∴△ABN≌△EAM(SAS),
∴AN=ME,
∴∠AEM=∠BAN,
∴∠NOE=∠NAE+∠AEM=∠NAE+∠BAN=∠BAE=108°.
故答案为:90°,EM,108°.
同课章节目录
