2020-2021学年浙教版九年级数学第四章相似三角形4.1∽4.4综合提高卷(word版附答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级数学第四章相似三角形4.1∽4.4综合提高卷(word版附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 377.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-08 12:58:25 | ||
图片预览



文档简介
2020-2021学年浙教版九年级数学第四章《相似三角形》4.1∽4.4综合提高卷
班级:
_________
姓名:
_________
成绩
_________
一、选择题(每题3分,共30分)
1.已知5x
=
6y(y≠0),则下列比例式中,正确的是
(
)
A.
=
B.
=
C.
=
D.
=
2.已知一本书的宽与长之比为黄金比,书的长为14
cm,则它的宽为
(
)
A.(7
+
7)cm
B.(21
-
7)cm
C.(7
-
7)cm
D.(7
-
21)cm
3.如图所示,AB∥CD∥EF,AF,BE交于点G,下列比例式中,错误的是
(
)
A.
=
B.
=
C.
=
D.
=
4.如图所示,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE
=
9,
=
,则EC的长是
( )
A.4.5
B.8
C.12
D.14
5.如图所示,以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,则这两个三角形的相似比为
(
)
A.2:1
B.3:1
C.4:3
D.3:2
6.如图所示,在四边形ABCD中,∠ADC
=
∠BAC,下列条件中,不能判定△ADC
∽△BAC的为(
)
A.∠DAC
=
∠ABC
B.AC平分∠BCD
C.AC2
=
BC·CD
D.
=
7.如图所示,点D,E,F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式中,不成立的是(
)
A.
=
B.
=
C.
=
D.
=
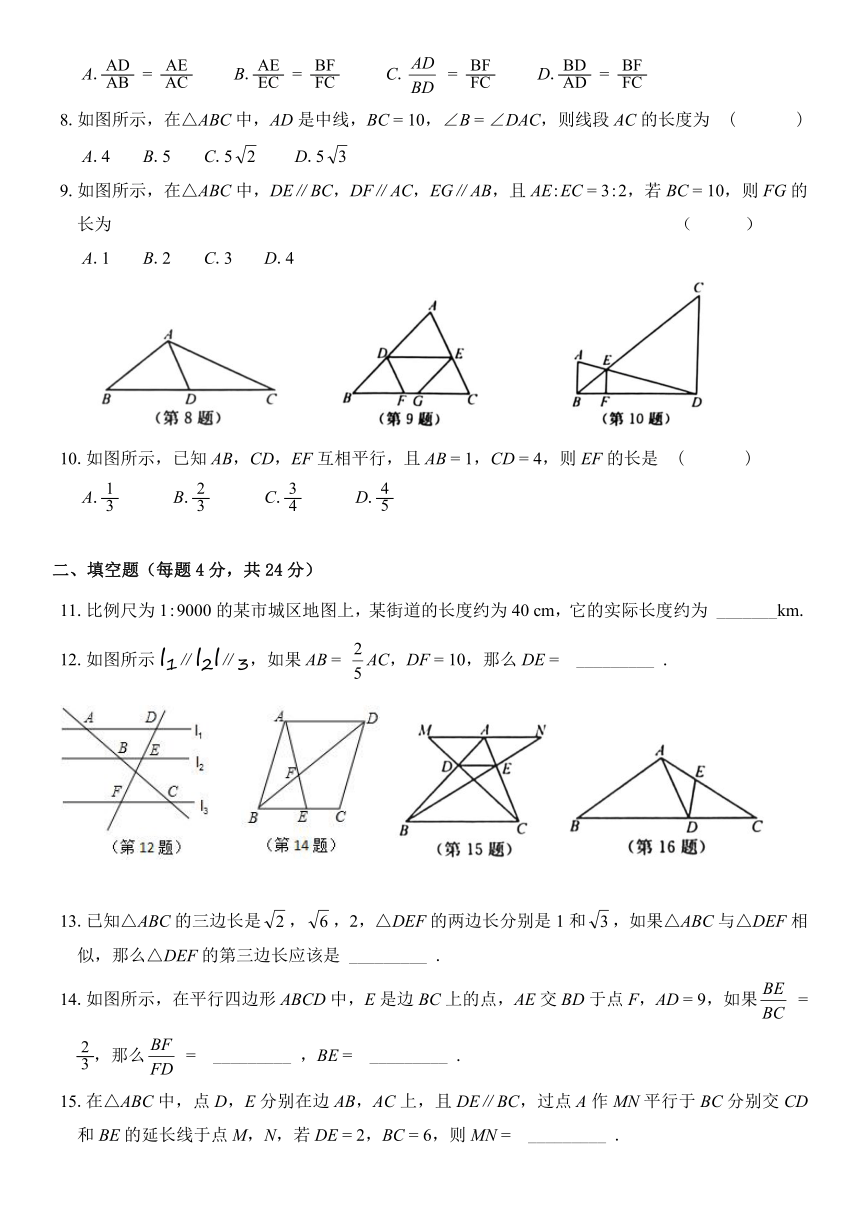
8.如图所示,在△ABC中,AD是中线,BC
=
10,∠B
=
∠DAC,则线段AC的长度为
(
)
A.4
B.5
C.5
D.5
9.如图所示,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC
=
3:2,若BC
=
10,则FG的长为
( )
A.1
B.2
C.3
D.4
10.如图所示,已知AB,CD,EF互相平行,且AB
=
1,CD
=
4,则EF的长是
(
)
A.
B.
C.
D.
二、填空题(每题4分,共24分)
11.比例尺为1:9000的某市城区地图上,某街道的长度约为40
cm,它的实际长度约为
_______km.
12.如图所示l1∥l2l∥3,如果AB
=
AC,DF
=
10,那么DE
=
_________
.
13.已知△ABC的三边长是,,2,△DEF的两边长分别是1和,如果△ABC与△DEF相似,那么△DEF的第三边长应该是
_________
.
14.如图所示,在平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD
=
9,如果
=
,那么
=
_________
,BE
=
_________
.
15.在△ABC中,点D,E分别在边AB,AC上,且DE∥BC,过点A作MN平行于BC分别交CD和BE的延长线于点M,N,若DE
=
2,BC
=
6,则MN
=
_________
.
16.如图所示,在△ABC中,AB
=
AC
=
10,BC
=
16,D,E分别是BC,AC边上的点,且∠ADE
=
∠B,EA
=
DE,则BD
=
_________
.
三、解答题(共66分)
17.(6分)已知线段a
=
0.3
m,b
=
60
cm,c
=
12
dm.
(1)求线段a与线段b的长度的比.
(2)如果线段a,b,c,d的长度成比例,求线段d的长.
18.(8分)如图所示,F是
ABCD的边AD上一点,延长CF交BA的延长线于点E.若=
,AB
=
4,求AE的长.
19.(8分)如图所示,F为
ABCD中DC边上的点,连结AF并延长,交BC的延长线于点E,交BD于点G,求证:AG2
=
FG·EG.
20.(10分)如图所示,在△ABC中,D是AB边上一点,过点D作DE∥BC,交AC于点E,F是DE延长线上一点,连结AF.
(1)若
=
,DE
=
6,求边BC的长.
(2)若∠FAE
=
∠B,FA
=
6,FE
=
4,求DF的长.
21.(10分)如图所示,在等腰三角形ABC中,AB
=
AC
=
5a,BC
=
8a,点D,E为边AB,BC上两点.
(1)若BD
=
AD,BE
=
CE,求DE的长.(用含a的代数式表示)
(2)若BD
=
2a,当△DBE中有一个角等于∠BAC,求此时DE的长.(用含a的代数式表示)
22.(12分)如图所示,在△ABC中,∠ACB
=
90°,AB
=
10,BC
=
6,点D在AB的延长线上,且BD
=
6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径.
(2)设CD交⊙O于点Q,
①试说明Q为CD的中点.
②求BQ·BE的值.
23.(12分)
(1)如图1所示,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)已知在△ABC中,∠BAC
=
90°,正方形DEFG的四个顶点在△ABC的边上,连结AG,AF,分别交DE于M,N两点.
①如图2所示,若AB
=
AC
=
1,直接写出MN的长.
②如图3所示,求证:MN
2
=
DM·EN.
班级:
_________
姓名:
_________
成绩
_________
一、选择题(每题3分,共30分)
1.已知5x
=
6y(y≠0),则下列比例式中,正确的是
(
)
A.
=
B.
=
C.
=
D.
=
2.已知一本书的宽与长之比为黄金比,书的长为14
cm,则它的宽为
(
)
A.(7
+
7)cm
B.(21
-
7)cm
C.(7
-
7)cm
D.(7
-
21)cm
3.如图所示,AB∥CD∥EF,AF,BE交于点G,下列比例式中,错误的是
(
)
A.
=
B.
=
C.
=
D.
=
4.如图所示,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE
=
9,
=
,则EC的长是
( )
A.4.5
B.8
C.12
D.14
5.如图所示,以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,则这两个三角形的相似比为
(
)
A.2:1
B.3:1
C.4:3
D.3:2
6.如图所示,在四边形ABCD中,∠ADC
=
∠BAC,下列条件中,不能判定△ADC
∽△BAC的为(
)
A.∠DAC
=
∠ABC
B.AC平分∠BCD
C.AC2
=
BC·CD
D.
=
7.如图所示,点D,E,F分别在△ABC的边上,且DE∥BC,EF∥AB,下列等式中,不成立的是(
)
A.
=
B.
=
C.
=
D.
=
8.如图所示,在△ABC中,AD是中线,BC
=
10,∠B
=
∠DAC,则线段AC的长度为
(
)
A.4
B.5
C.5
D.5
9.如图所示,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC
=
3:2,若BC
=
10,则FG的长为
( )
A.1
B.2
C.3
D.4
10.如图所示,已知AB,CD,EF互相平行,且AB
=
1,CD
=
4,则EF的长是
(
)
A.
B.
C.
D.
二、填空题(每题4分,共24分)
11.比例尺为1:9000的某市城区地图上,某街道的长度约为40
cm,它的实际长度约为
_______km.
12.如图所示l1∥l2l∥3,如果AB
=
AC,DF
=
10,那么DE
=
_________
.
13.已知△ABC的三边长是,,2,△DEF的两边长分别是1和,如果△ABC与△DEF相似,那么△DEF的第三边长应该是
_________
.
14.如图所示,在平行四边形ABCD中,E是边BC上的点,AE交BD于点F,AD
=
9,如果
=
,那么
=
_________
,BE
=
_________
.
15.在△ABC中,点D,E分别在边AB,AC上,且DE∥BC,过点A作MN平行于BC分别交CD和BE的延长线于点M,N,若DE
=
2,BC
=
6,则MN
=
_________
.
16.如图所示,在△ABC中,AB
=
AC
=
10,BC
=
16,D,E分别是BC,AC边上的点,且∠ADE
=
∠B,EA
=
DE,则BD
=
_________
.
三、解答题(共66分)
17.(6分)已知线段a
=
0.3
m,b
=
60
cm,c
=
12
dm.
(1)求线段a与线段b的长度的比.
(2)如果线段a,b,c,d的长度成比例,求线段d的长.
18.(8分)如图所示,F是
ABCD的边AD上一点,延长CF交BA的延长线于点E.若=
,AB
=
4,求AE的长.
19.(8分)如图所示,F为
ABCD中DC边上的点,连结AF并延长,交BC的延长线于点E,交BD于点G,求证:AG2
=
FG·EG.
20.(10分)如图所示,在△ABC中,D是AB边上一点,过点D作DE∥BC,交AC于点E,F是DE延长线上一点,连结AF.
(1)若
=
,DE
=
6,求边BC的长.
(2)若∠FAE
=
∠B,FA
=
6,FE
=
4,求DF的长.
21.(10分)如图所示,在等腰三角形ABC中,AB
=
AC
=
5a,BC
=
8a,点D,E为边AB,BC上两点.
(1)若BD
=
AD,BE
=
CE,求DE的长.(用含a的代数式表示)
(2)若BD
=
2a,当△DBE中有一个角等于∠BAC,求此时DE的长.(用含a的代数式表示)
22.(12分)如图所示,在△ABC中,∠ACB
=
90°,AB
=
10,BC
=
6,点D在AB的延长线上,且BD
=
6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径.
(2)设CD交⊙O于点Q,
①试说明Q为CD的中点.
②求BQ·BE的值.
23.(12分)
(1)如图1所示,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P,求证:=.
(2)已知在△ABC中,∠BAC
=
90°,正方形DEFG的四个顶点在△ABC的边上,连结AG,AF,分别交DE于M,N两点.
①如图2所示,若AB
=
AC
=
1,直接写出MN的长.
②如图3所示,求证:MN
2
=
DM·EN.
同课章节目录
