3.2三角形的内切圆

(共25张PPT)
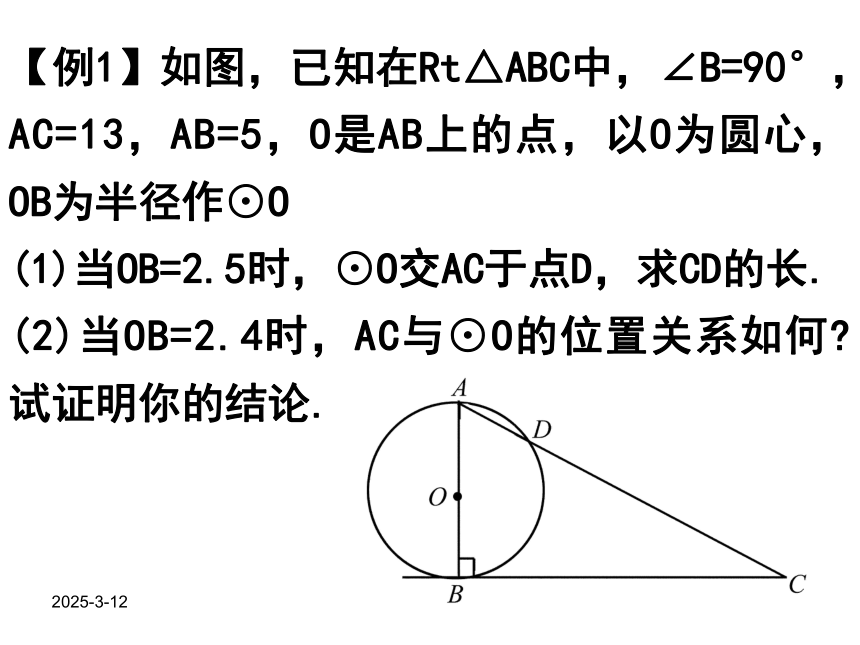
【例1】如图，已知在Rt△ABC中，∠B=90°，AC=13，AB=5，O是AB上的点，以O为圆心，OB为半径作⊙O
(1)当OB=2.5时，⊙O交AC于点D，求CD的长.
(2)当OB=2.4时，AC与⊙O的位置关系如何 试证明你的结论.
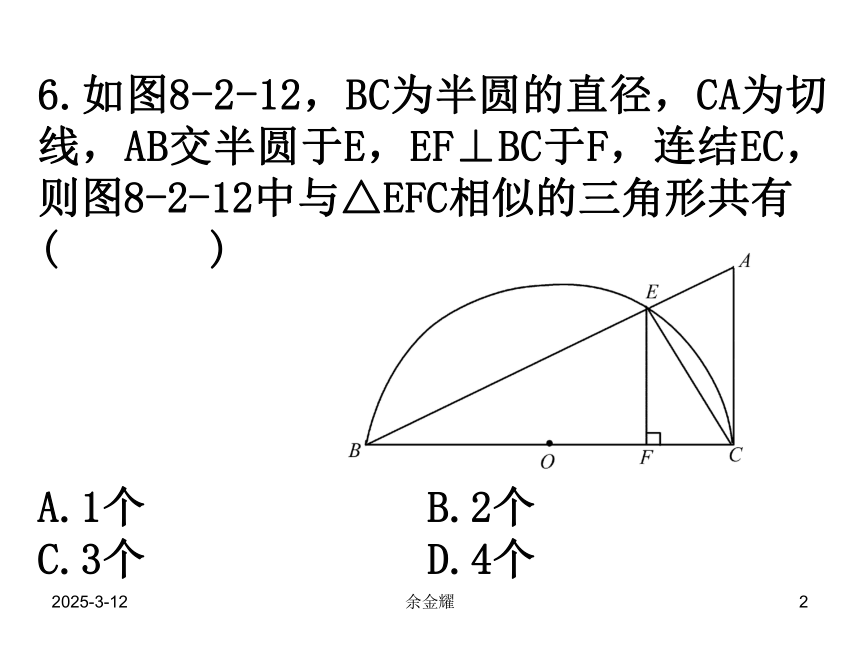
6.如图8-2-12，BC为半圆的直径，CA为切线，AB交半圆于E，EF⊥BC于F，连结EC，则图8-2-12中与△EFC相似的三角形共有
( )
A.1个 B.2个
C.3个 D.4个
三角形的内切圆
重点内容
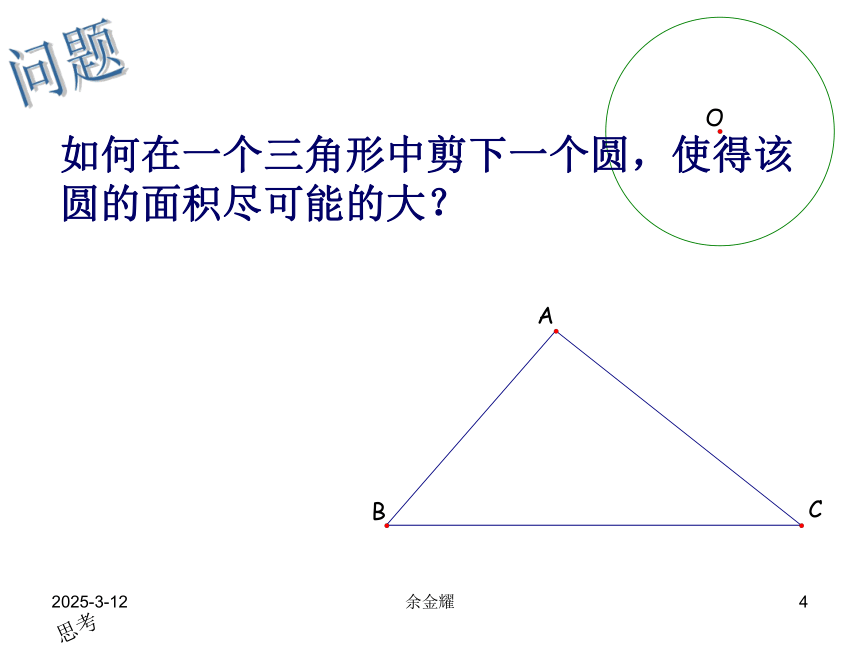
如何在一个三角形中剪下一个圆，使得该圆的面积尽可能的大？
思考
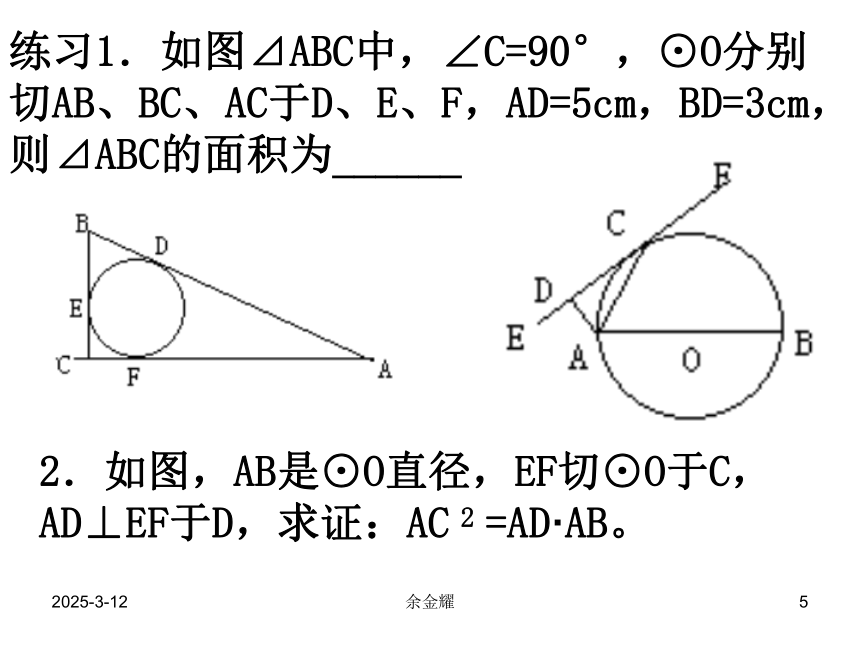
练习1．如图⊿ABC中，∠C=90°，⊙O分别切AB、BC、AC于D、E、F，AD=5cm，BD=3cm，则⊿ABC的面积为______
2．如图，AB是⊙O直径，EF切⊙O于C，AD⊥EF于D，求证：AC 2 =AD·AB。
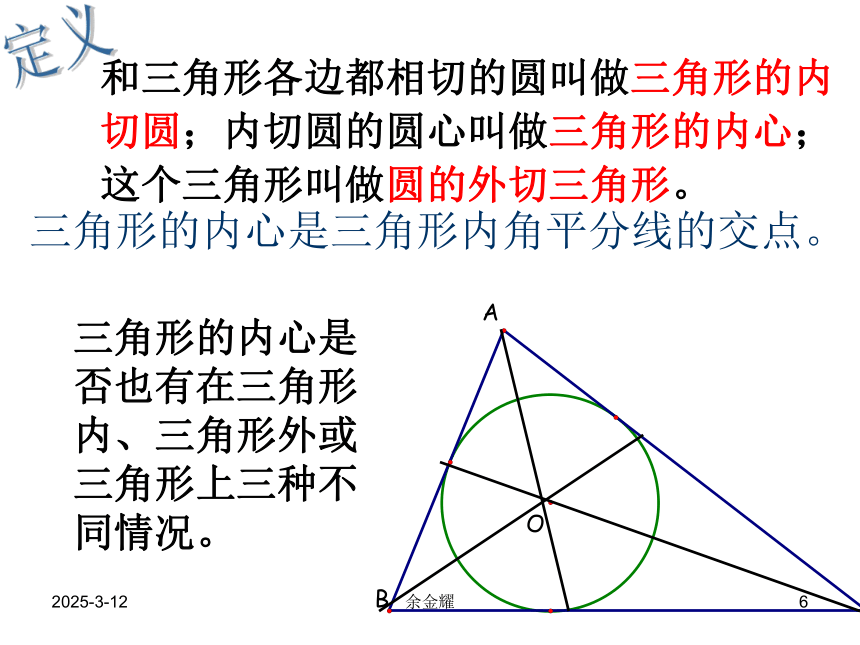
和三角形各边都相切的圆叫做三角形的内切圆；内切圆的圆心叫做三角形的内心；这个三角形叫做圆的外切三角形。
三角形的内心是三角形内角平分线的交点。
三角形的内心是否也有在三角形内、三角形外或三角形上三种不同情况。
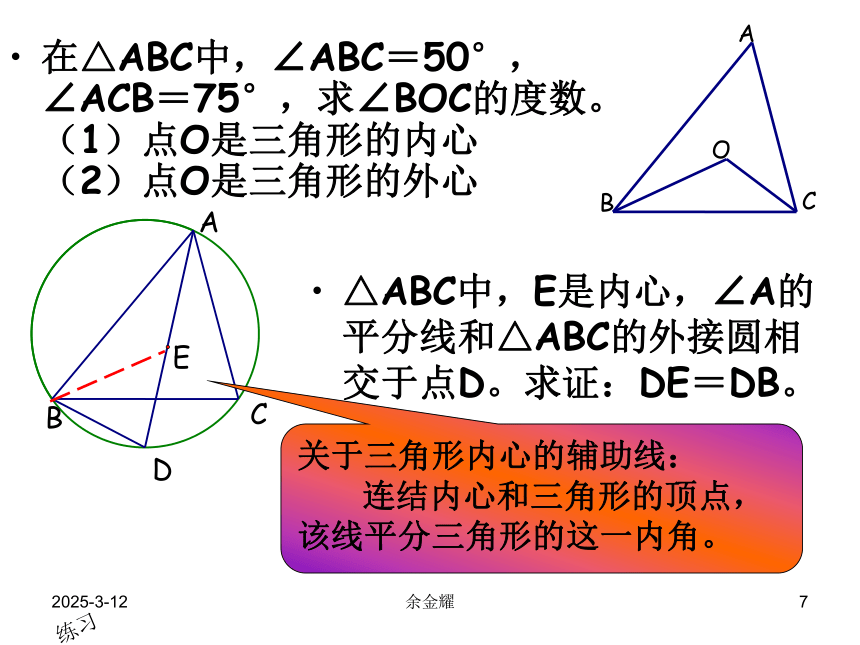
在△ABC中，∠ABC＝50°，∠ACB＝75°，求∠BOC的度数。 （1）点O是三角形的内心 （2）点O是三角形的外心
△ABC中，E是内心，∠A的平分线和△ABC的外接圆相交于点D。求证：DE＝DB。
A
B
C
O
D
A
B
C
E
练习
关于三角形内心的辅助线： 连结内心和三角形的顶点，该线平分三角形的这一内角。
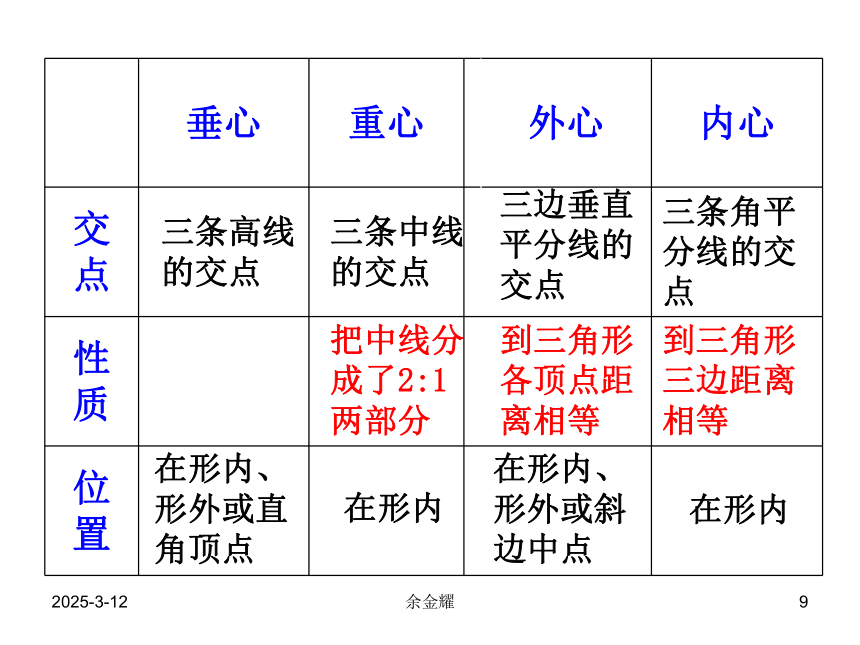
垂心 重心 外心 内心
交点
性质
位置
三条高线的交点
三条角平分线的交点
三边垂直平分线的交点
三条中线的交点
在形内、形外或直角顶点
在形内、形外或斜边中点
在形内
在形内
到三角形各顶点距离相等
到三角形三边距离相等
把中线分成了2:1两部分
A
B
C
O
三角形的外接圆：
三角形的内切圆：
A
B
C
I
O
I
特殊三角形外接圆、内切圆半径的求法：
R= —
c
2
r = ————
a+b-c
2
A
B
C
a
b
c
直角三角形外接圆、内切圆半径的求法
等边三角形外接圆、 内切圆半径的求法
基本思路：
构造三角形BOD，BO为外接圆半径，DO为内切圆半径。
A
B
C
O
D
R
r
【例2】如图8-2-7，在△ABC中，AC=BC，E是内心，AE的延长线交△ABC的外接圆于D，
求证：
(1)BE=AE
(2)AB/AC=AE/DE
3.三角形的内切圆
(1)三角形的内切圆：和三角形各边都相切的圆.
(2)三角形内心：内切圆的圆心.
(3)三角形内切圆的性质：
①到三角形三边的距离相等，
②圆心和三角形各顶点的连线平分这个角.
圆和圆的
位置关系
1、已知两圆内切，一个圆的半径是3，圆心距是2，那么另一个圆的半径是( )
A.1 B.5 C.2或3 D.1或5
2.已知两圆的半径分别为3 cm和4 cm，两个圆的圆心距为10 cm，则两圆的位置关系是( )
A.内切 B.相交
C.外切 D.外离
热身训练
3.两圆的半径比是5∶3，两圆外切时，圆心距是16，如果两圆为内含时，它们的圆心距d是( )
A.d＝4 B.4＜d＜20
C.d＞4 D.0＜d＜4
4.设⊙O1和⊙O2的半径分别是R和r，圆心距O1O2=5，且R、r是方程X -7x+10=0的两根，则⊙O1和⊙O2的位置关系是( )
A.内切 B.外切
C.相交 D.外离
12.如图8-4-7，施工工地的水平地面上，有三根外径都是1米的水泥管，两两相切地堆放在一起，则其最高点到地面的距离是( )
两个圆没有公共点，并且每个圆上的点都在另一个圆的外部。
两个圆没有公共点，并且每个圆上的点都在另一个圆的内部。
d>R+r
dd
R
r
O1
O2
d
R
r
O1
O2
两个圆有唯一公共点，并且除这公共点外，每个圆上的点都在另一个圆的外部。
两个圆有唯一公共点，并且除这公共点外，每个圆上的点都在另一个圆的内部。
d=R+r
d=R-r
d
R
r
O1
O2
d
R
r
O1
O2
两个圆有两个公共点。
R-rd
R
r
O1
O2
如图：r=1,求与这两圆都相切的圆 共有几个
从公共点个数看两圆位置关系
公共点个数
没有公共点
（相离）
一个公共点
（相切）
两个公共点
（相交）
外离
内含
外切
内切
两圆位置关系的数量特征
d：圆心距
R、r：两圆半径（R>r）
内含
相交
外离
R＋r外切
R－r内切
如果两圆相切，那么切点在连心线上。
相切两圆的性质
相交两圆的连心线垂直平分公共弦。
相交两圆的性质
【例3】半径分别是10 cm和17 cm的两圆相交，公共弦长为16 cm，求两圆的圆心距.