圆的复习

(共34张PPT)
r
O1
O2
r
.
O
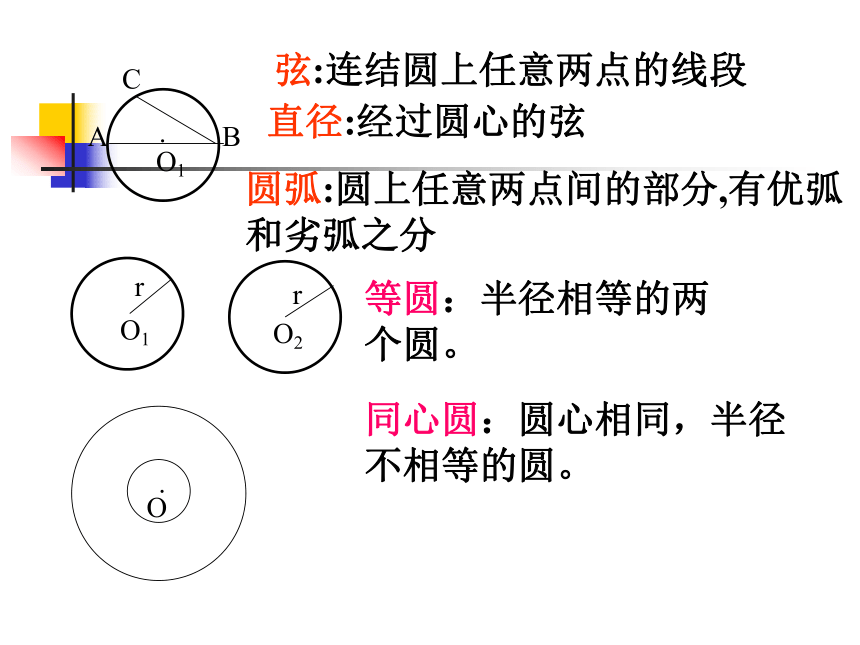
等圆：半径相等的两
个圆。
同心圆：圆心相同，半径
不相等的圆。
O1
.
A
B
C
弦:连结圆上任意两点的线段
直径:经过圆心的弦
圆弧:圆上任意两点间的部分,有优弧和劣弧之分
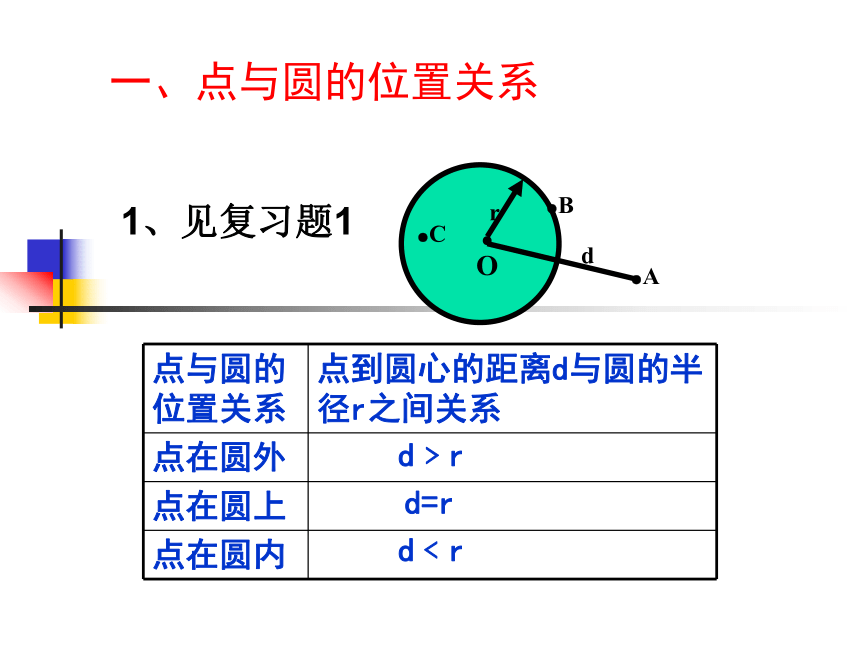
一、点与圆的位置关系
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
1、见复习题1
定理：不在同一直线上的三个点
确定一个圆。
.
.
.
A
C
B
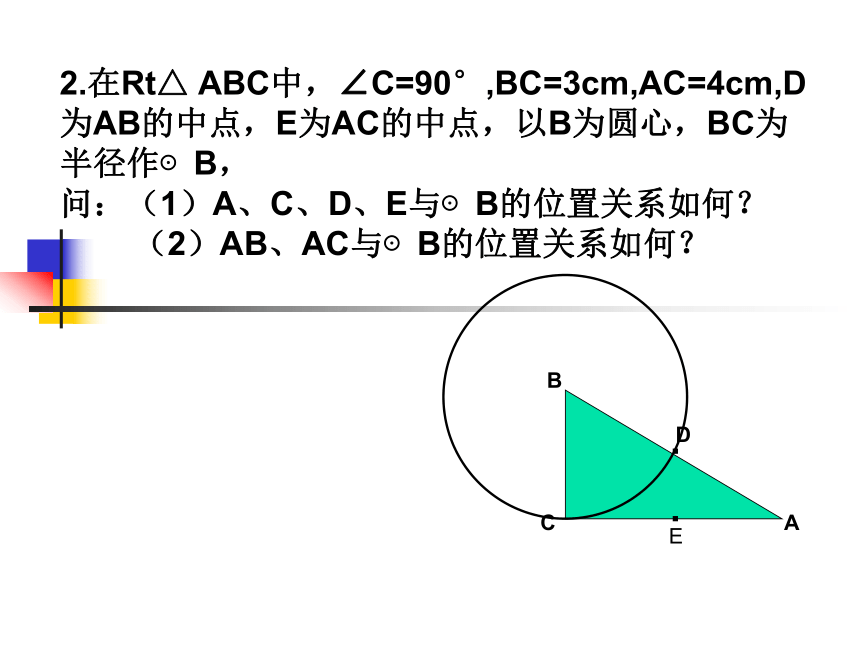
2.在Rt△ ABC中，∠C=90°,BC=3cm,AC=4cm,D为AB的中点，E为AC的中点，以B为圆心，BC为半径作⊙B，
问：（1）A、C、D、E与⊙B的位置关系如何？
（2）AB、AC与⊙B的位置关系如何？
E
D
C
A
B
·
·
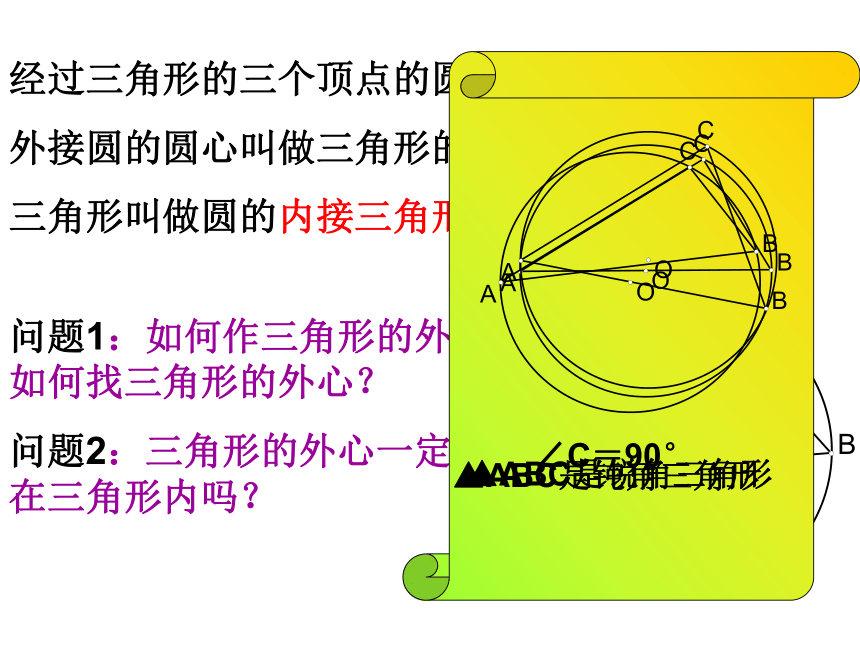
经过三角形的三个顶点的圆叫做三角形的外接圆，
外接圆的圆心叫做三角形的外心，
三角形叫做圆的内接三角形。
问题1：如何作三角形的外接圆？如何找三角形的外心？
问题2：三角形的外心一定 在三角形内吗？
∠C＝90°
▲ABC是锐角三角形
▲ABC是钝角三角形
根据这个图形，你能找到圣火台所在的位置吗？
O
二、过三点的圆及外接圆
1.过一点的圆有________个
2.过两点的圆有_________个，这些圆的圆心的都在_______________ 上.
3.过三点的圆有______________个
4.如何作过不在同一直线上的三点的圆（或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等）
5.锐角三角形的外心在三角形____，直角三角形的外心在三角形____，钝角三角形的外心在三角形____。
无数
无数
0或1
内
外
连结着两点的线段的垂直平分线
圆的轴对称性：
E
D
B
A
C
O
垂径定理：AB是直径
AB CD
CD=DB
AC=AD
CE=DE
推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧
推论2：平分弧的直径垂直平分弧所对的弦
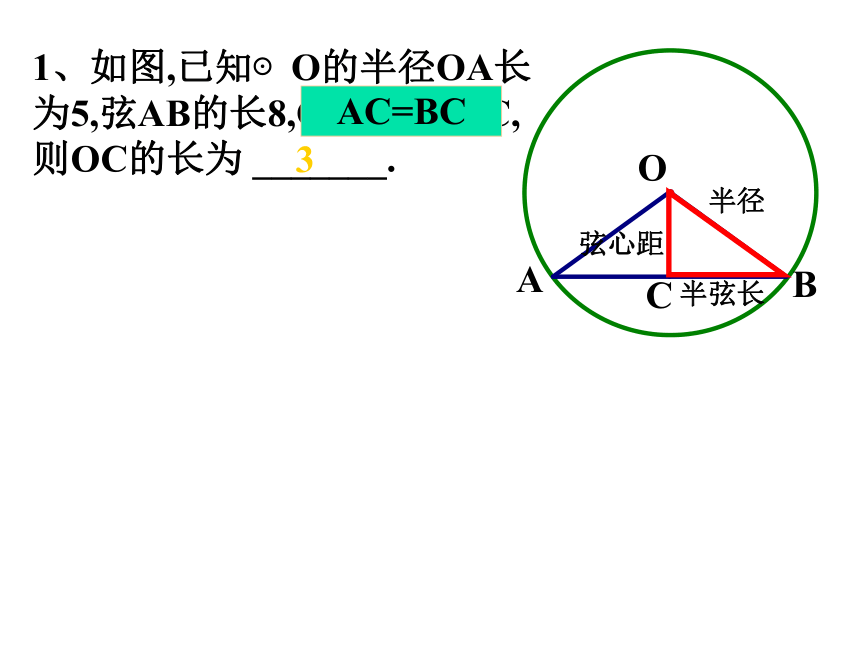
1、如图,已知⊙O的半径OA长为5,弦AB的长8,OC⊥AB于C,则OC的长为 _______.
O
A
B
C
3
AC=BC
弦心距
半径
半弦长
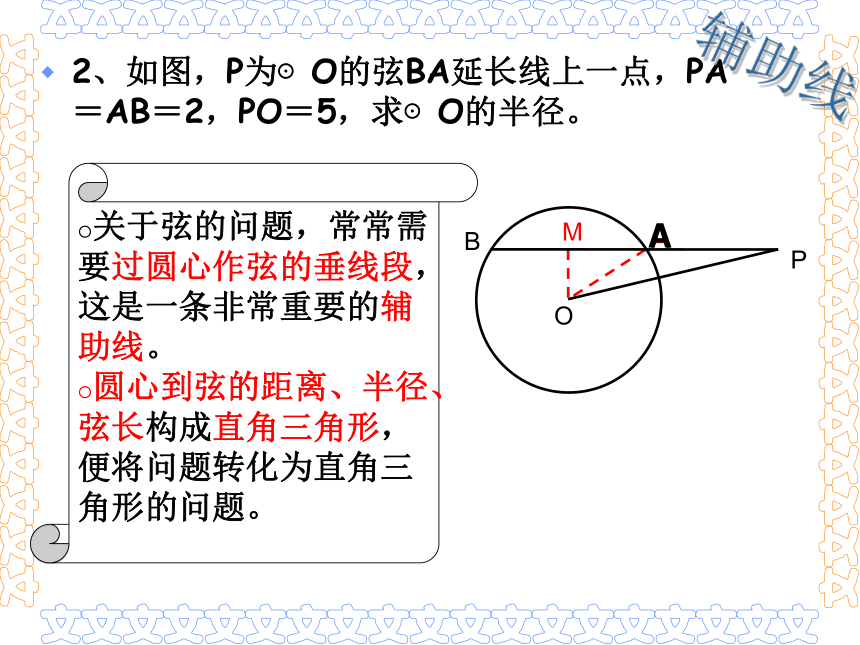
2、如图，P为⊙O的弦BA延长线上一点，PA＝AB＝2，PO＝5，求⊙O的半径。
关于弦的问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形，便将问题转化为直角三角形的问题。
M
A
P
B
O
A
O
D
C
B
A
F
E
圆心角定理：
AOB= COD
AB
=CD
AB=CD
OE=OF
（OE AB于E
OF CD于F）
圆心角定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有
一组量相等，那么它们所对应的其余各组量都分别相等。
圆周角定理： 一条弧所对的圆周角等于它所对的圆心角的一半。
A
B
C
O
推论：
半圆（或直径）所对的圆周角是直角，
90 圆周角所对的弦是直径。
同弧或等弧所对的圆周角相等；在同圆或等圆中，
相等的圆周角所对的弧也相等。
也可以理解为：一条弧所对的圆心角是它所对的圆周角的二倍；圆周角的度数等于它所对的弧的度数的一半。
图1
15
3

A
B
C
O
D
3.6
做圆的直径与找90度的圆周角也是圆里常用的辅助线
例4、半径为５的圆中，有两条平行弦AB 和CD，并且AB =６,CD=８，求AB和CD间的距离
.
E
F
.
E
F
D
A
B
C
O
(2)
A
B
D
C
(1)
O
做这类问题是，思考问题一定要全面，考虑到多种情况。
1、已知 ⊙ O中，弦AB垂直于直径CD，垂足为P，
AB=6，CP=1，则 ⊙ O的半径为 -------------- 。
2、已知 ⊙ O的直径为10cm,A是⊙ O内一点，且
OA=3cm,则 ⊙ O中过点A的最短弦长=------------- cm 。
3、两圆相交于C、B，AC=100 ，

延长AB，AC分别交
⊙ O于D、E，则 E= --------------
A
B
C
D
O
P
O
A
A
B
C
D
E
5
8
50
练习题
2、如图， ∠ABC是圆O上的三点，AB=500， ∠OBC=400，则∠OAC的度数是？
O
B
C
A
四、圆心角、弦、弧、弦心距、圆周角
前四组量中有一组量相等，其余各组量也相等；
注意：圆周角有两种情况
圆周角的推论应用广泛
2. 在⊙O中，弦AB所对的圆心角∠AOB=100°，则弦AB所对的圆周角为____________.（05年上海）
3、见复习题5、6
1.如图，⊙O为△ABC的外接圆，
AB为直径，AC=BC， 则∠A的
度数为（ ）（05泉州 ）
A.30° B.40° C.45° D.60°
500或1300
O
A
C
B
4、如图，A、B、C三点在圆上，若∠ABC=400，
则∠AOC= 。（05年大连）
6.如图，AB是⊙O的直径,BD是
⊙O的弦，延长BD到点C,使
DC=BD,连接AC交⊙O与点F.
（1）AB与AC的大小有什么关
系 为什么
（2）按角的大小分类, 请你判断
△ABC属于哪一类三角形，
并说明理由.(05宜昌)
（第20－1题）
一、圆的周长公式
二、圆的面积公式
C=2πr
S=πr2
三、弧长的计算公式
四、扇形面积计算公式
五 、大于半圆的弓形面积为
S弓形=S扇形+S△
六 、小于半圆的弓形面积为
S弓形=S扇形-S△
圆锥的侧面积和全面积
圆锥的底面周长就是其侧面展开图扇形的弧长，
圆锥的母线就是其侧面展开图扇形的半径。
1、扇形的面积是它所在圆的面积的 ，这个扇
形的圆心角的度数是_________°.
；
240°
2、 圆锥的母线为5cm，底面半径为3cm，则圆锥的表面积为_______
24πcm2
3、 扇形AOB的半径为12cm,∠AOB=120°,求扇形的面积和周长.
4、 如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.
A
例１、已知：在RtΔABC,
求以AB为轴旋转一周所得到的几何体的全面积。
分析：
以AB为轴旋转一周所得到的几何体是由公共底面的两个圆锥所组成的几何体，因此求全面积就是求两个圆锥的侧面积。
小结
已知圆锥底面半径为1cm，母线长为３cm.
（1）求它的侧面展开图的圆心角和全面积.
（2）若一甲虫从圆锥底面圆上一点
A
出发，沿
圆锥侧面绕行到母线
SA
的中点
B
，
路程是多少？
B
它所走的最短
思考题
已知AB是⊙ O的直径，弦CD与AB相交，过A，B向CD引垂线，垂足分别为E、F，求证：CE=DF。
C
A
E
B
D
F
分析：欲证CE=DF，由于C、D两点是
轴对称点，想到垂径定理，因此过O作
OM CD于M，所以CM=DM，只要证
EM=FM就行了，而AE CD，OM CD，
BF CD，由平行线等分线段定理，可得
M是E、F的中点。
O
M
5、如图，①AB是⊙O的直径，EF是⊙O的一条弦，AC⊥EF，BD⊥EF，垂足分别为C、D。
（1）求证：CE=DF
（2）若图①中的直径AB位置变成图②中的位置，则CE=DF还成立么？试说明理由。
A
B
O
C
D
E
F
M
A
B
C
D
E
F
O
M
图①
图②
变：EF是⊙O的直径，OE=5cm，弦MN=8cm，则E、F两点到直线MN的距离之和等于________
·
N
M
D
O
F
C
E
┏
┗
P
6. ⊙O的直径AB和弦CD相交于E，已知AE=6cm，EB=2cm，∠CEA=30°，求CD的长。
·
O
D
C
B
A
E
┗
F
例 4
某地有一座圆弧形的拱桥，桥下的水面宽为7.2m，拱顶高出水面2.4m，

A
B
O
7.2m
2.4m
现有一艘宽3m，船舱顶部为方形并高出水面2m的货船要经过这里。问：此货船能顺利通过这座桥吗？
r=3.9 m