圆的单元复习
图片预览



文档简介
(共17张PPT)
浙教版 数学九年级 上册 第一章
基础知识A----点与圆的位置关系
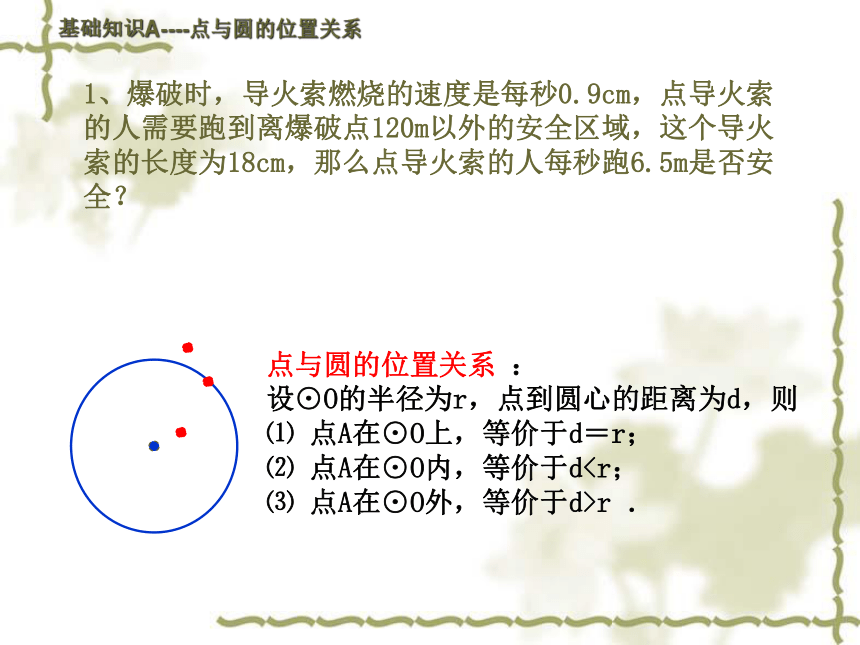
点与圆的位置关系 : 设⊙O的半径为r,点到圆心的距离为d,则 ⑴ 点A在⊙O上,等价于d=r; ⑵ 点A在⊙O内,等价于dr .
1、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,这个导火索的长度为18cm,那么点导火索的人每秒跑6.5m是否安全?
2、找圆心:有一块破损的圆面 ,你能复原,并找到它的圆心吗
基础知识B----圆的确定
圆的确定:不在同一直线上的三点可以确定一个圆。
经过三角形的三个顶点可以确定一个圆,这个圆称为三角形的外接圆。三角形是圆的内接三角形。 外接圆的圆心就是三角形三边的垂直平分线的交点。
3、O是⊿ABC的外心,∠BOC为130°,则∠A的为( )
A 115° B 65° C 50° D 115°或65°
基础知识C----圆的轴对称性
垂径定理
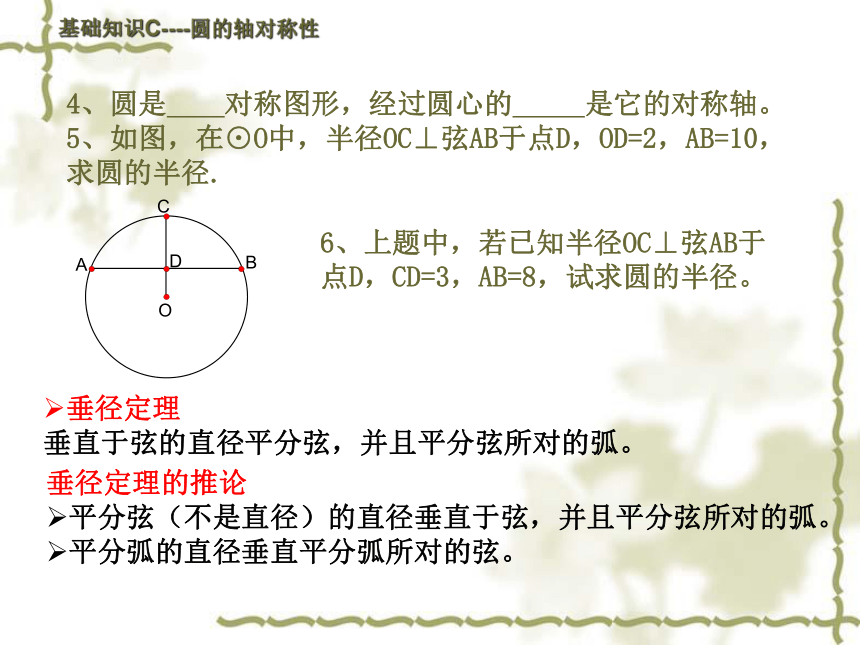
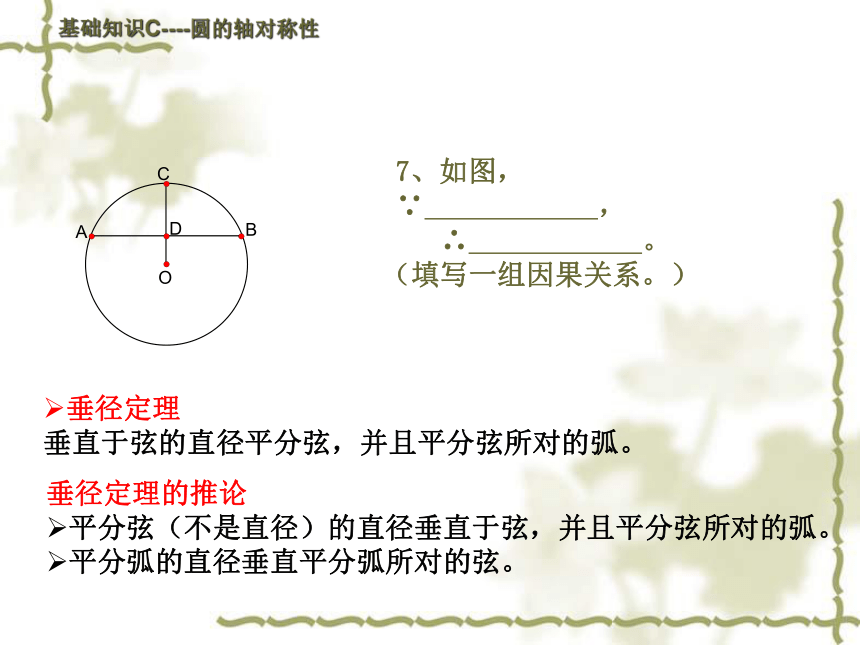
垂直于弦的直径平分弦,并且平分弦所对的弧。
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
平分弧的直径垂直平分弧所对的弦。
4、圆是 对称图形,经过圆心的 是它的对称轴。 5、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2,AB=10,求圆的半径.
6、上题中,若已知半径OC⊥弦AB于点D,CD=3,AB=8,试求圆的半径。
基础知识C----圆的轴对称性
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的弧。
7、如图,∵ ,
∴ 。
(填写一组因果关系。)
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
平分弧的直径垂直平分弧所对的弦。
基础知识D----圆心角定理
圆心角定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
8、已知:如图,在⊙O中,AB、CD为直径,则下列结论成立的有 :
⑴ AD=BC ⑵ AD∥BC ⑶ AD=BC
⌒
⌒
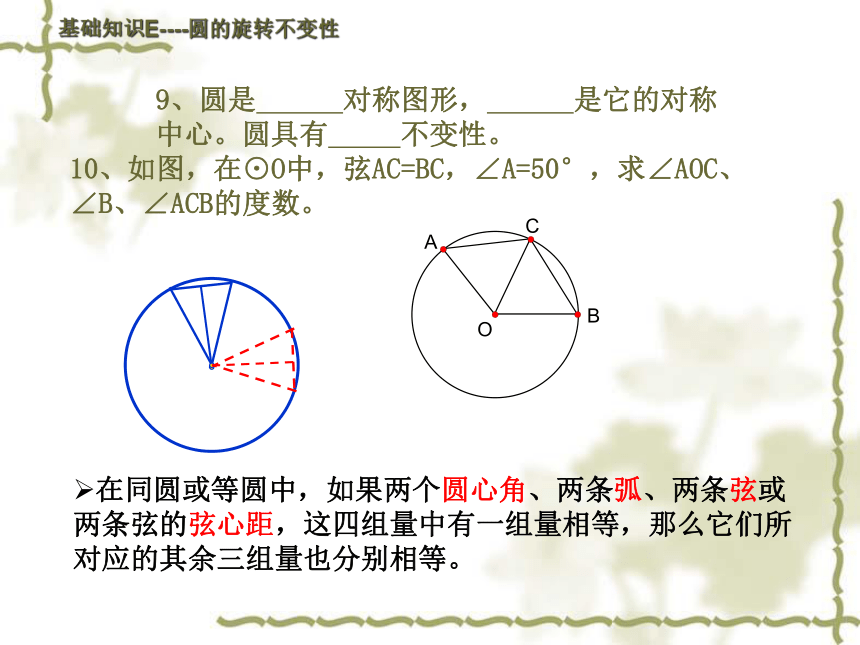
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距,这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。
基础知识E----圆的旋转不变性
9、圆是 对称图形, 是它的对称中心。圆具有 不变性。
10、如图,在⊙O中,弦AC=BC,∠A=50°,求∠AOC、∠B、∠ACB的度数。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距,这四组量中只要有一组量相等,那么它们所对应的其余三组量也分别相等。
基础知识E----圆旋转不变性
11、如图,⊙O1与⊙O2是等圆,若要说明AB=CD,你有那些方法?
基础知识F----圆周角定理
圆周角定理的推论 半圆(或直径)所对的圆周角是直角;90°的圆周角所对弦是直径。
12、如图:
⑴ 如果∠AOB=100°,则∠C= 。
⑵ 当∠C= 时,A、O、B三点在同一直线上。
O
C
A
B
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半。
O
A
B
C
E
F
D
1
2
G
基础知识----应用
13、如图, AB是半圆O的直径,C是AE的中点,CD⊥AB于D, 交AE 于F.求证:AF=CF。
⌒
基础知识G----弧、扇形
14、已知:一个扇形的半径等于一个圆的半径的2倍,且面积相等。求这个扇形的圆心角。
15、已知扇形的圆心角为135°,弧长为6πcm,则此扇形的面积为多少?
弧长计算公式:
扇形面积计算公式: 或
16、下图是由直径分别为4cm,6cm和10cm的三个半圆所组成的图形,求图中阴影部分的周长和面积。
17、已知扇形OAB的圆心角为直角,OA=4cm,以AB为直径作半圆,求圆中阴影部分的面积。
基础知识G----弧、扇形
基础知识H----圆锥的侧面积和全面积
18、圆锥的母线与底面直径都等于8cm,则圆锥的侧面积是 。
19、已知圆锥底面半径为6cm,若它的侧面积是底面积的2倍,则圆锥的母线长为 ,全面积为 。
S侧=πrl
S全=πrl+πr2
22、巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,求: ⑴ S关于X的函数表达式和自变量X的取值范围; ⑵ 画出这个函数图象,确定S的取值范围
基础知识----应用
20、下列命题中正确的为( )
A、三点确定一个圆
B、圆有且只有一个内接三角形
C、面积相等的三角形的外接圆的是等圆
D、三角形的外心是三角形任意两边的垂直平分线的交点
21、已知△ABC内接于⊙O,且AB=AC,⊙O的半径等于6cm,O点到BC的距离为2cm,求AB的长。
23、船能从圆弧形拱桥下通过吗
已知:MN=3米,AB=7.2米,CD=2.4米,D为AB中点,且CD⊥AB交CD于点H,且仓顶高出水面为2米。
A
B
C
D
基础知识----应用
M
N
A
N
2、船能从圆弧形拱桥下通过吗
已知:MN=3米,AB=7.2米,CD=2.4米,D为AB中点,且CD⊥AB交CD于点H,且仓顶高出水面为2米。
B
M
D
H
O
C
基础知识----应用
M
N
浙教版 数学九年级 上册 第一章
基础知识A----点与圆的位置关系
点与圆的位置关系 : 设⊙O的半径为r,点到圆心的距离为d,则 ⑴ 点A在⊙O上,等价于d=r; ⑵ 点A在⊙O内,等价于d
1、爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域,这个导火索的长度为18cm,那么点导火索的人每秒跑6.5m是否安全?
2、找圆心:有一块破损的圆面 ,你能复原,并找到它的圆心吗
基础知识B----圆的确定
圆的确定:不在同一直线上的三点可以确定一个圆。
经过三角形的三个顶点可以确定一个圆,这个圆称为三角形的外接圆。三角形是圆的内接三角形。 外接圆的圆心就是三角形三边的垂直平分线的交点。
3、O是⊿ABC的外心,∠BOC为130°,则∠A的为( )
A 115° B 65° C 50° D 115°或65°
基础知识C----圆的轴对称性
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的弧。
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
平分弧的直径垂直平分弧所对的弦。
4、圆是 对称图形,经过圆心的 是它的对称轴。 5、如图,在⊙O中,半径OC⊥弦AB于点D,OD=2,AB=10,求圆的半径.
6、上题中,若已知半径OC⊥弦AB于点D,CD=3,AB=8,试求圆的半径。
基础知识C----圆的轴对称性
垂径定理
垂直于弦的直径平分弦,并且平分弦所对的弧。
7、如图,∵ ,
∴ 。
(填写一组因果关系。)
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
平分弧的直径垂直平分弧所对的弦。
基础知识D----圆心角定理
圆心角定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。
8、已知:如图,在⊙O中,AB、CD为直径,则下列结论成立的有 :
⑴ AD=BC ⑵ AD∥BC ⑶ AD=BC
⌒
⌒
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距,这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。
基础知识E----圆的旋转不变性
9、圆是 对称图形, 是它的对称中心。圆具有 不变性。
10、如图,在⊙O中,弦AC=BC,∠A=50°,求∠AOC、∠B、∠ACB的度数。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距,这四组量中只要有一组量相等,那么它们所对应的其余三组量也分别相等。
基础知识E----圆旋转不变性
11、如图,⊙O1与⊙O2是等圆,若要说明AB=CD,你有那些方法?
基础知识F----圆周角定理
圆周角定理的推论 半圆(或直径)所对的圆周角是直角;90°的圆周角所对弦是直径。
12、如图:
⑴ 如果∠AOB=100°,则∠C= 。
⑵ 当∠C= 时,A、O、B三点在同一直线上。
O
C
A
B
圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半。
O
A
B
C
E
F
D
1
2
G
基础知识----应用
13、如图, AB是半圆O的直径,C是AE的中点,CD⊥AB于D, 交AE 于F.求证:AF=CF。
⌒
基础知识G----弧、扇形
14、已知:一个扇形的半径等于一个圆的半径的2倍,且面积相等。求这个扇形的圆心角。
15、已知扇形的圆心角为135°,弧长为6πcm,则此扇形的面积为多少?
弧长计算公式:
扇形面积计算公式: 或
16、下图是由直径分别为4cm,6cm和10cm的三个半圆所组成的图形,求图中阴影部分的周长和面积。
17、已知扇形OAB的圆心角为直角,OA=4cm,以AB为直径作半圆,求圆中阴影部分的面积。
基础知识G----弧、扇形
基础知识H----圆锥的侧面积和全面积
18、圆锥的母线与底面直径都等于8cm,则圆锥的侧面积是 。
19、已知圆锥底面半径为6cm,若它的侧面积是底面积的2倍,则圆锥的母线长为 ,全面积为 。
S侧=πrl
S全=πrl+πr2
22、巳知圆锥的轴截面周长为10cm,设腰长为x,圆锥的表面积为S,求: ⑴ S关于X的函数表达式和自变量X的取值范围; ⑵ 画出这个函数图象,确定S的取值范围
基础知识----应用
20、下列命题中正确的为( )
A、三点确定一个圆
B、圆有且只有一个内接三角形
C、面积相等的三角形的外接圆的是等圆
D、三角形的外心是三角形任意两边的垂直平分线的交点
21、已知△ABC内接于⊙O,且AB=AC,⊙O的半径等于6cm,O点到BC的距离为2cm,求AB的长。
23、船能从圆弧形拱桥下通过吗
已知:MN=3米,AB=7.2米,CD=2.4米,D为AB中点,且CD⊥AB交CD于点H,且仓顶高出水面为2米。
A
B
C
D
基础知识----应用
M
N
A
N
2、船能从圆弧形拱桥下通过吗
已知:MN=3米,AB=7.2米,CD=2.4米,D为AB中点,且CD⊥AB交CD于点H,且仓顶高出水面为2米。
B
M
D
H
O
C
基础知识----应用
M
N
同课章节目录
