2.2等腰三角形 讲义-浙教版八年级数学上册(含答案)
文档属性
| 名称 | 2.2等腰三角形 讲义-浙教版八年级数学上册(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览


文档简介
等腰三角形
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
掌握轴对称的性质,并能做出轴对称图像.
掌握等腰三角形的性质,并能根据性质求边长求角度.
掌握等腰三角形的判定方法.
掌握等边三角形的性质,并能在综合题型中利用性质进行转化.
掌握等边三角形的判定方法.
一、轴对称
1.轴对称图形:一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称
图形,该直线就是它的对称轴.
【注】轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的
对称轴不一定只有一条,也可能有两条或多条,因图形而定.
2.轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图
形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点.
【注】轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对
称的两个图形一定全等.
3.轴对称与轴对称图形的区别与联系
轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
4.轴对称、轴对称图形的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
【注】(1)若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
1.下面四个手机应用图标中是轴对称图形的是( D )
A.
B.
C.
D.
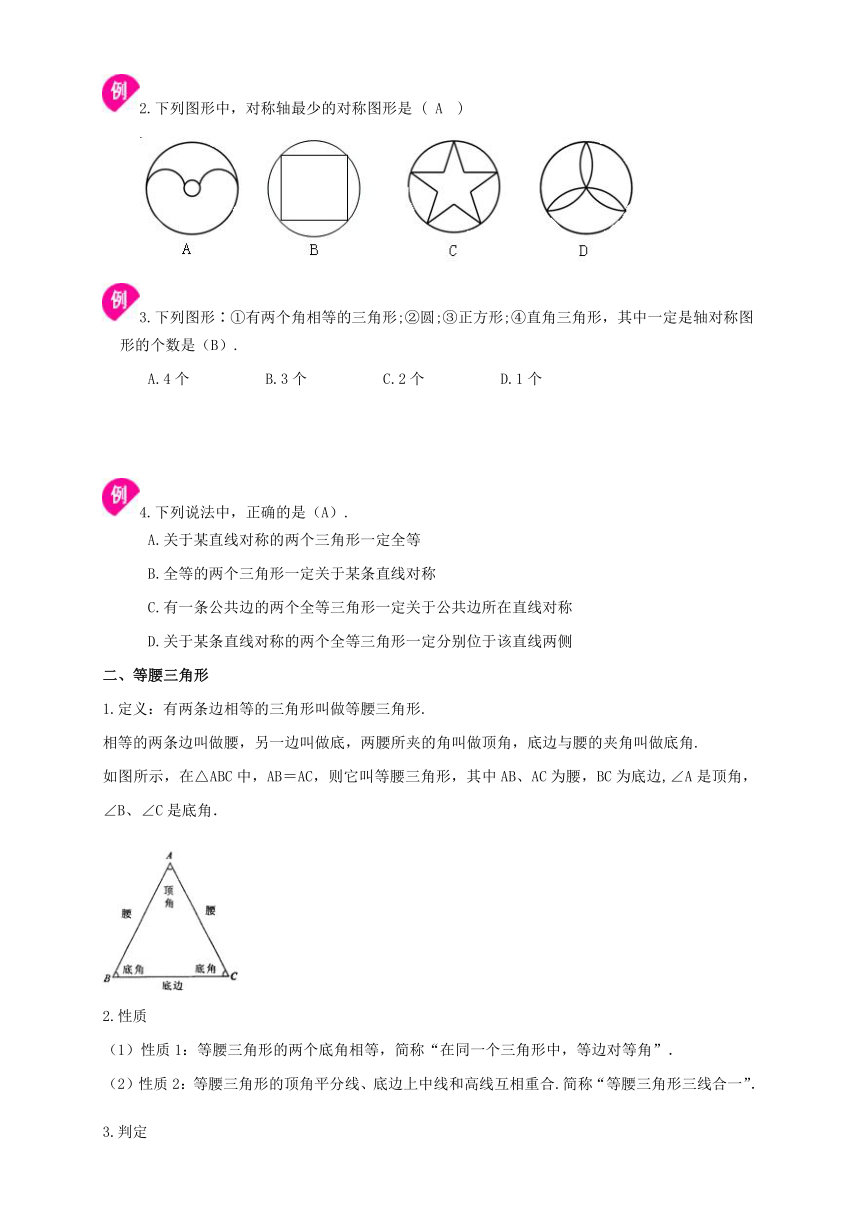
2.下列图形中,对称轴最少的对称图形是
(
A
)
3.下列图形∶①有两个角相等的三角形;②圆;③正方形;④直角三角形,其中一定是轴对称图形的个数是(B).
A.4个
B.3个
C.2个
D.1个
4.下列说法中,正确的是(A).
A.关于某直线对称的两个三角形一定全等
B.全等的两个三角形一定关于某条直线对称
C.有一条公共边的两个全等三角形一定关于公共边所在直线对称
D.关于某条直线对称的两个全等三角形一定分别位于该直线两侧
等腰三角形
1.定义:有两条边相等的三角形叫做等腰三角形.
相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,则它叫等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
2.性质
(1)性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
(2)性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
3.判定
(1)定义判定:有两条边相等的三角形是等腰三角形.
(2)判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
5.若等腰三角形的一个外角是140°,那么其底角度数为__40°或70°________.
6.等腰三角形一腰上的高与另一腰的夹角为60°,则底角的度数为___75°或15°_______.
7.等腰三角形两边长分别为3和6,则其周长为__15________.
8.等腰三角形一腰上的中线将它的周长分为9和12两部分,求腰长和底边长.
【答案】腰长为8时,底边长为5;腰长为6时,底边长为9.
9.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点D,过点D作直线EF∥BC,交AB于E,交AC于F,图中等腰三角形的个数共有(C
).
A.3个
B.4个
C.5个
D.6个
10.已知∶如图,在
△ABC中,AB=AC,BD平分∠ABC,E是底边BC的延长线上的一点且CD=
CE.
(1)求证:△BDE是等腰三角形.
(2)若∠A=36°,求∠ADE的度数.
【解析】(1)∵AB=AC,
∴∠ABC=∠ACB
∵BD平分∠ABC
∴∠ABD=∠DBC=∠ABC.
∵
CD=CE,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E=∠ACB
∴∠E=
∠DBC△BDE是等腰三角形
∵∠A=36°
∴∠ABC=∠ACB=72°
∴∠CDE=∠ACB=36°
∴∠ADE=180°-∠CDE=144°
三、等边三角形
1.定义:三边都相等的三角形叫做等边三角形.
【注】等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
2.性质:(1)等边三角形的三边都相等.
(2)等边三角形的三个内角都相等,并且每一个角都等于60°.
(3)“三线合一”.
【注】(1)等边三角形是轴对称图形,它有三条对称轴.
等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
3.判定:(1)三条边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角是60°的等腰三角形是等边三角形.
11.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是___15°或75°_______.
12.如图所示,△ABC为等边三角形,AD⊥BC,AE=AD,则∠CDE=___15°_______.
13.如图,△ABC为等边三角形,且BM=CN,AM与BN相交于点P,则∠APN=___60°____.
14.在下列结论中∶
①有一个外角是
120°的等腰三角形是等边三角形;
②有两个外角相等的等腰三角形是等边三角形;
③有一边上的高也是这边上的中线的等腰三角形是等边三角形;
④有一个角是
60°,且是轴对称的三角形是等边三角形.
其中正确的个数是(
C
).
A.4个
B.3个
C.2个
D.1个
15.如图,△ABC是等边三角形,AD是高,并且AB恰好是DE的垂直平分线,求证:△ADE是等边三角形.
【解析】∵A在DE的垂直平分线上
∴AE=AD
∴△ADE是等腰三角形
∵AB⊥DE
∴∠ADE=90°-∠BAD
∵AD⊥BD
∴∠B=90°-∠BAD
∴∠B=∠ADE=60°
∴等腰△ADE是等边三角形
1
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
掌握轴对称的性质,并能做出轴对称图像.
掌握等腰三角形的性质,并能根据性质求边长求角度.
掌握等腰三角形的判定方法.
掌握等边三角形的性质,并能在综合题型中利用性质进行转化.
掌握等边三角形的判定方法.
一、轴对称
1.轴对称图形:一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称
图形,该直线就是它的对称轴.
【注】轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的
对称轴不一定只有一条,也可能有两条或多条,因图形而定.
2.轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图
形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点.
【注】轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对
称的两个图形一定全等.
3.轴对称与轴对称图形的区别与联系
轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
4.轴对称、轴对称图形的性质
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
【注】(1)若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
(2)轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
1.下面四个手机应用图标中是轴对称图形的是( D )
A.
B.
C.
D.
2.下列图形中,对称轴最少的对称图形是
(
A
)
3.下列图形∶①有两个角相等的三角形;②圆;③正方形;④直角三角形,其中一定是轴对称图形的个数是(B).
A.4个
B.3个
C.2个
D.1个
4.下列说法中,正确的是(A).
A.关于某直线对称的两个三角形一定全等
B.全等的两个三角形一定关于某条直线对称
C.有一条公共边的两个全等三角形一定关于公共边所在直线对称
D.关于某条直线对称的两个全等三角形一定分别位于该直线两侧
等腰三角形
1.定义:有两条边相等的三角形叫做等腰三角形.
相等的两条边叫做腰,另一边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.
如图所示,在△ABC中,AB=AC,则它叫等腰三角形,其中AB、AC为腰,BC为底边,∠A是顶角,∠B、∠C是底角.
2.性质
(1)性质1:等腰三角形的两个底角相等,简称“在同一个三角形中,等边对等角”.
(2)性质2:等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”.
3.判定
(1)定义判定:有两条边相等的三角形是等腰三角形.
(2)判定定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形.可以简单的说成:在一个三角形中,等角对等边.
5.若等腰三角形的一个外角是140°,那么其底角度数为__40°或70°________.
6.等腰三角形一腰上的高与另一腰的夹角为60°,则底角的度数为___75°或15°_______.
7.等腰三角形两边长分别为3和6,则其周长为__15________.
8.等腰三角形一腰上的中线将它的周长分为9和12两部分,求腰长和底边长.
【答案】腰长为8时,底边长为5;腰长为6时,底边长为9.
9.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点D,过点D作直线EF∥BC,交AB于E,交AC于F,图中等腰三角形的个数共有(C
).
A.3个
B.4个
C.5个
D.6个
10.已知∶如图,在
△ABC中,AB=AC,BD平分∠ABC,E是底边BC的延长线上的一点且CD=
CE.
(1)求证:△BDE是等腰三角形.
(2)若∠A=36°,求∠ADE的度数.
【解析】(1)∵AB=AC,
∴∠ABC=∠ACB
∵BD平分∠ABC
∴∠ABD=∠DBC=∠ABC.
∵
CD=CE,
∴∠CDE=∠E.
∵∠ACB=∠CDE+∠E,
∴∠E=∠ACB
∴∠E=
∠DBC△BDE是等腰三角形
∵∠A=36°
∴∠ABC=∠ACB=72°
∴∠CDE=∠ACB=36°
∴∠ADE=180°-∠CDE=144°
三、等边三角形
1.定义:三边都相等的三角形叫做等边三角形.
【注】等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形.
2.性质:(1)等边三角形的三边都相等.
(2)等边三角形的三个内角都相等,并且每一个角都等于60°.
(3)“三线合一”.
【注】(1)等边三角形是轴对称图形,它有三条对称轴.
等边三角形是特殊的等腰三角形,它具有等腰三角形的一切性质.
3.判定:(1)三条边都相等的三角形是等边三角形.
(2)三个角都相等的三角形是等边三角形.
(3)有一个角是60°的等腰三角形是等边三角形.
11.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是___15°或75°_______.
12.如图所示,△ABC为等边三角形,AD⊥BC,AE=AD,则∠CDE=___15°_______.
13.如图,△ABC为等边三角形,且BM=CN,AM与BN相交于点P,则∠APN=___60°____.
14.在下列结论中∶
①有一个外角是
120°的等腰三角形是等边三角形;
②有两个外角相等的等腰三角形是等边三角形;
③有一边上的高也是这边上的中线的等腰三角形是等边三角形;
④有一个角是
60°,且是轴对称的三角形是等边三角形.
其中正确的个数是(
C
).
A.4个
B.3个
C.2个
D.1个
15.如图,△ABC是等边三角形,AD是高,并且AB恰好是DE的垂直平分线,求证:△ADE是等边三角形.
【解析】∵A在DE的垂直平分线上
∴AE=AD
∴△ADE是等腰三角形
∵AB⊥DE
∴∠ADE=90°-∠BAD
∵AD⊥BD
∴∠B=90°-∠BAD
∴∠B=∠ADE=60°
∴等腰△ADE是等边三角形
1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
