2.6直角三角形 讲义-浙教版八年级数学上册(含答案)
文档属性
| 名称 | 2.6直角三角形 讲义-浙教版八年级数学上册(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 297.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 00:00:00 | ||
图片预览



文档简介
直角三角形
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
认识直角三角形,了解直角三角形的概念.
掌握直角三角形的性质与判定.
掌握勾股定理即逆定理.
理解逆命题以及逆定理的概念.
掌握判定直角三角形全等的方法:HL.
一、直角三角形的概念
1.定义:有一个角是直角的三角形叫做直角三角形.直角三角形表示方法:Rt△.如下图,可以记作“Rt△ABC”.
2.性质
(1)在直角三角形中,两个锐角互余.
(2)在直角三角形中,斜边上的中线等于斜边的一半.
3判定
有一个角是直角的三角形是直角三角形.
有两个锐角互余的三角形是直角三角形.
勾股定理逆定理.
4.含30°角的直角三角形
在直角三角形中,如果有一个锐角为30°,那么它所对的直角边等于斜边的一半.
【注】可将两个全等的有一个角为30°的直角三角形进行拼接得出以上结论.
1.在下列条件中∶①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶2∶3,③∠A=90°-∠B,④
中,能确定△ABC是直角三角形的条件有(
D
).
A.1个
B.2个
C.3个
D.4个
2.直角三角形中,一个锐角的度数是另一个锐角的4倍,则较小锐角的度数为__18°__.
3.如图,在
△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E,如果AD=1,BC=
6,那么CE
=___4______.
4.已知OC平分∠AOB,点P为OC上-点,PD⊥OA于D,且PD=3cm,过点P作PE//OA交OB于E,∠AOB=
30°,求PE的长度__6_____cm.
5.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D.
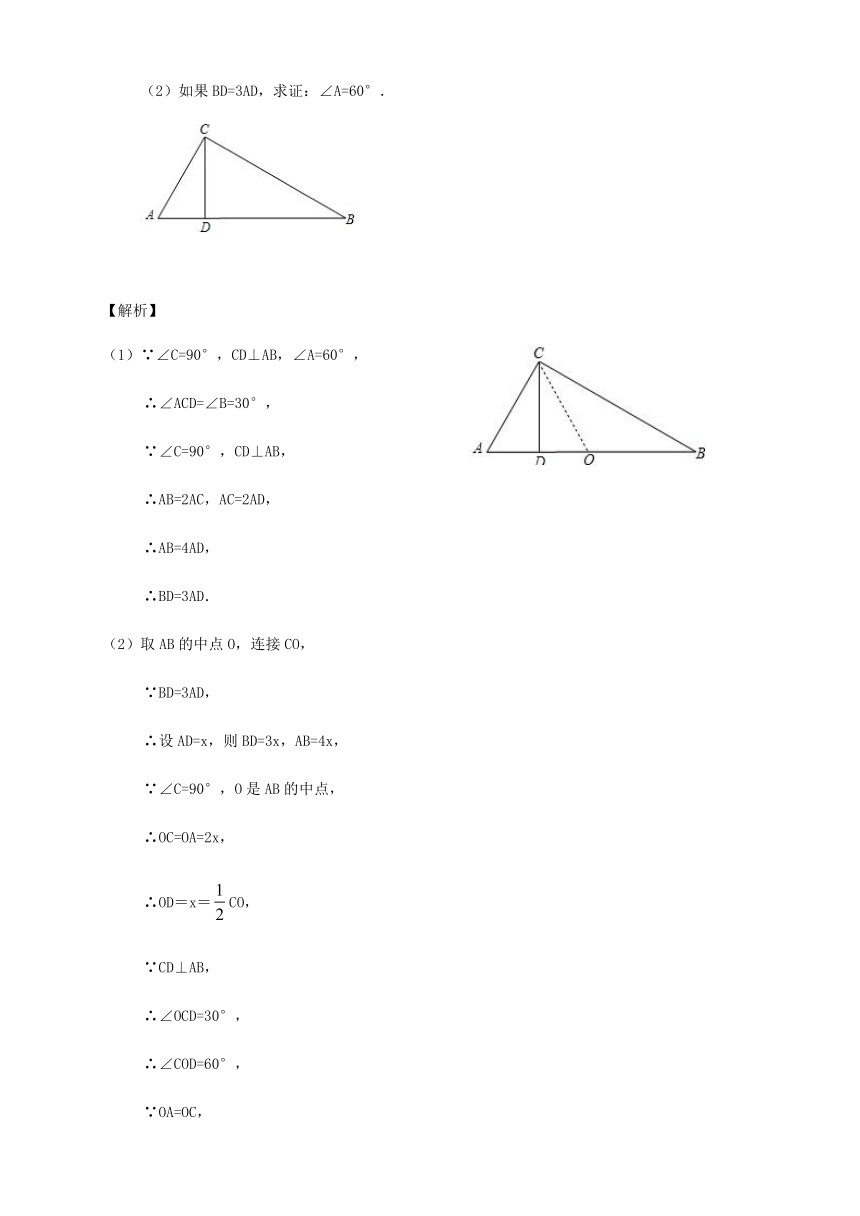
(1)如果∠A=60°,求证:BD=3AD;
(2)如果BD=3AD,求证:∠A=60°.
【解析】
(1)∵∠C=90°,CD⊥AB,∠A=60°,
∴∠ACD=∠B=30°,
∵∠C=90°,CD⊥AB,
∴AB=2AC,AC=2AD,
∴AB=4AD,
∴BD=3AD.
(2)取AB的中点O,连接CO,
∵BD=3AD,
∴设AD=x,则BD=3x,AB=4x,
∵∠C=90°,O是AB的中点,
∴OC=OA=2x,
∴OD=x=CO,
∵CD⊥AB,
∴∠OCD=30°,
∴∠COD=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴∠A=60°.
勾股定理
1.定理:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
2.勾股定理的证明
(1)邹元治的证明(“邹元治证法”).
将四个全等的直角三角形拼成如图(1)所示的正方形.
(2)赵爽的“勾股圆方图”(“赵爽弦图”).
将四个全等的直角三角形拼成如图(2)所示的正方形.
(3)美国总统加菲尔德的证明(“总统证法”).
如图(3)所示,将两个直角三角形拼成直角梯形.
6.如图,在
Rt△ABC中,∠C=90°,BC=8,AC=6,CD是斜边AB上的高,则AD的长度为______.
(第6题图)
(第7题图)
7."赵爽弦图"巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的"赵爽弦图"是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为
a,较短直角边长为
b.若ab=8,大正方形的面积为25,则小正方形的边长为___3_____.
8.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长为________.
9.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
【解析】
(1)由题意得:AC=25米,BC=7米,
AB==24(米),
答:这个梯子的顶端距地面有24米;
(2)由题意得:BA′=20米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
三、逆命题与逆定理
1.逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的
条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,则另一个命题叫做它的逆命题.
例:命题“两直线平行,同位角相等”与命题“同位角相等,两直线平行”为互逆命题.
【注】每个命题都有它的逆命题,但每个真命题的逆命题不一定是真命题.
2.逆定理
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理.这两个定理叫做互逆定
理.
10.下列说法正确的是(B).
A.命题一定是正确的
B.每一个命题都有逆命题
C.真命题的逆命题是真命题
D.每个定理都有逆定理
11.“直角三角形的两个锐角互余”,这个命题的逆命题是__有两个角互余的三角形是直角三角形__.
四、勾股定理逆定理
【探究】勾股定理的逆命题是什么?是真命题吗?
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
【证明】勾股定理的逆命题一定成立.
12.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为__36cm?_______.
五、HL判定
定理:斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
【注】这个判定方法是直角三角形所独有的,一般三角形不具备.
13.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点0.
(1)求证∶
△ABC≌△DCB.
(2)求证∶
OB=
OC.
【解析】(1)由HL定理易证Rt△ABC≌Rt△DCB
(2)由(1)全等可得∠ACB=∠DBC,即OB=OC.
1
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
认识直角三角形,了解直角三角形的概念.
掌握直角三角形的性质与判定.
掌握勾股定理即逆定理.
理解逆命题以及逆定理的概念.
掌握判定直角三角形全等的方法:HL.
一、直角三角形的概念
1.定义:有一个角是直角的三角形叫做直角三角形.直角三角形表示方法:Rt△.如下图,可以记作“Rt△ABC”.
2.性质
(1)在直角三角形中,两个锐角互余.
(2)在直角三角形中,斜边上的中线等于斜边的一半.
3判定
有一个角是直角的三角形是直角三角形.
有两个锐角互余的三角形是直角三角形.
勾股定理逆定理.
4.含30°角的直角三角形
在直角三角形中,如果有一个锐角为30°,那么它所对的直角边等于斜边的一半.
【注】可将两个全等的有一个角为30°的直角三角形进行拼接得出以上结论.
1.在下列条件中∶①∠A+∠B=∠C,②∠A∶∠B∶∠C=1∶2∶3,③∠A=90°-∠B,④
中,能确定△ABC是直角三角形的条件有(
D
).
A.1个
B.2个
C.3个
D.4个
2.直角三角形中,一个锐角的度数是另一个锐角的4倍,则较小锐角的度数为__18°__.
3.如图,在
△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E,如果AD=1,BC=
6,那么CE
=___4______.
4.已知OC平分∠AOB,点P为OC上-点,PD⊥OA于D,且PD=3cm,过点P作PE//OA交OB于E,∠AOB=
30°,求PE的长度__6_____cm.
5.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D.
(1)如果∠A=60°,求证:BD=3AD;
(2)如果BD=3AD,求证:∠A=60°.
【解析】
(1)∵∠C=90°,CD⊥AB,∠A=60°,
∴∠ACD=∠B=30°,
∵∠C=90°,CD⊥AB,
∴AB=2AC,AC=2AD,
∴AB=4AD,
∴BD=3AD.
(2)取AB的中点O,连接CO,
∵BD=3AD,
∴设AD=x,则BD=3x,AB=4x,
∵∠C=90°,O是AB的中点,
∴OC=OA=2x,
∴OD=x=CO,
∵CD⊥AB,
∴∠OCD=30°,
∴∠COD=60°,
∵OA=OC,
∴△ACO是等边三角形,
∴∠A=60°.
勾股定理
1.定理:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
2.勾股定理的证明
(1)邹元治的证明(“邹元治证法”).
将四个全等的直角三角形拼成如图(1)所示的正方形.
(2)赵爽的“勾股圆方图”(“赵爽弦图”).
将四个全等的直角三角形拼成如图(2)所示的正方形.
(3)美国总统加菲尔德的证明(“总统证法”).
如图(3)所示,将两个直角三角形拼成直角梯形.
6.如图,在
Rt△ABC中,∠C=90°,BC=8,AC=6,CD是斜边AB上的高,则AD的长度为______.
(第6题图)
(第7题图)
7."赵爽弦图"巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的"赵爽弦图"是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为
a,较短直角边长为
b.若ab=8,大正方形的面积为25,则小正方形的边长为___3_____.
8.长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长为________.
9.一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米,
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米到A′,那么梯子的底端在水平方向滑动了几米?
【解析】
(1)由题意得:AC=25米,BC=7米,
AB==24(米),
答:这个梯子的顶端距地面有24米;
(2)由题意得:BA′=20米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
三、逆命题与逆定理
1.逆命题
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的
条件,那么这两个命题叫做互逆命题.如果把其中一个命题叫做原命题,则另一个命题叫做它的逆命题.
例:命题“两直线平行,同位角相等”与命题“同位角相等,两直线平行”为互逆命题.
【注】每个命题都有它的逆命题,但每个真命题的逆命题不一定是真命题.
2.逆定理
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理.这两个定理叫做互逆定
理.
10.下列说法正确的是(B).
A.命题一定是正确的
B.每一个命题都有逆命题
C.真命题的逆命题是真命题
D.每个定理都有逆定理
11.“直角三角形的两个锐角互余”,这个命题的逆命题是__有两个角互余的三角形是直角三角形__.
四、勾股定理逆定理
【探究】勾股定理的逆命题是什么?是真命题吗?
如果三角形的三条边长,满足,那么这个三角形是直角三角形.
【证明】勾股定理的逆命题一定成立.
12.已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为__36cm?_______.
五、HL判定
定理:斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
【注】这个判定方法是直角三角形所独有的,一般三角形不具备.
13.如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点0.
(1)求证∶
△ABC≌△DCB.
(2)求证∶
OB=
OC.
【解析】(1)由HL定理易证Rt△ABC≌Rt△DCB
(2)由(1)全等可得∠ACB=∠DBC,即OB=OC.
1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
