第5章一次函数基础复习 讲义-浙教版八年级数学上册(含答案)
文档属性
| 名称 | 第5章一次函数基础复习 讲义-浙教版八年级数学上册(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 382.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 14:11:27 | ||
图片预览


文档简介
一次函数基础
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
了解常量、变量和函数的概念,了解函数的三种表示方法.
理解正比例函数和一次函数的概念,会画它们的图象.
能结合图象讨论一次函数的基本性质,能利用这些性质分析和解决问题.
一、函数的相关概念
1.变量与常量:在某一变化中,数值发生变化的量是变量,数值始终不变的量是常量.
【注】(1)“变量”是可以变化的,而“常量”是已知数;
常量与变量不是绝对的,而是对“某一变化过程”而言的,同一个量在某一个变化过
程中是常量,而在另一个变化过程中可能是变量.
2.变量与函数:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是因变量,y是x的函数.
【注】函数体现的是一个变化过程,在这一变化过程中,要着重把握以下两点:
只能有两个变量;
对于自变量x的每一个确定的值,都有唯一的函数值(y值)与之对应;
对于每一个给定的y值,x可以有一个值与之对应,也可以有多个值与之对应.
1.在圆的面积计算公式S=πr?中,变量是__S、r______,常量是__π______.
2.下列式子中,y是x的函数的有__1、2、4、6、7、8________.
3.下列函数中与表示同一函数的是(D
)
B.
C.
D.
二、函数的表示
1.函数的表示方法一共有如下三种:
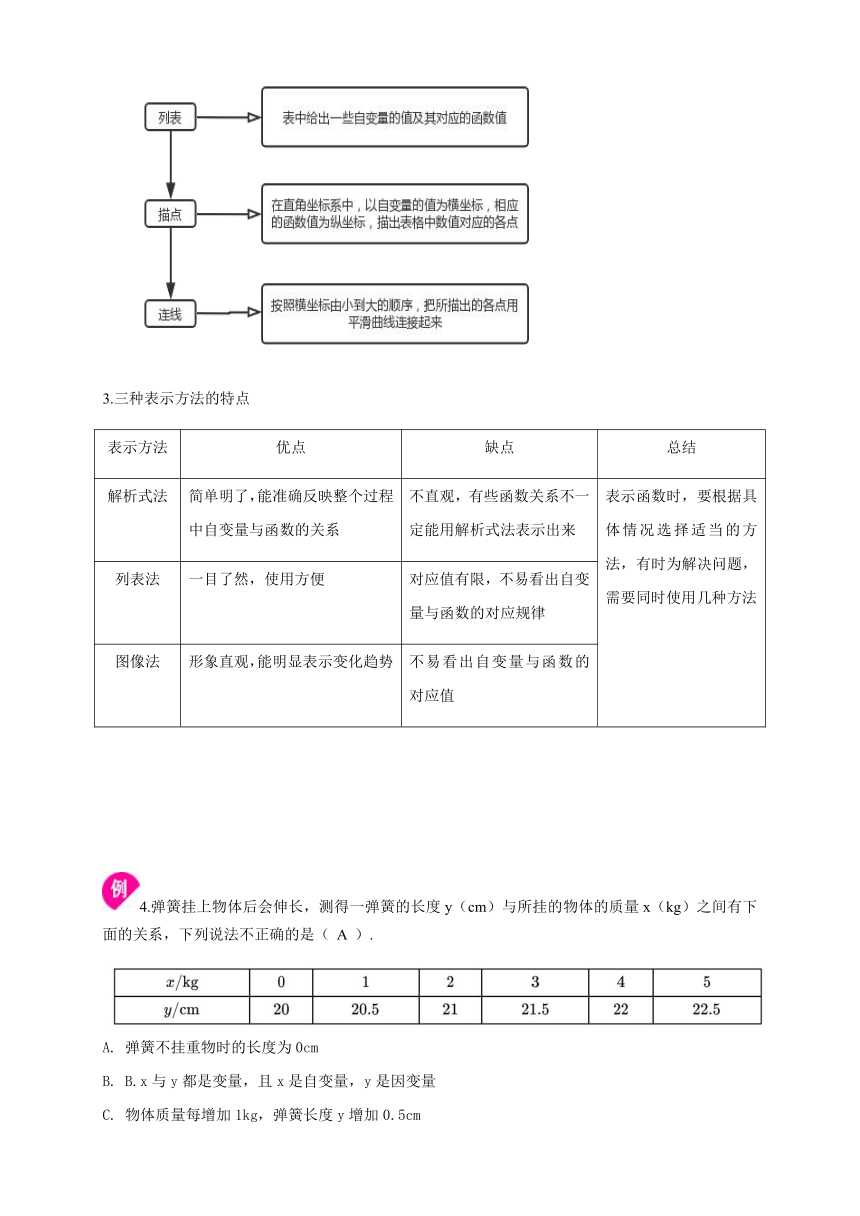
列表法:把自变量x的一系列值与函数y的对应值列成一个表的方法.
解析法:用关于自变量的数学式子表示函数与自变量之间的关系的方法,是描述函数的常用方法,这个式子叫做函数解析式.
【注】①函数关系式是等式.
②通常等式右边代数式中的变量是自变量,等式左边的一个字母表示函数.
③函数关系式在书写时有顺序性.求y与x的函数关系时,必须是只用变量x的代数式表示
y,得到的等式右边只含有x的代数式.
图像法:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么平面内由这些点组成的图像,就是这个函数的图像.
2.描点法画函数图像的一般步骤:
3.三种表示方法的特点
表示方法
优点
缺点
总结
解析式法
简单明了,能准确反映整个过程中自变量与函数的关系
不直观,有些函数关系不一定能用解析式法表示出来
表示函数时,要根据具体情况选择适当的方法,有时为解决问题,需要同时使用几种方法
列表法
一目了然,使用方便
对应值有限,不易看出自变量与函数的对应规律
图像法
形象直观,能明显表示变化趋势
不易看出自变量与函数的对应值
4.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是(
A
).
弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
物体质量每增加1kg,弹簧长度y增加0.5cm
所挂物体质量为7kg时,弹簧长度为23.5cm
5.下表是暑假旅游期间小南往家打长途电话的几次收费记录∶
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)用x表示通话时间,用y表示电话费,请写出y与x的关系式;随着x的变化,y的变化趋势是什么?
(3)你能帮小南预测一下,如果她打电话付了6元,则她大约打了多少分钟的电话?
【答案】(1)反映了时间与电话费之间的关系;时间是自变量,话费是因变量.
(2)y=0.6x,y随x增大而增大
(3)10分钟
6.从地面到高空11千米之间,气温随高度的升高而下降,每升高1千米,气温下降
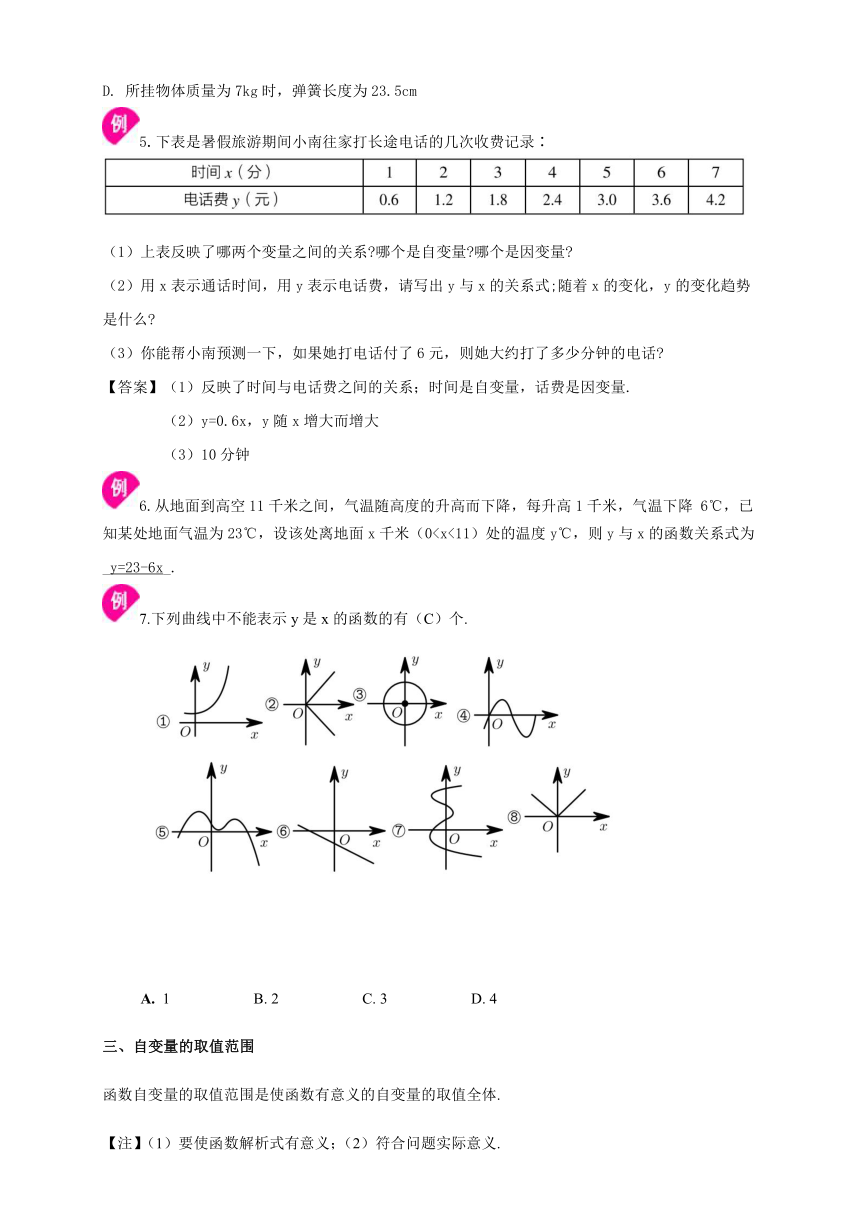
6℃,已知某处地面气温为23℃,设该处离地面x千米(07.下列曲线中不能表示y是x的函数的有(C)个.
1
B.
2
C.
3
D.
4
三、自变量的取值范围
函数自变量的取值范围是使函数有意义的自变量的取值全体.
【注】(1)要使函数解析式有意义;(2)符合问题实际意义.
函数解析式形式
整式
自变量取全体实数
分式
自变量取使分母不为0的任意实数
二次根式
自变量使被开方式为非负数
自变量出现在零指数幂或负整数指数幂的底数中
自变量为使底数不为0的实数
8.判断下列式子中y是否是x的函数,如果是,请写出自变量x的取值范围.
y=3x-5
是
(2)
是
(3)y?=x
不是
(4)y=|-3x|
是
(5)|y|=-3x
不是
(6)
是
(7)
是
(8)
是
四、一次函数
1.正比例函数与一次函数的概念
正比例函数:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数.
其中k叫做比例系数.
一次函数:一般地,形如y=kx+b(k、b是常数,k≠0)的函数,叫做一次函数.
当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
【注】(1)一次函数的解析式y=kx+b(k≠0)是一个等式,其左边是因变量y,右边是关于自变量x的整式.
(2)一次函数中自变量的次数是1,且系数不等于0.
(3)一般情况下,一次函数中自变量的取值范围是全体实数.
2.待定系数法求一次函数解析式
(1)待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
(2)用待定系数法求一次函数解析式的一般步骤
【注】对于实际问题,在求出函数解析式后,在解析式的后面需根据要求标注自变量的取值范围(未要求标注可以不标注).
9.下列函数中,哪些是一次函数__1、3______.
(1)
(2)x?-y=1
(3)y=-2x-1
(4)
(5)y=x?-x+1
10.下列说法不正确的是(C
).
A.正比例函数是一次函数的特殊形式
B.一次函数不一定是正比例函数
C.y
=kx+b是一次函数
D.2x-y=0是正比例函数
11.已知是一次函数,则m=___-3_____.
12.一次函数y=-2x+b的图像经过点(-2,3),则b=__-1____.
13.已知∶y-4与x+1成正比例,并且当x=2时,y=1.
(1)试求出y与x
的函数解析式.
(2)当y=-5时,求x的值.
【答案】(1)y=3-x
(2)x=8
五、一次函数的图像与性质
1.正比例函数的图像与性质
用描点法画函数图像
y=x,y=2x,
(2)y=-x,y=-2x,
观察上面的图像,总结正比例函数图像特点.
【总结】(1)图像:正比例函数y=kx(k是常数,k≠0)的图像是过原点(0,0)的一条直线.
我们通常过点(0,0)和点(1,k)(k是常数,k≠0)来画正比例函数图像.
(2)性质:当k>0时,图像经过一、三象限,y随x的增大而增大;
当k<0时,图像经过二、四象限,y随x的增大而减小.
2.一次函数的图像与性质
在坐标系中画出y=x,y=x+1,y=x-1的图像.
【总结】(1)图像:一次函数y=kx+b(k、b是常数,k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
我们通常过点(0,b)和点(,0)来画一次函数图像.
(2)性质:
14.正比例函数y=kx的图象经过二、四象限,则比例系数k的值可以为(A
).
A.-3
B.0
C.1
D.3
15.下列各点中,在直线y=2x-3上的是(
C
).
A.(0,3)
B.(1,1)
C.(2,1)
D.(-1,5)
16.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是(D).
A.y=-2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
17.对于函数(k是常数,k≠0)的图像,下列说法不正确的是(
C
).
A.图像是一条直线
B.图像经过点
C.经过一、三象限或二、四象限
D.y随x的增大而增大
18.已知一次函数y=kx+b,若k+b=0,则该函数的图像可能是(
A
).
1
责编:
审核:
辅导科目
数学
学生姓名
授课老师
上课课次
授课日期
班型
了解常量、变量和函数的概念,了解函数的三种表示方法.
理解正比例函数和一次函数的概念,会画它们的图象.
能结合图象讨论一次函数的基本性质,能利用这些性质分析和解决问题.
一、函数的相关概念
1.变量与常量:在某一变化中,数值发生变化的量是变量,数值始终不变的量是常量.
【注】(1)“变量”是可以变化的,而“常量”是已知数;
常量与变量不是绝对的,而是对“某一变化过程”而言的,同一个量在某一个变化过
程中是常量,而在另一个变化过程中可能是变量.
2.变量与函数:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是因变量,y是x的函数.
【注】函数体现的是一个变化过程,在这一变化过程中,要着重把握以下两点:
只能有两个变量;
对于自变量x的每一个确定的值,都有唯一的函数值(y值)与之对应;
对于每一个给定的y值,x可以有一个值与之对应,也可以有多个值与之对应.
1.在圆的面积计算公式S=πr?中,变量是__S、r______,常量是__π______.
2.下列式子中,y是x的函数的有__1、2、4、6、7、8________.
3.下列函数中与表示同一函数的是(D
)
B.
C.
D.
二、函数的表示
1.函数的表示方法一共有如下三种:
列表法:把自变量x的一系列值与函数y的对应值列成一个表的方法.
解析法:用关于自变量的数学式子表示函数与自变量之间的关系的方法,是描述函数的常用方法,这个式子叫做函数解析式.
【注】①函数关系式是等式.
②通常等式右边代数式中的变量是自变量,等式左边的一个字母表示函数.
③函数关系式在书写时有顺序性.求y与x的函数关系时,必须是只用变量x的代数式表示
y,得到的等式右边只含有x的代数式.
图像法:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么平面内由这些点组成的图像,就是这个函数的图像.
2.描点法画函数图像的一般步骤:
3.三种表示方法的特点
表示方法
优点
缺点
总结
解析式法
简单明了,能准确反映整个过程中自变量与函数的关系
不直观,有些函数关系不一定能用解析式法表示出来
表示函数时,要根据具体情况选择适当的方法,有时为解决问题,需要同时使用几种方法
列表法
一目了然,使用方便
对应值有限,不易看出自变量与函数的对应规律
图像法
形象直观,能明显表示变化趋势
不易看出自变量与函数的对应值
4.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)之间有下面的关系,下列说法不正确的是(
A
).
弹簧不挂重物时的长度为0cm
B.x与y都是变量,且x是自变量,y是因变量
物体质量每增加1kg,弹簧长度y增加0.5cm
所挂物体质量为7kg时,弹簧长度为23.5cm
5.下表是暑假旅游期间小南往家打长途电话的几次收费记录∶
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)用x表示通话时间,用y表示电话费,请写出y与x的关系式;随着x的变化,y的变化趋势是什么?
(3)你能帮小南预测一下,如果她打电话付了6元,则她大约打了多少分钟的电话?
【答案】(1)反映了时间与电话费之间的关系;时间是自变量,话费是因变量.
(2)y=0.6x,y随x增大而增大
(3)10分钟
6.从地面到高空11千米之间,气温随高度的升高而下降,每升高1千米,气温下降
6℃,已知某处地面气温为23℃,设该处离地面x千米(0
1
B.
2
C.
3
D.
4
三、自变量的取值范围
函数自变量的取值范围是使函数有意义的自变量的取值全体.
【注】(1)要使函数解析式有意义;(2)符合问题实际意义.
函数解析式形式
整式
自变量取全体实数
分式
自变量取使分母不为0的任意实数
二次根式
自变量使被开方式为非负数
自变量出现在零指数幂或负整数指数幂的底数中
自变量为使底数不为0的实数
8.判断下列式子中y是否是x的函数,如果是,请写出自变量x的取值范围.
y=3x-5
是
(2)
是
(3)y?=x
不是
(4)y=|-3x|
是
(5)|y|=-3x
不是
(6)
是
(7)
是
(8)
是
四、一次函数
1.正比例函数与一次函数的概念
正比例函数:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数.
其中k叫做比例系数.
一次函数:一般地,形如y=kx+b(k、b是常数,k≠0)的函数,叫做一次函数.
当b=0时,y=kx+b即y=kx,所以说正比例函数是一种特殊的一次函数.
【注】(1)一次函数的解析式y=kx+b(k≠0)是一个等式,其左边是因变量y,右边是关于自变量x的整式.
(2)一次函数中自变量的次数是1,且系数不等于0.
(3)一般情况下,一次函数中自变量的取值范围是全体实数.
2.待定系数法求一次函数解析式
(1)待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
(2)用待定系数法求一次函数解析式的一般步骤
【注】对于实际问题,在求出函数解析式后,在解析式的后面需根据要求标注自变量的取值范围(未要求标注可以不标注).
9.下列函数中,哪些是一次函数__1、3______.
(1)
(2)x?-y=1
(3)y=-2x-1
(4)
(5)y=x?-x+1
10.下列说法不正确的是(C
).
A.正比例函数是一次函数的特殊形式
B.一次函数不一定是正比例函数
C.y
=kx+b是一次函数
D.2x-y=0是正比例函数
11.已知是一次函数,则m=___-3_____.
12.一次函数y=-2x+b的图像经过点(-2,3),则b=__-1____.
13.已知∶y-4与x+1成正比例,并且当x=2时,y=1.
(1)试求出y与x
的函数解析式.
(2)当y=-5时,求x的值.
【答案】(1)y=3-x
(2)x=8
五、一次函数的图像与性质
1.正比例函数的图像与性质
用描点法画函数图像
y=x,y=2x,
(2)y=-x,y=-2x,
观察上面的图像,总结正比例函数图像特点.
【总结】(1)图像:正比例函数y=kx(k是常数,k≠0)的图像是过原点(0,0)的一条直线.
我们通常过点(0,0)和点(1,k)(k是常数,k≠0)来画正比例函数图像.
(2)性质:当k>0时,图像经过一、三象限,y随x的增大而增大;
当k<0时,图像经过二、四象限,y随x的增大而减小.
2.一次函数的图像与性质
在坐标系中画出y=x,y=x+1,y=x-1的图像.
【总结】(1)图像:一次函数y=kx+b(k、b是常数,k≠0)的图像也是一条直线,我们称它为直线y=kx+b.
我们通常过点(0,b)和点(,0)来画一次函数图像.
(2)性质:
14.正比例函数y=kx的图象经过二、四象限,则比例系数k的值可以为(A
).
A.-3
B.0
C.1
D.3
15.下列各点中,在直线y=2x-3上的是(
C
).
A.(0,3)
B.(1,1)
C.(2,1)
D.(-1,5)
16.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是(D).
A.y=-2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
17.对于函数(k是常数,k≠0)的图像,下列说法不正确的是(
C
).
A.图像是一条直线
B.图像经过点
C.经过一、三象限或二、四象限
D.y随x的增大而增大
18.已知一次函数y=kx+b,若k+b=0,则该函数的图像可能是(
A
).
1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
