浙教版数学九年级下册2.3三角形的内切圆课件(13张)
文档属性
| 名称 | 浙教版数学九年级下册2.3三角形的内切圆课件(13张) |
|
|
| 格式 | zip | ||
| 文件大小 | 155.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览

文档简介
(共13张PPT)
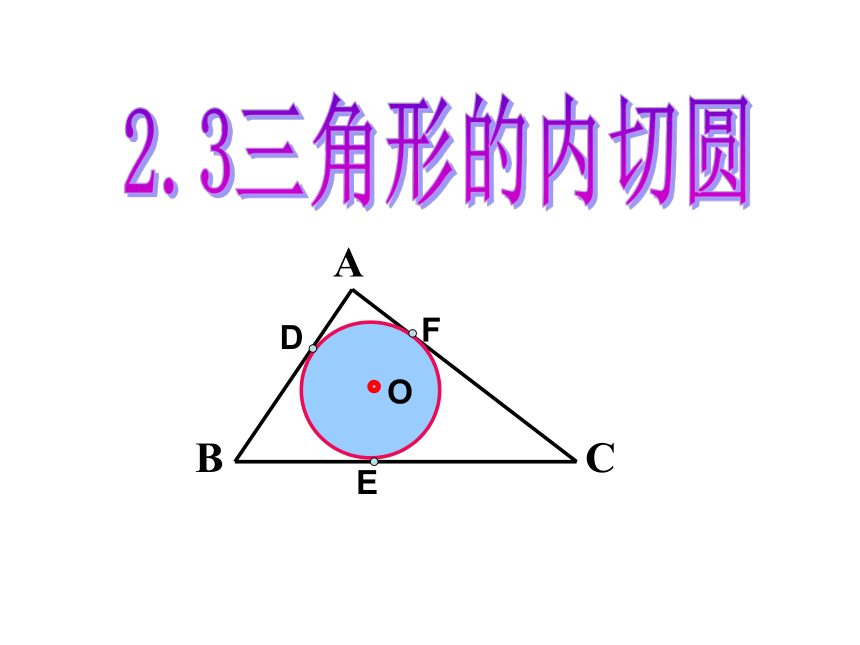
如图是一块三角形木料,木工师傅要从中裁下一个半径尽可能大的圆来做圆桌的桌面,应该怎样画出裁剪图呢?
问题
C
A
B
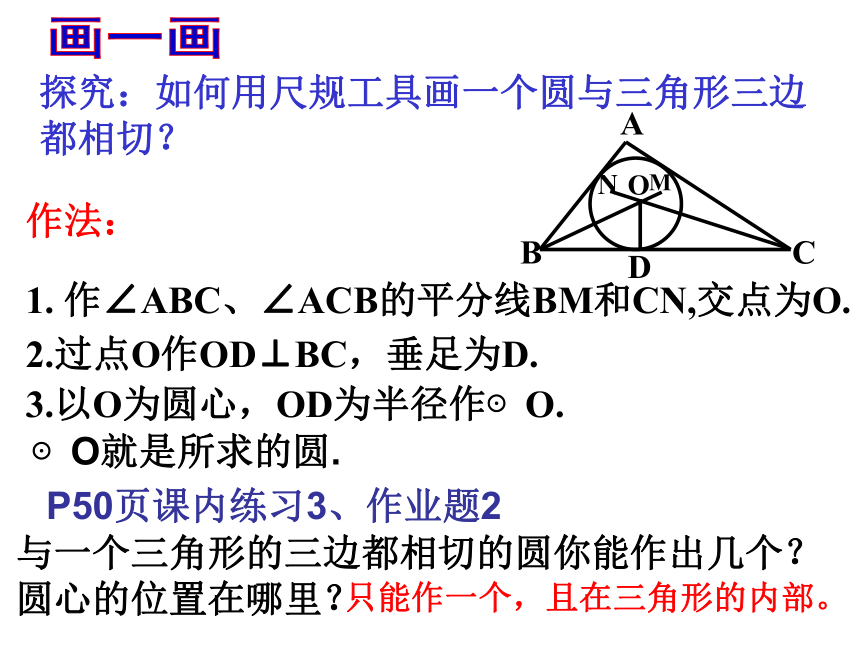
2.3三角形的内切圆
A
B
C
D
F
E
O
探究:如何用尺规工具画一个圆与三角形三边都相切?
画一画
A
B
C
M
N
O
D
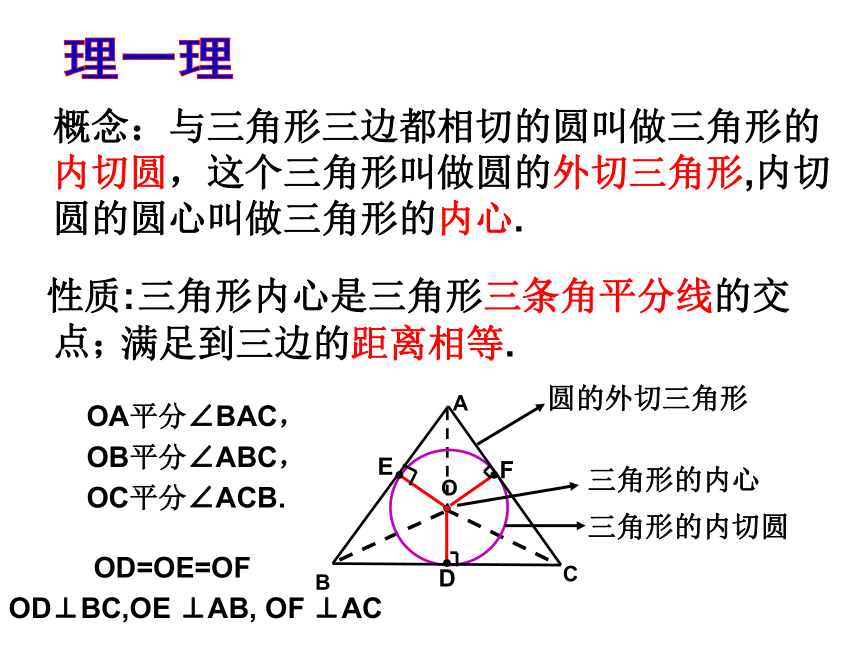
作法:
1.
作∠ABC、∠ACB的平分线BM和CN,交点为O.
2.过点O作OD⊥BC,垂足为D.
3.以O为圆心,OD为半径作⊙O.
P50页课内练习3、作业题2
与一个三角形的三边都相切的圆你能作出几个?圆心的位置在哪里?
只能作一个,且在三角形的内部。
⊙O就是所求的圆.
概念:与三角形三边都相切的圆叫做三角形的内切圆,这个三角形叫做圆的外切三角形,内切圆的圆心叫做三角形的内心.
三角形内心是三角形三条角平分线的交点;
O
A
B
C
理一理
三角形的内切圆
圆的外切三角形
三角形的内心
D
E
F
OA平分∠BAC,
OB平分∠ABC,
OC平分∠ACB.
OD=OE=OF
满足到三边的距离相等.
性质:
OD⊥BC,OE
⊥AB,
OF
⊥AC
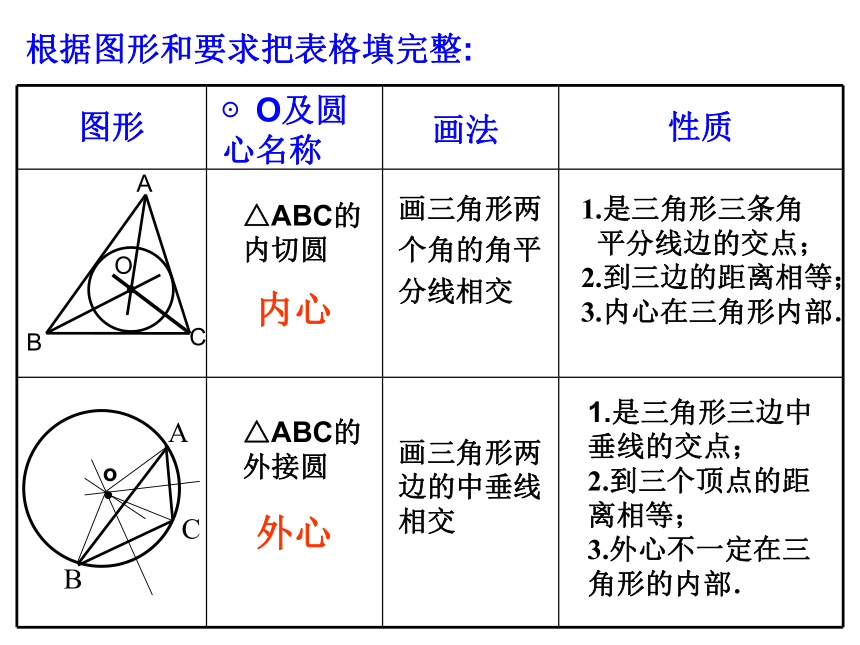
图形
性质
画三角形两边的中垂线相交
1.是三角形三边中垂线的交点;
2.到三个顶点的距离相等;
3.外心不一定在三角形的内部.
画三角形两
个角的角平
分线相交
1.是三角形三条角
平分线边的交点;
2.到三边的距离相等;
3.内心在三角形内部.
o
A
B
C
O
A
B
C
内心
外心
画法
⊙O及圆
心名称
△ABC的内切圆
△ABC的外接圆
根据图形和要求把表格填完整:
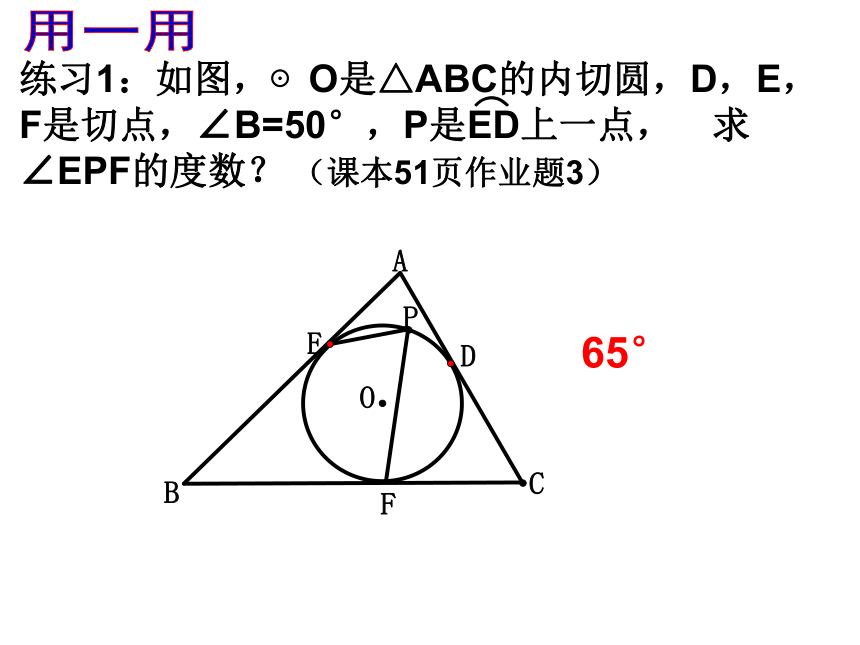
练习1:如图,⊙O是△ABC的内切圆,D,E,F是切点,∠B=50°,P是ED上一点,求∠EPF的度数?
(课本51页作业题3)
⌒
65°
用一用
练习2:如图,⊙O为RT△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=6,CD=2,求⊙O的半径?(课本51页作业题5)
1.5
练习3:已知一块等腰三角形钢板的底边长为60cm,腰长为50cm,
(1)求能从这块钢板上截得的最大圆的半径
。
(2)用一个圆完全覆盖这块钢板,这个圆的最小半径是多少?
(3)求这个等腰三角形钢板的内心与外心的距离。
(课本51页作业题6)
你能用自己的语言来表述应用三角形内心的性质解题的一般思路吗
反思
三角形内切圆的问题
三角形、四边形问题
连结内心与切点或顶点
转化
C
O
B
A
?
(1)如图,圆O是△ABC的内切圆,
拓展提升
①若∠A=80
°,则∠BOC
=
度。
②若∠BOC=100
°,则∠A
=
度。
③试探索∠BOC与∠A之间的数量关系?
②设△ABC
的内切圆的半径为r,△ABC
的各边长之和为C,△ABC
的面积S,你会有什么结论?
C
O
B
A
?
D
E
F
r
(2)如图,设△ABC的边BC=a,CA=b,AB=c,内
切圆O和各边分别相切于D,E,F,
①求证:AE=AF=1/2(a+b+c)-a;
BE=BD=1/2(a+b+c)-b;
CD=CF=1/2(a+b+c)-c.
练习:△ABC的面积12cm2,周长为24cm,则△ABC内切圆的半径为______。
拓展提升
A
B
C
O
c
D
E
r
练习:直角三角形的两直角边分别是5cm,12cm
则其内切圆的半径为______。
变式一:如图,直角三角形的两直角边分别是a,b,斜边为c
则其内切圆的半径r为___________.
(用含a、b、c的代数式表示r)
r
=
a+b-c
2
b
a
变式二:求边长为a的等边三角形内切圆半径与外接圆半径及高之比?
如图是一块三角形木料,木工师傅要从中裁下一个半径尽可能大的圆来做圆桌的桌面,应该怎样画出裁剪图呢?
问题
C
A
B
2.3三角形的内切圆
A
B
C
D
F
E
O
探究:如何用尺规工具画一个圆与三角形三边都相切?
画一画
A
B
C
M
N
O
D
作法:
1.
作∠ABC、∠ACB的平分线BM和CN,交点为O.
2.过点O作OD⊥BC,垂足为D.
3.以O为圆心,OD为半径作⊙O.
P50页课内练习3、作业题2
与一个三角形的三边都相切的圆你能作出几个?圆心的位置在哪里?
只能作一个,且在三角形的内部。
⊙O就是所求的圆.
概念:与三角形三边都相切的圆叫做三角形的内切圆,这个三角形叫做圆的外切三角形,内切圆的圆心叫做三角形的内心.
三角形内心是三角形三条角平分线的交点;
O
A
B
C
理一理
三角形的内切圆
圆的外切三角形
三角形的内心
D
E
F
OA平分∠BAC,
OB平分∠ABC,
OC平分∠ACB.
OD=OE=OF
满足到三边的距离相等.
性质:
OD⊥BC,OE
⊥AB,
OF
⊥AC
图形
性质
画三角形两边的中垂线相交
1.是三角形三边中垂线的交点;
2.到三个顶点的距离相等;
3.外心不一定在三角形的内部.
画三角形两
个角的角平
分线相交
1.是三角形三条角
平分线边的交点;
2.到三边的距离相等;
3.内心在三角形内部.
o
A
B
C
O
A
B
C
内心
外心
画法
⊙O及圆
心名称
△ABC的内切圆
△ABC的外接圆
根据图形和要求把表格填完整:
练习1:如图,⊙O是△ABC的内切圆,D,E,F是切点,∠B=50°,P是ED上一点,求∠EPF的度数?
(课本51页作业题3)
⌒
65°
用一用
练习2:如图,⊙O为RT△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=6,CD=2,求⊙O的半径?(课本51页作业题5)
1.5
练习3:已知一块等腰三角形钢板的底边长为60cm,腰长为50cm,
(1)求能从这块钢板上截得的最大圆的半径
。
(2)用一个圆完全覆盖这块钢板,这个圆的最小半径是多少?
(3)求这个等腰三角形钢板的内心与外心的距离。
(课本51页作业题6)
你能用自己的语言来表述应用三角形内心的性质解题的一般思路吗
反思
三角形内切圆的问题
三角形、四边形问题
连结内心与切点或顶点
转化
C
O
B
A
?
(1)如图,圆O是△ABC的内切圆,
拓展提升
①若∠A=80
°,则∠BOC
=
度。
②若∠BOC=100
°,则∠A
=
度。
③试探索∠BOC与∠A之间的数量关系?
②设△ABC
的内切圆的半径为r,△ABC
的各边长之和为C,△ABC
的面积S,你会有什么结论?
C
O
B
A
?
D
E
F
r
(2)如图,设△ABC的边BC=a,CA=b,AB=c,内
切圆O和各边分别相切于D,E,F,
①求证:AE=AF=1/2(a+b+c)-a;
BE=BD=1/2(a+b+c)-b;
CD=CF=1/2(a+b+c)-c.
练习:△ABC的面积12cm2,周长为24cm,则△ABC内切圆的半径为______。
拓展提升
A
B
C
O
c
D
E
r
练习:直角三角形的两直角边分别是5cm,12cm
则其内切圆的半径为______。
变式一:如图,直角三角形的两直角边分别是a,b,斜边为c
则其内切圆的半径r为___________.
(用含a、b、c的代数式表示r)
r
=
a+b-c
2
b
a
变式二:求边长为a的等边三角形内切圆半径与外接圆半径及高之比?
