浙教版九年级数学上册 第一章 二次函数 单元检测试题(Word版 含解析)
文档属性
| 名称 | 浙教版九年级数学上册 第一章 二次函数 单元检测试题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 21:55:57 | ||
图片预览



文档简介
第一章
二次函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列函数是二次函数的是?
?
?
?
A.
B.
C.
D.
?
2.
在半径为的圆中,挖去一个边长为的正方形,剩下部分面积为,则关于与之间函数关系式为(
)
A.
B.
C.
D.
?
3.
抛物线的开口方向是(?
?
?
?
?)
A.向上
B.向下
C.向左
D.向右
?
4.
喜迎圣诞,某商店销售一种进价为元/件的商品,售价为元/件,每星期可卖出件,若每件商品的售价每上涨元,则每星期就会少卖出件.设每件商品的售价上涨元(为正整数),每星期销售该商品的利润为元,则与的函数解析式为?
?
?
?
A.
B.
C.
D.
?
5.
关于二次函数,下列说法中正确的是(????????)
A.函数图象是抛物线,且开口向下
B.函数图象与轴有两个交点
C.当时,随的增大而增大
D.函数图象的顶点坐标是
?
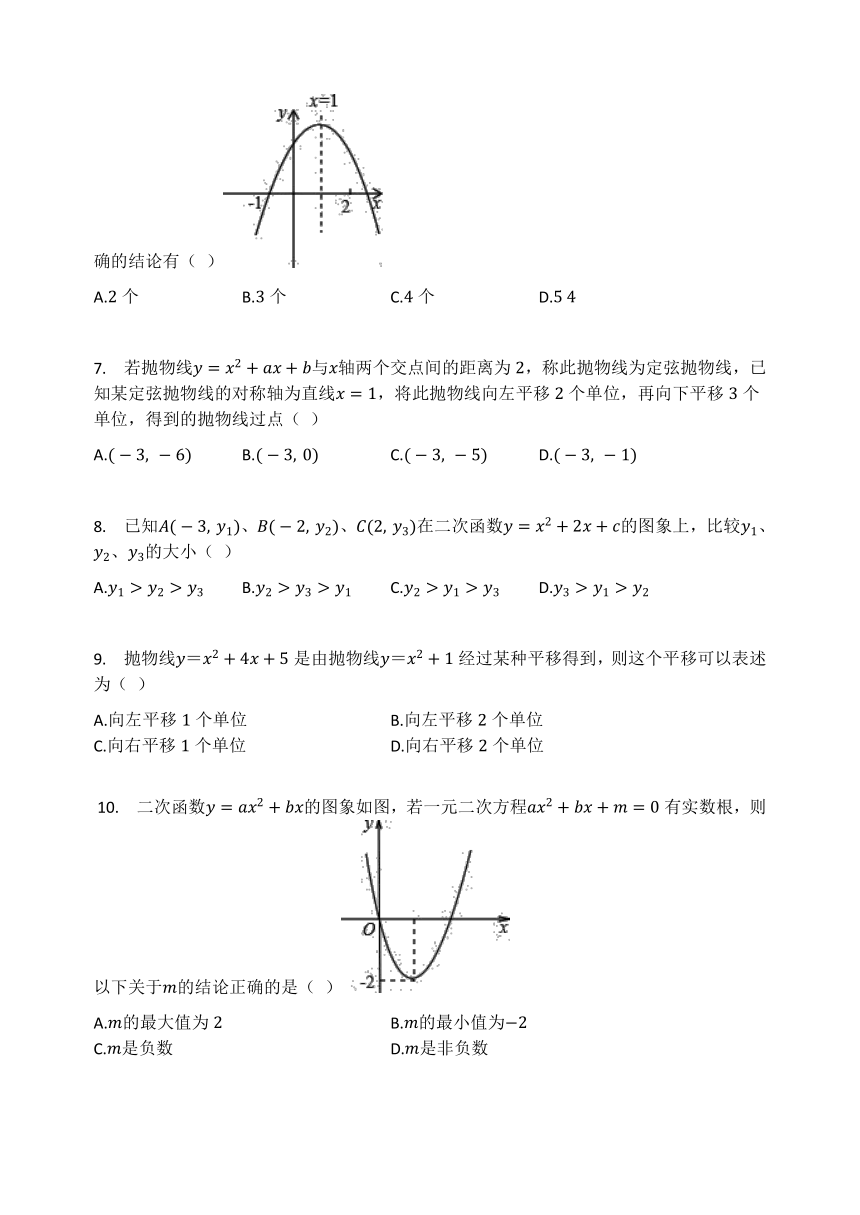
6.
已知二次函数的图象如图所示,有下列个结论:①;②;③;④;⑤(的实数),其中正确的结论有(
)
A.个
B.个
C.个
D.?
?
7.
若抛物线与轴两个交点间的距离为,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移个单位,再向下平移个单位,得到的抛物线过点(
)
A.
B.
C.
D.
?
8.
已知、、在二次函数的图象上,比较、、的大小(
)
A.
B.
C.
D.
?
9.
抛物线=是由抛物线=经过某种平移得到,则这个平移可以表述为(
)
A.向左平移个单位
B.向左平移个单位
C.向右平移个单位
D.向右平移个单位
?10.
二次函数的图象如图,若一元二次方程有实数根,则以下关于的结论正确的是(
)
A.的最大值为
B.的最小值为
C.是负数
D.是非负数
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
把抛物线一般式化为顶点式为________,顶点坐标是________.
?
12.
将二次函数的图象向下平移个单位,再向右平移个单位,得到抛物线,则________,________.
?
13.
已知二次函数的图象经过点,与轴交于,那么________.
?
14.
已知二次函数,把它改写成的形式是________.
?
15.
二次函数的图象如图所示,当函数值时,自变量的取值范围是________.
?
16.
正方形的面积与边长之间的函数关系式为________,自变量的取值范围是________.
?
17.
二次函数的图象与轴的交点坐标为________,与轴的交点坐标为________,当________时,函数值取最小值,且最小值为________.
?
18.
若抛物线=的顶点是,且经过点,则抛物线的函数关系式为________.
?
19.
已知关于的一元二次方程=的两个实数根分别为=,=,则二次函数=中,当时,的取值范围是________.
?
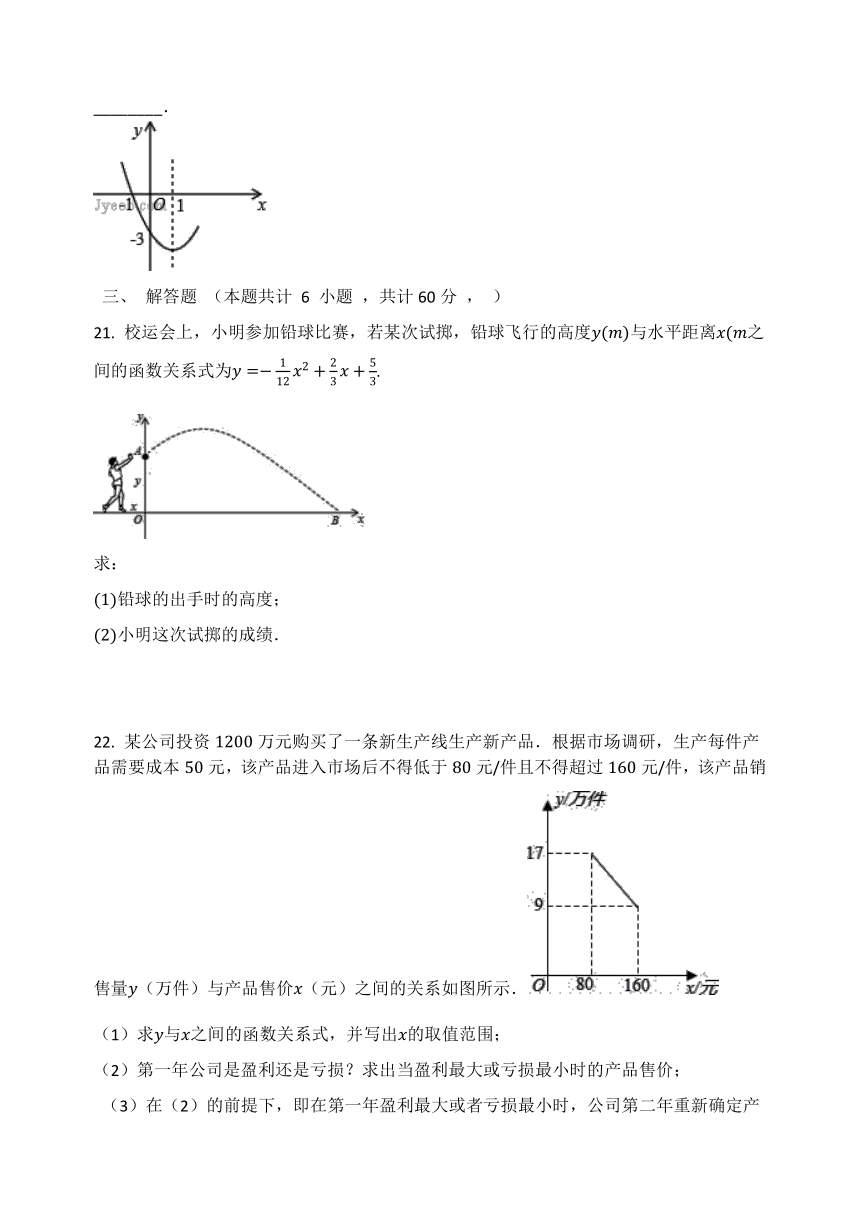
20.
已知抛物线的部分图象如图所示,当时,的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
21.
校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度与水平距离之间的函数关系式为.
求:
铅球的出手时的高度;
小明这次试掷的成绩.
?
22.
某公司投资万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本元,该产品进入市场后不得低于元/件且不得超过元/件,该产品销售量(万件)与产品售价(元)之间的关系如图所示.
(1)求与之间的函数关系式,并写出的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达万元?若能,求出第二年产品售价;若不能,说明理由.
?
23.
已知二次函数=的图象与轴交于不同的两点、,顶点为,且的面积.
(1)求的取值范围
(2)若,分别为一个两位数的十位与个位数字,求出所有这样的两位数.
?
24.
如图,有一个抛物线型拱桥,其最大高度为,跨度为,现把它的示意图放在平面直角坐标系中,求此抛物线的函数关系式.
?
25.
已知抛物线的顶点在轴上.
若点是抛物线最低点,且落在轴正半轴上,直接写出,,
的取值范围;
,是抛物线上两点,若,则;若,则,且当的绝对值为时,为等腰直角三角形(其中.
①求抛物线的解析式;
②设中点为,若,求点纵坐标的最小值.
?
26.
某商店将每件进价为元的某种商品按每件元出售,每天可售出约件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价元,每天的销售量可增加件.设商品降价元,每天销售该商品获得的利润为元.
求(元)与(元)的函数关系式,并写出的取值范围;
求当取何值时最大?并求出的最大值;
若要使每天销售利润为元,且尽可能最大的向顾客让利,应将该商品降价多少元?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:、是一次函数,故此选项错误;
、是二次函数,故此选项正确;
、分母中含有未知数不是二次函数,故此选项错误;
、,时是二次函数,故此选项错误.
故选.
2.
【答案】
B
【解答】
解:圆面积是,正方形面积是,
则函数关系式是:.
故选.
3.
【答案】
A
【解答】
解:抛物线,,
抛物线开口向上.
故选.
4.
【答案】
A
【解答】
解:设每件商品的售价上涨元(为正整数),
则每件商品的利润为:元,
总销量为:件,
商品利润为:
,
,
.
故选.
5.
【答案】
D
【解答】
解:,因为,所以函数开口向上,故错误;
,,,
故函数图象与轴无交点,故错误;
,函数开口向上,对称轴为,故当时,随的增大而减小,故错误;
,,顶点坐标为,故正确.
故选.
6.
【答案】
B
【解答】
解:①由图象可知:,,,,故此选项错误;
②当时,,即,错误;
③由对称知,当时,函数值大于,即,故此选项正确;
④当时函数值小于,,且,
即,代入得,得,故此选项正确;
⑤当时,的值最大.此时,,
而当时,,
所以,
故,即,故此选项正确.
故③④⑤正确.
故选.
7.
【答案】
B
【解答】
解:∵
某定弦抛物线的对称轴为直线,
∴
该定弦抛物线过点、,
∴
该抛物线解析式为.
将此抛物线向左平移个单位,再向下平移个单位,得到新抛物线的解析式为.
当时,,
∴
得到的新抛物线过点,
故选.
8.
【答案】
D
【解答】
解:由抛物线可知对称轴,
∵
抛物线开口向上,到对称轴的距离最近,到对称轴的距离最远,
∴
.
故选.
9.
【答案】
B
【解答】
原抛物线的顶点为,新抛物线的顶点为,
∴
是抛物线=向左平移个单位得到,
10.
【答案】
A
【解答】
解:解法一:∵
抛物线的开口向上,顶点纵坐标为,
∴
.
又∵
由图象知,即,
∵
一元二次方程有实数根,
∴
,即,即,解得,
∴
的最大值为.
解法二:一元二次方程有实数根,
可以理解为和有交点,
则,
,
故的最大值为.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
,
【解答】
解:
.
则该抛物线的顶点坐标是.
故答案是:;.
12.
【答案】
,
【解答】
解:新函数解析式为:,
∴
顶点坐标为,
∵
向右平移个单位,再向下平移个单位得到新函数解析式,
∴
原抛物线的顶点为:,
∴
原抛物线解析式为,
∴
,,
故答案是:;..
13.
【答案】
【解答】
解:把、分别代入得,
解得.
所以.
故答案为.
14.
【答案】
【解答】
解:,
故答案是.
15.
【答案】
【解答】
解:观察图象可知,函数值时,自变量的取值范围是.
故答案为:.
16.
【答案】
,
【解答】
解:正方形的面积与边长之间的函数关系式为,自变量的取值范围是.
故答案为,.
17.
【答案】
、,,,
【解答】
解:由函数
令,得
,
解得或,
∴
二次函数的图象与轴的交点坐标为:,;
令,得,
∴
函数与轴的交点坐标为,
∵
,∵
函数图象开口向上,
∴
当时,函数取得最小值为:.
18.
【答案】
=
【解答】
设抛物线的解析式为=,
将代入=得,
=,
函数解析式为=,
展开得=.
19.
【答案】
【解答】
∵
=的两个实数根分别为=,=,
∴
二次函数=与轴的两个交点坐标分别为,,
∵
=,
∴
抛物线开口向上,
∴
时,的取值范围是:.
20.
【答案】
【解答】
解:∵
函数图象与轴的一个交点横坐标为,对称轴为,
∴
函数图象与轴的另一个交点横坐标为,
由图象可知,当时,.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:当时,,
∴
铅球的出手时的高度为.
由题意可知,把代入解析式得:,
解得,(舍去),
即小明这次试掷的成绩是米.
【解答】
解:当时,,
∴
铅球的出手时的高度为.
由题意可知,把代入解析式得:,
解得,(舍去),
即小明这次试掷的成绩是米.
22.
【答案】
解:(1)设.由图象可得:,
解得:.
所以,
故的取值范围是.
(2)设该公司第一年获利万元,则
,
所以第一年公司是亏损,且当亏损最小时的产品售价为元/件.
(3)由题意可列方程,
解得:,.
两个的值都在内,
所以第二年售价是元/件或件.
【解答】
解:(1)设.由图象可得:,
解得:.
所以,
故的取值范围是.
(2)设该公司第一年获利万元,则
,
所以第一年公司是亏损,且当亏损最小时的产品售价为元/件.
(3)由题意可列方程,
解得:,.
两个的值都在内,
所以第二年售价是元/件或件.
23.
【答案】
设,,则,是方程=的两个不同的实根.
有=,=,,
∵
点的纵坐标
∴
,
即,
,
∴
;
由(1)知,=,,,.
∵
被除余数为或,
∴
被除余数也为或.
从而=,.这两个方程中符合题意的整数解有,
只有当=,=时,,
=,=,则,,,=
=,=,则,,,=
=,=,则,,,=
故所求两位数为.
【解答】
设,,则,是方程=的两个不同的实根.
有=,=,,
∵
点的纵坐标
∴
,
即,
,
∴
;
由(1)知,=,,,.
∵
被除余数为或,
∴
被除余数也为或.
从而=,.这两个方程中符合题意的整数解有,
只有当=,=时,,
=,=,则,,,=
=,=,则,,,=
=,=,则,,,=
故所求两位数为.
24.
【答案】
解:设
因为抛物线过
所以代入得:
即
故此抛物线的函数关系式为:
.
【解答】
解:设
因为抛物线过
所以代入得:
即
故此抛物线的函数关系式为:
.
25.
【答案】
解:∵
顶点是抛物线最低点,
∴
抛物线开口向上,即.
又落在轴正半轴上,
∴
,.
①∵
当时,,则;
当时,,则,
∴
抛物线的对称轴是轴,且开口向上.
又顶点在轴上,
∴
顶点是原点,
∴
抛物线的解析式为,且.
当是等腰直角三角形,时,,
又为顶点,
∴
点关于抛物线对称轴轴对称,
∵
,
∴
,
设交轴于点,则,
∴
点中一个坐标为,另一个为;
把代入,解得,
∴
抛物线的解析式为.
②设直线解析式为:,
把代入中,得
,即,
则,
∴
,
由,根据三角形中位线定理,
得中点,
根据勾股定理,,
∴
,
∵
,
∴
,
∴
,
化简得,,
根据二次函数与二次方程的关系,结合图象,
得(负根舍去),
∴
,
当时,的最小值是.
【解答】
解:∵
顶点是抛物线最低点,
∴
抛物线开口向上,即.
又落在轴正半轴上,
∴
,.
①∵
当时,,则;
当时,,则,
∴
抛物线的对称轴是轴,且开口向上.
又顶点在轴上,
∴
顶点是原点,
∴
抛物线的解析式为,且.
当是等腰直角三角形,时,,
又为顶点,
∴
点关于抛物线对称轴轴对称,
∵
,
∴
,
设交轴于点,则,
∴
点中一个坐标为,另一个为;
把代入,解得,
∴
抛物线的解析式为.
②设直线解析式为:,
把代入中,得
,即,
则,
∴
,
由,根据三角形中位线定理,
得中点,
根据勾股定理,,
∴
,
∵
,
∴
,
∴
,
化简得,,
根据二次函数与二次方程的关系,结合图象,
得(负根舍去),
∴
,
当时,的最小值是.
26.
【答案】
解:这种商品售价降低元时,所获利润为元,
则
;
由知,,开口向下,
,所以当时,取得最大值,最大值.
把代入,解得.
所以尽可能最大的向顾客让利,应将该商品降价元.
【解答】
解:这种商品售价降低元时,所获利润为元,
则
;
由知,,开口向下,
,所以当时,取得最大值,最大值.
把代入,解得.
所以尽可能最大的向顾客让利,应将该商品降价元.
二次函数
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列函数是二次函数的是?
?
?
?
A.
B.
C.
D.
?
2.
在半径为的圆中,挖去一个边长为的正方形,剩下部分面积为,则关于与之间函数关系式为(
)
A.
B.
C.
D.
?
3.
抛物线的开口方向是(?
?
?
?
?)
A.向上
B.向下
C.向左
D.向右
?
4.
喜迎圣诞,某商店销售一种进价为元/件的商品,售价为元/件,每星期可卖出件,若每件商品的售价每上涨元,则每星期就会少卖出件.设每件商品的售价上涨元(为正整数),每星期销售该商品的利润为元,则与的函数解析式为?
?
?
?
A.
B.
C.
D.
?
5.
关于二次函数,下列说法中正确的是(????????)
A.函数图象是抛物线,且开口向下
B.函数图象与轴有两个交点
C.当时,随的增大而增大
D.函数图象的顶点坐标是
?
6.
已知二次函数的图象如图所示,有下列个结论:①;②;③;④;⑤(的实数),其中正确的结论有(
)
A.个
B.个
C.个
D.?
?
7.
若抛物线与轴两个交点间的距离为,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移个单位,再向下平移个单位,得到的抛物线过点(
)
A.
B.
C.
D.
?
8.
已知、、在二次函数的图象上,比较、、的大小(
)
A.
B.
C.
D.
?
9.
抛物线=是由抛物线=经过某种平移得到,则这个平移可以表述为(
)
A.向左平移个单位
B.向左平移个单位
C.向右平移个单位
D.向右平移个单位
?10.
二次函数的图象如图,若一元二次方程有实数根,则以下关于的结论正确的是(
)
A.的最大值为
B.的最小值为
C.是负数
D.是非负数
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
把抛物线一般式化为顶点式为________,顶点坐标是________.
?
12.
将二次函数的图象向下平移个单位,再向右平移个单位,得到抛物线,则________,________.
?
13.
已知二次函数的图象经过点,与轴交于,那么________.
?
14.
已知二次函数,把它改写成的形式是________.
?
15.
二次函数的图象如图所示,当函数值时,自变量的取值范围是________.
?
16.
正方形的面积与边长之间的函数关系式为________,自变量的取值范围是________.
?
17.
二次函数的图象与轴的交点坐标为________,与轴的交点坐标为________,当________时,函数值取最小值,且最小值为________.
?
18.
若抛物线=的顶点是,且经过点,则抛物线的函数关系式为________.
?
19.
已知关于的一元二次方程=的两个实数根分别为=,=,则二次函数=中,当时,的取值范围是________.
?
20.
已知抛物线的部分图象如图所示,当时,的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
21.
校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度与水平距离之间的函数关系式为.
求:
铅球的出手时的高度;
小明这次试掷的成绩.
?
22.
某公司投资万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本元,该产品进入市场后不得低于元/件且不得超过元/件,该产品销售量(万件)与产品售价(元)之间的关系如图所示.
(1)求与之间的函数关系式,并写出的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达万元?若能,求出第二年产品售价;若不能,说明理由.
?
23.
已知二次函数=的图象与轴交于不同的两点、,顶点为,且的面积.
(1)求的取值范围
(2)若,分别为一个两位数的十位与个位数字,求出所有这样的两位数.
?
24.
如图,有一个抛物线型拱桥,其最大高度为,跨度为,现把它的示意图放在平面直角坐标系中,求此抛物线的函数关系式.
?
25.
已知抛物线的顶点在轴上.
若点是抛物线最低点,且落在轴正半轴上,直接写出,,
的取值范围;
,是抛物线上两点,若,则;若,则,且当的绝对值为时,为等腰直角三角形(其中.
①求抛物线的解析式;
②设中点为,若,求点纵坐标的最小值.
?
26.
某商店将每件进价为元的某种商品按每件元出售,每天可售出约件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价元,每天的销售量可增加件.设商品降价元,每天销售该商品获得的利润为元.
求(元)与(元)的函数关系式,并写出的取值范围;
求当取何值时最大?并求出的最大值;
若要使每天销售利润为元,且尽可能最大的向顾客让利,应将该商品降价多少元?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
【解答】
解:、是一次函数,故此选项错误;
、是二次函数,故此选项正确;
、分母中含有未知数不是二次函数,故此选项错误;
、,时是二次函数,故此选项错误.
故选.
2.
【答案】
B
【解答】
解:圆面积是,正方形面积是,
则函数关系式是:.
故选.
3.
【答案】
A
【解答】
解:抛物线,,
抛物线开口向上.
故选.
4.
【答案】
A
【解答】
解:设每件商品的售价上涨元(为正整数),
则每件商品的利润为:元,
总销量为:件,
商品利润为:
,
,
.
故选.
5.
【答案】
D
【解答】
解:,因为,所以函数开口向上,故错误;
,,,
故函数图象与轴无交点,故错误;
,函数开口向上,对称轴为,故当时,随的增大而减小,故错误;
,,顶点坐标为,故正确.
故选.
6.
【答案】
B
【解答】
解:①由图象可知:,,,,故此选项错误;
②当时,,即,错误;
③由对称知,当时,函数值大于,即,故此选项正确;
④当时函数值小于,,且,
即,代入得,得,故此选项正确;
⑤当时,的值最大.此时,,
而当时,,
所以,
故,即,故此选项正确.
故③④⑤正确.
故选.
7.
【答案】
B
【解答】
解:∵
某定弦抛物线的对称轴为直线,
∴
该定弦抛物线过点、,
∴
该抛物线解析式为.
将此抛物线向左平移个单位,再向下平移个单位,得到新抛物线的解析式为.
当时,,
∴
得到的新抛物线过点,
故选.
8.
【答案】
D
【解答】
解:由抛物线可知对称轴,
∵
抛物线开口向上,到对称轴的距离最近,到对称轴的距离最远,
∴
.
故选.
9.
【答案】
B
【解答】
原抛物线的顶点为,新抛物线的顶点为,
∴
是抛物线=向左平移个单位得到,
10.
【答案】
A
【解答】
解:解法一:∵
抛物线的开口向上,顶点纵坐标为,
∴
.
又∵
由图象知,即,
∵
一元二次方程有实数根,
∴
,即,即,解得,
∴
的最大值为.
解法二:一元二次方程有实数根,
可以理解为和有交点,
则,
,
故的最大值为.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
,
【解答】
解:
.
则该抛物线的顶点坐标是.
故答案是:;.
12.
【答案】
,
【解答】
解:新函数解析式为:,
∴
顶点坐标为,
∵
向右平移个单位,再向下平移个单位得到新函数解析式,
∴
原抛物线的顶点为:,
∴
原抛物线解析式为,
∴
,,
故答案是:;..
13.
【答案】
【解答】
解:把、分别代入得,
解得.
所以.
故答案为.
14.
【答案】
【解答】
解:,
故答案是.
15.
【答案】
【解答】
解:观察图象可知,函数值时,自变量的取值范围是.
故答案为:.
16.
【答案】
,
【解答】
解:正方形的面积与边长之间的函数关系式为,自变量的取值范围是.
故答案为,.
17.
【答案】
、,,,
【解答】
解:由函数
令,得
,
解得或,
∴
二次函数的图象与轴的交点坐标为:,;
令,得,
∴
函数与轴的交点坐标为,
∵
,∵
函数图象开口向上,
∴
当时,函数取得最小值为:.
18.
【答案】
=
【解答】
设抛物线的解析式为=,
将代入=得,
=,
函数解析式为=,
展开得=.
19.
【答案】
【解答】
∵
=的两个实数根分别为=,=,
∴
二次函数=与轴的两个交点坐标分别为,,
∵
=,
∴
抛物线开口向上,
∴
时,的取值范围是:.
20.
【答案】
【解答】
解:∵
函数图象与轴的一个交点横坐标为,对称轴为,
∴
函数图象与轴的另一个交点横坐标为,
由图象可知,当时,.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:当时,,
∴
铅球的出手时的高度为.
由题意可知,把代入解析式得:,
解得,(舍去),
即小明这次试掷的成绩是米.
【解答】
解:当时,,
∴
铅球的出手时的高度为.
由题意可知,把代入解析式得:,
解得,(舍去),
即小明这次试掷的成绩是米.
22.
【答案】
解:(1)设.由图象可得:,
解得:.
所以,
故的取值范围是.
(2)设该公司第一年获利万元,则
,
所以第一年公司是亏损,且当亏损最小时的产品售价为元/件.
(3)由题意可列方程,
解得:,.
两个的值都在内,
所以第二年售价是元/件或件.
【解答】
解:(1)设.由图象可得:,
解得:.
所以,
故的取值范围是.
(2)设该公司第一年获利万元,则
,
所以第一年公司是亏损,且当亏损最小时的产品售价为元/件.
(3)由题意可列方程,
解得:,.
两个的值都在内,
所以第二年售价是元/件或件.
23.
【答案】
设,,则,是方程=的两个不同的实根.
有=,=,,
∵
点的纵坐标
∴
,
即,
,
∴
;
由(1)知,=,,,.
∵
被除余数为或,
∴
被除余数也为或.
从而=,.这两个方程中符合题意的整数解有,
只有当=,=时,,
=,=,则,,,=
=,=,则,,,=
=,=,则,,,=
故所求两位数为.
【解答】
设,,则,是方程=的两个不同的实根.
有=,=,,
∵
点的纵坐标
∴
,
即,
,
∴
;
由(1)知,=,,,.
∵
被除余数为或,
∴
被除余数也为或.
从而=,.这两个方程中符合题意的整数解有,
只有当=,=时,,
=,=,则,,,=
=,=,则,,,=
=,=,则,,,=
故所求两位数为.
24.
【答案】
解:设
因为抛物线过
所以代入得:
即
故此抛物线的函数关系式为:
.
【解答】
解:设
因为抛物线过
所以代入得:
即
故此抛物线的函数关系式为:
.
25.
【答案】
解:∵
顶点是抛物线最低点,
∴
抛物线开口向上,即.
又落在轴正半轴上,
∴
,.
①∵
当时,,则;
当时,,则,
∴
抛物线的对称轴是轴,且开口向上.
又顶点在轴上,
∴
顶点是原点,
∴
抛物线的解析式为,且.
当是等腰直角三角形,时,,
又为顶点,
∴
点关于抛物线对称轴轴对称,
∵
,
∴
,
设交轴于点,则,
∴
点中一个坐标为,另一个为;
把代入,解得,
∴
抛物线的解析式为.
②设直线解析式为:,
把代入中,得
,即,
则,
∴
,
由,根据三角形中位线定理,
得中点,
根据勾股定理,,
∴
,
∵
,
∴
,
∴
,
化简得,,
根据二次函数与二次方程的关系,结合图象,
得(负根舍去),
∴
,
当时,的最小值是.
【解答】
解:∵
顶点是抛物线最低点,
∴
抛物线开口向上,即.
又落在轴正半轴上,
∴
,.
①∵
当时,,则;
当时,,则,
∴
抛物线的对称轴是轴,且开口向上.
又顶点在轴上,
∴
顶点是原点,
∴
抛物线的解析式为,且.
当是等腰直角三角形,时,,
又为顶点,
∴
点关于抛物线对称轴轴对称,
∵
,
∴
,
设交轴于点,则,
∴
点中一个坐标为,另一个为;
把代入,解得,
∴
抛物线的解析式为.
②设直线解析式为:,
把代入中,得
,即,
则,
∴
,
由,根据三角形中位线定理,
得中点,
根据勾股定理,,
∴
,
∵
,
∴
,
∴
,
化简得,,
根据二次函数与二次方程的关系,结合图象,
得(负根舍去),
∴
,
当时,的最小值是.
26.
【答案】
解:这种商品售价降低元时,所获利润为元,
则
;
由知,,开口向下,
,所以当时,取得最大值,最大值.
把代入,解得.
所以尽可能最大的向顾客让利,应将该商品降价元.
【解答】
解:这种商品售价降低元时,所获利润为元,
则
;
由知,,开口向下,
,所以当时,取得最大值,最大值.
把代入,解得.
所以尽可能最大的向顾客让利,应将该商品降价元.
同课章节目录
