浙教版九年级数学上册 第三章 圆的基本性质 单元检测试题(Word版 含解析)
文档属性
| 名称 | 浙教版九年级数学上册 第三章 圆的基本性质 单元检测试题(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 146.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-09 22:48:19 | ||
图片预览

文档简介
1049020010693400123190000第三章 圆的基本性质 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 如果⊙O的周长为C,那么它的半径R为( )
A.2πC B.πC C.Cπ D.C2π
?
2. 已知⊙O的半径分别是3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.无法确定
?
3. 下列四边形中,一定有外接圆的是( )
A.平行四边形 B.菱形 C.矩形 D.梯形
?
4. 如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=214,则∠AED的度数是( )
A.30? B.60? C.45? D.36?
?
5. 可以作圆,且只可以作一个圆的条件是( )
A.已知圆心 B.已知半径
C.过三个已知点 D.过不在一直线上的三点
?
6. 扇形的弧长为10πcm,面积为120πcm2,则扇形的半径是( )
A.12cm B.24cm C.28cm D.30cm
?
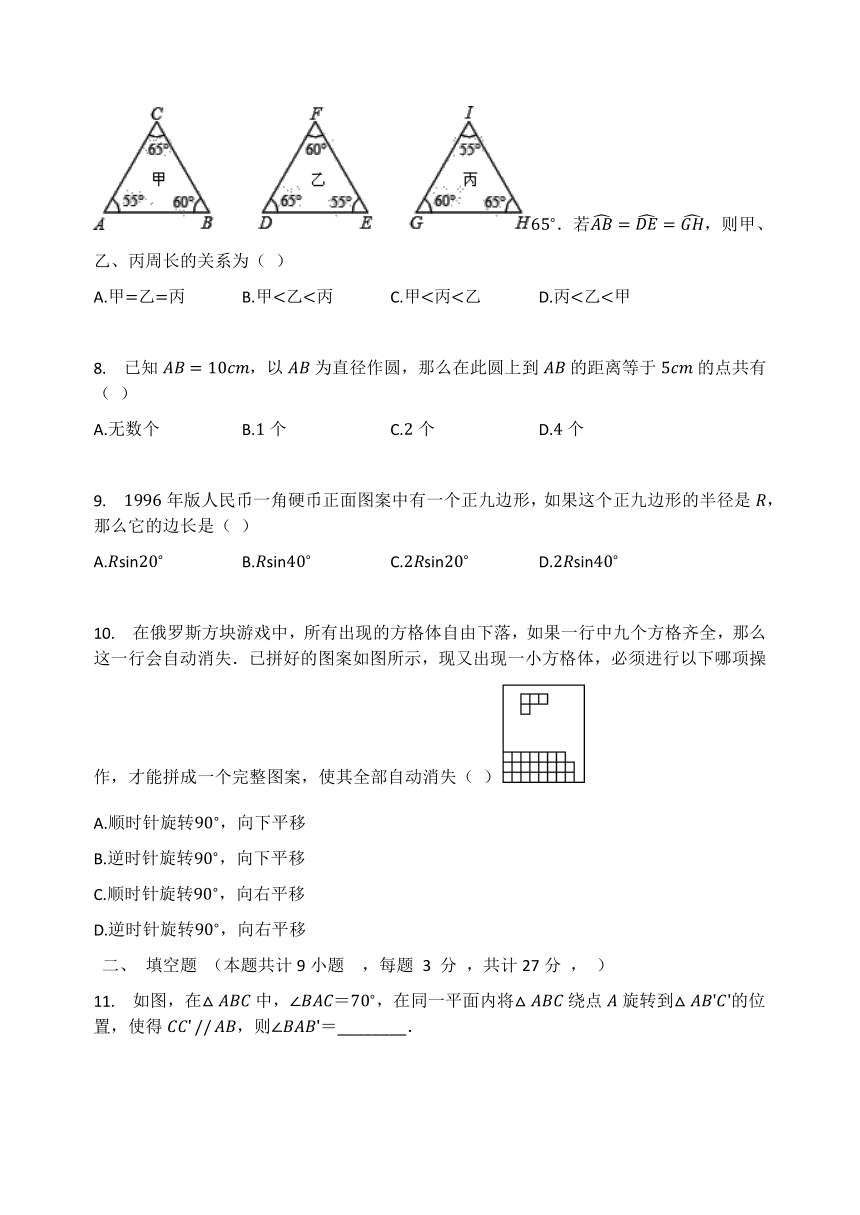
7. 如图所示,甲、乙、丙三个三角形,每个三角形的内角均为55?、60?、65?.若AB=DE=GH,则甲、乙、丙周长的关系为( )
A.甲=乙=丙 B.甲<乙<丙 C.甲<丙<乙 D.丙<乙<甲
?
8. 已知AB=10cm,以AB为直径作圆,那么在此圆上到AB的距离等于5cm的点共有( )
A.无数个 B.1个 C.2个 D.4个
?
9. 1996年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( )
A.Rsin20? B.Rsin40? C.2Rsin20? D.2Rsin40?
?
10. 在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90?,向下平移
B.逆时针旋转90?,向下平移
C.顺时针旋转90?,向右平移
D.逆时针旋转90?,向右平移
二、 填空题 (本题共计9小题 ,每题 3 分 ,共计27分 , ) ?
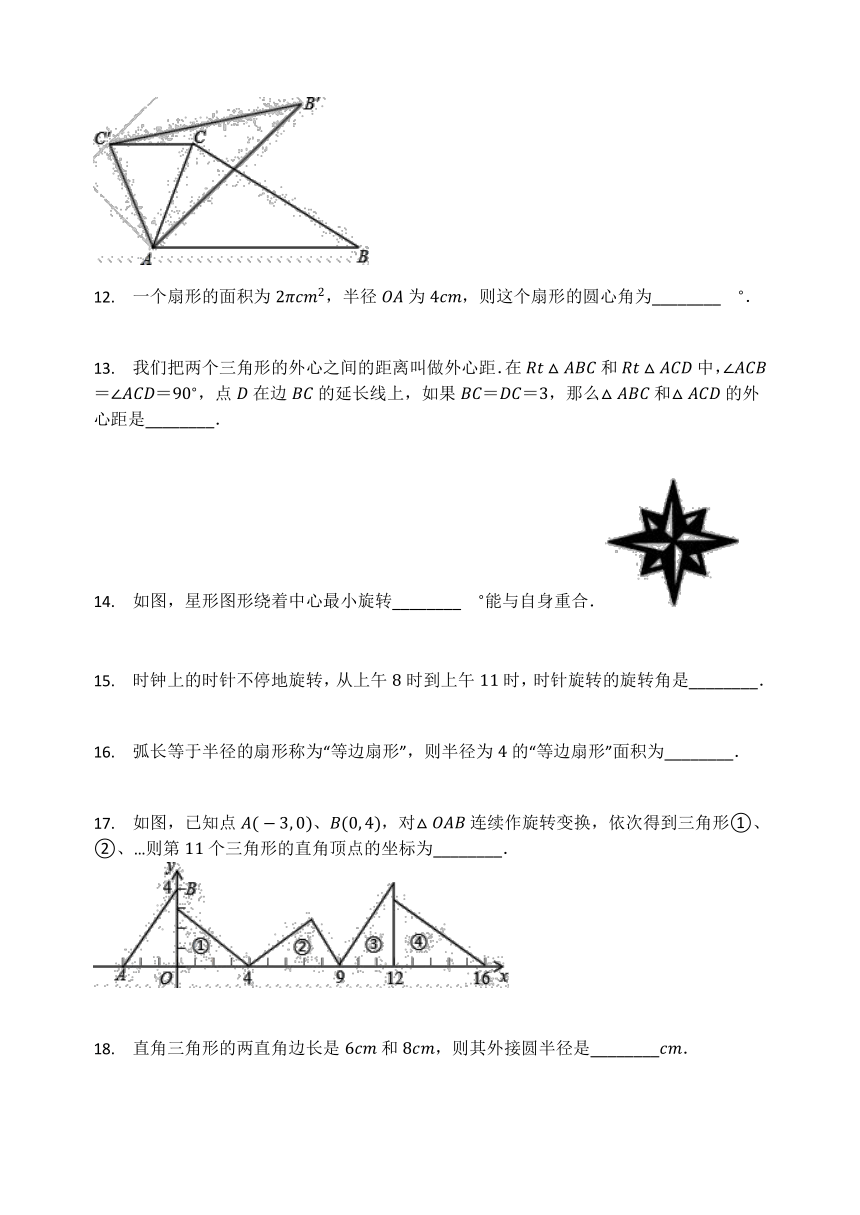
11. 如图,在△ABC中,∠BAC=70?,在同一平面内将△ABC绕点A旋转到△AB'C'的位置,使得CC'?//?AB,则∠BAB'=________.
?
12. 一个扇形的面积为2πcm2,半径OA为4cm,则这个扇形的圆心角为________??.
?
13. 我们把两个三角形的外心之间的距离叫做外心距.在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90?,点D在边BC的延长线上,如果BC=DC=3,那么△ABC和△ACD的外心距是________.
?
14. 如图,星形图形绕着中心最小旋转________??能与自身重合.
?
15. 时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是________.
?
16. 弧长等于半径的扇形称为“等边扇形”,则半径为4的“等边扇形”面积为________.
?
17. 如图,已知点A(-3,?0)、B(0,?4),对△OAB连续作旋转变换,依次得到三角形①、②、…则第11个三角形的直角顶点的坐标为________.
?
18. 直角三角形的两直角边长是6cm和8cm,则其外接圆半径是________cm.
?
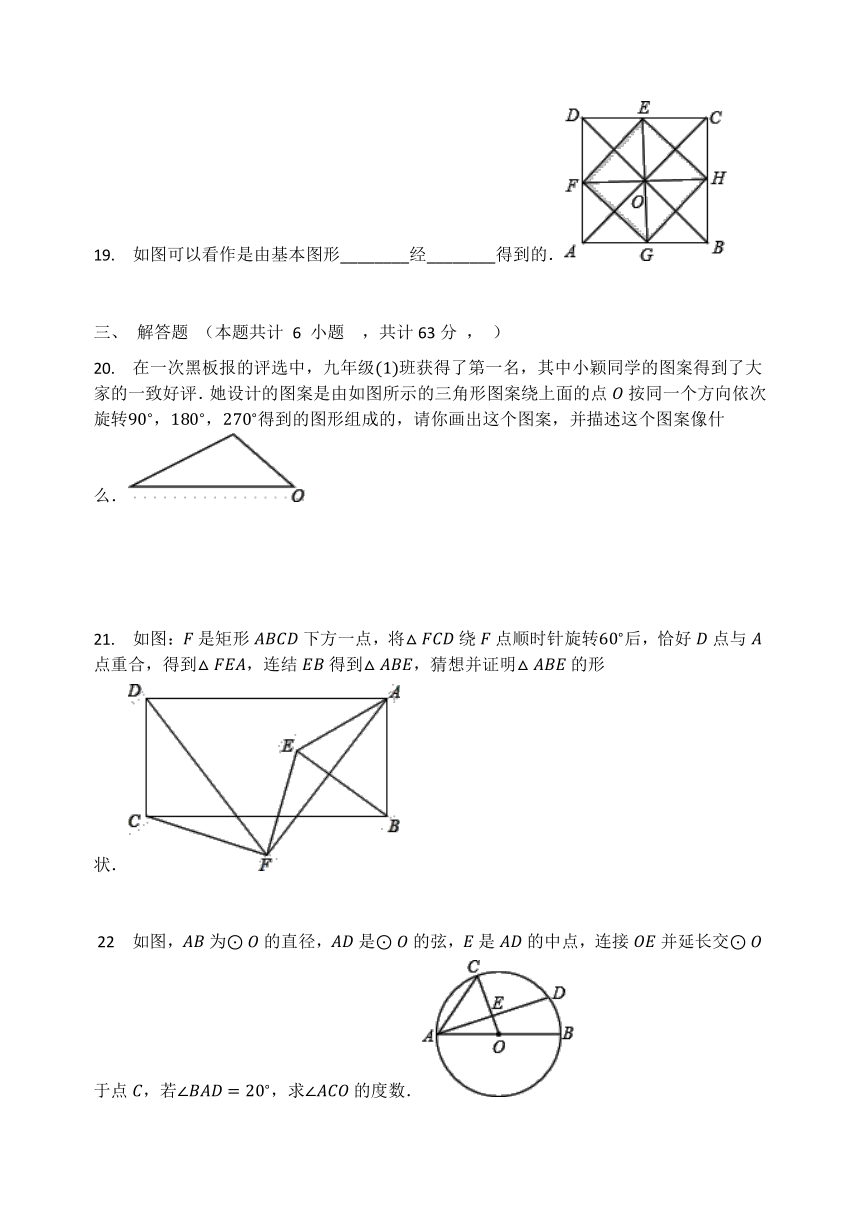
19. 如图可以看作是由基本图形________经________得到的.
?
三、 解答题 (本题共计 6 小题 ,共计63分 , ) ?
20. 在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90?,180?,270?得到的图形组成的,请你画出这个图案,并描述这个图案像什么.
?
21. 如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60?后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
?22 如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20?,求∠ACO的度数.
?
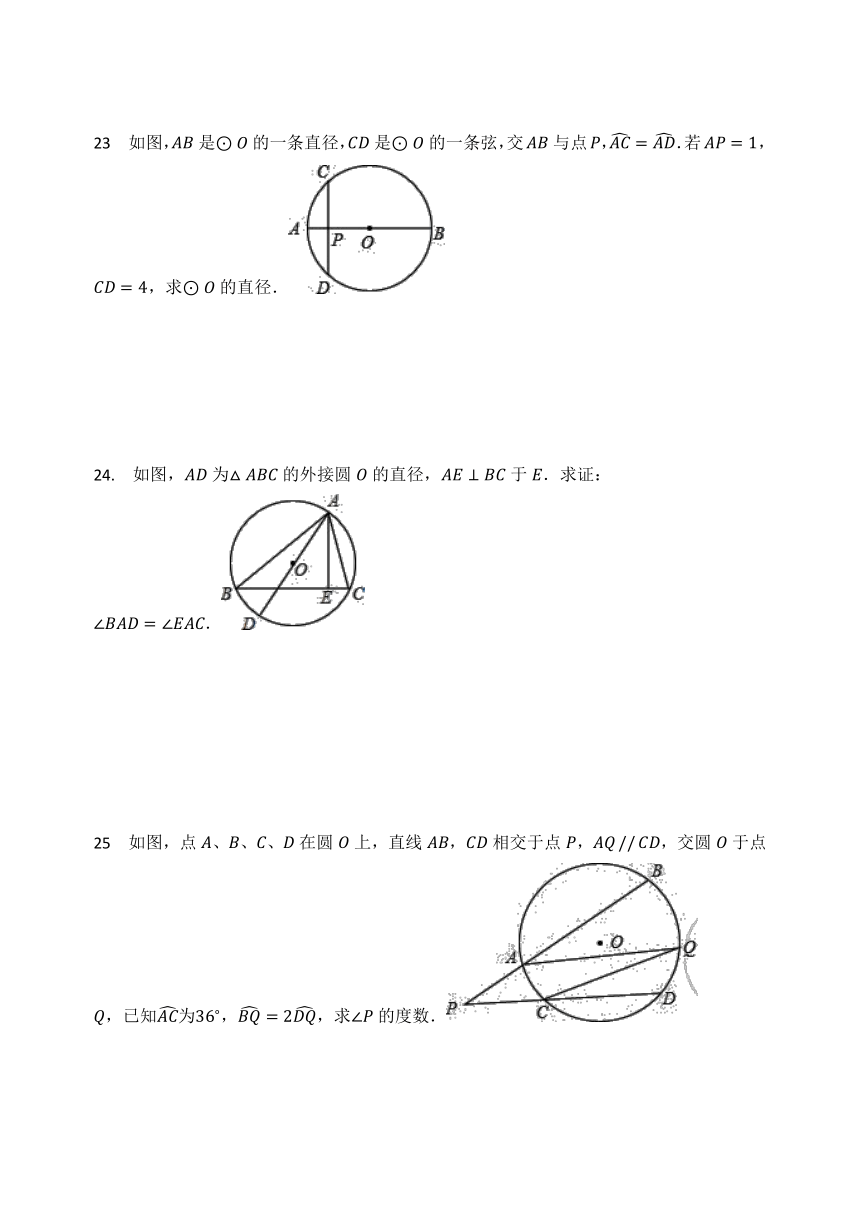
23 如图,AB是⊙O?的一条直径,CD是⊙O的一条弦,交AB与点P,AC=AD.若AP=1,CD=4,求⊙O的直径.
?
24. 如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.
?
25 如图,点A、B、C、D在圆O上,直线AB,CD相交于点P,AQ?//?CD,交圆O于点Q,已知AC为36?,BQ=2DQ,求∠P的度数.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:根据圆的周长公式得:c=πd=2πr
得r=c2π.
故选D.
2.
【答案】
C
【解答】
解:∵ ⊙O的半径分别是3,点P到圆心O的距离为4,
∴ 点P与⊙O的位置关系是:点在圆外.
故选C.
3.
【答案】
C
【解答】
解:∵ 有外接圆的条件四边形必须对角互补,
∴ 只有矩形一定有外接圆,
故选:C.
4.
【答案】
C
【解答】
解:连接OD,过圆心O作OH⊥CD于点H.
∴ DH=CH=12CD(垂径定理);
∵ CD=214,
∴ DH=14.
又∵ AE=6,BE=2,
∴ AB=8,
∴ OA=OD=4(⊙O的半径);
∴ OE=2;
∴ 在Rt△ODH中,OH=OD2-DH2=42-14=2(勾股定理);
在Rt△OEH中,sin∠OEH=OHOE=22,
∴ ∠OEH=45?,
即∠AED=45?.
故选:C.
5.
【答案】
D
【解答】
解:A、只知道圆心,不知道半径,不能确定一个圆,故本选项错误;
B、只知道半径,不知道圆心,不能确定一个圆,故本选项错误;
C、在一条直线上的三点才能确定一个圆,故本选项错误;
D、过不在一直线上的三点可以确定一个圆,故本选项正确.
故选D.
6.
【答案】
B
【解答】
∵ S扇形=12lr,
∴ 120π=12?10π?r,
∴ r=24(cm);
7.
【答案】
B
【解答】
解:根据大角对大边和已知条件,得
甲图中的最大边=乙图中的中间边=丙图中的最小边.
所以它们的周长大小是甲<乙<丙.
故选B.
8.
【答案】
C
【解答】
解:以AB为直径作圆,那么到AB的距离等于5cm的点在两条与AB平行到AB的距离为5的直线上,而这两条直线与圆的交点只有两个.
故选C.
9.
【答案】
C
【解答】
解:经过正九边形的中心O作边AB的垂线OC,
则∠O=20?,
在直角△OBC中,根据三角函数得到BC=OBsin20?=2Rsin20?.
∴ 边长AB=2Rsin20?.
故选C.
10.
【答案】
C
【解答】
解:观察图形可知,出现的小方格需顺时针旋转90?,向右平移至边界.
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
40?
【解答】
由题意得:
AC=AC',
∴ ∠ACC'=∠AC'C;
∵ CC'?//?AB,且∠BAC=70?,
∴ ∠ACC'=∠AC'C=∠BAC=70?,
∴ ∠CAC'=180?-2×70?=40?;
由题意知:∠BAB'=∠CAC'=40?,
12.
【答案】
45
【解答】
设扇形的圆心角为n?,
根据扇形的面积公式得,nπ×42360=2π,
∴ n=45?,
13.
【答案】
3
【解答】
∵ ∠ACB=∠ACD=90?,
∴ Rt△ABC和Rt△ACD分别是AB,AD的中点,
∴ 两三角形的外心距为△ABD的中位线,即为12BD=3.
14.
【答案】
90
【解答】
解:该图形围绕自己的旋转中心,最少顺时针旋转360?÷4=90?后,能与其自身重合.
故答案为:90.
15.
【答案】
90?
【解答】
解:∵ 时针从上午的8时到11时共旋转了3个格,每相邻两个格之间的夹角是30?,
∴ 时针旋转的旋转角=30?×3=90?.
故答案为:90?.
16.
【答案】
8
【解答】
解:设扇形的半径为r,
根据扇形面积公式S=12lr=12×4×4=8.
故答案为:8.
17.
【答案】
(2165,?125)
【解答】
解:∵ 点A(-3,?0)、B(0,?4),
∴ OA=3,OB=4,
∴ AB=32+42=5,
在第②个三角形中,如图,作DH⊥x轴于H,
EF=AB=5,DE=OB=4,DF=3,
∵ 12DH?EF=12DE?DF,
∴ DH=3×45=125,
∴ EH=DE2-DH2=165,
∵ 11=3×3+2,
∴ 第11个三角形与第②个三角形的直角顶点的纵坐标相同,都是125,
第11个三角形的直角顶点的横坐标为3(3+5+4)+4+165=2165,
即第11个三角形的直角顶点的坐标为(2165,?125).
故答案为(2165,?125).
18.
【答案】
5
【解答】
解:∵ 直角三角形的两直角边长是6cm和8cm,
∴ 斜边的长=62+82=10cm,
∴ 外接圆半径=5cm.
故答案为:5.
19.
【答案】
正方形AGOF,绕点O旋转
【解答】
解:根据旋转的意义,正方形AGOF围绕O点顺时针旋转90?可得到正方形OFDE,再旋转90?,可得到正方形OECH,因此可以看作是由基本图形正方形AGOF经绕点O旋转得到的.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
20
【答案】
解:如图所示:这个图案像风车.
【解答】
解:如图所示:这个图案像风车.
21.
【答案】
解:△ABE为等边三角形;证明如下:如图,
∵ 四边形ABCD为矩形,
∴ AB=DC,∠CDA=∠DAB=90?;
由旋转变换的性质知:
DF=AF,∠DFA=60?,AE=CD,∠EAF=∠CDF,
∴ △ADF为等边三角形,AE=AB,
∴ ∠FDA=∠FAD=60?,
∴ ∠CDF=∠BAF=30?,∠EAF=∠CDF=30?,
∴ ∠EAB=60?,而EA=EB,
∴ △ABE为等边三角形.
【解答】
解:△ABE为等边三角形;证明如下:如图,
∵ 四边形ABCD为矩形,
∴ AB=DC,∠CDA=∠DAB=90?;
由旋转变换的性质知:
DF=AF,∠DFA=60?,AE=CD,∠EAF=∠CDF,
∴ △ADF为等边三角形,AE=AB,
∴ ∠FDA=∠FAD=60?,
∴ ∠CDF=∠BAF=30?,∠EAF=∠CDF=30?,
∴ ∠EAB=60?,而EA=EB,
∴ △ABE为等边三角形.
22
【答案】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
【解答】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
23
【答案】
解:连接OC,设OC=x,
∵ AC=AD,
∴ CD⊥AB,
∵ CD=4,
∴ CP=2,
∵ AP=1,
∴ OP=x-1,
在Rt△CPO中,
x2=22+(x-1)2,
解得:x=52,
∴ ⊙O的直径为2×52=5.
【解答】
解:连接OC,设OC=x,
∵ AC=AD,
∴ CD⊥AB,
∵ CD=4,
∴ CP=2,
∵ AP=1,
∴ OP=x-1,
在Rt△CPO中,
x2=22+(x-1)2,
解得:x=52,
∴ ⊙O的直径为2×52=5.
24
【答案】
证明:连接BD,
∵ AD是△ABC的外接圆直径,
∴ ∠ABD=90?.
∴ ∠BAD+∠D=90?.
∵ AE是△ABC的高,
∴ ∠AEC=90?.
∴ ∠CAE+∠ACB=90?.
∵ ∠D=∠ACB,
∴ ∠BAD=∠EAC.
【解答】
证明:连接BD,
∵ AD是△ABC的外接圆直径,
∴ ∠ABD=90?.
∴ ∠BAD+∠D=90?.
∵ AE是△ABC的高,
∴ ∠AEC=90?.
∴ ∠CAE+∠ACB=90?.
∵ ∠D=∠ACB,
∴ ∠BAD=∠EAC.
25
【答案】
解:∵ AQ?//?CD,
∴ DQ=AC=36?,
∵ BQ=2DQ=72?,
∴ ∠BAQ=12×72?=36?,
∵ AQ?//?CD,
∴ ∠P=∠BAQ,
∴ ∠P=36?.
【解答】
解:∵ AQ?//?CD,
∴ DQ=AC=36?,
∵ BQ=2DQ=72?,
∴ ∠BAQ=12×72?=36?,
∵ AQ?//?CD,
∴ ∠P=∠BAQ,
∴ ∠P=36?.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 如果⊙O的周长为C,那么它的半径R为( )
A.2πC B.πC C.Cπ D.C2π
?
2. 已知⊙O的半径分别是3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )
A.点在圆内 B.点在圆上 C.点在圆外 D.无法确定
?
3. 下列四边形中,一定有外接圆的是( )
A.平行四边形 B.菱形 C.矩形 D.梯形
?
4. 如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=214,则∠AED的度数是( )
A.30? B.60? C.45? D.36?
?
5. 可以作圆,且只可以作一个圆的条件是( )
A.已知圆心 B.已知半径
C.过三个已知点 D.过不在一直线上的三点
?
6. 扇形的弧长为10πcm,面积为120πcm2,则扇形的半径是( )
A.12cm B.24cm C.28cm D.30cm
?
7. 如图所示,甲、乙、丙三个三角形,每个三角形的内角均为55?、60?、65?.若AB=DE=GH,则甲、乙、丙周长的关系为( )
A.甲=乙=丙 B.甲<乙<丙 C.甲<丙<乙 D.丙<乙<甲
?
8. 已知AB=10cm,以AB为直径作圆,那么在此圆上到AB的距离等于5cm的点共有( )
A.无数个 B.1个 C.2个 D.4个
?
9. 1996年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( )
A.Rsin20? B.Rsin40? C.2Rsin20? D.2Rsin40?
?
10. 在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( )
A.顺时针旋转90?,向下平移
B.逆时针旋转90?,向下平移
C.顺时针旋转90?,向右平移
D.逆时针旋转90?,向右平移
二、 填空题 (本题共计9小题 ,每题 3 分 ,共计27分 , ) ?
11. 如图,在△ABC中,∠BAC=70?,在同一平面内将△ABC绕点A旋转到△AB'C'的位置,使得CC'?//?AB,则∠BAB'=________.
?
12. 一个扇形的面积为2πcm2,半径OA为4cm,则这个扇形的圆心角为________??.
?
13. 我们把两个三角形的外心之间的距离叫做外心距.在Rt△ABC和Rt△ACD中,∠ACB=∠ACD=90?,点D在边BC的延长线上,如果BC=DC=3,那么△ABC和△ACD的外心距是________.
?
14. 如图,星形图形绕着中心最小旋转________??能与自身重合.
?
15. 时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是________.
?
16. 弧长等于半径的扇形称为“等边扇形”,则半径为4的“等边扇形”面积为________.
?
17. 如图,已知点A(-3,?0)、B(0,?4),对△OAB连续作旋转变换,依次得到三角形①、②、…则第11个三角形的直角顶点的坐标为________.
?
18. 直角三角形的两直角边长是6cm和8cm,则其外接圆半径是________cm.
?
19. 如图可以看作是由基本图形________经________得到的.
?
三、 解答题 (本题共计 6 小题 ,共计63分 , ) ?
20. 在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90?,180?,270?得到的图形组成的,请你画出这个图案,并描述这个图案像什么.
?
21. 如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60?后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
?22 如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20?,求∠ACO的度数.
?
23 如图,AB是⊙O?的一条直径,CD是⊙O的一条弦,交AB与点P,AC=AD.若AP=1,CD=4,求⊙O的直径.
?
24. 如图,AD为△ABC的外接圆O的直径,AE⊥BC于E.求证:∠BAD=∠EAC.
?
25 如图,点A、B、C、D在圆O上,直线AB,CD相交于点P,AQ?//?CD,交圆O于点Q,已知AC为36?,BQ=2DQ,求∠P的度数.
参考答案与试题解析
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:根据圆的周长公式得:c=πd=2πr
得r=c2π.
故选D.
2.
【答案】
C
【解答】
解:∵ ⊙O的半径分别是3,点P到圆心O的距离为4,
∴ 点P与⊙O的位置关系是:点在圆外.
故选C.
3.
【答案】
C
【解答】
解:∵ 有外接圆的条件四边形必须对角互补,
∴ 只有矩形一定有外接圆,
故选:C.
4.
【答案】
C
【解答】
解:连接OD,过圆心O作OH⊥CD于点H.
∴ DH=CH=12CD(垂径定理);
∵ CD=214,
∴ DH=14.
又∵ AE=6,BE=2,
∴ AB=8,
∴ OA=OD=4(⊙O的半径);
∴ OE=2;
∴ 在Rt△ODH中,OH=OD2-DH2=42-14=2(勾股定理);
在Rt△OEH中,sin∠OEH=OHOE=22,
∴ ∠OEH=45?,
即∠AED=45?.
故选:C.
5.
【答案】
D
【解答】
解:A、只知道圆心,不知道半径,不能确定一个圆,故本选项错误;
B、只知道半径,不知道圆心,不能确定一个圆,故本选项错误;
C、在一条直线上的三点才能确定一个圆,故本选项错误;
D、过不在一直线上的三点可以确定一个圆,故本选项正确.
故选D.
6.
【答案】
B
【解答】
∵ S扇形=12lr,
∴ 120π=12?10π?r,
∴ r=24(cm);
7.
【答案】
B
【解答】
解:根据大角对大边和已知条件,得
甲图中的最大边=乙图中的中间边=丙图中的最小边.
所以它们的周长大小是甲<乙<丙.
故选B.
8.
【答案】
C
【解答】
解:以AB为直径作圆,那么到AB的距离等于5cm的点在两条与AB平行到AB的距离为5的直线上,而这两条直线与圆的交点只有两个.
故选C.
9.
【答案】
C
【解答】
解:经过正九边形的中心O作边AB的垂线OC,
则∠O=20?,
在直角△OBC中,根据三角函数得到BC=OBsin20?=2Rsin20?.
∴ 边长AB=2Rsin20?.
故选C.
10.
【答案】
C
【解答】
解:观察图形可知,出现的小方格需顺时针旋转90?,向右平移至边界.
故选C.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
40?
【解答】
由题意得:
AC=AC',
∴ ∠ACC'=∠AC'C;
∵ CC'?//?AB,且∠BAC=70?,
∴ ∠ACC'=∠AC'C=∠BAC=70?,
∴ ∠CAC'=180?-2×70?=40?;
由题意知:∠BAB'=∠CAC'=40?,
12.
【答案】
45
【解答】
设扇形的圆心角为n?,
根据扇形的面积公式得,nπ×42360=2π,
∴ n=45?,
13.
【答案】
3
【解答】
∵ ∠ACB=∠ACD=90?,
∴ Rt△ABC和Rt△ACD分别是AB,AD的中点,
∴ 两三角形的外心距为△ABD的中位线,即为12BD=3.
14.
【答案】
90
【解答】
解:该图形围绕自己的旋转中心,最少顺时针旋转360?÷4=90?后,能与其自身重合.
故答案为:90.
15.
【答案】
90?
【解答】
解:∵ 时针从上午的8时到11时共旋转了3个格,每相邻两个格之间的夹角是30?,
∴ 时针旋转的旋转角=30?×3=90?.
故答案为:90?.
16.
【答案】
8
【解答】
解:设扇形的半径为r,
根据扇形面积公式S=12lr=12×4×4=8.
故答案为:8.
17.
【答案】
(2165,?125)
【解答】
解:∵ 点A(-3,?0)、B(0,?4),
∴ OA=3,OB=4,
∴ AB=32+42=5,
在第②个三角形中,如图,作DH⊥x轴于H,
EF=AB=5,DE=OB=4,DF=3,
∵ 12DH?EF=12DE?DF,
∴ DH=3×45=125,
∴ EH=DE2-DH2=165,
∵ 11=3×3+2,
∴ 第11个三角形与第②个三角形的直角顶点的纵坐标相同,都是125,
第11个三角形的直角顶点的横坐标为3(3+5+4)+4+165=2165,
即第11个三角形的直角顶点的坐标为(2165,?125).
故答案为(2165,?125).
18.
【答案】
5
【解答】
解:∵ 直角三角形的两直角边长是6cm和8cm,
∴ 斜边的长=62+82=10cm,
∴ 外接圆半径=5cm.
故答案为:5.
19.
【答案】
正方形AGOF,绕点O旋转
【解答】
解:根据旋转的意义,正方形AGOF围绕O点顺时针旋转90?可得到正方形OFDE,再旋转90?,可得到正方形OECH,因此可以看作是由基本图形正方形AGOF经绕点O旋转得到的.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
20
【答案】
解:如图所示:这个图案像风车.
【解答】
解:如图所示:这个图案像风车.
21.
【答案】
解:△ABE为等边三角形;证明如下:如图,
∵ 四边形ABCD为矩形,
∴ AB=DC,∠CDA=∠DAB=90?;
由旋转变换的性质知:
DF=AF,∠DFA=60?,AE=CD,∠EAF=∠CDF,
∴ △ADF为等边三角形,AE=AB,
∴ ∠FDA=∠FAD=60?,
∴ ∠CDF=∠BAF=30?,∠EAF=∠CDF=30?,
∴ ∠EAB=60?,而EA=EB,
∴ △ABE为等边三角形.
【解答】
解:△ABE为等边三角形;证明如下:如图,
∵ 四边形ABCD为矩形,
∴ AB=DC,∠CDA=∠DAB=90?;
由旋转变换的性质知:
DF=AF,∠DFA=60?,AE=CD,∠EAF=∠CDF,
∴ △ADF为等边三角形,AE=AB,
∴ ∠FDA=∠FAD=60?,
∴ ∠CDF=∠BAF=30?,∠EAF=∠CDF=30?,
∴ ∠EAB=60?,而EA=EB,
∴ △ABE为等边三角形.
22
【答案】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
【解答】
解:∵ E是AD的中点,
∴ OE⊥AD,
∴ ∠AEO=90?,
∵ ∠BAD=20?,
∴ ∠AOE=70?,
∵ OA=OC,
∴ ∠OAC=∠AOC,
∴ ∠AOC=12(180?-∠AOC)=12(180?-70?)=55?.
23
【答案】
解:连接OC,设OC=x,
∵ AC=AD,
∴ CD⊥AB,
∵ CD=4,
∴ CP=2,
∵ AP=1,
∴ OP=x-1,
在Rt△CPO中,
x2=22+(x-1)2,
解得:x=52,
∴ ⊙O的直径为2×52=5.
【解答】
解:连接OC,设OC=x,
∵ AC=AD,
∴ CD⊥AB,
∵ CD=4,
∴ CP=2,
∵ AP=1,
∴ OP=x-1,
在Rt△CPO中,
x2=22+(x-1)2,
解得:x=52,
∴ ⊙O的直径为2×52=5.
24
【答案】
证明:连接BD,
∵ AD是△ABC的外接圆直径,
∴ ∠ABD=90?.
∴ ∠BAD+∠D=90?.
∵ AE是△ABC的高,
∴ ∠AEC=90?.
∴ ∠CAE+∠ACB=90?.
∵ ∠D=∠ACB,
∴ ∠BAD=∠EAC.
【解答】
证明:连接BD,
∵ AD是△ABC的外接圆直径,
∴ ∠ABD=90?.
∴ ∠BAD+∠D=90?.
∵ AE是△ABC的高,
∴ ∠AEC=90?.
∴ ∠CAE+∠ACB=90?.
∵ ∠D=∠ACB,
∴ ∠BAD=∠EAC.
25
【答案】
解:∵ AQ?//?CD,
∴ DQ=AC=36?,
∵ BQ=2DQ=72?,
∴ ∠BAQ=12×72?=36?,
∵ AQ?//?CD,
∴ ∠P=∠BAQ,
∴ ∠P=36?.
【解答】
解:∵ AQ?//?CD,
∴ DQ=AC=36?,
∵ BQ=2DQ=72?,
∴ ∠BAQ=12×72?=36?,
∵ AQ?//?CD,
∴ ∠P=∠BAQ,
∴ ∠P=36?.
同课章节目录
