2019--2020学年浙江省九年级上册数学(浙教版)《相似三角形》试题分类——填空题(Word版 含解析)
文档属性
| 名称 | 2019--2020学年浙江省九年级上册数学(浙教版)《相似三角形》试题分类——填空题(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 157.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 22:30:20 | ||
图片预览




文档简介
2019--2020学年浙江省九年级上册数学(浙教版)《相似三角形》试题分类——填空题
1.(2019秋?海曙区期末)如图,矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,则CF的长为
.
2.(2019秋?拱墅区校级期末)如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为
.
3.(2019秋?拱墅区校级期末)如图所示,已知△ABC中,BC=12,BC边上的高h=6,D为BC上一点,EF∥BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为
.
4.(2019秋?玉环市期末)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=
.
5.(2019秋?玉环市期末)如图,△ABC内接于半径为2的半⊙O,AB为直径,点M是弧AC的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,则∠MDA=
.若点D恰好为BM的中点时,ME的长为
.
6.(2019秋?江干区期末)由4m=7n,可得比例式:
.
7.(2019秋?江干区期末)如图,已知?ABCD中,E是BC的三等分点,连结AE与对角线BD交于点F,则S△BEF:S△ABF:S△ADF:S四边形CDFE=
.
8.(2019秋?丽水期末)如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为
(用含x的代数式表示);
(2)设EK=2KF,则的值为
.
9.(2019秋?江北区期末)如图,在△ABC中,D、E、F分别在AB、AC、BC上,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为
.
10.(2019秋?滨江区期末)如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=120cm,CD=600cm,则树AB的高度为
cm.
11.(2019秋?丽水期末)已知线段a=4,b=16,则a,b的比例中项线段的长是
.
12.(2019秋?嘉兴期末)如图,等腰△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则的值等于
.
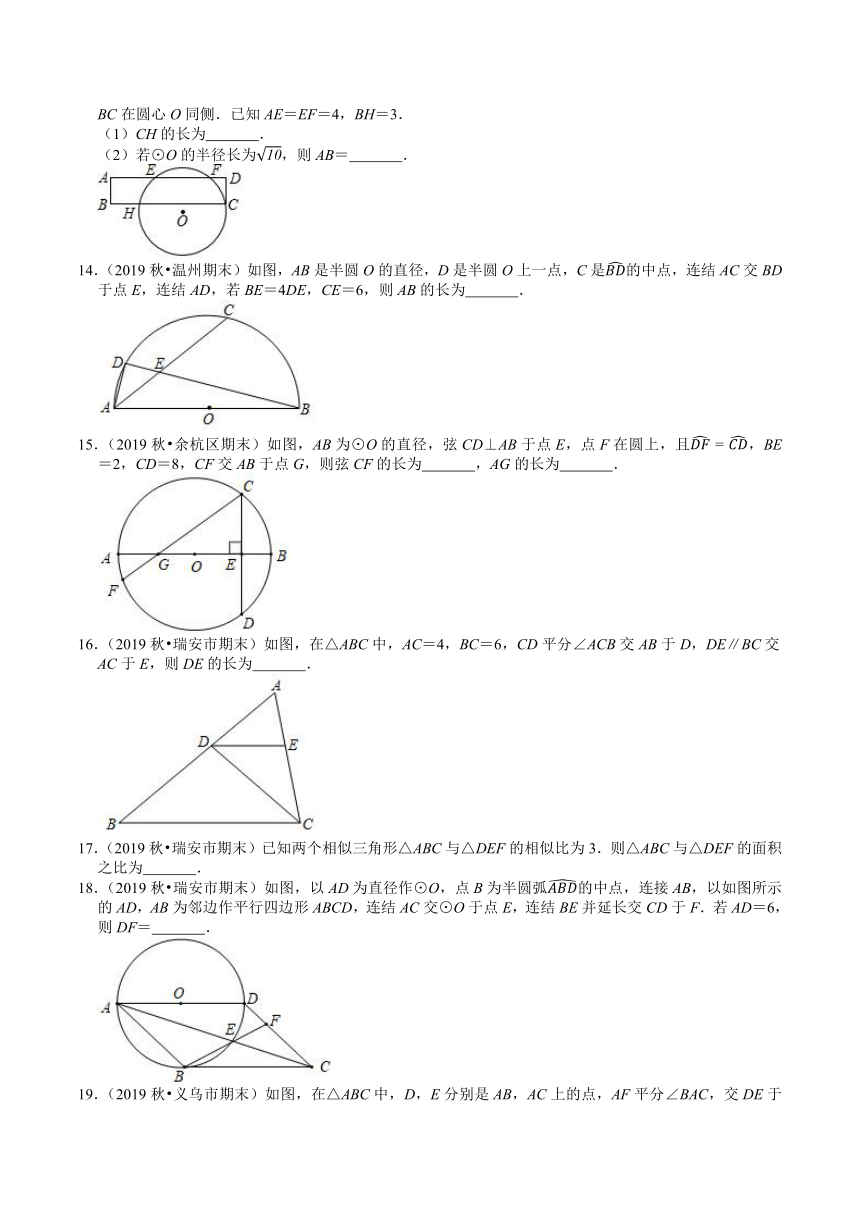
13.(2019秋?萧山区期末)如图,⊙O经过矩形ABCD的顶点C,且与AD,BC相交于点E,F,H,AD,BC在圆心O同侧.已知AE=EF=4,BH=3.
(1)CH的长为
.
(2)若⊙O的半径长为,则AB=
.
14.(2019秋?温州期末)如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连结AC交BD于点E,连结AD,若BE=4DE,CE=6,则AB的长为
.
15.(2019秋?余杭区期末)如图,AB为⊙O的直径,弦CD⊥AB于点E,点F在圆上,且,BE=2,CD=8,CF交AB于点G,则弦CF的长为
,AG的长为
.
16.(2019秋?瑞安市期末)如图,在△ABC中,AC=4,BC=6,CD平分∠ACB交AB于D,DE∥BC交AC于E,则DE的长为
.
17.(2019秋?瑞安市期末)已知两个相似三角形△ABC与△DEF的相似比为3.则△ABC与△DEF的面积之比为
.
18.(2019秋?瑞安市期末)如图,以AD为直径作⊙O,点B为半圆弧的中点,连接AB,以如图所示的AD,AB为邻边作平行四边形ABCD,连结AC交⊙O于点E,连结BE并延长交CD于F.若AD=6,则DF=
.
19.(2019秋?义乌市期末)如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=3:2,则DE:BC=
.
20.(2019秋?北仑区期末)已知:线段a=4cm,b=9cm,c是线段a,b的比例中项,则线段c=
cm.
21.(2019秋?诸暨市期末)已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1
S2(填<、≤、=、>或≥).
22.(2019秋?拱墅区校级期末)一个三角形的三边之比为3:6:4,与它相似的三角形的周长为39cm,则与它相似的三角形的最长边为
.
23.(2019秋?长兴县期末)已知线段c是线段a、b的比例中项,且a=4,b=9,则线段c的长度为
.
2019--2020学年浙江省九年级上册数学(浙教版)《相似三角形》试题分类——填空题
参考答案与试题解析
一.填空题(共23小题)
1.【答案】见试题解答内容
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=2,AB=DC=4,
∵四边形EFBC是矩形,
∴EF=BC=2,CF=BE,
∵余下的矩形EBCF∽矩形BCDA,
∴,
即,
∴CF=1,
故答案为:1.
2.【答案】见试题解答内容
【解答】解:根据题意得:OA=1,OB=2,AB,
∴当AB与AC对应时,有或者,
∴AC或AC=5,
∵C在格点上,
∴AC(不合题意),则AC=5,
∴C点坐标为(4,4),
同理当AB与BC对应时,可求得BC或者BC=5,也是只有后者符合题意,此时C点坐标为(5,2)
∴C点坐标为(5,2)或(4,4).
故答案为:(4,4)或(5,2).
3.【答案】见试题解答内容
【解答】解:过点A向BC作AH⊥BC于点H,
∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴,
即EF=2(6﹣x),
所以y2(6﹣x)x=﹣x2+6x.(0<x<6),
该函数图象是抛物线的一部分,
故答案为:抛物线的一部分.
4.【答案】见试题解答内容
【解答】解:作DF∥AE交BC于F,如图,
∵OE∥DF,
∴1,
即BE=EF,
∵DF∥AE,
∴,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3.
故答案为1:3.
5.【答案】见试题解答内容
【解答】解:(1)∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵,
∴∠CBM=∠ABM,
∵∠CAD=∠BAD,
∴∠DAB+∠DBA(∠CAB+∠CBA)=45°,
∴∠MDA=45°,
故答为45°.
(2)如图作MH⊥AB于M,连接AM,OM,OM交AC于F.
∵AB是直径,
∴∠AMB=90°,∠C=90°,
∵∠ADM=180°﹣∠ADB=45°,
∴MA=MD,
∵DM=DB,
∴BM=2AM,设AM=x,则BM=2x,
∵AB=4,
∴x2+4x2=160,
∴x=4(负根已经舍弃),
∴AM=4,BM=8,
∵?AM?BM?AB?MH,
∴MH,
∴OH,
∵,
∴OM⊥AC,
∴AF=FC,
∵OA=OB,
∴BC∥OM,BC=2OF,
∵∠OHM=∠OFA=90°,∠AOF=∠MOH,OA=OM,
∴△OAF≌△OMH(AAS),
∴OF=OH,
∴BC=2OF,MF=2,
∵BC∥OM,
∴△MEF∽△BEC,
∴,即,
∴ME=2,
故答案为45°,2.
6.【答案】见试题解答内容
【解答】解:∵4m=7n,
∴等式两边都除以4n得:,
故答案为:.
7.【答案】见试题解答内容
【解答】解:∵E是BC的三等分点,
∴,
在?ABCD中,∵AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴,
∴S△BEF:S△ABF:S△ADF=1:3:9,
设S△BEF=k,S△ABF=3k,S△ADF=9k,
∴S△ABF+S△ADFS四边形ABCD=S△BEF+S四边形CDFE=12k,
∴四边形CDFE=12k﹣k=11k,
∴S△BEF:S△ABF:S△ADF:S四边形CDFE=1:3:9:11,
故答案为:1:3:9:11.
8.【答案】见试题解答内容
【解答】(1)解:∵正方形ABCD的边长为1,BM=x,
∴AM,
∵点N是AM的中点,
∴AN,
∵EF⊥AM,
∴∠ANE=90°,
∴∠ANE=∠ABM=90°,
∵∠EAN=∠MAB,
∴△AEN∽△AMB,
∴,即,
∴AE,
故答案为;
(2)解:如图,连接AK、MK、CK,
由正方形的轴对称性△ABK≌△CBK,
∴AK=CK,∠KAB=∠KCB,
∵EF⊥AM,N为AM中点,
∴AK=MK,
∴MK=CK,∠KMC=∠KCM,
∴∠KAB=∠KMC,
∵∠KMB+∠KMC=180°,
∴∠KMB+∠KAB=180°,
又∵四边形ABMK的内角和为360°,∠ABM=90°,
∴∠AKM=90°,
在Rt△AKM中,AM为斜边,N为AM的中点,
∴KNAM=AN,
∴,
∵△AEN∽△AMB,
∴x,
∴x,
∵∠EBK=∠KDF=45°,∠EKB=∠FKD,
∴△EKB∽△FKD,
∴,
∵AE,
∴BE=1,
∴DF,
∴CF=1﹣DF,
连接AF、MF,
∵EF⊥AM,N为AM中点,
∴AF=MF,
∴AD2+DF2=MC2+CF2,即12+()2=(1﹣x)2+()2,
整理得,3x2﹣4x+1=0,
解得x或1(舍去),
∴
故答案为.
9.【答案】见试题解答内容
【解答】解:∵DE∥BC,
∴,∠AED=∠C,
∵EF∥AB,
∴∠CEF=∠A,又∠AED=∠C,
∴△AED∽△ECF,
∴,即,
解得,DE=10,
故答案为:10.
10.【答案】见试题解答内容
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm,EF=15cm,AC=120cm,CD=600cm,
∴,
∴BC=300cm,
∴AB=AC+BC=120+300=420cm,
故答案为:420.
11.【答案】见试题解答内容
【解答】解:设线段a,b的比例中项为c,
∵c是长度分别为4、16的两条线段的比例中项,
∴c2=ab=4×16,
∴c2=64,
∴c=8(负数舍去),
∴a、b的比例中项为8;
故答案为:8.
12.【答案】见试题解答内容
【解答】解:∵AB=AC,
∴∠ABC=∠C(180°﹣∠A)(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BD=BC,
∵∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴,即
,
∴点D为AC的黄金分割点,
∴ADAC,
∴CD=AC﹣AD=ACACAC,
∴;
故答案为:.
13.【答案】见试题解答内容
【解答】解:(1)
过O作OM⊥AD于M,交BC于N,
∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,AD∥BC,
∴ON⊥BC,
即∠A=∠B=∠BNM=90°,
∴四边形ABNM是矩形,
∴AB=MN,AM=BN,
∵EF=4,OM⊥EF,OM过O,
∴EM=FM=2,
∵AE=4,
∴AM=4+2=6,
即OB=AM=6,
∵BH=3,
∴HN=6﹣3=3,
由垂径定理得:CH=2HN=6,
故答案为:6;
(2)
连接OH和OE,
在Rt△OHN中,由勾股定理得:ON1,
在Rt△OEM中,由勾股定理得OM,
即AB=MN1,
故答案为:1.
14.【答案】见试题解答内容
【解答】解:如图,连接OC交BD于K,连结BC.
∵,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK?EB,
∴36=1.5k×4k,
∵k>0,
∴k,
∴BC2,
∴AB4.
故答案为4.
15.【答案】见试题解答内容
【解答】解:连结BC,DF,OC,连结DO并延长交CF于点H,
∵弦CD⊥AB于点E,CD=8,
∴CE4,
设OC=x,则OE=x﹣2,
∵OE2+CE2=OC2,
∴(x﹣2)2+42=x2,
解得x=5,
∴OC=5,
∴OE=5﹣2=3,
∵,
∴DF=CD,∠CFD=∠COB,DH⊥CF,
∴∠FHD=∠OEC=90°,
∴△DHF∽△CEO,
∴,
∴,
∴FH,DH,
∴CF=2FH,
OH=DH﹣OD,
∵∠CFD=∠COB=∠BOD,∠BOD=∠GOH,
∴∠GOH=∠DFH,
∵∠GHO=∠OEC=90°,
∴△GHO∽△CEO,
∴,
∴,
∴OG,
∴AG=OA﹣OG=5.
故答案为:,.
16.【答案】见试题解答内容
【解答】解:∵CD平分∠ACB交AB于D,
∴∠ACD=∠DCB,
又∵DE∥BC,
∴∠EDC=∠DCB,
∴∠ACD=∠EDC,
∴DE=EC,
设DE=x,则AE=4﹣x,
∵DE∥BC,
∴△AED∽△ACB,
∴,
即,
∴x=2.4.
故答案为:2.4.
17.【答案】见试题解答内容
【解答】解:∵△ABC与△DEF的相似比为3,
∴△ABC与△DEF的面积之比为9.
故答案为9.
18.【答案】见试题解答内容
【解答】解:如图,连接BD交AC于O′,连接DE,作FM⊥AC于M,FN⊥DE于N.
∵,
∴AB=BD,
∵AD是直径,
∴∠ABD=∠AED=90°,
∴∠BAD=∠BDA=∠AEB=45°,
∵∠AEB=∠CEF=45°,∠CED=90°,
∴∠FED=∠FEC=45°,
∵FM⊥EC.FN⊥ED,
∴FM=FN,
∴,
∵四边形ABCD是平行四边形,
∴OB=OD,AB∥CD,
∴∠BAO′=∠DCE,
∴tan∠DCE=tan∠O′AB,
∴DF:CF=DE:CE=1:2,
∴AD=6,△ABD是等腰直角三角形,
∴AB=BD=CD=3,
∴DFCD
故答案为.
19.【答案】见试题解答内容
【解答】解:∵∠DAE=∠CAB,∠AED=∠B,
∴△ADE∽△ACB,
∵GA,FA分别是△ADE,△ABC的角平分线,
∴(相似三角形的对应角平分线的比等于相似比),
AG:FG=3:2,
∴AG:AF=3:5,
∴DE:BC=3:5,
故答为3:5.
20.【答案】见试题解答内容
【解答】解:∵c是线段a,b的比例中项,
∴c2=ab,
∵a=4cm,b=9cm,
∴c2=36,
∴c=6cm.
故答案为:6.
21.【答案】见试题解答内容
【解答】解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB?AB,
则S1:S2=AP2:(PB?AB)=1,即S1=S2.
故答案为:=.
22.【答案】见试题解答内容
【解答】解:∵一个三角形的三边之比为3:6:4,
∴与它相似的三角形的三边之比为3:6:4,
∵与它相似的三角形的周长为39cm,
∴与它相似的三角形的最长边为:3918(cm).
故答案为:18cm.
23.【答案】见试题解答内容
【解答】解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,解得c=±6(线段是正数,负值舍去),
故答案为:6.
1.(2019秋?海曙区期末)如图,矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,则CF的长为
.
2.(2019秋?拱墅区校级期末)如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为
.
3.(2019秋?拱墅区校级期末)如图所示,已知△ABC中,BC=12,BC边上的高h=6,D为BC上一点,EF∥BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为
.
4.(2019秋?玉环市期末)如图,在△ABC中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E,则BE:EC=
.
5.(2019秋?玉环市期末)如图,△ABC内接于半径为2的半⊙O,AB为直径,点M是弧AC的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,则∠MDA=
.若点D恰好为BM的中点时,ME的长为
.
6.(2019秋?江干区期末)由4m=7n,可得比例式:
.
7.(2019秋?江干区期末)如图,已知?ABCD中,E是BC的三等分点,连结AE与对角线BD交于点F,则S△BEF:S△ABF:S△ADF:S四边形CDFE=
.
8.(2019秋?丽水期末)如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为
(用含x的代数式表示);
(2)设EK=2KF,则的值为
.
9.(2019秋?江北区期末)如图,在△ABC中,D、E、F分别在AB、AC、BC上,DE∥BC,EF∥AB,AD:BD=5:3,CF=6,则DE的长为
.
10.(2019秋?滨江区期末)如图,小华同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,使斜边DF与地面保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=30cm,EF=15cm,测得边DF离地面的高度AC=120cm,CD=600cm,则树AB的高度为
cm.
11.(2019秋?丽水期末)已知线段a=4,b=16,则a,b的比例中项线段的长是
.
12.(2019秋?嘉兴期末)如图,等腰△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则的值等于
.
13.(2019秋?萧山区期末)如图,⊙O经过矩形ABCD的顶点C,且与AD,BC相交于点E,F,H,AD,BC在圆心O同侧.已知AE=EF=4,BH=3.
(1)CH的长为
.
(2)若⊙O的半径长为,则AB=
.
14.(2019秋?温州期末)如图,AB是半圆O的直径,D是半圆O上一点,C是的中点,连结AC交BD于点E,连结AD,若BE=4DE,CE=6,则AB的长为
.
15.(2019秋?余杭区期末)如图,AB为⊙O的直径,弦CD⊥AB于点E,点F在圆上,且,BE=2,CD=8,CF交AB于点G,则弦CF的长为
,AG的长为
.
16.(2019秋?瑞安市期末)如图,在△ABC中,AC=4,BC=6,CD平分∠ACB交AB于D,DE∥BC交AC于E,则DE的长为
.
17.(2019秋?瑞安市期末)已知两个相似三角形△ABC与△DEF的相似比为3.则△ABC与△DEF的面积之比为
.
18.(2019秋?瑞安市期末)如图,以AD为直径作⊙O,点B为半圆弧的中点,连接AB,以如图所示的AD,AB为邻边作平行四边形ABCD,连结AC交⊙O于点E,连结BE并延长交CD于F.若AD=6,则DF=
.
19.(2019秋?义乌市期末)如图,在△ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=3:2,则DE:BC=
.
20.(2019秋?北仑区期末)已知:线段a=4cm,b=9cm,c是线段a,b的比例中项,则线段c=
cm.
21.(2019秋?诸暨市期末)已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1
S2(填<、≤、=、>或≥).
22.(2019秋?拱墅区校级期末)一个三角形的三边之比为3:6:4,与它相似的三角形的周长为39cm,则与它相似的三角形的最长边为
.
23.(2019秋?长兴县期末)已知线段c是线段a、b的比例中项,且a=4,b=9,则线段c的长度为
.
2019--2020学年浙江省九年级上册数学(浙教版)《相似三角形》试题分类——填空题
参考答案与试题解析
一.填空题(共23小题)
1.【答案】见试题解答内容
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=2,AB=DC=4,
∵四边形EFBC是矩形,
∴EF=BC=2,CF=BE,
∵余下的矩形EBCF∽矩形BCDA,
∴,
即,
∴CF=1,
故答案为:1.
2.【答案】见试题解答内容
【解答】解:根据题意得:OA=1,OB=2,AB,
∴当AB与AC对应时,有或者,
∴AC或AC=5,
∵C在格点上,
∴AC(不合题意),则AC=5,
∴C点坐标为(4,4),
同理当AB与BC对应时,可求得BC或者BC=5,也是只有后者符合题意,此时C点坐标为(5,2)
∴C点坐标为(5,2)或(4,4).
故答案为:(4,4)或(5,2).
3.【答案】见试题解答内容
【解答】解:过点A向BC作AH⊥BC于点H,
∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴,
即EF=2(6﹣x),
所以y2(6﹣x)x=﹣x2+6x.(0<x<6),
该函数图象是抛物线的一部分,
故答案为:抛物线的一部分.
4.【答案】见试题解答内容
【解答】解:作DF∥AE交BC于F,如图,
∵OE∥DF,
∴1,
即BE=EF,
∵DF∥AE,
∴,
∴CF=2EF,
∴BE:EC=BE:3BE=1:3.
故答案为1:3.
5.【答案】见试题解答内容
【解答】解:(1)∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵,
∴∠CBM=∠ABM,
∵∠CAD=∠BAD,
∴∠DAB+∠DBA(∠CAB+∠CBA)=45°,
∴∠MDA=45°,
故答为45°.
(2)如图作MH⊥AB于M,连接AM,OM,OM交AC于F.
∵AB是直径,
∴∠AMB=90°,∠C=90°,
∵∠ADM=180°﹣∠ADB=45°,
∴MA=MD,
∵DM=DB,
∴BM=2AM,设AM=x,则BM=2x,
∵AB=4,
∴x2+4x2=160,
∴x=4(负根已经舍弃),
∴AM=4,BM=8,
∵?AM?BM?AB?MH,
∴MH,
∴OH,
∵,
∴OM⊥AC,
∴AF=FC,
∵OA=OB,
∴BC∥OM,BC=2OF,
∵∠OHM=∠OFA=90°,∠AOF=∠MOH,OA=OM,
∴△OAF≌△OMH(AAS),
∴OF=OH,
∴BC=2OF,MF=2,
∵BC∥OM,
∴△MEF∽△BEC,
∴,即,
∴ME=2,
故答案为45°,2.
6.【答案】见试题解答内容
【解答】解:∵4m=7n,
∴等式两边都除以4n得:,
故答案为:.
7.【答案】见试题解答内容
【解答】解:∵E是BC的三等分点,
∴,
在?ABCD中,∵AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴,
∴S△BEF:S△ABF:S△ADF=1:3:9,
设S△BEF=k,S△ABF=3k,S△ADF=9k,
∴S△ABF+S△ADFS四边形ABCD=S△BEF+S四边形CDFE=12k,
∴四边形CDFE=12k﹣k=11k,
∴S△BEF:S△ABF:S△ADF:S四边形CDFE=1:3:9:11,
故答案为:1:3:9:11.
8.【答案】见试题解答内容
【解答】(1)解:∵正方形ABCD的边长为1,BM=x,
∴AM,
∵点N是AM的中点,
∴AN,
∵EF⊥AM,
∴∠ANE=90°,
∴∠ANE=∠ABM=90°,
∵∠EAN=∠MAB,
∴△AEN∽△AMB,
∴,即,
∴AE,
故答案为;
(2)解:如图,连接AK、MK、CK,
由正方形的轴对称性△ABK≌△CBK,
∴AK=CK,∠KAB=∠KCB,
∵EF⊥AM,N为AM中点,
∴AK=MK,
∴MK=CK,∠KMC=∠KCM,
∴∠KAB=∠KMC,
∵∠KMB+∠KMC=180°,
∴∠KMB+∠KAB=180°,
又∵四边形ABMK的内角和为360°,∠ABM=90°,
∴∠AKM=90°,
在Rt△AKM中,AM为斜边,N为AM的中点,
∴KNAM=AN,
∴,
∵△AEN∽△AMB,
∴x,
∴x,
∵∠EBK=∠KDF=45°,∠EKB=∠FKD,
∴△EKB∽△FKD,
∴,
∵AE,
∴BE=1,
∴DF,
∴CF=1﹣DF,
连接AF、MF,
∵EF⊥AM,N为AM中点,
∴AF=MF,
∴AD2+DF2=MC2+CF2,即12+()2=(1﹣x)2+()2,
整理得,3x2﹣4x+1=0,
解得x或1(舍去),
∴
故答案为.
9.【答案】见试题解答内容
【解答】解:∵DE∥BC,
∴,∠AED=∠C,
∵EF∥AB,
∴∠CEF=∠A,又∠AED=∠C,
∴△AED∽△ECF,
∴,即,
解得,DE=10,
故答案为:10.
10.【答案】见试题解答内容
【解答】解:∵∠DEF=∠BCD=90°,∠D=∠D,
∴△DEF∽△DCB,
∴BC:EF=DC:DE,
∵DE=30cm,EF=15cm,AC=120cm,CD=600cm,
∴,
∴BC=300cm,
∴AB=AC+BC=120+300=420cm,
故答案为:420.
11.【答案】见试题解答内容
【解答】解:设线段a,b的比例中项为c,
∵c是长度分别为4、16的两条线段的比例中项,
∴c2=ab=4×16,
∴c2=64,
∴c=8(负数舍去),
∴a、b的比例中项为8;
故答案为:8.
12.【答案】见试题解答内容
【解答】解:∵AB=AC,
∴∠ABC=∠C(180°﹣∠A)(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BD=BC,
∵∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴,即
,
∴点D为AC的黄金分割点,
∴ADAC,
∴CD=AC﹣AD=ACACAC,
∴;
故答案为:.
13.【答案】见试题解答内容
【解答】解:(1)
过O作OM⊥AD于M,交BC于N,
∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,AD∥BC,
∴ON⊥BC,
即∠A=∠B=∠BNM=90°,
∴四边形ABNM是矩形,
∴AB=MN,AM=BN,
∵EF=4,OM⊥EF,OM过O,
∴EM=FM=2,
∵AE=4,
∴AM=4+2=6,
即OB=AM=6,
∵BH=3,
∴HN=6﹣3=3,
由垂径定理得:CH=2HN=6,
故答案为:6;
(2)
连接OH和OE,
在Rt△OHN中,由勾股定理得:ON1,
在Rt△OEM中,由勾股定理得OM,
即AB=MN1,
故答案为:1.
14.【答案】见试题解答内容
【解答】解:如图,连接OC交BD于K,连结BC.
∵,
∴OC⊥BD,
∵BE=4DE,
∴可以假设DE=k.BE=4k,则DK=BK=2.5k,EK=1.5k,
∵AB是直径,
∴∠ADK=∠DKC=∠ACB=90°,
∴AD∥CK,
∴AE:EC=DE:EK,
∴AE:6=k:1.5k,
∴AE=4,
∵△ECK∽△EBC,
∴EC2=EK?EB,
∴36=1.5k×4k,
∵k>0,
∴k,
∴BC2,
∴AB4.
故答案为4.
15.【答案】见试题解答内容
【解答】解:连结BC,DF,OC,连结DO并延长交CF于点H,
∵弦CD⊥AB于点E,CD=8,
∴CE4,
设OC=x,则OE=x﹣2,
∵OE2+CE2=OC2,
∴(x﹣2)2+42=x2,
解得x=5,
∴OC=5,
∴OE=5﹣2=3,
∵,
∴DF=CD,∠CFD=∠COB,DH⊥CF,
∴∠FHD=∠OEC=90°,
∴△DHF∽△CEO,
∴,
∴,
∴FH,DH,
∴CF=2FH,
OH=DH﹣OD,
∵∠CFD=∠COB=∠BOD,∠BOD=∠GOH,
∴∠GOH=∠DFH,
∵∠GHO=∠OEC=90°,
∴△GHO∽△CEO,
∴,
∴,
∴OG,
∴AG=OA﹣OG=5.
故答案为:,.
16.【答案】见试题解答内容
【解答】解:∵CD平分∠ACB交AB于D,
∴∠ACD=∠DCB,
又∵DE∥BC,
∴∠EDC=∠DCB,
∴∠ACD=∠EDC,
∴DE=EC,
设DE=x,则AE=4﹣x,
∵DE∥BC,
∴△AED∽△ACB,
∴,
即,
∴x=2.4.
故答案为:2.4.
17.【答案】见试题解答内容
【解答】解:∵△ABC与△DEF的相似比为3,
∴△ABC与△DEF的面积之比为9.
故答案为9.
18.【答案】见试题解答内容
【解答】解:如图,连接BD交AC于O′,连接DE,作FM⊥AC于M,FN⊥DE于N.
∵,
∴AB=BD,
∵AD是直径,
∴∠ABD=∠AED=90°,
∴∠BAD=∠BDA=∠AEB=45°,
∵∠AEB=∠CEF=45°,∠CED=90°,
∴∠FED=∠FEC=45°,
∵FM⊥EC.FN⊥ED,
∴FM=FN,
∴,
∵四边形ABCD是平行四边形,
∴OB=OD,AB∥CD,
∴∠BAO′=∠DCE,
∴tan∠DCE=tan∠O′AB,
∴DF:CF=DE:CE=1:2,
∴AD=6,△ABD是等腰直角三角形,
∴AB=BD=CD=3,
∴DFCD
故答案为.
19.【答案】见试题解答内容
【解答】解:∵∠DAE=∠CAB,∠AED=∠B,
∴△ADE∽△ACB,
∵GA,FA分别是△ADE,△ABC的角平分线,
∴(相似三角形的对应角平分线的比等于相似比),
AG:FG=3:2,
∴AG:AF=3:5,
∴DE:BC=3:5,
故答为3:5.
20.【答案】见试题解答内容
【解答】解:∵c是线段a,b的比例中项,
∴c2=ab,
∵a=4cm,b=9cm,
∴c2=36,
∴c=6cm.
故答案为:6.
21.【答案】见试题解答内容
【解答】解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB?AB,
则S1:S2=AP2:(PB?AB)=1,即S1=S2.
故答案为:=.
22.【答案】见试题解答内容
【解答】解:∵一个三角形的三边之比为3:6:4,
∴与它相似的三角形的三边之比为3:6:4,
∵与它相似的三角形的周长为39cm,
∴与它相似的三角形的最长边为:3918(cm).
故答案为:18cm.
23.【答案】见试题解答内容
【解答】解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,解得c=±6(线段是正数,负值舍去),
故答案为:6.
同课章节目录
