名师导学——第6章图形与坐标综合复习题
文档属性
| 名称 | 名师导学——第6章图形与坐标综合复习题 |  | |
| 格式 | rar | ||
| 文件大小 | 502.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-10 20:05:35 | ||
图片预览


文档简介
第6章综合复习课
【课前热身】
1.根据下列表述,能确定位置的是 ( )
A.某电影院2排
B.南京市大桥南路
C.北偏东30°
D.东经118°,北纬40°
2.如图是方格纸上画出的小旗图案,如果用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为 ( )
A.(0,3) B.(2,3)
C.(3,2) D.(3,O)
3.在平面直角坐标系中,点A(-2,3)位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.在平面直角坐标系中,将点(-2,3)向上平移3个单位后的点的坐标是 ( )
A.(2,6) B.(-2,6)
C.(1,3) D.(3,-2)
5.小明从家出发向正东方向走了160m,然后又向正北出发走到离家200m远的地方.小明向正北方向走了 .
6.如图,在平面直角坐标系中,若△A,B,C,与△ABC
是中心对称图形,则对称中心的坐标为 .
【课堂讲练】
典型例题1 已知点P(x,y)在第四象限,且|x|=3,|y|=5,求点P的坐标.
巩固练习1 点P(m+3,m+1)在x轴上,求P点的坐标.
典型例题2 已知两点A(-1,3),B(3,5).点P为x轴上的一个动点.(1)求点A关于2轴对称点A,的坐标;
(2)当PA+PB最小时,画出点P的位置,并求出这个最小值.
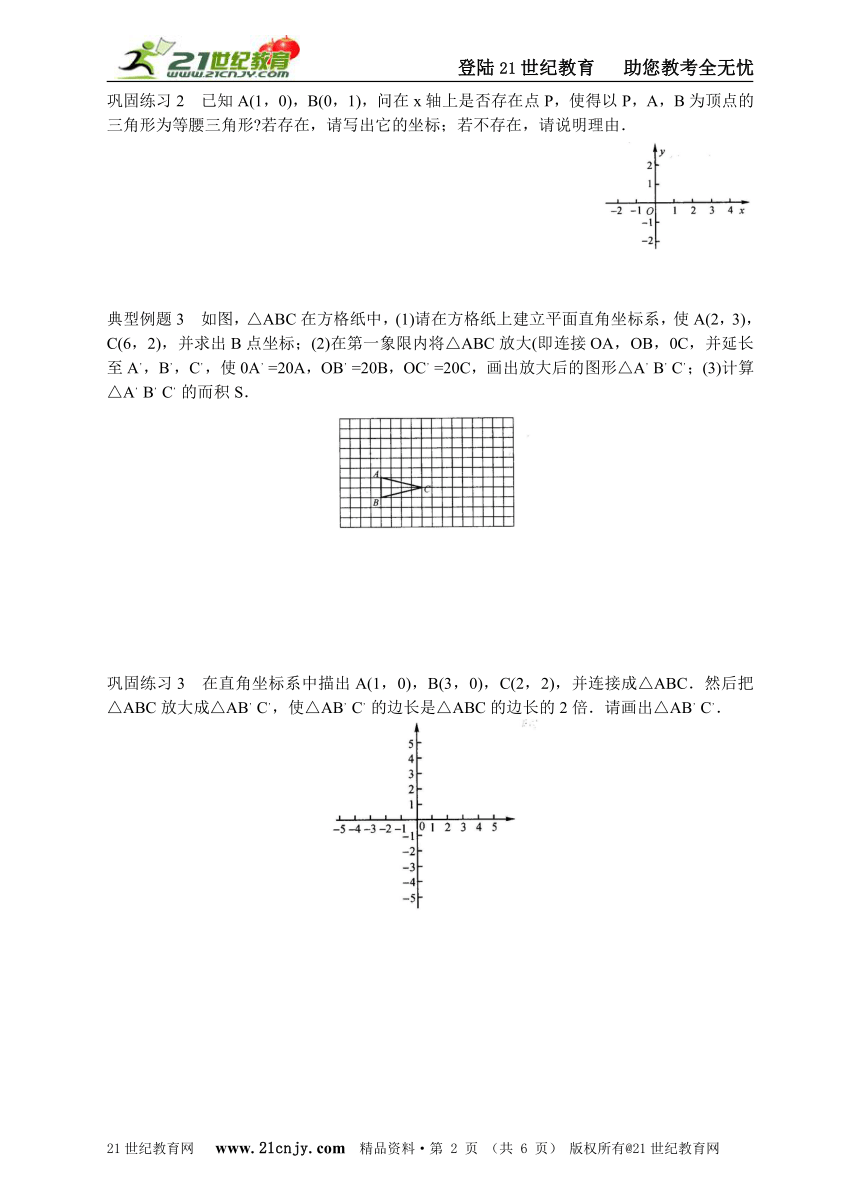
巩固练习2 已知A(1,0),B(0,1),问在x轴上是否存在点P,使得以P,A,B为顶点的三角形为等腰三角形?若存在,请写出它的坐标;若不存在,请说明理由.
典型例题3 如图,△ABC在方格纸中,(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)在第一象限内将△ABC放大(即连接OA,OB,0C,并延长至A,,B,,C,,使0A,=20A,OB,=20B,OC,=20C,画出放大后的图形△A,B,C,;(3)计算△A,B,C,的而积S.
巩固练习3 在直角坐标系中描出A(1,0),B(3,0),C(2,2),并连接成△ABC.然后把△ABC放大成△AB,C,,使△AB,C,的边长是△ABC的边长的2倍.请画出△AB,C,.
典型例题4 如图,已知△ABC的3个顶点的坐标分别
为A(-2,3),B(-6,O),C(-1,O).
(1)将△ABC绕坐标原点逆时针旋转90°.画出图形,直接写出点B的对应点的坐标;
(2)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
巩固练习4 如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面4个点M(3,3),A(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是平行四边形,则该点是 ( )
A.M B.N
C.P D.Q
【跟踪演练】
一、选择题
1.如图,小正方形边长表示1km,点A相对于点B的位置表述正确的是 ( )
A.北偏西45°方向
B.南偏东45°方向
C.北偏西45°方向2km处
D.南偏东45°方向2km处
2.在下列坐标平面内的各点中,在x轴上的点是 ( )
A.(0,3) B.(-3,O)
C.(-1,2) D.(-2,-3)
3.如果<0,那么Q(x,y)所在的象限为 ( )
A.第一象限 B.第二象限
C.第一或三象限 D.第二或四象限
4.将△ABC向右平移3个单位后得到△A,B,C,,若点A
的坐标是(-2,3),则点A,的坐标是 ( )
A.(1,3) B.(-2,6)
C.(-5,3) D.(-2,0)
二、填空题
5.已知点A(a,2a-3)的横坐标和纵坐标满足方程y=x+1,即纵坐标比横坐标大1,则a= .
6.已知点P1(a,3)与P2(-2,-3)关于x轴对称,P3与P1关于原点对称,则a= ,P3的坐标是
7.一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点运动到(1,0),然后接着按图中箭头所示方向运动,即:(0,0)→(1,0)→(1,1)→(0,1)→……,且每秒移动一个单位,那么第20秒时质点所在位置的坐标是 .
三、解答题
8.如图,3架飞机P,Q,R保持相对位置不变飞行,分别写出它们的坐标.30s后,飞机P飞到P,位置,问:飞机Q,R飞到了什么位置?分别写出这3架飞机新位置的坐标.
9.如图:①写出A,B,C三点的坐标:A( ),B( ),C( ).
②若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A,,B,,C,,并依次连接这三个点,所得的△A,B,C,与原△ABC有怎样的位置关系?
③在②的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点A″,B″,C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
10.如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为 (-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ,△ABC的周长是 (结果保留根号);
(3)画出△ABC以点C为旋转中心、旋转180°后的△A,B,C,连结AB,和A,B,说出四边形ABA,B,是何特殊四访形.
参考答案:
【课前热身】
1.D 2.C 3.B 4.8 5.120米 6.(0,O)
【澡堂讲练】
典型例题1 ∵P(x,y)在第四象限 ∴x>0,y<0 ∵|x|=3,|y|=5 ∴x=3,y=-5 ∴P(3,-5)
巩固练习 1由,m+1=0得m=-1 ∴P(2,0)
典型例题2(1)A,(-1,-3)(2)作A,,连结A,B交x轴于P 最小值为A,B==4
巩固练习 2存在,若顶角顶点为P,则P(0,0) 若顶角顶点为A,则P(1-,0)或(+1,0) 若顶角顶点为B,则P(-1,0)
典型例题3 (1)如图,建立坐标系,得B(2,1)
(2)如图
(3)S△A,B,C,=·4·8=16
巩固练习3如图,B,(5,O),C,(3,4)
典型例题4(1)如图,B,(0,-6) (2)D(3,3)或D(-5,-3)或D(-7,3)
巩固练习4 C
【跟踪演练】
1.D 2.B 3.D 4.A 5.4 6.-2 (2,-3)7.(4,4)8.解:Q,(2,3) R,(4,1) P,(4,3),9.①3,4 1,2 5,1 ②关于x轴对称③关于原点O对称 10.(1)略 (2)(-1,1) 2+2 (3)矩形(或长方形)
【课前热身】
1.根据下列表述,能确定位置的是 ( )
A.某电影院2排
B.南京市大桥南路
C.北偏东30°
D.东经118°,北纬40°
2.如图是方格纸上画出的小旗图案,如果用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为 ( )
A.(0,3) B.(2,3)
C.(3,2) D.(3,O)
3.在平面直角坐标系中,点A(-2,3)位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.在平面直角坐标系中,将点(-2,3)向上平移3个单位后的点的坐标是 ( )
A.(2,6) B.(-2,6)
C.(1,3) D.(3,-2)
5.小明从家出发向正东方向走了160m,然后又向正北出发走到离家200m远的地方.小明向正北方向走了 .
6.如图,在平面直角坐标系中,若△A,B,C,与△ABC
是中心对称图形,则对称中心的坐标为 .
【课堂讲练】
典型例题1 已知点P(x,y)在第四象限,且|x|=3,|y|=5,求点P的坐标.
巩固练习1 点P(m+3,m+1)在x轴上,求P点的坐标.
典型例题2 已知两点A(-1,3),B(3,5).点P为x轴上的一个动点.(1)求点A关于2轴对称点A,的坐标;
(2)当PA+PB最小时,画出点P的位置,并求出这个最小值.
巩固练习2 已知A(1,0),B(0,1),问在x轴上是否存在点P,使得以P,A,B为顶点的三角形为等腰三角形?若存在,请写出它的坐标;若不存在,请说明理由.
典型例题3 如图,△ABC在方格纸中,(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)在第一象限内将△ABC放大(即连接OA,OB,0C,并延长至A,,B,,C,,使0A,=20A,OB,=20B,OC,=20C,画出放大后的图形△A,B,C,;(3)计算△A,B,C,的而积S.
巩固练习3 在直角坐标系中描出A(1,0),B(3,0),C(2,2),并连接成△ABC.然后把△ABC放大成△AB,C,,使△AB,C,的边长是△ABC的边长的2倍.请画出△AB,C,.
典型例题4 如图,已知△ABC的3个顶点的坐标分别
为A(-2,3),B(-6,O),C(-1,O).
(1)将△ABC绕坐标原点逆时针旋转90°.画出图形,直接写出点B的对应点的坐标;
(2)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
巩固练习4 如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面4个点M(3,3),A(3,-3),P(-3,0),Q(-3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是平行四边形,则该点是 ( )
A.M B.N
C.P D.Q
【跟踪演练】
一、选择题
1.如图,小正方形边长表示1km,点A相对于点B的位置表述正确的是 ( )
A.北偏西45°方向
B.南偏东45°方向
C.北偏西45°方向2km处
D.南偏东45°方向2km处
2.在下列坐标平面内的各点中,在x轴上的点是 ( )
A.(0,3) B.(-3,O)
C.(-1,2) D.(-2,-3)
3.如果<0,那么Q(x,y)所在的象限为 ( )
A.第一象限 B.第二象限
C.第一或三象限 D.第二或四象限
4.将△ABC向右平移3个单位后得到△A,B,C,,若点A
的坐标是(-2,3),则点A,的坐标是 ( )
A.(1,3) B.(-2,6)
C.(-5,3) D.(-2,0)
二、填空题
5.已知点A(a,2a-3)的横坐标和纵坐标满足方程y=x+1,即纵坐标比横坐标大1,则a= .
6.已知点P1(a,3)与P2(-2,-3)关于x轴对称,P3与P1关于原点对称,则a= ,P3的坐标是
7.一个质点在第一象限及x轴,y轴上运动,在第一秒钟,它从原点运动到(1,0),然后接着按图中箭头所示方向运动,即:(0,0)→(1,0)→(1,1)→(0,1)→……,且每秒移动一个单位,那么第20秒时质点所在位置的坐标是 .
三、解答题
8.如图,3架飞机P,Q,R保持相对位置不变飞行,分别写出它们的坐标.30s后,飞机P飞到P,位置,问:飞机Q,R飞到了什么位置?分别写出这3架飞机新位置的坐标.
9.如图:①写出A,B,C三点的坐标:A( ),B( ),C( ).
②若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A,,B,,C,,并依次连接这三个点,所得的△A,B,C,与原△ABC有怎样的位置关系?
③在②的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点A″,B″,C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
10.如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为 (-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ,△ABC的周长是 (结果保留根号);
(3)画出△ABC以点C为旋转中心、旋转180°后的△A,B,C,连结AB,和A,B,说出四边形ABA,B,是何特殊四访形.
参考答案:
【课前热身】
1.D 2.C 3.B 4.8 5.120米 6.(0,O)
【澡堂讲练】
典型例题1 ∵P(x,y)在第四象限 ∴x>0,y<0 ∵|x|=3,|y|=5 ∴x=3,y=-5 ∴P(3,-5)
巩固练习 1由,m+1=0得m=-1 ∴P(2,0)
典型例题2(1)A,(-1,-3)(2)作A,,连结A,B交x轴于P 最小值为A,B==4
巩固练习 2存在,若顶角顶点为P,则P(0,0) 若顶角顶点为A,则P(1-,0)或(+1,0) 若顶角顶点为B,则P(-1,0)
典型例题3 (1)如图,建立坐标系,得B(2,1)
(2)如图
(3)S△A,B,C,=·4·8=16
巩固练习3如图,B,(5,O),C,(3,4)
典型例题4(1)如图,B,(0,-6) (2)D(3,3)或D(-5,-3)或D(-7,3)
巩固练习4 C
【跟踪演练】
1.D 2.B 3.D 4.A 5.4 6.-2 (2,-3)7.(4,4)8.解:Q,(2,3) R,(4,1) P,(4,3),9.①3,4 1,2 5,1 ②关于x轴对称③关于原点O对称 10.(1)略 (2)(-1,1) 2+2 (3)矩形(或长方形)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
