有理数的运算

(共18张PPT)
有理数的运算
第二章
有理数的加法法则
2 +3= 5
(-2) +3= 1
2 +（-3）= -1
(-2) +（-3）=-5
同号两数相加，取加数的符号，并把绝对值相加。
异号
同号
异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。
互为相反数的 两个数相加得零
一个数与零相加，仍得这个数。
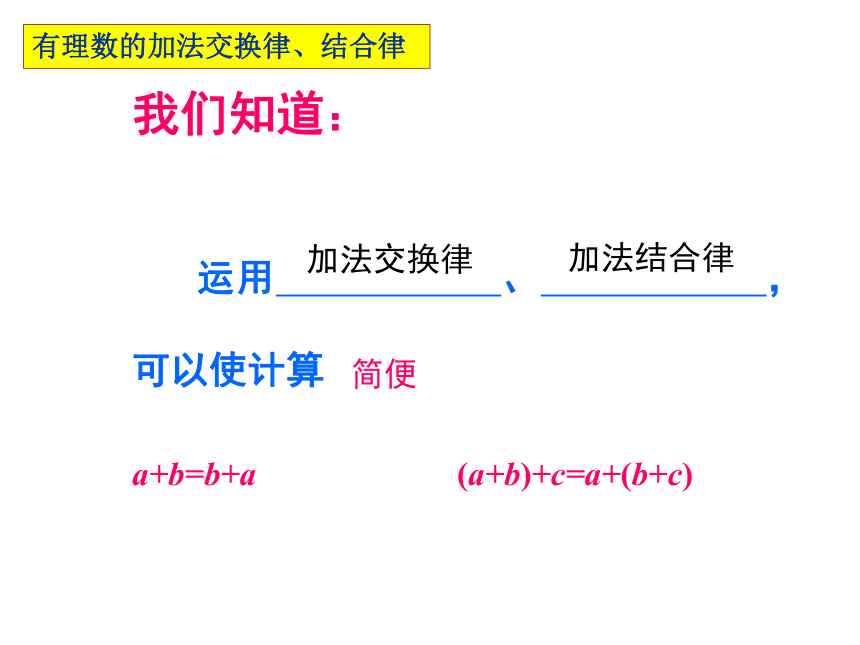
我们知道：
运用 、 ， 可以使计算
a+b=b+a (a+b)+c=a+(b+c)
加法交换律
加法结合律
简便
有理数的加法交换律、结合律
请同学们计算：
＋
＋
＋
这个你会吗
－
＋
－
－
＝
－
＋
－
－
＝
＝
0
－
10
－10
（
）
（
）
+
（1）交换加数的位置时，一定要连同加数前的_________一起交换；
（2）若第一项是省略正号的正数，交换后必须 ；
正负号
补上“+”号
注意：
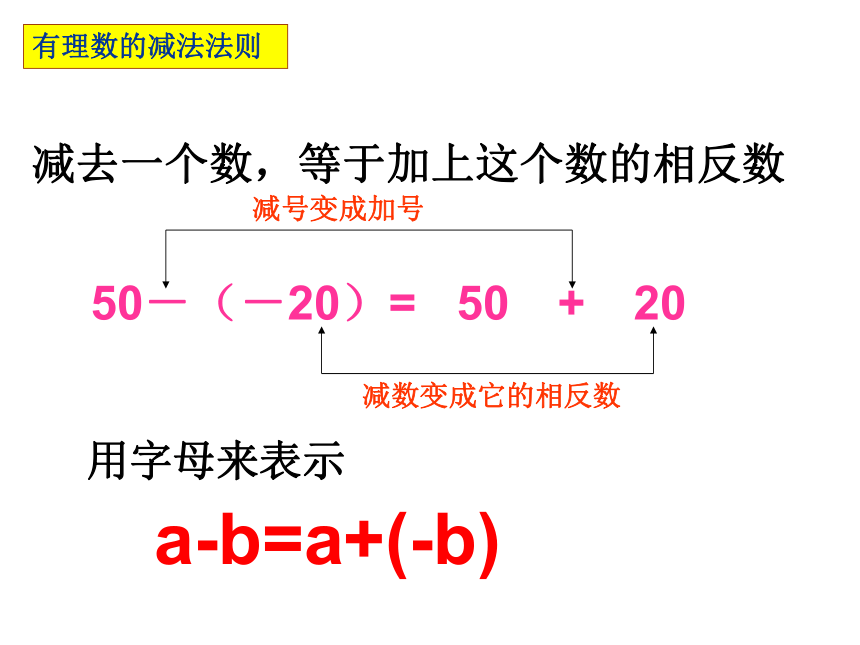
减去一个数，等于加上这个数的相反数
50－（－20）= 50　+　20
减号变成加号
减数变成它的相反数
用字母来表示
a-b=a+(-b)
有理数的减法法则
(互为相反数的加数先加)；
(能凑整的则凑整)；
(分母相同或便于通分相加)；
(符号相同的相加)；
怎样使运算简便
(1)
(2)
(3)
(4)
有理数的乘法法则
2 ×3= 6
(-2) ×3= -6
2 ×（-3）= -6
(-2) ×（-3）=6
两个有理数相乘，
同号得正，异号得负，
并把绝对值相乘。
任何数与零相乘，积为零。
异号
同号
异号
同号
两个数相
相乘，交换因数的位置，积不变
乘法交换律：
ab=ba
有理数的乘法交换律、结合律
乘法结合律：
(ab)c=a(bc)
注：若两个有理数的乘积等于1，
就称这两个有理数互为倒数。
有理数的除法法则
6 ÷3= 2
(-6) ÷3= -2
6 ÷（-3）= -2
(-6) ÷（-3）=2
两个有理数相除，
同号得正，异号得负，
并把绝对值相除。
零除以任何一个不等于零的数，
商为零。
异号
同号
异号
同号
除以一个不等于零的数，
等于乘以这个数的倒数。
有理数的除法转化为乘法
有理数的乘方
求n个相同因数a的积的运算叫做乘方，乘方的结果叫做幂，a叫做底数，n叫做指数，an读作a的n次幂（或a的n次方）。
底数
指数
幂
⑴负数的乘方，在书写时一定要_____________ _______________分数的乘方，在书 写时一定要 。
(2) 正数的任何次幂都是 ；负数的奇次幂是 ，负数的偶次幂是 。
把整个负数（连同
把整个分数用小括号括起来
正数
负数
正数
符号）用小括号括起来
40000=___________
6000000=________________
一千三百万=______________
6 ×106
1.3 ×107
把一个数表示成a（1≤a<10)与10的幂相乘的形式，叫做科学记数法。
4 ×104
科学计数法
有理数混合运算的法则
例　计算：
乘方
乘除
加减
括号里的运算
北京市某高科技蔬菜园区通过高新技术，培育出20株高产番茄树，其中最大的一株高达2米，树冠枝条面积达25平方米,结有番茄15000个左右。
准确数：与实际完全相符的数。如：20
近似数：与实际接近的数。如：2、25、15000
有效数字
由四舍五入得到的近似数，从左边第一个不是零的数字起，到末位数字为止的所有数字，都叫做这个数的有效数字。
如：3.3有 个有效数字；
3.30呢？
0.0303呢？
3.2×105呢？
2个
3个
3个
2个