2020-2021学年浙教版七年级上册第六章相交线专题培优(Word版,附图片答案)
文档属性
| 名称 | 2020-2021学年浙教版七年级上册第六章相交线专题培优(Word版,附图片答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览


文档简介
2020-2021学年浙教版七年级上册第六章相交线专题培优
班级
姓名
学号
基础巩固
1.在一个平面上任意画3条直线,最多可以把平面分成的部分数是( ).
A.4
B.6
C.7
D.8
2.下列说法中,正确的是( ).
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线相交
D.同一平面内,过一点有且只有一条直线与已知直线垂直
3.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,∠MON
=
90°.若∠MOC
=
35°,则∠BON的度数为( ).
A.35°
B.45°
C.55°
D.64°
4.如图所示,点P为直线l外一点,点A,B,C在直线l上,且PB⊥l.有下列说法:①PA,PB,PC三条线段中,PB最短;②线段PB的长叫做点P到直线l的距离;③线段AB的长是点A到PB的距离;④线段AC的长是点A到PC的距离.其中正确的是( ).
A.①②③
B.①②④
C.①③④
D.②③④
5.如图所示,直线AB,CD,EF交于点O,则∠1
+
∠2
+
∠3
=
_________
.
6.两条直线相交所成的四个角中,如果有两个角分别是(2x
-
10)和(110
-
x)°,那么x
=
_________
.
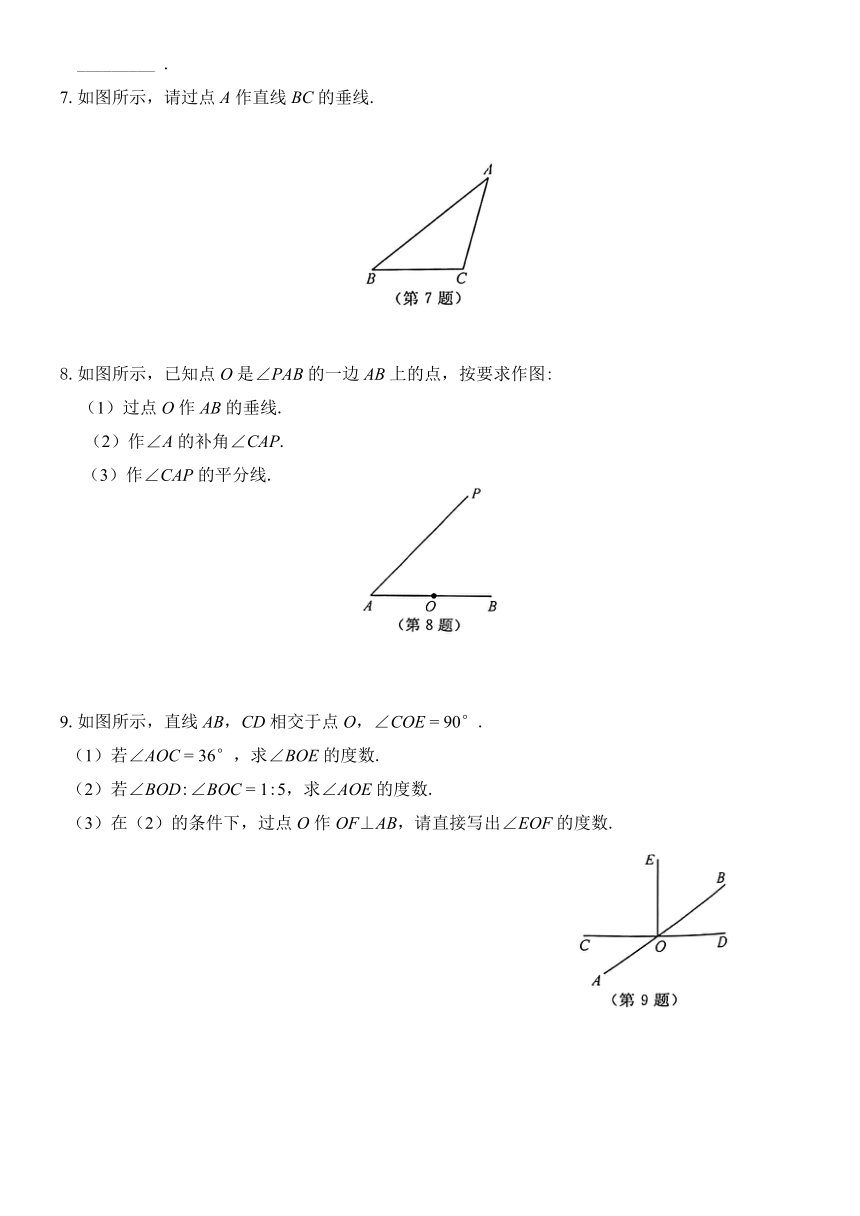
7.如图所示,请过点A作直线BC的垂线.
如图所示,已知点O是∠PAB的一边AB上的点,按要求作图:
(1)过点O作AB的垂线.
(2)作∠A的补角∠CAP.
(3)作∠CAP的平分线.
9.如图所示,直线AB,CD相交于点O,∠COE
=
90°.
(1)若∠AOC
=
36°,求∠BOE的度数.
(2)若∠BOD:∠BOC
=
1:5,求∠AOE的度数.
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
10.将一副直角三角尺按如图1所示的方式叠放,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转角(
=
∠BAD且0°
<
<
180°),使两把三角尺至少有一组对应边(所在的直线)垂直.
(1)如图2所示,当=
_________
时,BC⊥AE.
(2)请你画出两种符合要求的图形,计算出旋转角α,并用符号表示出垂直的边.
拓展提优
1.下列各图中,∠1与∠2互为对顶角的是( ).
2.如图所示,点P到直线l的距离是( ).
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
3.如图所示,直线AB与直线CD相交于点O,E是∠COB内一点,且OE⊥AB,∠AOC
=
35°,则∠EOD的度数是( ).
A.155°
B.145°
C.135°
D.125°
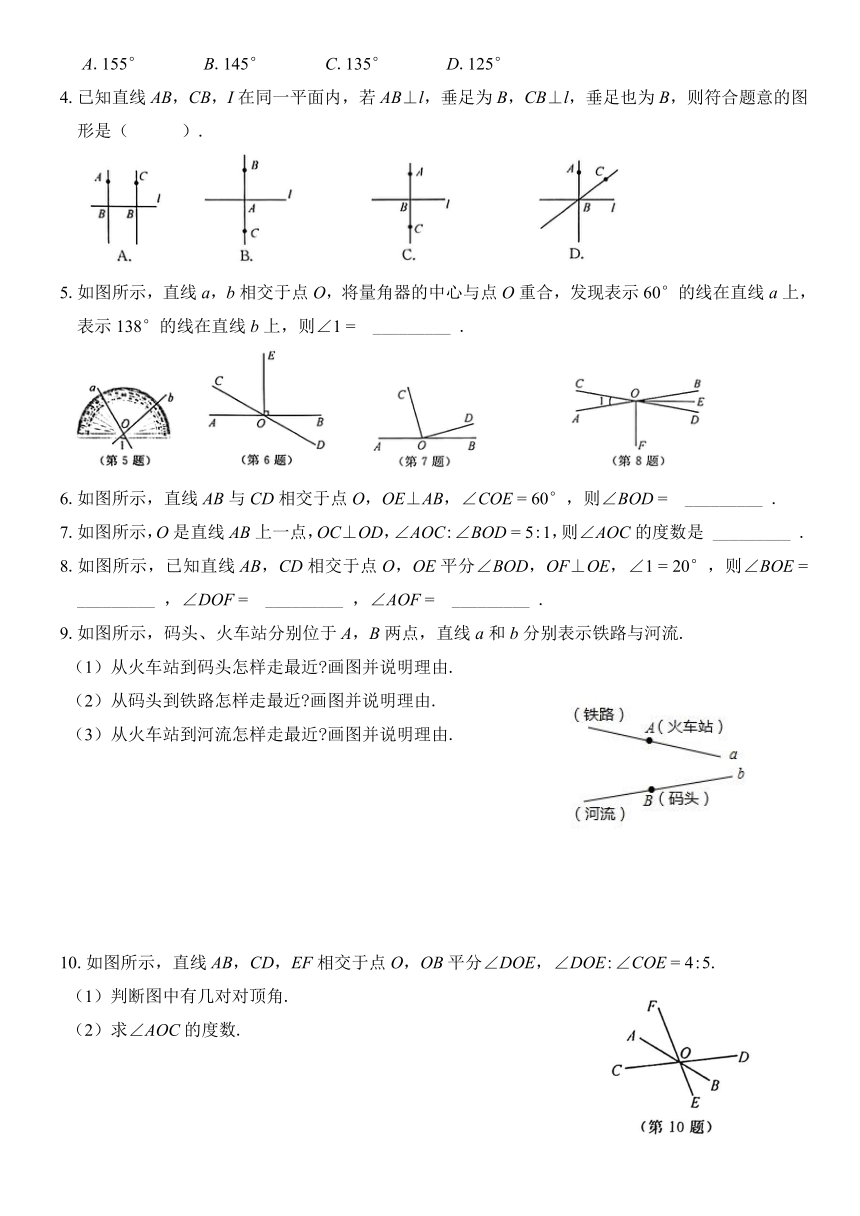
4.已知直线AB,CB,I在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形是( ).
5.如图所示,直线a,b相交于点O,将量角器的中心与点O重合,发现表示60°的线在直线a上,表示138°的线在直线b上,则∠1
=
_________
.
6.如图所示,直线AB与CD相交于点O,OE⊥AB,∠COE
=
60°,则∠BOD
=
_________
.
7.如图所示,O是直线AB上一点,OC⊥OD,∠AOC:∠BOD
=
5:1,则∠AOC的度数是
_________
.
8.如图所示,已知直线AB,CD相交于点O,OE平分∠BOD,OF⊥OE,∠1
=
20°,则∠BOE
=
_________
,∠DOF
=
_________
,∠AOF
=
_________
.
9.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由.
(2)从码头到铁路怎样走最近?画图并说明理由.
(3)从火车站到河流怎样走最近?画图并说明理由.
10.如图所示,直线AB,CD,EF相交于点O,OB平分∠DOE,∠DOE:∠COE
=
4:5.
(1)判断图中有几对对顶角.
(2)求∠AOC的度数.
11.如图所示,直线AB与CD相交于点O,∠BOE
=
∠DOF
=
90°.
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)∠COE与∠AOF相等吗?请说明理由.
(3)若∠AOC
=
∠EOF,求∠AOC的度数.
冲刺重高
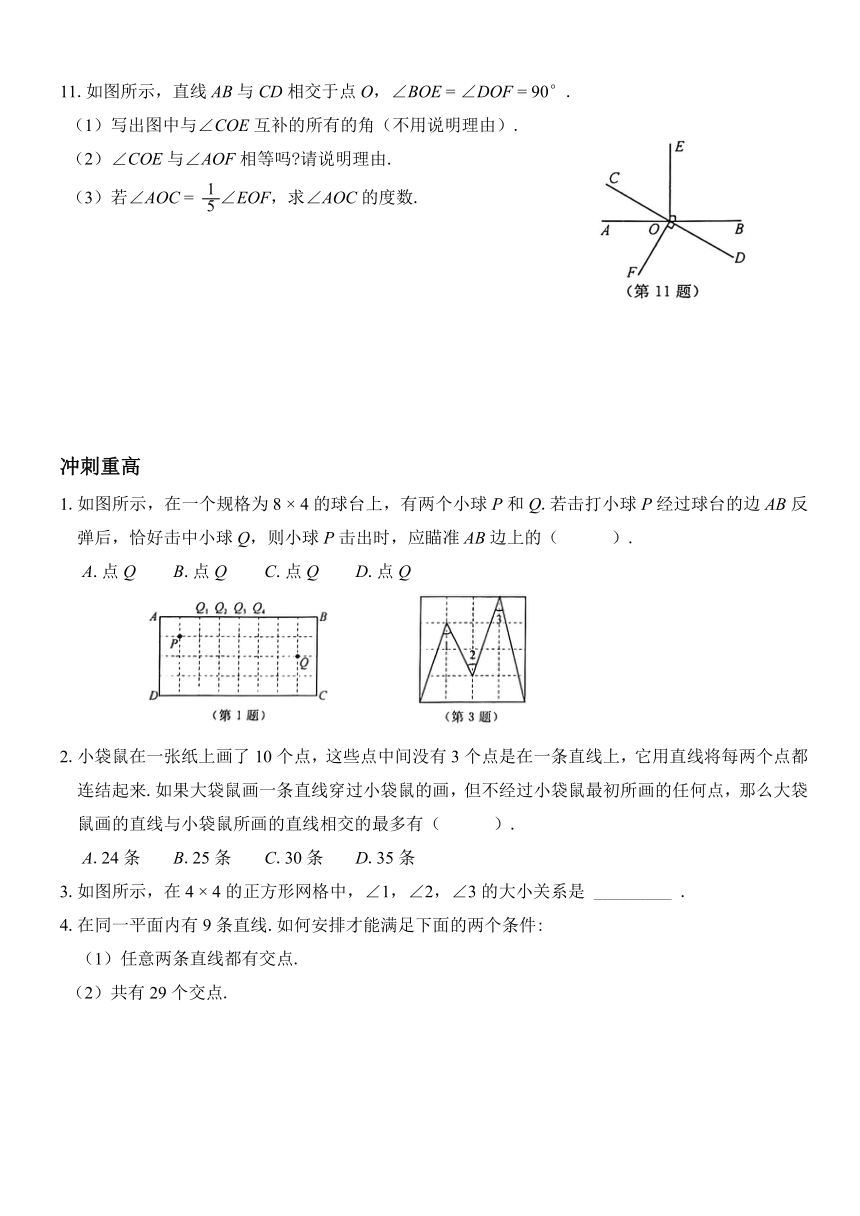
1.如图所示,在一个规格为8
×
4的球台上,有两个小球P和Q.若击打小球P经过球台的边AB反弹后,恰好击中小球Q,则小球P击出时,应瞄准AB边上的( ).
A.点Q
B.点Q
C.点Q
D.点Q
2.小袋鼠在一张纸上画了10个点,这些点中间没有3个点是在一条直线上,它用直线将每两个点都连结起来.如果大袋鼠画一条直线穿过小袋鼠的画,但不经过小袋鼠最初所画的任何点,那么大袋鼠画的直线与小袋鼠所画的直线相交的最多有( ).
A.24条
B.25条
C.30条
D.35条
3.如图所示,在4
×
4的正方形网格中,∠1,∠2,∠3的大小关系是
_________
.
4.在同一平面内有9条直线.如何安排才能满足下面的两个条件:
(1)任意两条直线都有交点.
(2)共有29个交点.
5.如图1所示,点O为直线AB上一点,过点O作射线OC,使∠BOC
=
110°.将一直角三角尺的直角顶点放在点O处(∠OMN
=
30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图1中的三角尺绕点O以5°/s的速度逆时针旋转一周,在旋转的过程中,第t(s)时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠CON的数量关系,并说明理由.
班级
姓名
学号
基础巩固
1.在一个平面上任意画3条直线,最多可以把平面分成的部分数是( ).
A.4
B.6
C.7
D.8
2.下列说法中,正确的是( ).
A.两点之间的距离是两点间的线段
B.与同一条直线垂直的两条直线也垂直
C.同一平面内,过一点有且只有一条直线与已知直线相交
D.同一平面内,过一点有且只有一条直线与已知直线垂直
3.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,∠MON
=
90°.若∠MOC
=
35°,则∠BON的度数为( ).
A.35°
B.45°
C.55°
D.64°
4.如图所示,点P为直线l外一点,点A,B,C在直线l上,且PB⊥l.有下列说法:①PA,PB,PC三条线段中,PB最短;②线段PB的长叫做点P到直线l的距离;③线段AB的长是点A到PB的距离;④线段AC的长是点A到PC的距离.其中正确的是( ).
A.①②③
B.①②④
C.①③④
D.②③④
5.如图所示,直线AB,CD,EF交于点O,则∠1
+
∠2
+
∠3
=
_________
.
6.两条直线相交所成的四个角中,如果有两个角分别是(2x
-
10)和(110
-
x)°,那么x
=
_________
.
7.如图所示,请过点A作直线BC的垂线.
如图所示,已知点O是∠PAB的一边AB上的点,按要求作图:
(1)过点O作AB的垂线.
(2)作∠A的补角∠CAP.
(3)作∠CAP的平分线.
9.如图所示,直线AB,CD相交于点O,∠COE
=
90°.
(1)若∠AOC
=
36°,求∠BOE的度数.
(2)若∠BOD:∠BOC
=
1:5,求∠AOE的度数.
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
10.将一副直角三角尺按如图1所示的方式叠放,现将含45°角的三角尺ADE固定不动,把含30°角的三角尺ABC绕顶点A顺时针旋转角(
=
∠BAD且0°
<
<
180°),使两把三角尺至少有一组对应边(所在的直线)垂直.
(1)如图2所示,当=
_________
时,BC⊥AE.
(2)请你画出两种符合要求的图形,计算出旋转角α,并用符号表示出垂直的边.
拓展提优
1.下列各图中,∠1与∠2互为对顶角的是( ).
2.如图所示,点P到直线l的距离是( ).
A.线段PA的长度
B.线段PB的长度
C.线段PC的长度
D.线段PD的长度
3.如图所示,直线AB与直线CD相交于点O,E是∠COB内一点,且OE⊥AB,∠AOC
=
35°,则∠EOD的度数是( ).
A.155°
B.145°
C.135°
D.125°
4.已知直线AB,CB,I在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形是( ).
5.如图所示,直线a,b相交于点O,将量角器的中心与点O重合,发现表示60°的线在直线a上,表示138°的线在直线b上,则∠1
=
_________
.
6.如图所示,直线AB与CD相交于点O,OE⊥AB,∠COE
=
60°,则∠BOD
=
_________
.
7.如图所示,O是直线AB上一点,OC⊥OD,∠AOC:∠BOD
=
5:1,则∠AOC的度数是
_________
.
8.如图所示,已知直线AB,CD相交于点O,OE平分∠BOD,OF⊥OE,∠1
=
20°,则∠BOE
=
_________
,∠DOF
=
_________
,∠AOF
=
_________
.
9.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近?画图并说明理由.
(2)从码头到铁路怎样走最近?画图并说明理由.
(3)从火车站到河流怎样走最近?画图并说明理由.
10.如图所示,直线AB,CD,EF相交于点O,OB平分∠DOE,∠DOE:∠COE
=
4:5.
(1)判断图中有几对对顶角.
(2)求∠AOC的度数.
11.如图所示,直线AB与CD相交于点O,∠BOE
=
∠DOF
=
90°.
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)∠COE与∠AOF相等吗?请说明理由.
(3)若∠AOC
=
∠EOF,求∠AOC的度数.
冲刺重高
1.如图所示,在一个规格为8
×
4的球台上,有两个小球P和Q.若击打小球P经过球台的边AB反弹后,恰好击中小球Q,则小球P击出时,应瞄准AB边上的( ).
A.点Q
B.点Q
C.点Q
D.点Q
2.小袋鼠在一张纸上画了10个点,这些点中间没有3个点是在一条直线上,它用直线将每两个点都连结起来.如果大袋鼠画一条直线穿过小袋鼠的画,但不经过小袋鼠最初所画的任何点,那么大袋鼠画的直线与小袋鼠所画的直线相交的最多有( ).
A.24条
B.25条
C.30条
D.35条
3.如图所示,在4
×
4的正方形网格中,∠1,∠2,∠3的大小关系是
_________
.
4.在同一平面内有9条直线.如何安排才能满足下面的两个条件:
(1)任意两条直线都有交点.
(2)共有29个交点.
5.如图1所示,点O为直线AB上一点,过点O作射线OC,使∠BOC
=
110°.将一直角三角尺的直角顶点放在点O处(∠OMN
=
30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.求∠BON的度数.
(2)将图1中的三角尺绕点O以5°/s的速度逆时针旋转一周,在旋转的过程中,第t(s)时,直线ON恰好平分锐角∠AOC,求t的值.
(3)将图1中的三角尺绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠CON的数量关系,并说明理由.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
