浙教版数学八年级上4.3坐标平面内图形的轴对称和平移(1)教学设计
文档属性
| 名称 | 浙教版数学八年级上4.3坐标平面内图形的轴对称和平移(1)教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 09:30:46 | ||
图片预览


文档简介
浙教版数学八年级上4.3坐标平面内图形的轴对称和平移(1)教学设计
课题
4.3坐标平面内图形的轴对称和平移(1)
单元
第四章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
通过生动有趣的教学活动,发展学生的合情推理能力和丰富的情感、态度,提高学生学习数学的兴趣。
能力目标
进一步培养坐标意识与数形结合的数学思想,培养学生自主探究能力和合作学习能力
知识目标
1.感受坐标平面内图形变换的坐标变换,了解关于坐标轴对称的两个点的坐标变换;?2、会求与已知点关于坐标轴对称点的坐标;利用图形变换与坐标之间的关系来作图;
重点
关于坐标轴对称的两个点之间的坐标关系。
难点
利用关于坐标轴对称的两个点之间的坐标关系,在平面直角坐标系内作轴对称图形。
学法
探究法
教法
讲授法
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
在坐标平面内,怎样通过作第一象限图案的轴对称图形,从而得到整个图形,从而得到整个图案?学完本课知识,你就知道答案
观察、思考
通过提问引入本课知识
探究发现
如图:
(1)写出点A的坐标;(2)分别作点A关于x轴,y轴的对称点,并写出它的坐标;(3)比较点A与它关于
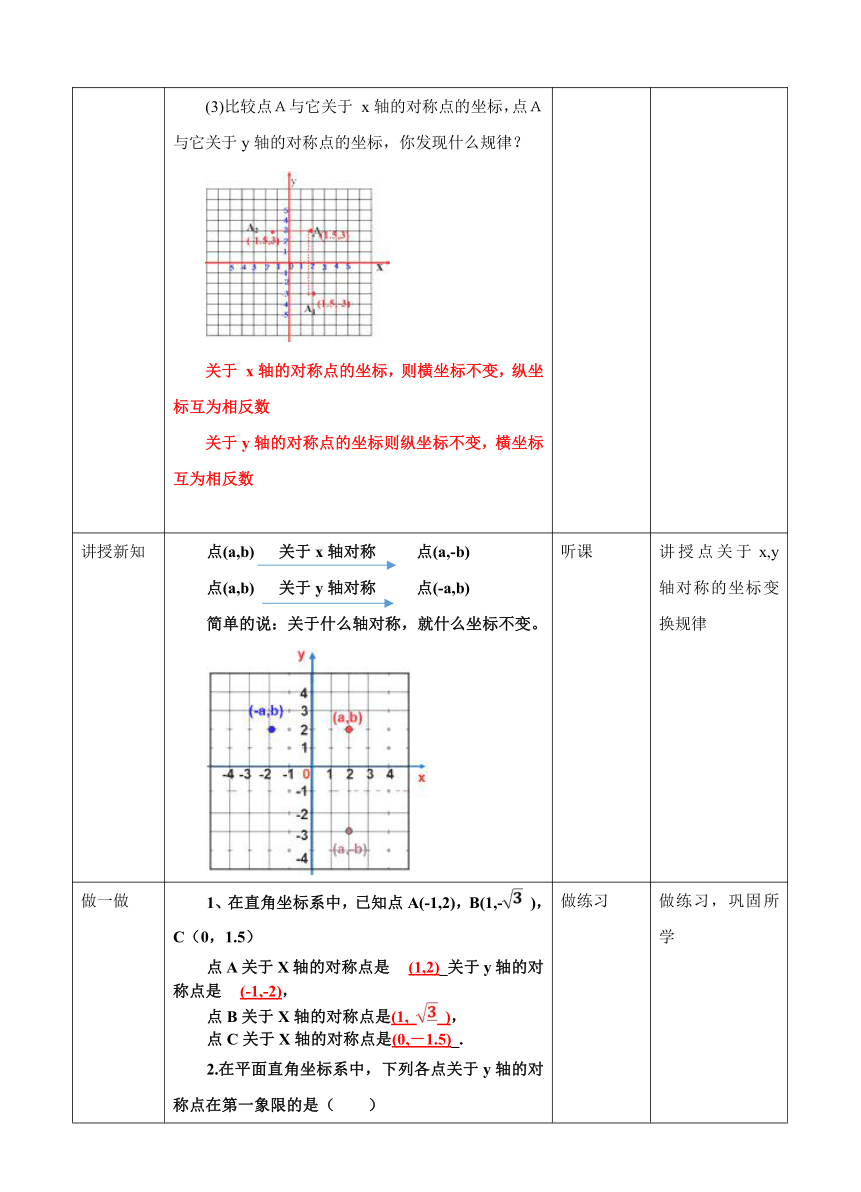
x轴的对称点的坐标,点A与它关于y轴的对称点的坐标,你发现什么规律?关于
x轴的对称点的坐标,则横坐标不变,纵坐标互为相反数关于y轴的对称点的坐标则纵坐标不变,横坐标互为相反数
观察发现
培养学生自主探究能力
讲授新知
点(a,b)
关于x轴对称
点(a,-b)点(a,b)
关于y轴对称
点(-a,b)简单的说:关于什么轴对称,就什么坐标不变。
听课
讲授点关于x,y轴对称的坐标变换规律
做一做
1、在直角坐标系中,已知点A(-1,2),B(1,-
),
C(0,1.5)点A关于X轴的对称点是
(1,2)_关于y轴的对称点是
(-1,-2),点B关于X轴的对称点是(1,
),点C关于X轴的对称点是(0,-1.5)_.2.在平面直角坐标系中,下列各点关于y轴的对称点在第一象限的是( )A.(2,1)
B.(2,-1)
C.(-2,1)
D.(-2,-1)A、(2,1)关于y轴的对称点是(-2,1),在第二象限.
B、(2,-1)关于y轴的对称点是(-2,-1),在第三象限.
C、(-2,1)关于y轴的对称点是(2,1),在第一象限.
D、(-2,-1)关于y轴的对称点是(2,-1).在第四象限.
做练习
做练习,巩固所学
例题讲解
例1
(1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标以及它们关于y轴的对称点A′,O′,B′,C′,D′,E′,F′的坐标。(2)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用线段依次将它们连接起来。解:(1)图形轮廓线上各转折点的坐标依次是:A(0,-2)
O(0,0)B(3,2)
C(2,2)
D(2,3)
E(1,3)
F(0,5)A'(0,-2)
O'(0,0)
B'(-3,2)
C'(-2,2)
D'(-2,3)
E'(-1,3)F'(0,5)(2)点A′,O′,B′,C′,D′,E′,F′及其连线如图。
听课思考
讲解例题,明白题型
即时演练
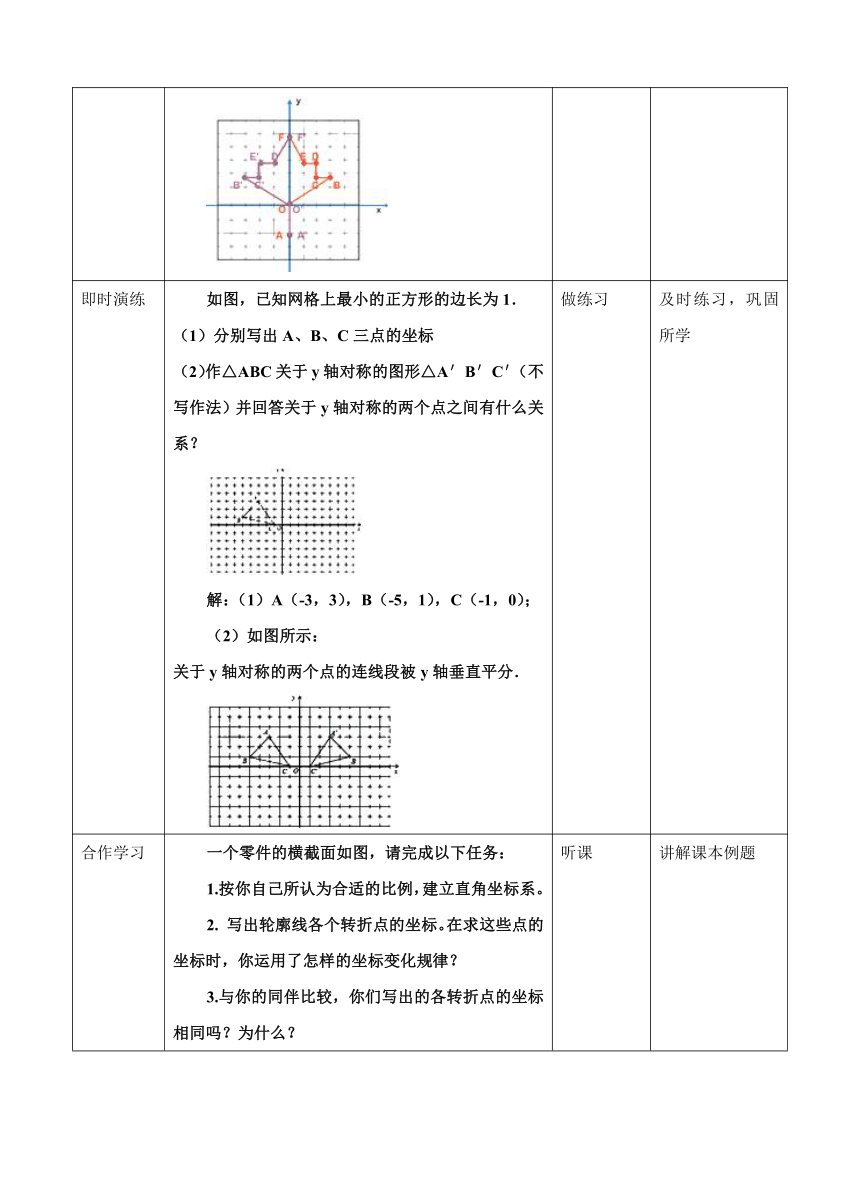
如图,已知网格上最小的正方形的边长为1.
(1)分别写出A、B、C三点的坐标
(2)作△ABC关于y轴对称的图形△A′B′C′(不写作法)并回答关于y轴对称的两个点之间有什么关系?解:(1)A(-3,3),B(-5,1),C(-1,0);(2)如图所示:
关于y轴对称的两个点的连线段被y轴垂直平分.
做练习
及时练习,巩固所学
合作学习
一个零件的横截面如图,请完成以下任务:1.按你自己所认为合适的比例,建立直角坐标系。2.
写出轮廓线各个转折点的坐标。在求这些点的坐标时,你运用了怎样的坐标变化规律?3.与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么?(1)比例尺为1:10图上尺寸如右图所示(2)比例尺为1:10,单位:cm运用了点关于x轴对称,纵坐标不变,横坐标互为相反数的坐标变换规律(3)因为选定的坐标系不同,所以每个人写出的点的坐标是不一样的
听课
讲解课本例题
即时演练
将?ABC各顶点的横坐标,纵坐标分别乘以-1,得到的图形与原图形相比有什么变化?三个顶点坐标的横坐标都乘以-1,并保持纵坐标不变,就是横坐标变成相反数.即所得到的点与原来的点关于y轴对称原来的图形以原点为中心旋转180°就是最后得到的图形
达标测评
1.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
A.0
B.-1
C.1
D.(-3)2009解:∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,
∴a=3,b=-4,
∴(a+b)2009=(3-4)2009=-1.
故选B.2.已知M(a,3)和N(4,b)关于x轴对称,则a+b的值为( )
A.1
B.-1
C.7
D.-7解:∵M(a,3)和N(4,b)关于x轴对称,
∴a=4,b=-3,
则a+b的值为:4-3=1.
故选A.3.平面直角坐标系中,点P的坐标是(-3,b)和点Q的坐标(a,-2)是关于x轴对称,则a-b=______.解:∵点P的坐标是(-3,b)和点Q的坐标(a,-2)是关于x轴对称,
∴a=-3,b=2,
∴a-b=-3-2=-5,
故答案为:-5.4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是___________.解:∵点A的坐标为(-1,4),
∴点C的坐标为(-3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).5.如图所示,作字母“M”关于y轴的轴对称图形,并写出所得图形相应各顶点的坐标.所得图形相应各顶点的坐标分别为:A′(4,0),B′(4,3),C′(2.5,0),D′(1,3),E′(1,0).
做题
通过做对应的题目,来让学生更深刻理解本节知识
应用拓展
在直角坐标系中,C(2,3),C'(﹣4,3),C''(2,1),D(﹣4,1),A(0,a),B(a,O)(a>0).
(1)结合坐标系用坐标填空.
点C与C'关于点?_________?对称;
点C与C''关于点?_________?对称;点C与D关于点?_________?对称;
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.解:(1)由图可知,点C与C‘关于点(﹣1,3)对称;
点C与C’’关于点(2,2)对称;点C与D关于点(﹣1,2)对称;
故答案为:(﹣1,3),(2,2),(﹣1,2);
(2)点C关于点(4,2)的对称点P(6,1),
△PAB的面积=(1+a)×6-
a?-×1×(6-a)=5整理得,a2﹣7a+10=0,
解得a1=2,a2=5,
所以,a的值为2或5.
思考练习
通过猜想拓展学生思维
课堂小结
这节课我们学习了:一、掌握二种变换:A(a,b)
关于x轴
A1(a,-b)A(a,b)
关于y轴
A2(-a,b)二、感受一种画法:学会用简单方法把一个轴对称图形画在直角坐标系中三、体验一种精神:学会用数形结合的思想思考问题
回忆总结
带领学生回忆本课所学
布置作业
课本P129页第1、
3、
4、
5
题
做练习
课下练习提升
板书
4.3
坐标平面内图形的轴对称和平移(1)1.A(a,b)
关于x轴
A1(a,-b)
A(a,b)
关于y轴
A2(-a,b)2.数形结合
看黑板
帮助学生梳理本课知识点
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
课题
4.3坐标平面内图形的轴对称和平移(1)
单元
第四章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
通过生动有趣的教学活动,发展学生的合情推理能力和丰富的情感、态度,提高学生学习数学的兴趣。
能力目标
进一步培养坐标意识与数形结合的数学思想,培养学生自主探究能力和合作学习能力
知识目标
1.感受坐标平面内图形变换的坐标变换,了解关于坐标轴对称的两个点的坐标变换;?2、会求与已知点关于坐标轴对称点的坐标;利用图形变换与坐标之间的关系来作图;
重点
关于坐标轴对称的两个点之间的坐标关系。
难点
利用关于坐标轴对称的两个点之间的坐标关系,在平面直角坐标系内作轴对称图形。
学法
探究法
教法
讲授法
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
在坐标平面内,怎样通过作第一象限图案的轴对称图形,从而得到整个图形,从而得到整个图案?学完本课知识,你就知道答案
观察、思考
通过提问引入本课知识
探究发现
如图:
(1)写出点A的坐标;(2)分别作点A关于x轴,y轴的对称点,并写出它的坐标;(3)比较点A与它关于
x轴的对称点的坐标,点A与它关于y轴的对称点的坐标,你发现什么规律?关于
x轴的对称点的坐标,则横坐标不变,纵坐标互为相反数关于y轴的对称点的坐标则纵坐标不变,横坐标互为相反数
观察发现
培养学生自主探究能力
讲授新知
点(a,b)
关于x轴对称
点(a,-b)点(a,b)
关于y轴对称
点(-a,b)简单的说:关于什么轴对称,就什么坐标不变。
听课
讲授点关于x,y轴对称的坐标变换规律
做一做
1、在直角坐标系中,已知点A(-1,2),B(1,-
),
C(0,1.5)点A关于X轴的对称点是
(1,2)_关于y轴的对称点是
(-1,-2),点B关于X轴的对称点是(1,
),点C关于X轴的对称点是(0,-1.5)_.2.在平面直角坐标系中,下列各点关于y轴的对称点在第一象限的是( )A.(2,1)
B.(2,-1)
C.(-2,1)
D.(-2,-1)A、(2,1)关于y轴的对称点是(-2,1),在第二象限.
B、(2,-1)关于y轴的对称点是(-2,-1),在第三象限.
C、(-2,1)关于y轴的对称点是(2,1),在第一象限.
D、(-2,-1)关于y轴的对称点是(2,-1).在第四象限.
做练习
做练习,巩固所学
例题讲解
例1
(1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标以及它们关于y轴的对称点A′,O′,B′,C′,D′,E′,F′的坐标。(2)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用线段依次将它们连接起来。解:(1)图形轮廓线上各转折点的坐标依次是:A(0,-2)
O(0,0)B(3,2)
C(2,2)
D(2,3)
E(1,3)
F(0,5)A'(0,-2)
O'(0,0)
B'(-3,2)
C'(-2,2)
D'(-2,3)
E'(-1,3)F'(0,5)(2)点A′,O′,B′,C′,D′,E′,F′及其连线如图。
听课思考
讲解例题,明白题型
即时演练
如图,已知网格上最小的正方形的边长为1.
(1)分别写出A、B、C三点的坐标
(2)作△ABC关于y轴对称的图形△A′B′C′(不写作法)并回答关于y轴对称的两个点之间有什么关系?解:(1)A(-3,3),B(-5,1),C(-1,0);(2)如图所示:
关于y轴对称的两个点的连线段被y轴垂直平分.
做练习
及时练习,巩固所学
合作学习
一个零件的横截面如图,请完成以下任务:1.按你自己所认为合适的比例,建立直角坐标系。2.
写出轮廓线各个转折点的坐标。在求这些点的坐标时,你运用了怎样的坐标变化规律?3.与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么?(1)比例尺为1:10图上尺寸如右图所示(2)比例尺为1:10,单位:cm运用了点关于x轴对称,纵坐标不变,横坐标互为相反数的坐标变换规律(3)因为选定的坐标系不同,所以每个人写出的点的坐标是不一样的
听课
讲解课本例题
即时演练
将?ABC各顶点的横坐标,纵坐标分别乘以-1,得到的图形与原图形相比有什么变化?三个顶点坐标的横坐标都乘以-1,并保持纵坐标不变,就是横坐标变成相反数.即所得到的点与原来的点关于y轴对称原来的图形以原点为中心旋转180°就是最后得到的图形
达标测评
1.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
A.0
B.-1
C.1
D.(-3)2009解:∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,
∴a=3,b=-4,
∴(a+b)2009=(3-4)2009=-1.
故选B.2.已知M(a,3)和N(4,b)关于x轴对称,则a+b的值为( )
A.1
B.-1
C.7
D.-7解:∵M(a,3)和N(4,b)关于x轴对称,
∴a=4,b=-3,
则a+b的值为:4-3=1.
故选A.3.平面直角坐标系中,点P的坐标是(-3,b)和点Q的坐标(a,-2)是关于x轴对称,则a-b=______.解:∵点P的坐标是(-3,b)和点Q的坐标(a,-2)是关于x轴对称,
∴a=-3,b=2,
∴a-b=-3-2=-5,
故答案为:-5.4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是___________.解:∵点A的坐标为(-1,4),
∴点C的坐标为(-3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).5.如图所示,作字母“M”关于y轴的轴对称图形,并写出所得图形相应各顶点的坐标.所得图形相应各顶点的坐标分别为:A′(4,0),B′(4,3),C′(2.5,0),D′(1,3),E′(1,0).
做题
通过做对应的题目,来让学生更深刻理解本节知识
应用拓展
在直角坐标系中,C(2,3),C'(﹣4,3),C''(2,1),D(﹣4,1),A(0,a),B(a,O)(a>0).
(1)结合坐标系用坐标填空.
点C与C'关于点?_________?对称;
点C与C''关于点?_________?对称;点C与D关于点?_________?对称;
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求a值.解:(1)由图可知,点C与C‘关于点(﹣1,3)对称;
点C与C’’关于点(2,2)对称;点C与D关于点(﹣1,2)对称;
故答案为:(﹣1,3),(2,2),(﹣1,2);
(2)点C关于点(4,2)的对称点P(6,1),
△PAB的面积=(1+a)×6-
a?-×1×(6-a)=5整理得,a2﹣7a+10=0,
解得a1=2,a2=5,
所以,a的值为2或5.
思考练习
通过猜想拓展学生思维
课堂小结
这节课我们学习了:一、掌握二种变换:A(a,b)
关于x轴
A1(a,-b)A(a,b)
关于y轴
A2(-a,b)二、感受一种画法:学会用简单方法把一个轴对称图形画在直角坐标系中三、体验一种精神:学会用数形结合的思想思考问题
回忆总结
带领学生回忆本课所学
布置作业
课本P129页第1、
3、
4、
5
题
做练习
课下练习提升
板书
4.3
坐标平面内图形的轴对称和平移(1)1.A(a,b)
关于x轴
A1(a,-b)
A(a,b)
关于y轴
A2(-a,b)2.数形结合
看黑板
帮助学生梳理本课知识点
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
