浙教版数学八年级上册 3.1认识不等式教学设计
文档属性
| 名称 | 浙教版数学八年级上册 3.1认识不等式教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 174.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 09:32:15 | ||
图片预览



文档简介
浙教版数学八年级上3.1认识不等式教学设计
课题
认识不等式
单元
第三章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
感受不等式在生活中的应用,感受数学的乐趣。
能力目标
在学习过程中培养学生自主思考,勇于探究和合作学习的能力
知识目标
1.掌握不等式的定义2.掌握用数轴表示不等式3.能利用不等式解决实际问题
重点
用数轴表示不等式
难点
利用数轴表达不等式
学法
探究法
教法
讲授法
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
双润溪水库的水位在15-25m(包括15m,25m)时,发电机能正常工作,设水库水位为x(m)。你能用关于x的式子表示水位的高度吗?15≤x≤25
听课
用生活实例引入本课内容,吸引学生注意力
合作学习
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示?(1)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系?V
≤
40 (2)根据科学家测定,太阳表面的温度不低于6000℃。设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?
t
≥
6000(3)天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x
>5
(4)小明与小聪玩跷跷板,大家都不用力时,跷跷板左低右高.小明的身体质量为p(kg),小聪的身体质量为q(kg),书包的质量为2kg,
怎样表示p
、q之间的关系?
p
<q
+2
(5)要使代数式
有意义,
x的值与3之间有什么关系?x≠
3
观察
回答问题
从学生熟悉的事物引入本课知识
讲授新课
像V≤40,t≥6000,3x>5,q<p+2
,x≠3这样,用“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子,叫做不等式。这些用来连接的符号统称不等号
听课
讲授不等式的定义
即时演练
选用适当的不等号填空:-x2______0,-9______|a+8|,
(a-1)2______-2(a-1)2
做练习
及时做题,巩固所学
例题讲解
例1.根据下列数量关系列不等式:(1)a是正数(2)y的2倍与6的和比1小(3)x?减去10不大于10(4)设a,b,
c为一个三角形的三条边,两边之和大于第三边。解:(1)a是正数,a>0(2)
y的2倍与6的和比1小,2y+6<1(3)x?减去10不大于10,x?-10≤10(4)三角形两边之和大于第三边,a+b>c,a+c>b,b+c>a
听课
讲解例题,熟悉题型
小结归纳
列不等式的步骤:(1)根据条件中的关系语确定不等式两边的代数式(2)根据条件中的关系选择合适的不等号
听课思考
总结方法
即时演练
用适当的符号表示下列关系:
(1)x2是非负数;
(2)x的相反数与1的差不小于2;
(3)x与17的和比它的5倍小。
解:(1)中的非负数就是大于等于零,即“≥”;x?≥0
(2)不小于就是大于等于;
-x-1≥2
(3)中关键词是“小”等。
x+17<5x
做练习
及时练习,巩固所学
做一做
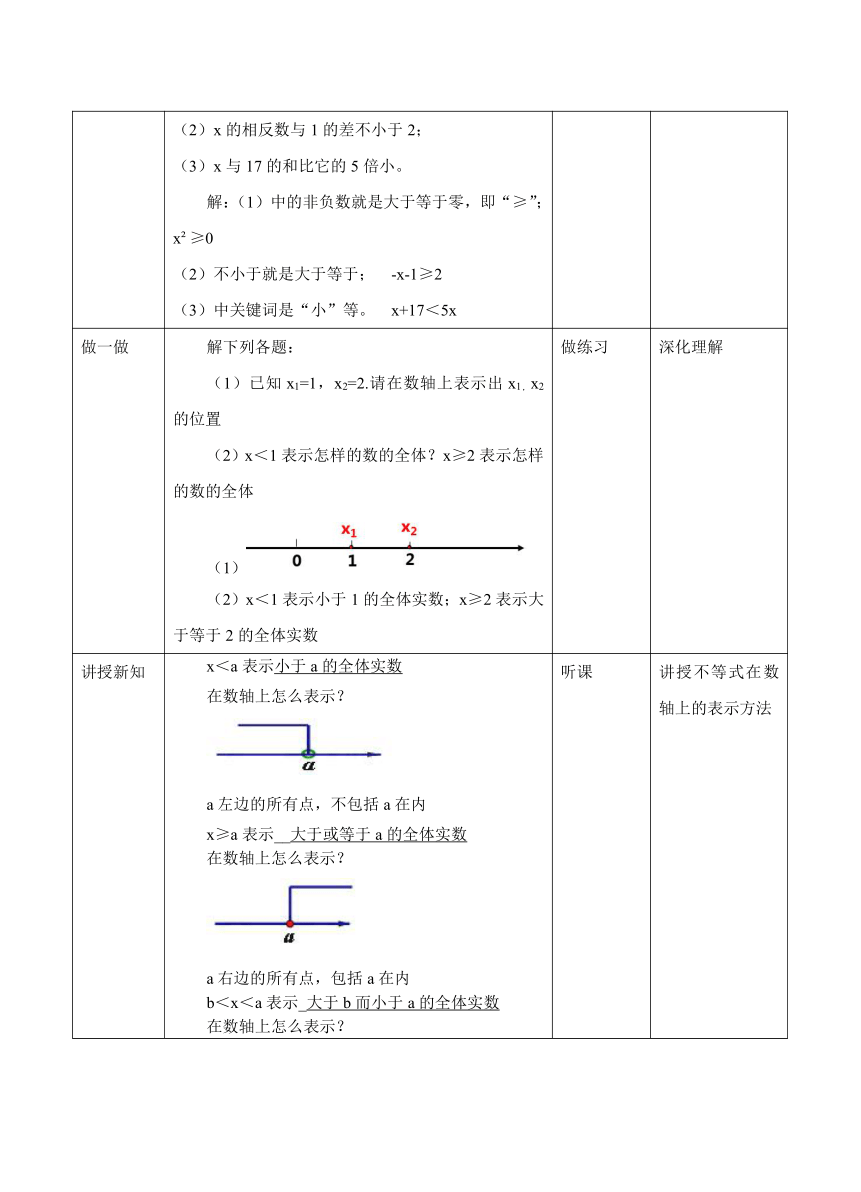
解下列各题:(1)已知x1=1,x2=2.请在数轴上表示出x1,x2的位置(2)x<1表示怎样的数的全体?x≥2表示怎样的数的全体(1)(2)x<1表示小于1的全体实数;x≥2表示大于等于2的全体实数
做练习
深化理解
讲授新知
x<a表示小于a的全体实数在数轴上怎么表示?a左边的所有点,不包括a在内x≥a表示__大于或等于a的全体实数在数轴上怎么表示?a右边的所有点,包括a在内b<x<a表示_大于b而小于a的全体实数在数轴上怎么表示?b右边,a左边的所有点,不包括a,b在内类似地,你能在数轴上分别标出x>a,
x≤a和b≤x<a(b<a)对应的点吗?x>a
x≤a
b≤x<a
在数轴上表示不等式的步骤:备好数轴找准点分清空实定方向无等号
---空心有等号---实心
大于--向右
小于--向左
听课
讲授不等式在数轴上的表示方法
例题讲解
例2:一座小水电站的水库水位在12~20m(包括12m,20m)时,发电机能正常工作。设水库水位为x(m).(1)用不等式表示发电机正常工作水位范围,并表示在数轴上;(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。解:(1)正常工作范围
12≤x≤20,在数轴上表示为:(2)把x1=8,x2=10,x3=15,x4=19表示在数轴上,如图:显然,
x3,x4满足不等式12≤x≤20
,而x1,x2不满足,
也就是说,
当水位在15m,19m时,发电机能正常工作;当水位在8m,10m时,发电机不能正常工作。
听课思考
讲解例题,明白题型
即时演练
小李与小王决定把每月省下的零用钱存起来.小李原来存了80元,小王原来存了54元.从这个月开始,小李计划每月存16元,小王计划每月存20元.
(1)设x个月后小王的存款数超过小李,试根据题意列出不等式;
(2)6个月后,小王的存款数是否已超过小李?7个月后呢?解:(1)54+20x>80+16x;
(2)6个月后,小王的存款数是54+20×6=174,小李的存款数是80+16×6=176,所以小王的存款数没有超过小李;
7个月后,小王的存款数是54+20×7=194,小李的存款数是80+16×7=192,所以小王的存款数超过了小李.
练习
及时练习,巩固所学
达标测评
1.下面列出的不等式中,正确的是( )A.a不是负数,可表示成a>0B.x不大于3,可表示成x<3C.m与4的差是负数,可表示成m-4<0D.x与2的和是非负数,可表示成x+2>0A、a不是负数,可表示成a≥0,故本选项错误;
B、x不大于3,可表示成x≤3,故本选项错误;
C、m与4的差是负数,可表示成m-4<0,故本选项正确;
D、x与2的和是非负数,可表示成x+2≥0,故本选项错误.
故选C.2.已知有理数m,n的位置在数轴上如图所示,用不等号填空.(1)n-m______0;(2)m+n______0;(3)m-n______0;(4)n+1______0;(5)m?n______0;
(6)m+1______0.解:(1)因为n<0,m>0,所以n-m<0;
(2)因为n<0、m>0,且|n|>1、|m|<1,所以m+n<0;
(3)因为n<0,m>0,所以n-m>0;
(4)因为n<0,|n|>1,所以n+1<0;
(5)因为n<0,m>0,所以m?n<0;
(6)因为0<m<1,所以m+1>0.
做题
通过做对应的题目,来让学生更深刻理解本节知识
课堂小结
这节课我们学习了:1.不等式主要用来刻画现实生活中的不等关系2.在列不等式时,关键要确定不等号的方向,其次要确定等号能否取到3.在数轴上表示不等式时,一要选取合适的单位长度,二要确定不等式的方向,三要注意空心点与实心点之间的区别。
回忆总结
带领学生回忆本课所学
布置作业
课本P93页第1、
5、
6
题
做练习
课下练习提升
板书
3.1
认识不等式1.不等式的定义:用不等号连接的数学式子2.不等式在数轴上的表示3.应用
看黑板
帮助学生梳理本课知识点
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
8
页)
课题
认识不等式
单元
第三章
学科
数学
年级
八年级
学习目标
情感态度和价值观目标
感受不等式在生活中的应用,感受数学的乐趣。
能力目标
在学习过程中培养学生自主思考,勇于探究和合作学习的能力
知识目标
1.掌握不等式的定义2.掌握用数轴表示不等式3.能利用不等式解决实际问题
重点
用数轴表示不等式
难点
利用数轴表达不等式
学法
探究法
教法
讲授法
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
双润溪水库的水位在15-25m(包括15m,25m)时,发电机能正常工作,设水库水位为x(m)。你能用关于x的式子表示水位的高度吗?15≤x≤25
听课
用生活实例引入本课内容,吸引学生注意力
合作学习
下列问题中的数量关系能用等式表示吗?若不能,应该用怎样的式子来表示?(1)下图为公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(km/h)表示汽车的速度,怎样表示v和40之间的关系?V
≤
40 (2)根据科学家测定,太阳表面的温度不低于6000℃。设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?
t
≥
6000(3)天平左盘放3个乒乓球,右盘放5克砝码,天平倾斜,设每个乒乓球的质量为x(g),怎样表示x与5之间的关系?
3x
>5
(4)小明与小聪玩跷跷板,大家都不用力时,跷跷板左低右高.小明的身体质量为p(kg),小聪的身体质量为q(kg),书包的质量为2kg,
怎样表示p
、q之间的关系?
p
<q
+2
(5)要使代数式
有意义,
x的值与3之间有什么关系?x≠
3
观察
回答问题
从学生熟悉的事物引入本课知识
讲授新课
像V≤40,t≥6000,3x>5,q<p+2
,x≠3这样,用“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子,叫做不等式。这些用来连接的符号统称不等号
听课
讲授不等式的定义
即时演练
选用适当的不等号填空:-x2______0,-9______|a+8|,
(a-1)2______-2(a-1)2
做练习
及时做题,巩固所学
例题讲解
例1.根据下列数量关系列不等式:(1)a是正数(2)y的2倍与6的和比1小(3)x?减去10不大于10(4)设a,b,
c为一个三角形的三条边,两边之和大于第三边。解:(1)a是正数,a>0(2)
y的2倍与6的和比1小,2y+6<1(3)x?减去10不大于10,x?-10≤10(4)三角形两边之和大于第三边,a+b>c,a+c>b,b+c>a
听课
讲解例题,熟悉题型
小结归纳
列不等式的步骤:(1)根据条件中的关系语确定不等式两边的代数式(2)根据条件中的关系选择合适的不等号
听课思考
总结方法
即时演练
用适当的符号表示下列关系:
(1)x2是非负数;
(2)x的相反数与1的差不小于2;
(3)x与17的和比它的5倍小。
解:(1)中的非负数就是大于等于零,即“≥”;x?≥0
(2)不小于就是大于等于;
-x-1≥2
(3)中关键词是“小”等。
x+17<5x
做练习
及时练习,巩固所学
做一做
解下列各题:(1)已知x1=1,x2=2.请在数轴上表示出x1,x2的位置(2)x<1表示怎样的数的全体?x≥2表示怎样的数的全体(1)(2)x<1表示小于1的全体实数;x≥2表示大于等于2的全体实数
做练习
深化理解
讲授新知
x<a表示小于a的全体实数在数轴上怎么表示?a左边的所有点,不包括a在内x≥a表示__大于或等于a的全体实数在数轴上怎么表示?a右边的所有点,包括a在内b<x<a表示_大于b而小于a的全体实数在数轴上怎么表示?b右边,a左边的所有点,不包括a,b在内类似地,你能在数轴上分别标出x>a,
x≤a和b≤x<a(b<a)对应的点吗?x>a
x≤a
b≤x<a
在数轴上表示不等式的步骤:备好数轴找准点分清空实定方向无等号
---空心有等号---实心
大于--向右
小于--向左
听课
讲授不等式在数轴上的表示方法
例题讲解
例2:一座小水电站的水库水位在12~20m(包括12m,20m)时,发电机能正常工作。设水库水位为x(m).(1)用不等式表示发电机正常工作水位范围,并表示在数轴上;(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。解:(1)正常工作范围
12≤x≤20,在数轴上表示为:(2)把x1=8,x2=10,x3=15,x4=19表示在数轴上,如图:显然,
x3,x4满足不等式12≤x≤20
,而x1,x2不满足,
也就是说,
当水位在15m,19m时,发电机能正常工作;当水位在8m,10m时,发电机不能正常工作。
听课思考
讲解例题,明白题型
即时演练
小李与小王决定把每月省下的零用钱存起来.小李原来存了80元,小王原来存了54元.从这个月开始,小李计划每月存16元,小王计划每月存20元.
(1)设x个月后小王的存款数超过小李,试根据题意列出不等式;
(2)6个月后,小王的存款数是否已超过小李?7个月后呢?解:(1)54+20x>80+16x;
(2)6个月后,小王的存款数是54+20×6=174,小李的存款数是80+16×6=176,所以小王的存款数没有超过小李;
7个月后,小王的存款数是54+20×7=194,小李的存款数是80+16×7=192,所以小王的存款数超过了小李.
练习
及时练习,巩固所学
达标测评
1.下面列出的不等式中,正确的是( )A.a不是负数,可表示成a>0B.x不大于3,可表示成x<3C.m与4的差是负数,可表示成m-4<0D.x与2的和是非负数,可表示成x+2>0A、a不是负数,可表示成a≥0,故本选项错误;
B、x不大于3,可表示成x≤3,故本选项错误;
C、m与4的差是负数,可表示成m-4<0,故本选项正确;
D、x与2的和是非负数,可表示成x+2≥0,故本选项错误.
故选C.2.已知有理数m,n的位置在数轴上如图所示,用不等号填空.(1)n-m______0;(2)m+n______0;(3)m-n______0;(4)n+1______0;(5)m?n______0;
(6)m+1______0.解:(1)因为n<0,m>0,所以n-m<0;
(2)因为n<0、m>0,且|n|>1、|m|<1,所以m+n<0;
(3)因为n<0,m>0,所以n-m>0;
(4)因为n<0,|n|>1,所以n+1<0;
(5)因为n<0,m>0,所以m?n<0;
(6)因为0<m<1,所以m+1>0.
做题
通过做对应的题目,来让学生更深刻理解本节知识
课堂小结
这节课我们学习了:1.不等式主要用来刻画现实生活中的不等关系2.在列不等式时,关键要确定不等号的方向,其次要确定等号能否取到3.在数轴上表示不等式时,一要选取合适的单位长度,二要确定不等式的方向,三要注意空心点与实心点之间的区别。
回忆总结
带领学生回忆本课所学
布置作业
课本P93页第1、
5、
6
题
做练习
课下练习提升
板书
3.1
认识不等式1.不等式的定义:用不等号连接的数学式子2.不等式在数轴上的表示3.应用
看黑板
帮助学生梳理本课知识点
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
8
页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
