2020-2021学年浙教版七年级数学上册第6章图形的初步知识(基础卷)(word版含解析)
文档属性
| 名称 | 2020-2021学年浙教版七年级数学上册第6章图形的初步知识(基础卷)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 233.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 08:28:09 | ||
图片预览



文档简介
第6章图形的初步知识(基础卷)
一、选择题(60分)
(2020·同步练习)下列说法正确的是
A.两点之间,直线最短
B.画出
,
两点的距离
C.连接点
与点
的线段,叫
,
两点的距离
D.两点的距离是一个数,不是指线段本身
(2020·同步练习)如图所示,某同学的家在
处,星期日他到书店去买书,想尽快赶到书店
处,请你帮助他选择一条最近的路线
A.
B.
C.
D.
(2020·同步练习)在墙壁上固定一根横放的木条,则至少需要钉子的枚数是
A.
枚
B.
枚
C.
枚
D.任意枚
(2019·期末·天津天津市和平区)如果
和
互补,且
,下列表达式:①
;②
;③
;④
中,等于
的余角的式子有
A.
个
B.
个
C.
个
D.
个
(2020·期末·北京北京市延庆区)如图,点
,,
在一条直线上,
于点
,如果
与
互余,那么图中相等的角有
A.
对
B.
对
C.
对
D.
对
(2019·单元测试·天津天津市)如图所示,某同学的家在
处,书店在
处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线
A.
B.
C.
D.
(2018·期末·广东深圳市罗湖区)木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为
A.两点之间,线段最短
B.两点确定一条直线
C.过一点,有无数条直线
D.连接两点之间的线段叫做两点间的距离
(2018·期中·云南昆明市五华区)下列叙述中,正确的是
A.相等的两个角是对顶角
B.老师测量跳远成绩的依据是两点之间,线段最短
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
(2018·期末·广东深圳市)
A.
B.
C.
D.
(2020·同步练习)若一个角为
,则它的补角的度数为
A.
B.
C.
D.
(2019·单元测试·上海上海市)如图,直线
是一条河,,
两地相距
,,
两地到
的距离分别为
,,欲在
上的某点
处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是
A.
B.
C.
D.
(2020·真题·四川凉山彝族自治州)点
是线段
的中点,点
是线段
的三等分点.若线段
,则线段
的长为
A.
B.
C.
或
D.
或
(2020·同步练习)下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是
A.③⑤⑥
B.①②③
C.③⑥
D.④⑤
(2019·单元测试)下列说法正确的是
A.棱柱的每条棱长都相等
B.棱柱侧面的形状可能是一个三角形
C.长方体的截面形状一定是长方形
D.若三棱柱的底面边长相等,则各个侧面的面积相等
(2020·专项)如图,已知
,又
,则
的度数为
A.
B.
C.
D.
二、填空题(20分)
(2020·单元测试·上海上海市)延长线段
到
,使
的长是
的
倍,则
与
的长度的比是
.
(2020·专项)如图,已知
,,
.
(2019·期末·云南昆明市官渡区)已知
平分
,若
,,则
的度数为
.
(2020·单元测试)若
,则
的补角的度数为
.
(2020·单元测试·广东广州市)一个角的余角为
,则这个角大小为
°
三、解答题(40分)
(2019·同步练习)比较下列四个时刻的时针与分针所成的角的大小,并说明理由.
,,,.
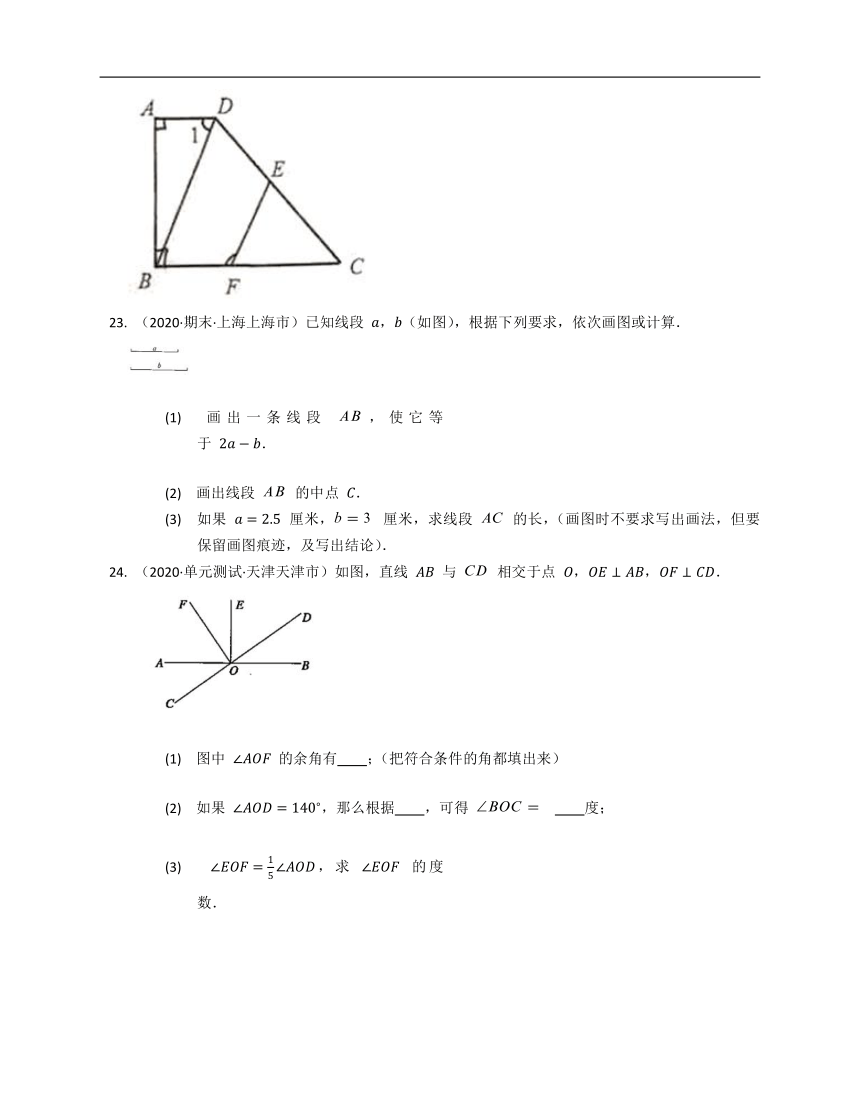
(2019·期中·上海上海市静安区)已知:如图,,,那么
吗?为什么?
(2020·期末·上海上海市)已知线段
,(如图),根据下列要求,依次画图或计算.
(1)
画出一条线段
,使它等于
.
(2)
画出线段
的中点
.
(3)
如果
厘米,
厘米,求线段
的长,(画图时不要求写出画法,但要保留画图痕迹,及写出结论).
(2020·单元测试·天津天津市)如图,直线
与
相交于点
,,.
(1)
图中
的余角有
;(把符合条件的角都填出来)
(2)
如果
,那么根据
,可得
度;
(3)
,求
的度数.
答案
一、选择题
1.
【答案】D
【知识点】直线、射线、线段的概念
表示方法
及画法、两点之间线段最短
2.
【答案】B
【知识点】线的相关概念与性质
3.
【答案】B
【知识点】两点确定一条直线
4.
【答案】C
【解析】
和
互补,
,
的余角是
,
,
,
,
即①②④,
个.
【知识点】补角的性质
5.
【答案】A
【解析】
,
,
与
互余,
,
,
,
,
,
图中相等的角有
对.
【知识点】余角的概念
6.
【答案】B
【知识点】两点之间线段最短
7.
【答案】B
【解析】在木板上画出两个点,然后过这两点弹出一条墨线,此操作的依据是两点确定一条直线.故选:B.
【知识点】两点确定一条直线
8.
【答案】C
【解析】A.相等的两个角是对顶角,错误,不合题意;
B.老师测量跳远成绩的依据是两点之间,线段最短,错误,不合题意;
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短,正确,符合题意;
D.一个角一定不等于它的余角,错误,不合题意.
【知识点】垂线段的性质、对顶角的性质、余角的性质
9.
【答案】C
【解析】
,,
.
【知识点】度分秒的换算
10.
【答案】C
【知识点】补角的概念
11.
【答案】A
【知识点】两点之间线段最短、垂线
12.
【答案】C
【解析】
是线段
的中点,,
,
点
是线段
的三等分点,
①当
时,如图,
;
②当
时,如图,
.
所以线段
的长为
或
,故选:C.
【知识点】线段的和差
13.
【答案】A
【知识点】认识立体图形
14.
【答案】D
【知识点】认识立体图形
15.
【答案】D
【解析】设
,则
,
因为
,
所以
,
所以
.
【知识点】角的计算
二、填空题
16.
【答案】
;
【知识点】线段的和差
17.
【答案】
;
【知识点】角的计算
18.
【答案】
或
;
【解析】()若射线
在
的下方时,如图
所示:
平分
,
,
又
,
,
又
,
,
;
()若射线
在
的上方时,如图
所示:
同()可得:,
又
,
.
综合所述,
的度数为
或
.
【知识点】角平分线的定义
19.
【答案】
;
【知识点】补角的性质
20.
【答案】
;
【解析】利用余角的定义可求.
【知识点】余角的概念
三、解答题
21.
【答案】
成平角;
成钝角;
成直角;
成锐角.
时最大,其次是
,再是
,最小是
时.
【知识点】钟面角
22.
【答案】
.
,
,.
.
,
.
.
【知识点】平行线及其判定、余角的性质
23.
【答案】
(1)
图略
(2)
图略
(3)
,
所以
.
【知识点】线段中点的概念及计算、线段的和差、作相等线段
24.
【答案】
(1)
,,
(2)
对顶角相等;
(3)
,,
,
,,
,
即
,
.
【知识点】对顶角、邻补角、角的计算、余角
一、选择题(60分)
(2020·同步练习)下列说法正确的是
A.两点之间,直线最短
B.画出
,
两点的距离
C.连接点
与点
的线段,叫
,
两点的距离
D.两点的距离是一个数,不是指线段本身
(2020·同步练习)如图所示,某同学的家在
处,星期日他到书店去买书,想尽快赶到书店
处,请你帮助他选择一条最近的路线
A.
B.
C.
D.
(2020·同步练习)在墙壁上固定一根横放的木条,则至少需要钉子的枚数是
A.
枚
B.
枚
C.
枚
D.任意枚
(2019·期末·天津天津市和平区)如果
和
互补,且
,下列表达式:①
;②
;③
;④
中,等于
的余角的式子有
A.
个
B.
个
C.
个
D.
个
(2020·期末·北京北京市延庆区)如图,点
,,
在一条直线上,
于点
,如果
与
互余,那么图中相等的角有
A.
对
B.
对
C.
对
D.
对
(2019·单元测试·天津天津市)如图所示,某同学的家在
处,书店在
处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线
A.
B.
C.
D.
(2018·期末·广东深圳市罗湖区)木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这是因为
A.两点之间,线段最短
B.两点确定一条直线
C.过一点,有无数条直线
D.连接两点之间的线段叫做两点间的距离
(2018·期中·云南昆明市五华区)下列叙述中,正确的是
A.相等的两个角是对顶角
B.老师测量跳远成绩的依据是两点之间,线段最短
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短
D.一个角一定不等于它的余角
(2018·期末·广东深圳市)
A.
B.
C.
D.
(2020·同步练习)若一个角为
,则它的补角的度数为
A.
B.
C.
D.
(2019·单元测试·上海上海市)如图,直线
是一条河,,
两地相距
,,
两地到
的距离分别为
,,欲在
上的某点
处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是
A.
B.
C.
D.
(2020·真题·四川凉山彝族自治州)点
是线段
的中点,点
是线段
的三等分点.若线段
,则线段
的长为
A.
B.
C.
或
D.
或
(2020·同步练习)下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是
A.③⑤⑥
B.①②③
C.③⑥
D.④⑤
(2019·单元测试)下列说法正确的是
A.棱柱的每条棱长都相等
B.棱柱侧面的形状可能是一个三角形
C.长方体的截面形状一定是长方形
D.若三棱柱的底面边长相等,则各个侧面的面积相等
(2020·专项)如图,已知
,又
,则
的度数为
A.
B.
C.
D.
二、填空题(20分)
(2020·单元测试·上海上海市)延长线段
到
,使
的长是
的
倍,则
与
的长度的比是
.
(2020·专项)如图,已知
,,
.
(2019·期末·云南昆明市官渡区)已知
平分
,若
,,则
的度数为
.
(2020·单元测试)若
,则
的补角的度数为
.
(2020·单元测试·广东广州市)一个角的余角为
,则这个角大小为
°
三、解答题(40分)
(2019·同步练习)比较下列四个时刻的时针与分针所成的角的大小,并说明理由.
,,,.
(2019·期中·上海上海市静安区)已知:如图,,,那么
吗?为什么?
(2020·期末·上海上海市)已知线段
,(如图),根据下列要求,依次画图或计算.
(1)
画出一条线段
,使它等于
.
(2)
画出线段
的中点
.
(3)
如果
厘米,
厘米,求线段
的长,(画图时不要求写出画法,但要保留画图痕迹,及写出结论).
(2020·单元测试·天津天津市)如图,直线
与
相交于点
,,.
(1)
图中
的余角有
;(把符合条件的角都填出来)
(2)
如果
,那么根据
,可得
度;
(3)
,求
的度数.
答案
一、选择题
1.
【答案】D
【知识点】直线、射线、线段的概念
表示方法
及画法、两点之间线段最短
2.
【答案】B
【知识点】线的相关概念与性质
3.
【答案】B
【知识点】两点确定一条直线
4.
【答案】C
【解析】
和
互补,
,
的余角是
,
,
,
,
即①②④,
个.
【知识点】补角的性质
5.
【答案】A
【解析】
,
,
与
互余,
,
,
,
,
,
图中相等的角有
对.
【知识点】余角的概念
6.
【答案】B
【知识点】两点之间线段最短
7.
【答案】B
【解析】在木板上画出两个点,然后过这两点弹出一条墨线,此操作的依据是两点确定一条直线.故选:B.
【知识点】两点确定一条直线
8.
【答案】C
【解析】A.相等的两个角是对顶角,错误,不合题意;
B.老师测量跳远成绩的依据是两点之间,线段最短,错误,不合题意;
C.从直线外一点到这条直线上的各点所连接的线段中,垂线段最短,正确,符合题意;
D.一个角一定不等于它的余角,错误,不合题意.
【知识点】垂线段的性质、对顶角的性质、余角的性质
9.
【答案】C
【解析】
,,
.
【知识点】度分秒的换算
10.
【答案】C
【知识点】补角的概念
11.
【答案】A
【知识点】两点之间线段最短、垂线
12.
【答案】C
【解析】
是线段
的中点,,
,
点
是线段
的三等分点,
①当
时,如图,
;
②当
时,如图,
.
所以线段
的长为
或
,故选:C.
【知识点】线段的和差
13.
【答案】A
【知识点】认识立体图形
14.
【答案】D
【知识点】认识立体图形
15.
【答案】D
【解析】设
,则
,
因为
,
所以
,
所以
.
【知识点】角的计算
二、填空题
16.
【答案】
;
【知识点】线段的和差
17.
【答案】
;
【知识点】角的计算
18.
【答案】
或
;
【解析】()若射线
在
的下方时,如图
所示:
平分
,
,
又
,
,
又
,
,
;
()若射线
在
的上方时,如图
所示:
同()可得:,
又
,
.
综合所述,
的度数为
或
.
【知识点】角平分线的定义
19.
【答案】
;
【知识点】补角的性质
20.
【答案】
;
【解析】利用余角的定义可求.
【知识点】余角的概念
三、解答题
21.
【答案】
成平角;
成钝角;
成直角;
成锐角.
时最大,其次是
,再是
,最小是
时.
【知识点】钟面角
22.
【答案】
.
,
,.
.
,
.
.
【知识点】平行线及其判定、余角的性质
23.
【答案】
(1)
图略
(2)
图略
(3)
,
所以
.
【知识点】线段中点的概念及计算、线段的和差、作相等线段
24.
【答案】
(1)
,,
(2)
对顶角相等;
(3)
,,
,
,,
,
即
,
.
【知识点】对顶角、邻补角、角的计算、余角
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
