2020-2021学年浙教版九年级数学下册第二章《直线与圆的位置关系》综合提高A卷(Word版 附答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级数学下册第二章《直线与圆的位置关系》综合提高A卷(Word版 附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 559.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 19:05:05 | ||
图片预览

文档简介
2020-2021学年浙教版九年级数学下册第二章《直线与圆的位置关系》综合提高A卷
班级_________
姓名_________
得分_________
一、选择题(每题3分,共30分)
1.三角形的内心是(
)
A.三边垂直平分线的交点
B.三条角平分线的交点
C.三条高所在直线的交点
D.三条中线的交点
2.如图所示,AB是⊙O的弦,直线BC与⊙O相切于点B,连结OA,OB,若∠ABC
=
65°,则∠A等于(
)
A.20°
B.25°
C.35°
D.75°
3.如图所示,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA
=
8,则cos∠APO等于(
)
A.
B.
C.
D.
4.在平面直角坐标系中,以点(3,
-
4)为圆心,r为半径的圆与坐标轴有且只有3个公共点,则r的值是( )
A.3
B.4
C.3或4
D.4或5
5.如图所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点.若大圆半径为2,小圆半径为1,则AB的长为(
)
A.2
B.2
C.
D.2
6.如果正三角形的内切圆半径为1,那么这个正三角形的边长为(
)
A.2
B.
C.3
D.2
7.已知△ABC的周长为14,面积为7,则△ABC的内切圆半径为(
)
A.0.5
B.1
C.2
D.3
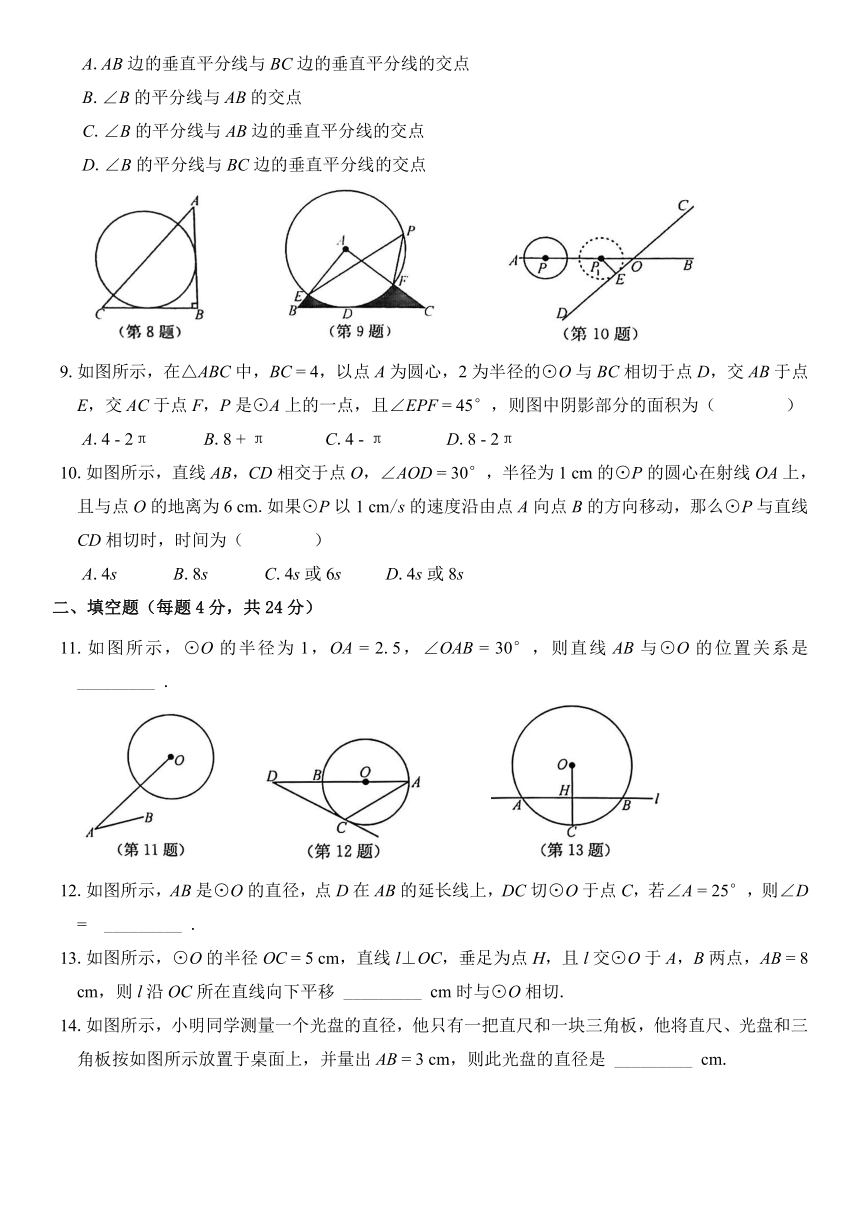
8.如图所示,在△ABC中,∠B
=
90°,AB
=
21,BC
=
20,有一个半径为10的圆分别与AB,BC相切,则此圆的圆心是(
)
A.AB边的垂直平分线与BC边的垂直平分线的交点
B.∠B的平分线与AB的交点
C.∠B的平分线与AB边的垂直平分线的交点
D.∠B的平分线与BC边的垂直平分线的交点
9.如图所示,在△ABC中,BC
=
4,以点A为圆心,2为半径的⊙O与BC相切于点D,交AB于点E,交AC于点F,P是⊙A上的一点,且∠EPF
=
45°,则图中阴影部分的面积为(
)
A.4
-
2π
B.8
+
π
C.4
-
π
D.8
-
2π
10.如图所示,直线AB,CD相交于点O,∠AOD
=
30°,半径为1
cm的⊙P的圆心在射线OA上,且与点O的地离为6
cm.如果⊙P以1
cm/s的速度沿由点A向点B的方向移动,那么⊙P与直线CD相切时,时间为(
)
A.4s
B.8s
C.4s或6s
D.4s或8s
二、填空题(每题4分,共24分)
11.如图所示,⊙O的半径为1,OA
=
2.5,∠OAB
=
30°,则直线AB与⊙O的位置关系是
_________
.
12.如图所示,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A
=
25°,则∠D
=
_________
.
13.如图所示,⊙O的半径OC
=
5
cm,直线l⊥OC,垂足为点H,且l交⊙O于A,B两点,AB
=
8
cm,则l沿OC所在直线向下平移
_________
cm时与⊙O相切.
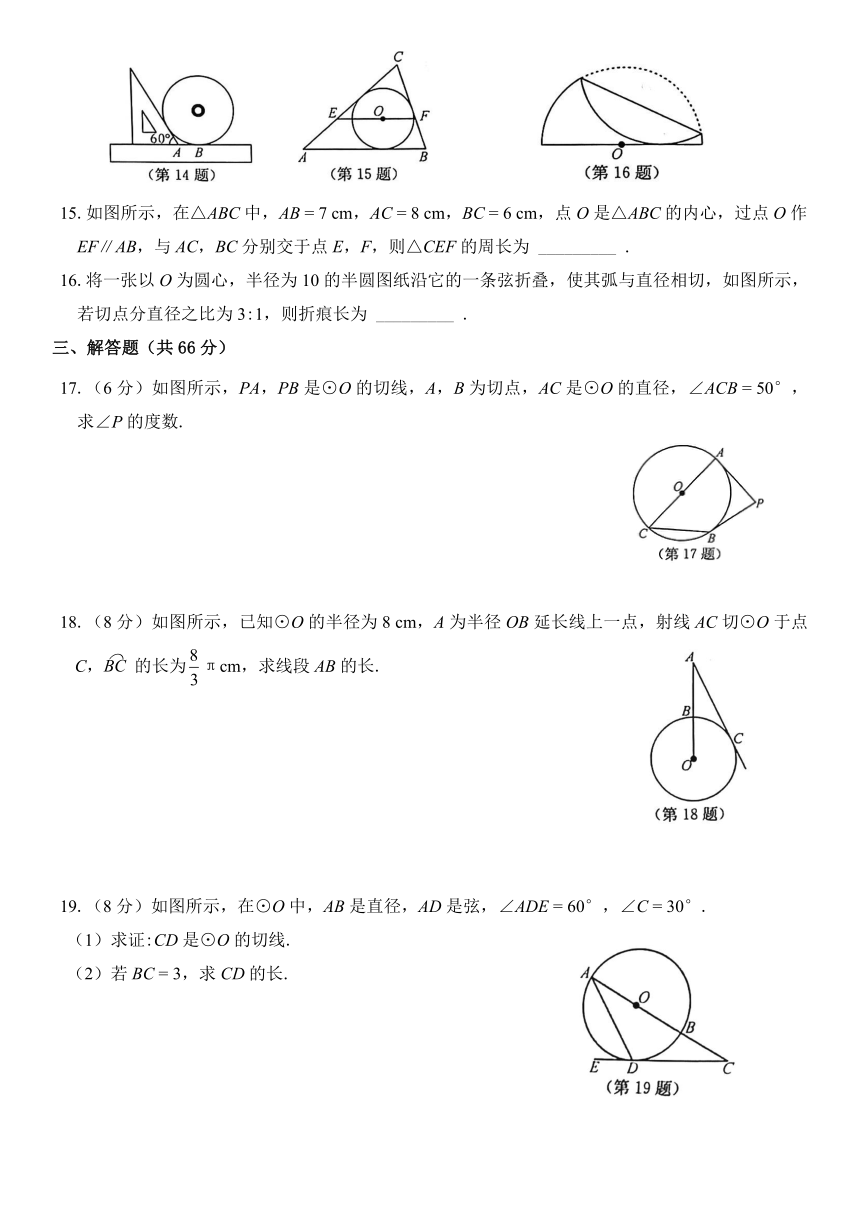
14.如图所示,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板按如图所示放置于桌面上,并量出AB
=
3
cm,则此光盘的直径是
_________
cm.
15.如图所示,在△ABC中,AB
=
7
cm,AC
=
8
cm,BC
=
6
cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则△CEF的周长为
_________
.
16.将一张以O为圆心,半径为10的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,若切点分直径之比为3:1,则折痕长为
_________
.
三、解答题(共66分)
17.(6分)如图所示,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠ACB
=
50°,求∠P的度数.
18.(8分)如图所示,已知⊙O的半径为8
cm,A为半径OB延长线上一点,射线AC切⊙O于点C,的长为πcm,求线段AB的长.
19.(8分)如图所示,在⊙O中,AB是直径,AD是弦,∠ADE
=
60°,∠C
=
30°.
(1)求证:CD是⊙O的切线.
(2)若BC
=
3,求CD的长.
20.(10分)如图所示,已知A,B,C,D,E是⊙O上五点,⊙O的直径BE
=
2,∠BCD
=
120°,A为的中点,延长BA到点P,使BA
=
AP,连结PE.
(1)求线段BD的长.
(2)求证:直线PE是⊙O的切线.
21.(10分)如图1所示,AB为⊙O的直径,C为⊙O上一点,若直线CD与⊙O相切于点C,AD⊥CD,垂足为点D.
(1)求证:△ADC∽△ACB.
(2)把直线CD向下平行移动,如图2所示,直线CD交⊙O于C,G两点,若题目中的其他条件不变,且AG
=
4,BG
=
3,求的值.
22.(12分)如图所示,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E.G是AD的中点,连结CG并延长,与BE相交于点F,延长AF与CB的延长线相交于点P,且FG
=
FB
=
3.
(1)求证:BF
=
EF.
(2)求tanP的值.
(3)求⊙O的半径.
23.(12分)如图所示,已知AB是⊙O的直径,且AB
=
12,AP是半圆的切线,C是半圆上的一动点(不与点A,B重合),过点C作CD⊥AP于点D,记∠COA
=
.
(1)当
=
60°时,求CD的长.
(2)当为何值时,CD与⊙O相切?请说明理由.
(3)当AD
=
3时,求的值.
班级_________
姓名_________
得分_________
一、选择题(每题3分,共30分)
1.三角形的内心是(
)
A.三边垂直平分线的交点
B.三条角平分线的交点
C.三条高所在直线的交点
D.三条中线的交点
2.如图所示,AB是⊙O的弦,直线BC与⊙O相切于点B,连结OA,OB,若∠ABC
=
65°,则∠A等于(
)
A.20°
B.25°
C.35°
D.75°
3.如图所示,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA
=
8,则cos∠APO等于(
)
A.
B.
C.
D.
4.在平面直角坐标系中,以点(3,
-
4)为圆心,r为半径的圆与坐标轴有且只有3个公共点,则r的值是( )
A.3
B.4
C.3或4
D.4或5
5.如图所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点.若大圆半径为2,小圆半径为1,则AB的长为(
)
A.2
B.2
C.
D.2
6.如果正三角形的内切圆半径为1,那么这个正三角形的边长为(
)
A.2
B.
C.3
D.2
7.已知△ABC的周长为14,面积为7,则△ABC的内切圆半径为(
)
A.0.5
B.1
C.2
D.3
8.如图所示,在△ABC中,∠B
=
90°,AB
=
21,BC
=
20,有一个半径为10的圆分别与AB,BC相切,则此圆的圆心是(
)
A.AB边的垂直平分线与BC边的垂直平分线的交点
B.∠B的平分线与AB的交点
C.∠B的平分线与AB边的垂直平分线的交点
D.∠B的平分线与BC边的垂直平分线的交点
9.如图所示,在△ABC中,BC
=
4,以点A为圆心,2为半径的⊙O与BC相切于点D,交AB于点E,交AC于点F,P是⊙A上的一点,且∠EPF
=
45°,则图中阴影部分的面积为(
)
A.4
-
2π
B.8
+
π
C.4
-
π
D.8
-
2π
10.如图所示,直线AB,CD相交于点O,∠AOD
=
30°,半径为1
cm的⊙P的圆心在射线OA上,且与点O的地离为6
cm.如果⊙P以1
cm/s的速度沿由点A向点B的方向移动,那么⊙P与直线CD相切时,时间为(
)
A.4s
B.8s
C.4s或6s
D.4s或8s
二、填空题(每题4分,共24分)
11.如图所示,⊙O的半径为1,OA
=
2.5,∠OAB
=
30°,则直线AB与⊙O的位置关系是
_________
.
12.如图所示,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A
=
25°,则∠D
=
_________
.
13.如图所示,⊙O的半径OC
=
5
cm,直线l⊥OC,垂足为点H,且l交⊙O于A,B两点,AB
=
8
cm,则l沿OC所在直线向下平移
_________
cm时与⊙O相切.
14.如图所示,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板按如图所示放置于桌面上,并量出AB
=
3
cm,则此光盘的直径是
_________
cm.
15.如图所示,在△ABC中,AB
=
7
cm,AC
=
8
cm,BC
=
6
cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则△CEF的周长为
_________
.
16.将一张以O为圆心,半径为10的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,若切点分直径之比为3:1,则折痕长为
_________
.
三、解答题(共66分)
17.(6分)如图所示,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠ACB
=
50°,求∠P的度数.
18.(8分)如图所示,已知⊙O的半径为8
cm,A为半径OB延长线上一点,射线AC切⊙O于点C,的长为πcm,求线段AB的长.
19.(8分)如图所示,在⊙O中,AB是直径,AD是弦,∠ADE
=
60°,∠C
=
30°.
(1)求证:CD是⊙O的切线.
(2)若BC
=
3,求CD的长.
20.(10分)如图所示,已知A,B,C,D,E是⊙O上五点,⊙O的直径BE
=
2,∠BCD
=
120°,A为的中点,延长BA到点P,使BA
=
AP,连结PE.
(1)求线段BD的长.
(2)求证:直线PE是⊙O的切线.
21.(10分)如图1所示,AB为⊙O的直径,C为⊙O上一点,若直线CD与⊙O相切于点C,AD⊥CD,垂足为点D.
(1)求证:△ADC∽△ACB.
(2)把直线CD向下平行移动,如图2所示,直线CD交⊙O于C,G两点,若题目中的其他条件不变,且AG
=
4,BG
=
3,求的值.
22.(12分)如图所示,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E.G是AD的中点,连结CG并延长,与BE相交于点F,延长AF与CB的延长线相交于点P,且FG
=
FB
=
3.
(1)求证:BF
=
EF.
(2)求tanP的值.
(3)求⊙O的半径.
23.(12分)如图所示,已知AB是⊙O的直径,且AB
=
12,AP是半圆的切线,C是半圆上的一动点(不与点A,B重合),过点C作CD⊥AP于点D,记∠COA
=
.
(1)当
=
60°时,求CD的长.
(2)当为何值时,CD与⊙O相切?请说明理由.
(3)当AD
=
3时,求的值.
