浙教版九年级数学上册第4章 相似三角形单元培优测试卷( word含解答)
文档属性
| 名称 | 浙教版九年级数学上册第4章 相似三角形单元培优测试卷( word含解答) |

|
|
| 格式 | zip | ||
| 文件大小 | 373.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-23 00:00:00 | ||
图片预览


文档简介
2020年秋浙教版九年级数学上册第4章
相似三角形单元培优测试卷
一、选择题(共10题;共30分)
1.已知
,那么下列等式中,不一定正确的是(???
)
A.???????B.????????????????C.???????????????D.?
2.如图,直线a∥b∥c
,
分别交直线m
,
n于点A
,
B
,
C
,
D
,
E
,
F
,
若AB=2,BC=4,DE=3,则EF的长是(???
)
A.?5?????????????????????B.?6?????????????????????????C.?7?????????????????????????????D.?8
3.如图,三角形ABC中,D,E分别为边AB,AC上的一点,且DE平行于BC,S△ADE=S四边形DECB
,
则△ABC与△ADE相似比的值为(??
)
A.?2???????????????B.?4??????????????????????C.?????????????????????D.?
4.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为(??
)
A.?2.2???????????????????B.?2.5????????????????????????C.?2????????????????????????????D.?1.8
5.如图,等腰
与等腰
是以点O为位似中心的位似图形,位似比为
,则点D的坐标是(?
)
A.???????????????B.????????????????C.??????????????????D.?
6.宽与长的比是
(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形
,分别取
的中点
,连接
,以点F为圆心,以
为半径画弧,交
的延长线于点G;作
,交
的延长线于点H,则图中下列矩形是黄金矩形的是(??
)
A.?矩形ABEF?????????B.?矩形EFCD????????????C.?矩形EFGH?????????????D.?矩形ABGH
7.如图,在正三角形
中,分别在
,
上,且
,
,则有(???
)
A.?????B.???????C.????????D.?
8.如图,AB是
O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若BF=FE=2,FC=1,则AC的长是(??
)
A.??????????????????B.?????????????????C.?????????????????????D.?
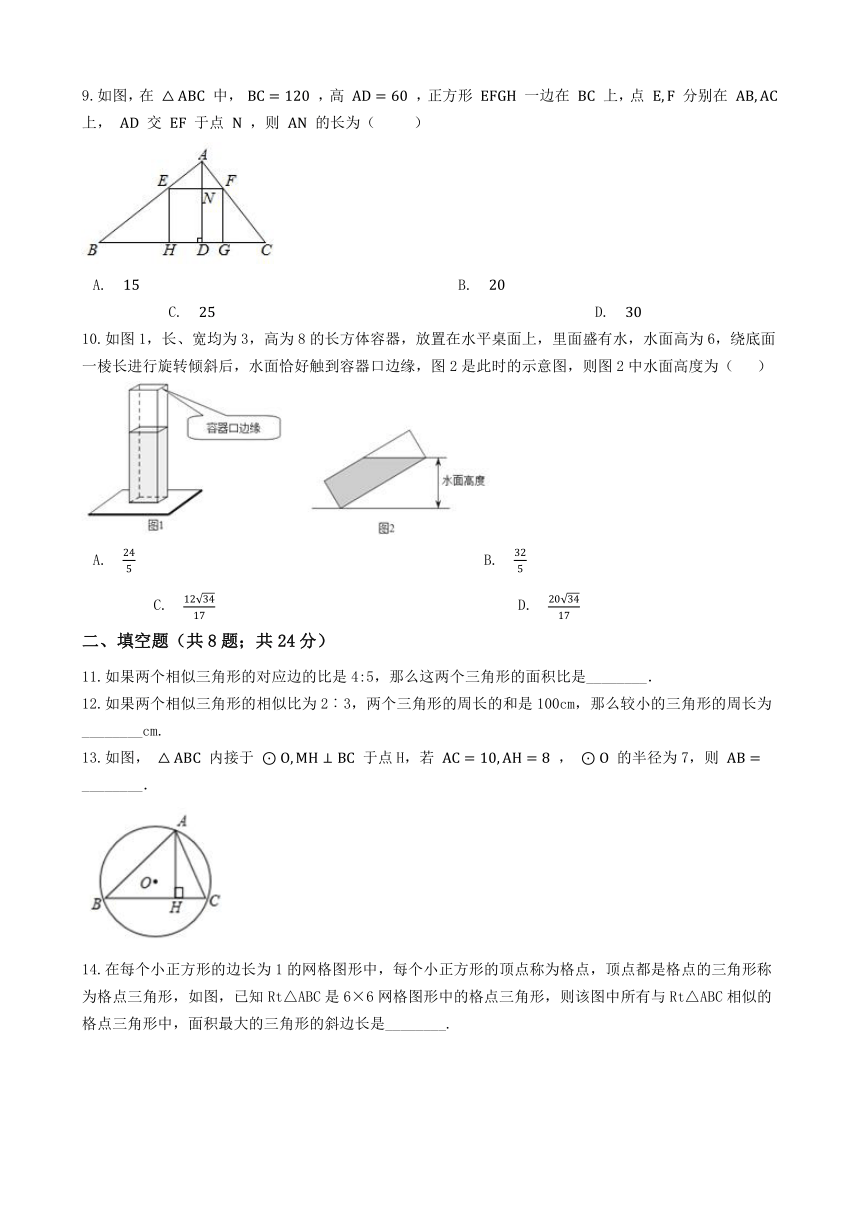
9.如图,在
中,
,高
,正方形
一边在
上,点
分别在
上,
交
于点
,则
的长为(??
)
A.??????????????????????B.???????????????????????C.??????????????????????????D.?
10.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为(?
)
A.????????????????????????B.?????????????????????C.?????????????????????D.?
二、填空题(共8题;共24分)
11.如果两个相似三角形的对应边的比是4:5,那么这两个三角形的面积比是________.
12.如果两个相似三角形的相似比为2︰3,两个三角形的周长的和是100cm,那么较小的三角形的周长为________cm.
13.如图,
内接于
于点H,若
,
的半径为7,则
________.
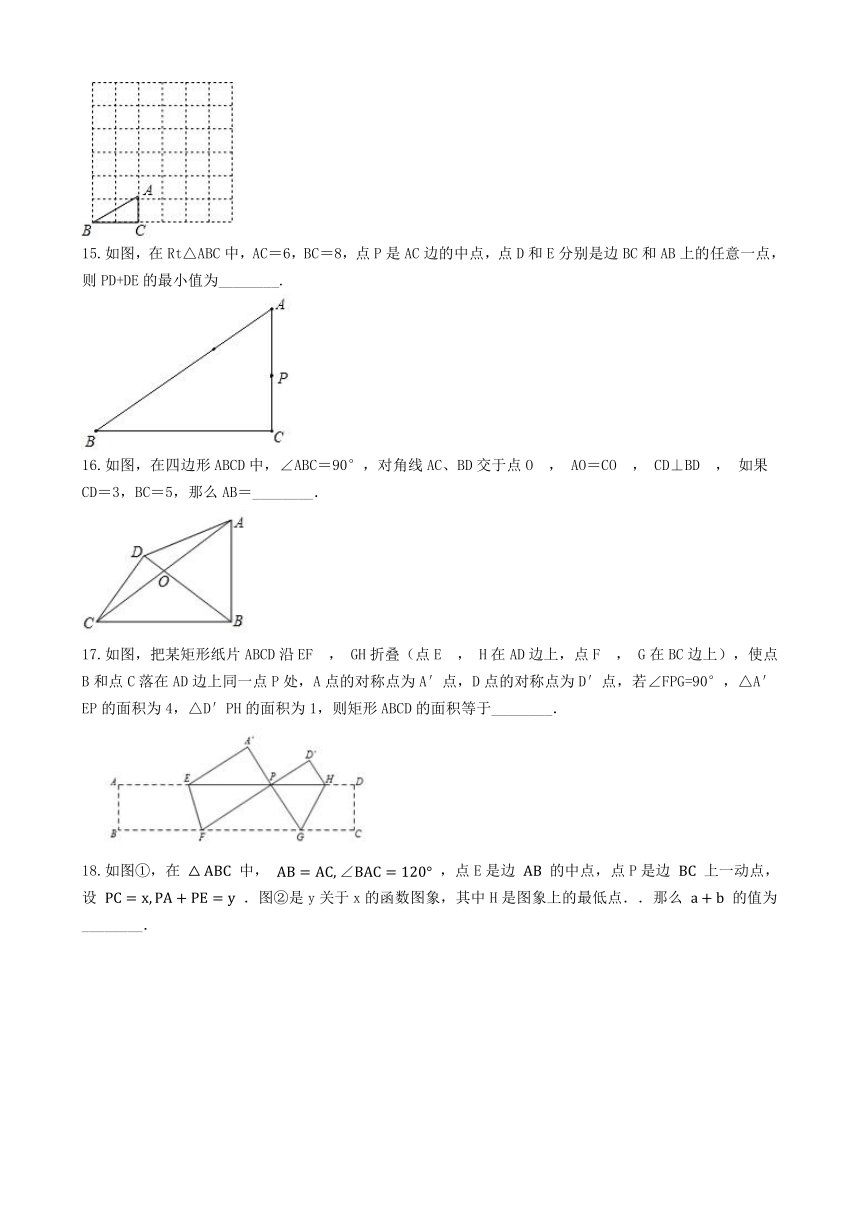
14.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是________.
15.如图,在Rt△ABC中,AC=6,BC=8,点P是AC边的中点,点D和E分别是边BC和AB上的任意一点,则PD+DE的最小值为________.
16.如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O
,
AO=CO
,
CD⊥BD
,
如果CD=3,BC=5,那么AB=________.
17.如图,把某矩形纸片ABCD沿EF
,
GH折叠(点E
,
H在AD边上,点F
,
G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A′点,D点的对称点为D′点,若∠FPG=90°,△A′EP的面积为4,△D′PH的面积为1,则矩形ABCD的面积等于________.
?
???
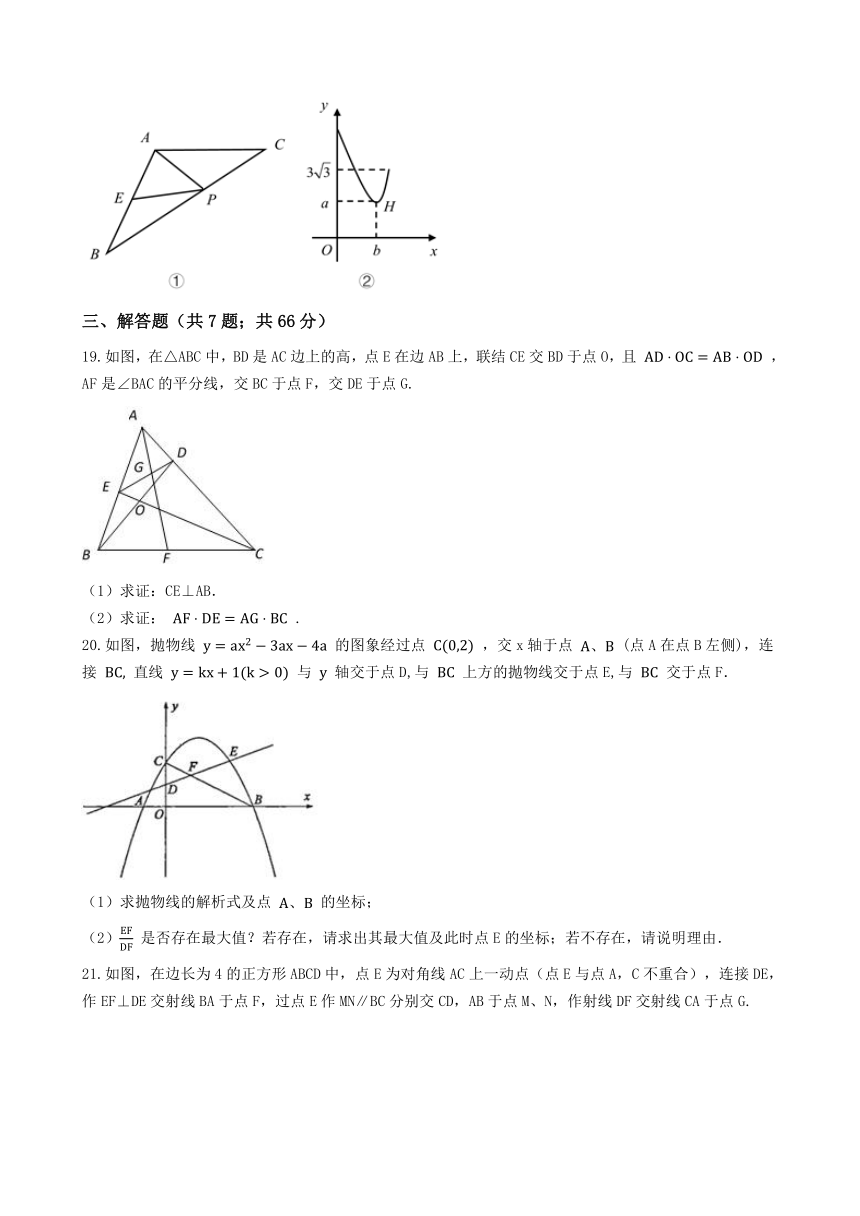
18.如图①,在
中,
,点E是边
的中点,点P是边
上一动点,设
.图②是y关于x的函数图象,其中H是图象上的最低点..那么
的值为________.
三、解答题(共7题;共66分)
19.如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且
,AF是∠BAC的平分线,交BC于点F,交DE于点G.
(1)求证:CE⊥AB.
(2)求证:
.
20.如图,抛物线
的图象经过点
,交x轴于点
(点A在点B左侧),连接
直线
与
轴交于点D,与
上方的抛物线交于点E,与
交于点F.
(1)求抛物线的解析式及点
的坐标;
(2)
是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
21.如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.
22.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD
,
∠ADE=30°,连接CE
.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x
,
当CD=2CE时,求x的值.
23.如图1,在矩形ABCO中,OA=8,OC=6,D
,
E分别是AB
,
BC上一点,AD=2,CE=3,OE与CD相交于点F
.
(1)求证:OE⊥CD;
(2)如图2,点G是CD的中点,延长OG交BC于H
,
求CH的长.
24.如图,在
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
是一个格点三角形.
(1)在图
中,请判断
与
是否相似,并说明理由;
(2)在图
中,以O为位似中心,再画一个格点三角形,使它与
的位似比为2:1
(3)在图
中,请画出所有满足条件的格点三角形,它与
相似,且有一条公共边和一个公共角.
25.在平面直角坐标系
中,把与x轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线
的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线
与
是“共根抛物线”,其顶点为P.
???
(1)若抛物线
经过点
,求
对应的函数表达式;
(2)当
的值最大时,求点P的坐标;
(3)设点Q是抛物线
上的一个动点,且位于其对称轴的右侧.若
与
相似,求其“共根抛物线”
的顶点P的坐标.
答案
一、选择题
1.A、由比例的性质得到3y=5x,故本选项不符合题意.
B、根据比例的性质得到x+y=8k(k是正整数),故本选项符合题意.
C、根据合比性质得到
,故本选项不符合题意.
D、根据等比性质得到
,故本选项不符合题意.
故答案为:B.
2.∵直线a∥b∥c
,
∴
,即
,
∴EF=6.
故答案为:B
.
3.解:∵S△ADE=S四边形DECB
,
∴S△ABC=2S△ADE
,
∵DE∥BC,
∴△ADE∽△ABC,
∴
,
即
,
即△ABC与△ADE相似比的值是
,
故答案为:C.
4.解:如图1,连接BD、CD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=
=
=
,
∵弦AD平分∠BAC,
∴CD=BD=
,
∴∠CBD=∠DAB,
在△ABD和△BED中,
∴△ABD∽△BED,
∴
=
,即
,
解得DE=
.
故答案为:A.
5.解:∵等腰
与等腰
是以点O为位似中心的位似图形,位似比为
,
∴
,即:DE=3BC=12,
∴CE=DE=12,
∴
,解得:OC=6,
∴OE=6+12=18,
∴点
的坐标是:
.
故答案为:A.
6.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF=
∴FG=
∴CG=
?1
∴
∴矩形DCGH为黄金矩形
故答案为:D.
7.由已知中正三角形ABC中,D、E分别在AC、AB上,
,AE=BE,
易判断出:△AED为一个锐角三角形,△BED为一个钝角三角形,故A不符合题意;
△ABD也是一个钝角三角形,故C也不符合题意;
但△BCD为一个锐角三角形,故D也不符合题意;
故答案为:B.
8.解:连接BC,
∵AB是
O的直径,
∴∠ACB=90°,
∴∠ACE+∠BCF=90°,
∵BF⊥CD,
∴∠CFB=90°,
∴∠CBF+∠BC=90°,
∴∠ACE=∠CBF,
∵AE⊥CD,
∴∠AEC=∠CFB=90°,
,
∴
,
∵FB=FE=2,FC=1,
∴CE=CF+EF=3,
,
∴
,
∴
,
故答案为:B.
9.解:∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴
.
设AN=x,则EF=FG=DN=60-x,
∴
解得:x=20
所以,AN=20.
故答案为:B.
10.解:过点C作CF⊥BG于F,如图所示:
设DE=x,则AD=8-x,
根据题意得:
(8-x+8)×3×3=3×3×6,
解得:x=4,
∴DE=4,
∵∠E=90°,
由勾股定理得:CD=
,
∵∠BCE=∠DCF=90°,
∴∠DCE=∠BCF,
∵∠DEC=∠BFC=90°,
∴△CDE∽△BCF,
∴
,
即
,
∴CF=
.
故答案为:A.
二、填空题
11.解:∵两个相似三角形的相似比为:
,
∴这两个三角形的面积比
;
故答案为:16∶25.
12.设两个三角形的周长分别为
由已知,得
解得
∴较小的三角形的周长为40
cm.
13.解:作直径AD,连接BD,
∵AD为直径,
∴∠ABD=90°,又AH⊥BC,
∴∠ABD=∠AHC,
由圆周角定理得,∠D=∠C,
∴△ABD∽△AHC,
∴
,即
,
解得,AB=
,
故答案为:
.
14.解:
在
中,
,
,
,
,
与
相似的格点三角形的两直角边的比值为
,
若该三角形最短边长为4,则另一直角边长为8,但在
网格图形中,最长线段为
,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出
,
,
的三角形,
,
,
,
此时
的面积为:
,
为面积最大的三角形,其斜边长为:
.
故答案为:
.
15.解:作点P关于BC的对称点F,过F作FE⊥AB于E交BC于D,
则此时,PD+DE的值最小,且PD+DE的最小值=EF,
∴CF=CP,
∵点P是AC边的中点,
∴AP=PC=3,
∴AF=9,
∵在Rt△ABC中,AC=6,BC=8,
∴AB=10,
∵∠AEF=∠ACB=90°,
∴∠A+∠B=∠A+∠F,
∴∠B=∠F,
∴△ABC∽△AFE,
∴
=
,
∴
=
,
∴EF=
,
∴PD+DE的最小值为
,
答案为:
.
16.过点A作AE⊥BD
,
∵CD⊥BD
,
AE⊥BD
,
∴∠CDB=∠AED=90°,CO=AO
,
∠COD=∠AOE
,
∴△AOE≌△COD(AAS)
∴CD=AE=3,
∵∠CDB=90°,BC=5,CD=3,
∴DB=
=4,
∵∠ABC=∠AEB=90°,
∴∠ABE+∠EAB=90°,∠CBD+∠ABE=90°,
∴∠EAB=∠CBD
,
又∵∠CDB=∠AEB=90°,
∴△ABE∽△BCD
,
∴
,
∴
,
∴AB=
.
故答案为:
.
17.解:∵四边形ABCD是矩形,
∴AB=CD,
由折叠可知
:PA'=AB,PD'=CD,
∴PD'=PA',
∵∠FPG=90?,∠EPF=∠D'PH,∠GPH=∠A'PE,
∴∠A'PE+∠D'PH=∠EPF+∠GPH=90?,
∵∠A'EP+A'PE=90?,
∴∠A'EP=∠D'PH,
∴?A'EP∽?D'PH,
∵△A′EP的面积为4,△D′PH的面积为1,
∴
,
设D'H=k,则A'P=PD'=2k,A'E=4k,
∵S?D'PH=PD'·D'H=·k·2k=1,
∴k=1,
∴PH=
,
PE=
,
∴AD=AE+EP+PH+HP=4+2++1=5+3
,
∵AB=2k=2,
∴S矩形ABCD=AB·AD=2(5+3)=10+6.
故答案为:10+6.
18.解:如图,过B作AC的平行线,过C作AB的平行线,交于点D,
可得四边形ABCD为平行四边形,又AB=AC,
∴四边形ABCD为菱形,点A和点D关于BC对称,
∴PA+PE=PD+PE,
当P,D,E共线时,PA+PE最小,即DE的长,
观察图像可知:当点P与点B重合时,PD+PE=
,
∵点E是AB中点,
∴BE+BD=3BE=
,
∴BE=
,AB=BD=
,
∵∠BAC=120°,
∴∠ABD=(180°-120°)÷2×2=60°,
∴△ABD为等边三角形,
∴DE⊥AB,∠BDE=30°,
∴DE=3,即PA+PE的最小值为3,
即点H的纵坐标为a=3,
当点P为DE和BC交点时,
∵AB∥CD,
∴△PBE∽△PCD,
∴
,
∵菱形ABCD中,AD⊥BC,
∴BC=2×
=6,
∴
,
解得:PC=4,
即点H的横坐标为b=4,
∴a+b=3+4=7,
故答案为:7.
三、解答题
19.(1)证明:∵
,
∴
.
∵BD是AC边上的高,
∴∠BDC
=
90°,△ADB和△ODC是直角三角形.
∴Rt△ADB∽Rt△ODC.
∴∠ABD
=∠OCD.
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,
∠EOB
+∠ABD+∠OEB
=180°.
∴∠OEB
=
90°.
∴CE⊥AB.
(2)证明:在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD
=∠OCD,
∴△ADB∽△AEC.
∴
,
即
.
在△DAE和△BAC中
∵∠DAE
=∠BAC,
.
∴△DAE∽△BAC.
∵AF是∠BAC的平分线,
∴
,即
.
20.
(1)解:把
代入
,即
,解得
∴抛物线的解析式为
令
可得:
∴
;
(2)解:存在,
如图,由题意,点E在y轴的右侧,作
轴,交
于点G
直线
与
轴交于点
∴
,
设
所在直线的解析式为
,
将
代入上述解析式得:
解得:
的解析式为
设
则
,其中
.
∴抛物线开口方向朝下
∴当
时,有最大值,最大值为
.
将t=2代入
=-2+3+2=3
∴点
的坐标为
.
21.
(1)证明:∵四边形ABCD是正方形,AC是对角线,
∴∠ECM=45°,
∵MN∥BC,∠BCM=90°,
∴∠NMC+∠BCM=180°,∠MNB+∠B=180°,
∴∠NMC=90°,∠MNB=90°,
∴∠MEC=∠MCE=45°,∠DME=∠ENF=90°,
∴MC=ME,
∵CD=MN,
∴DM=EN,
∵DE⊥EF,∠EDM+∠DEM=90°,
∴∠DEF=90°,
∴∠DEM+∠FEN=90°,
∴∠EDM=∠FEN,
在△DME和△ENF中,
,
∴△DME≌△ENF(ASA),
∴EF=DE;
(2)解:由(1)知,△DME≌△ENF,
∴ME=NF,
∵四边形MNBC是矩形,
∴MC=BN,
又∵ME=MC,AB=4,AF=2,
∴BN=MC=NF=1,
∵∠EMC=90°,
∴CE=
,
∵AF∥CD,
∴△DGC∽△FGA,
∴
,
∴
,
∵AB=BC=4,∠B=90°,
∴AC=4
,
∵AC=AG+GC,
∴AG=
,CG=
,
∴GE=GC﹣CE=
=
.
22.
(1)∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴
,
∴
,
∵∠EAC=∠DAB,
∴△ACE∽△ABD;
(3)在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB=
=4
,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴
,
∴
,
∴BD=
x,
∴BC=CD+BD=2x+
x=8,
解得:x=16﹣8
.
23.(1)∵四边形ABCO是矩形,
∴OA=BC=8,OC=AB=6,
在Rt△OCE中,CE=3,
∴OE=
,
∵AB∥OC,即AD∥OC,且AD=2,
∴
,
∴
,
∴PA=4,
∴PO=PA+OA=12,
∴在Rt△OPC中,OC=6,
∴CP=
,
∵OA∥BC,即OP∥CE,
∴
,
∴
,
∴EF=
OE=
,
CF=
CP=
,
∵(
)2+(
)2=
=9,
∴EF2+CF2=CE2
,
∴△CEF是直角三角形,
∴∠CFE=90°,
∴OE⊥CD;
(2)在Rt△CBD中,CB=8,BD=AB﹣AD=6﹣2=4,
根据勾股定理,得CD=
,
∵点G是CD的中点,
∴CG=DG=2
,
由(1)知:CP=6
,
∴DP=CP﹣CD=2
,
∴点G是CP的三等分点,
∵OA∥BC,即OP∥CH,
∴
,
∴
,
∴CH=6.
答:CH的长为6.
24.
(1)解:如图
所示:
与
相似,
理由:
;
,
,
与
相似;
(2)解:如图
所示:
即为所求;
(3)解:如图
所示:
和
即为所求.??
25.
(1)解:当
时,
,解得
,
.
∴
、
、
.
由题意得,设
对应的函数表达式为
,
又∵
经过点
,
∴
,
∴
.
∴
对应的函数表达式为
.
(2)解:∵
、
与
轴交点均为
、
,
∴
、
的对称轴都是直线
.
∴点
在直线
上.
∴
.
如图1,当A、C、P三点共线时,
的值最大,
此时点P为直线
与直线
的交点.
由
、
可求得,直线
对应的函数表达式为
.
∴点
.
(3)解:
由题意可得,
,
,
,
因为在
中,
,故
.
由
,得顶点
.
因为
的顶点P在直线
上,点Q在
上,
∴
不可能是直角.
第一种情况:当
时,
①如图2,当
时,则得
.
设
,则
,
∴
.
由
得
,解得
.
∵
时,点Q与点P重合,不符合题意,
∴舍去,此时
.
②如图3,当
时,则得
.
设
,则
.
∴
.
由
得
,解得
(舍),此时
.
第二种情况:当
时,
①如图4,当
时,则得
.
过Q作
交对称轴于点M,∴
.
∴
.由图2可知
,
∴
.
∴
,又
,代入得
.
∵点
,
∴点
.
②如图5,当
时,则
.
过Q作
交对称轴于点M,
∴
,则
.
由图3可知
,
,
∴
,
,
∴
.
又
,代入得
.
∵点
,
∴点
,
综上所述,
或
或
或
.
相似三角形单元培优测试卷
一、选择题(共10题;共30分)
1.已知
,那么下列等式中,不一定正确的是(???
)
A.???????B.????????????????C.???????????????D.?
2.如图,直线a∥b∥c
,
分别交直线m
,
n于点A
,
B
,
C
,
D
,
E
,
F
,
若AB=2,BC=4,DE=3,则EF的长是(???
)
A.?5?????????????????????B.?6?????????????????????????C.?7?????????????????????????????D.?8
3.如图,三角形ABC中,D,E分别为边AB,AC上的一点,且DE平行于BC,S△ADE=S四边形DECB
,
则△ABC与△ADE相似比的值为(??
)
A.?2???????????????B.?4??????????????????????C.?????????????????????D.?
4.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为(??
)
A.?2.2???????????????????B.?2.5????????????????????????C.?2????????????????????????????D.?1.8
5.如图,等腰
与等腰
是以点O为位似中心的位似图形,位似比为
,则点D的坐标是(?
)
A.???????????????B.????????????????C.??????????????????D.?
6.宽与长的比是
(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形:作正方形
,分别取
的中点
,连接
,以点F为圆心,以
为半径画弧,交
的延长线于点G;作
,交
的延长线于点H,则图中下列矩形是黄金矩形的是(??
)
A.?矩形ABEF?????????B.?矩形EFCD????????????C.?矩形EFGH?????????????D.?矩形ABGH
7.如图,在正三角形
中,分别在
,
上,且
,
,则有(???
)
A.?????B.???????C.????????D.?
8.如图,AB是
O的直径,CD是弦,AE⊥CD于点E,BF⊥CD于点F.若BF=FE=2,FC=1,则AC的长是(??
)
A.??????????????????B.?????????????????C.?????????????????????D.?
9.如图,在
中,
,高
,正方形
一边在
上,点
分别在
上,
交
于点
,则
的长为(??
)
A.??????????????????????B.???????????????????????C.??????????????????????????D.?
10.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为(?
)
A.????????????????????????B.?????????????????????C.?????????????????????D.?
二、填空题(共8题;共24分)
11.如果两个相似三角形的对应边的比是4:5,那么这两个三角形的面积比是________.
12.如果两个相似三角形的相似比为2︰3,两个三角形的周长的和是100cm,那么较小的三角形的周长为________cm.
13.如图,
内接于
于点H,若
,
的半径为7,则
________.
14.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形,如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中,面积最大的三角形的斜边长是________.
15.如图,在Rt△ABC中,AC=6,BC=8,点P是AC边的中点,点D和E分别是边BC和AB上的任意一点,则PD+DE的最小值为________.
16.如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O
,
AO=CO
,
CD⊥BD
,
如果CD=3,BC=5,那么AB=________.
17.如图,把某矩形纸片ABCD沿EF
,
GH折叠(点E
,
H在AD边上,点F
,
G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A′点,D点的对称点为D′点,若∠FPG=90°,△A′EP的面积为4,△D′PH的面积为1,则矩形ABCD的面积等于________.
?
???
18.如图①,在
中,
,点E是边
的中点,点P是边
上一动点,设
.图②是y关于x的函数图象,其中H是图象上的最低点..那么
的值为________.
三、解答题(共7题;共66分)
19.如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且
,AF是∠BAC的平分线,交BC于点F,交DE于点G.
(1)求证:CE⊥AB.
(2)求证:
.
20.如图,抛物线
的图象经过点
,交x轴于点
(点A在点B左侧),连接
直线
与
轴交于点D,与
上方的抛物线交于点E,与
交于点F.
(1)求抛物线的解析式及点
的坐标;
(2)
是否存在最大值?若存在,请求出其最大值及此时点E的坐标;若不存在,请说明理由.
21.如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.
22.如图,在Rt△ABC中,AC=4,∠BAC=90°,∠B=30°,D是BC上一点,AE⊥AD
,
∠ADE=30°,连接CE
.
(1)求证:△ADE∽△ABC;
(2)求证:△ACE∽△ABD;
(3)设CE=x
,
当CD=2CE时,求x的值.
23.如图1,在矩形ABCO中,OA=8,OC=6,D
,
E分别是AB
,
BC上一点,AD=2,CE=3,OE与CD相交于点F
.
(1)求证:OE⊥CD;
(2)如图2,点G是CD的中点,延长OG交BC于H
,
求CH的长.
24.如图,在
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
是一个格点三角形.
(1)在图
中,请判断
与
是否相似,并说明理由;
(2)在图
中,以O为位似中心,再画一个格点三角形,使它与
的位似比为2:1
(3)在图
中,请画出所有满足条件的格点三角形,它与
相似,且有一条公共边和一个公共角.
25.在平面直角坐标系
中,把与x轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线
的顶点为D,交x轴于点A、B(点A在点B左侧),交y轴于点C.抛物线
与
是“共根抛物线”,其顶点为P.
???
(1)若抛物线
经过点
,求
对应的函数表达式;
(2)当
的值最大时,求点P的坐标;
(3)设点Q是抛物线
上的一个动点,且位于其对称轴的右侧.若
与
相似,求其“共根抛物线”
的顶点P的坐标.
答案
一、选择题
1.A、由比例的性质得到3y=5x,故本选项不符合题意.
B、根据比例的性质得到x+y=8k(k是正整数),故本选项符合题意.
C、根据合比性质得到
,故本选项不符合题意.
D、根据等比性质得到
,故本选项不符合题意.
故答案为:B.
2.∵直线a∥b∥c
,
∴
,即
,
∴EF=6.
故答案为:B
.
3.解:∵S△ADE=S四边形DECB
,
∴S△ABC=2S△ADE
,
∵DE∥BC,
∴△ADE∽△ABC,
∴
,
即
,
即△ABC与△ADE相似比的值是
,
故答案为:C.
4.解:如图1,连接BD、CD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=
=
=
,
∵弦AD平分∠BAC,
∴CD=BD=
,
∴∠CBD=∠DAB,
在△ABD和△BED中,
∴△ABD∽△BED,
∴
=
,即
,
解得DE=
.
故答案为:A.
5.解:∵等腰
与等腰
是以点O为位似中心的位似图形,位似比为
,
∴
,即:DE=3BC=12,
∴CE=DE=12,
∴
,解得:OC=6,
∴OE=6+12=18,
∴点
的坐标是:
.
故答案为:A.
6.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF=
∴FG=
∴CG=
?1
∴
∴矩形DCGH为黄金矩形
故答案为:D.
7.由已知中正三角形ABC中,D、E分别在AC、AB上,
,AE=BE,
易判断出:△AED为一个锐角三角形,△BED为一个钝角三角形,故A不符合题意;
△ABD也是一个钝角三角形,故C也不符合题意;
但△BCD为一个锐角三角形,故D也不符合题意;
故答案为:B.
8.解:连接BC,
∵AB是
O的直径,
∴∠ACB=90°,
∴∠ACE+∠BCF=90°,
∵BF⊥CD,
∴∠CFB=90°,
∴∠CBF+∠BC=90°,
∴∠ACE=∠CBF,
∵AE⊥CD,
∴∠AEC=∠CFB=90°,
,
∴
,
∵FB=FE=2,FC=1,
∴CE=CF+EF=3,
,
∴
,
∴
,
故答案为:B.
9.解:∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴
.
设AN=x,则EF=FG=DN=60-x,
∴
解得:x=20
所以,AN=20.
故答案为:B.
10.解:过点C作CF⊥BG于F,如图所示:
设DE=x,则AD=8-x,
根据题意得:
(8-x+8)×3×3=3×3×6,
解得:x=4,
∴DE=4,
∵∠E=90°,
由勾股定理得:CD=
,
∵∠BCE=∠DCF=90°,
∴∠DCE=∠BCF,
∵∠DEC=∠BFC=90°,
∴△CDE∽△BCF,
∴
,
即
,
∴CF=
.
故答案为:A.
二、填空题
11.解:∵两个相似三角形的相似比为:
,
∴这两个三角形的面积比
;
故答案为:16∶25.
12.设两个三角形的周长分别为
由已知,得
解得
∴较小的三角形的周长为40
cm.
13.解:作直径AD,连接BD,
∵AD为直径,
∴∠ABD=90°,又AH⊥BC,
∴∠ABD=∠AHC,
由圆周角定理得,∠D=∠C,
∴△ABD∽△AHC,
∴
,即
,
解得,AB=
,
故答案为:
.
14.解:
在
中,
,
,
,
,
与
相似的格点三角形的两直角边的比值为
,
若该三角形最短边长为4,则另一直角边长为8,但在
网格图形中,最长线段为
,但此时画出的直角三角形为等腰直角三角形,从而画不出端点都在格点且长为8的线段,故最短直角边长应小于4,在图中尝试,可画出
,
,
的三角形,
,
,
,
此时
的面积为:
,
为面积最大的三角形,其斜边长为:
.
故答案为:
.
15.解:作点P关于BC的对称点F,过F作FE⊥AB于E交BC于D,
则此时,PD+DE的值最小,且PD+DE的最小值=EF,
∴CF=CP,
∵点P是AC边的中点,
∴AP=PC=3,
∴AF=9,
∵在Rt△ABC中,AC=6,BC=8,
∴AB=10,
∵∠AEF=∠ACB=90°,
∴∠A+∠B=∠A+∠F,
∴∠B=∠F,
∴△ABC∽△AFE,
∴
=
,
∴
=
,
∴EF=
,
∴PD+DE的最小值为
,
答案为:
.
16.过点A作AE⊥BD
,
∵CD⊥BD
,
AE⊥BD
,
∴∠CDB=∠AED=90°,CO=AO
,
∠COD=∠AOE
,
∴△AOE≌△COD(AAS)
∴CD=AE=3,
∵∠CDB=90°,BC=5,CD=3,
∴DB=
=4,
∵∠ABC=∠AEB=90°,
∴∠ABE+∠EAB=90°,∠CBD+∠ABE=90°,
∴∠EAB=∠CBD
,
又∵∠CDB=∠AEB=90°,
∴△ABE∽△BCD
,
∴
,
∴
,
∴AB=
.
故答案为:
.
17.解:∵四边形ABCD是矩形,
∴AB=CD,
由折叠可知
:PA'=AB,PD'=CD,
∴PD'=PA',
∵∠FPG=90?,∠EPF=∠D'PH,∠GPH=∠A'PE,
∴∠A'PE+∠D'PH=∠EPF+∠GPH=90?,
∵∠A'EP+A'PE=90?,
∴∠A'EP=∠D'PH,
∴?A'EP∽?D'PH,
∵△A′EP的面积为4,△D′PH的面积为1,
∴
,
设D'H=k,则A'P=PD'=2k,A'E=4k,
∵S?D'PH=PD'·D'H=·k·2k=1,
∴k=1,
∴PH=
,
PE=
,
∴AD=AE+EP+PH+HP=4+2++1=5+3
,
∵AB=2k=2,
∴S矩形ABCD=AB·AD=2(5+3)=10+6.
故答案为:10+6.
18.解:如图,过B作AC的平行线,过C作AB的平行线,交于点D,
可得四边形ABCD为平行四边形,又AB=AC,
∴四边形ABCD为菱形,点A和点D关于BC对称,
∴PA+PE=PD+PE,
当P,D,E共线时,PA+PE最小,即DE的长,
观察图像可知:当点P与点B重合时,PD+PE=
,
∵点E是AB中点,
∴BE+BD=3BE=
,
∴BE=
,AB=BD=
,
∵∠BAC=120°,
∴∠ABD=(180°-120°)÷2×2=60°,
∴△ABD为等边三角形,
∴DE⊥AB,∠BDE=30°,
∴DE=3,即PA+PE的最小值为3,
即点H的纵坐标为a=3,
当点P为DE和BC交点时,
∵AB∥CD,
∴△PBE∽△PCD,
∴
,
∵菱形ABCD中,AD⊥BC,
∴BC=2×
=6,
∴
,
解得:PC=4,
即点H的横坐标为b=4,
∴a+b=3+4=7,
故答案为:7.
三、解答题
19.(1)证明:∵
,
∴
.
∵BD是AC边上的高,
∴∠BDC
=
90°,△ADB和△ODC是直角三角形.
∴Rt△ADB∽Rt△ODC.
∴∠ABD
=∠OCD.
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,
∠EOB
+∠ABD+∠OEB
=180°.
∴∠OEB
=
90°.
∴CE⊥AB.
(2)证明:在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD
=∠OCD,
∴△ADB∽△AEC.
∴
,
即
.
在△DAE和△BAC中
∵∠DAE
=∠BAC,
.
∴△DAE∽△BAC.
∵AF是∠BAC的平分线,
∴
,即
.
20.
(1)解:把
代入
,即
,解得
∴抛物线的解析式为
令
可得:
∴
;
(2)解:存在,
如图,由题意,点E在y轴的右侧,作
轴,交
于点G
直线
与
轴交于点
∴
,
设
所在直线的解析式为
,
将
代入上述解析式得:
解得:
的解析式为
设
则
,其中
.
∴抛物线开口方向朝下
∴当
时,有最大值,最大值为
.
将t=2代入
=-2+3+2=3
∴点
的坐标为
.
21.
(1)证明:∵四边形ABCD是正方形,AC是对角线,
∴∠ECM=45°,
∵MN∥BC,∠BCM=90°,
∴∠NMC+∠BCM=180°,∠MNB+∠B=180°,
∴∠NMC=90°,∠MNB=90°,
∴∠MEC=∠MCE=45°,∠DME=∠ENF=90°,
∴MC=ME,
∵CD=MN,
∴DM=EN,
∵DE⊥EF,∠EDM+∠DEM=90°,
∴∠DEF=90°,
∴∠DEM+∠FEN=90°,
∴∠EDM=∠FEN,
在△DME和△ENF中,
,
∴△DME≌△ENF(ASA),
∴EF=DE;
(2)解:由(1)知,△DME≌△ENF,
∴ME=NF,
∵四边形MNBC是矩形,
∴MC=BN,
又∵ME=MC,AB=4,AF=2,
∴BN=MC=NF=1,
∵∠EMC=90°,
∴CE=
,
∵AF∥CD,
∴△DGC∽△FGA,
∴
,
∴
,
∵AB=BC=4,∠B=90°,
∴AC=4
,
∵AC=AG+GC,
∴AG=
,CG=
,
∴GE=GC﹣CE=
=
.
22.
(1)∵AE⊥AD,∠BAC=90°,
∴∠EAD=∠CAB=90°,
∵∠B=30°,∠ADE=30°,
∴∠B=∠ADE,
∴△ADE∽△ABC;
(2)∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB=90°﹣∠CAD,
∵△ADE∽△ABC,
∴
,
∴
,
∵∠EAC=∠DAB,
∴△ACE∽△ABD;
(3)在Rt△ABC中,∠CAB=90°,AC=4,∠B=30°,
∴BC=2AC=8,AB=
=4
,
∵CE=x,CD=2CE,
∴CD=2x,
∵△ACE∽△ABD,
∴
,
∴
,
∴BD=
x,
∴BC=CD+BD=2x+
x=8,
解得:x=16﹣8
.
23.(1)∵四边形ABCO是矩形,
∴OA=BC=8,OC=AB=6,
在Rt△OCE中,CE=3,
∴OE=
,
∵AB∥OC,即AD∥OC,且AD=2,
∴
,
∴
,
∴PA=4,
∴PO=PA+OA=12,
∴在Rt△OPC中,OC=6,
∴CP=
,
∵OA∥BC,即OP∥CE,
∴
,
∴
,
∴EF=
OE=
,
CF=
CP=
,
∵(
)2+(
)2=
=9,
∴EF2+CF2=CE2
,
∴△CEF是直角三角形,
∴∠CFE=90°,
∴OE⊥CD;
(2)在Rt△CBD中,CB=8,BD=AB﹣AD=6﹣2=4,
根据勾股定理,得CD=
,
∵点G是CD的中点,
∴CG=DG=2
,
由(1)知:CP=6
,
∴DP=CP﹣CD=2
,
∴点G是CP的三等分点,
∵OA∥BC,即OP∥CH,
∴
,
∴
,
∴CH=6.
答:CH的长为6.
24.
(1)解:如图
所示:
与
相似,
理由:
;
,
,
与
相似;
(2)解:如图
所示:
即为所求;
(3)解:如图
所示:
和
即为所求.??
25.
(1)解:当
时,
,解得
,
.
∴
、
、
.
由题意得,设
对应的函数表达式为
,
又∵
经过点
,
∴
,
∴
.
∴
对应的函数表达式为
.
(2)解:∵
、
与
轴交点均为
、
,
∴
、
的对称轴都是直线
.
∴点
在直线
上.
∴
.
如图1,当A、C、P三点共线时,
的值最大,
此时点P为直线
与直线
的交点.
由
、
可求得,直线
对应的函数表达式为
.
∴点
.
(3)解:
由题意可得,
,
,
,
因为在
中,
,故
.
由
,得顶点
.
因为
的顶点P在直线
上,点Q在
上,
∴
不可能是直角.
第一种情况:当
时,
①如图2,当
时,则得
.
设
,则
,
∴
.
由
得
,解得
.
∵
时,点Q与点P重合,不符合题意,
∴舍去,此时
.
②如图3,当
时,则得
.
设
,则
.
∴
.
由
得
,解得
(舍),此时
.
第二种情况:当
时,
①如图4,当
时,则得
.
过Q作
交对称轴于点M,∴
.
∴
.由图2可知
,
∴
.
∴
,又
,代入得
.
∵点
,
∴点
.
②如图5,当
时,则
.
过Q作
交对称轴于点M,
∴
,则
.
由图3可知
,
,
∴
,
,
∴
.
又
,代入得
.
∵点
,
∴点
,
综上所述,
或
或
或
.
同课章节目录
