2020-2021学年浙教版九年级数学下册第三章《三视图与表面展开图》综合提高B卷(word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级数学下册第三章《三视图与表面展开图》综合提高B卷(word版 含答案) | 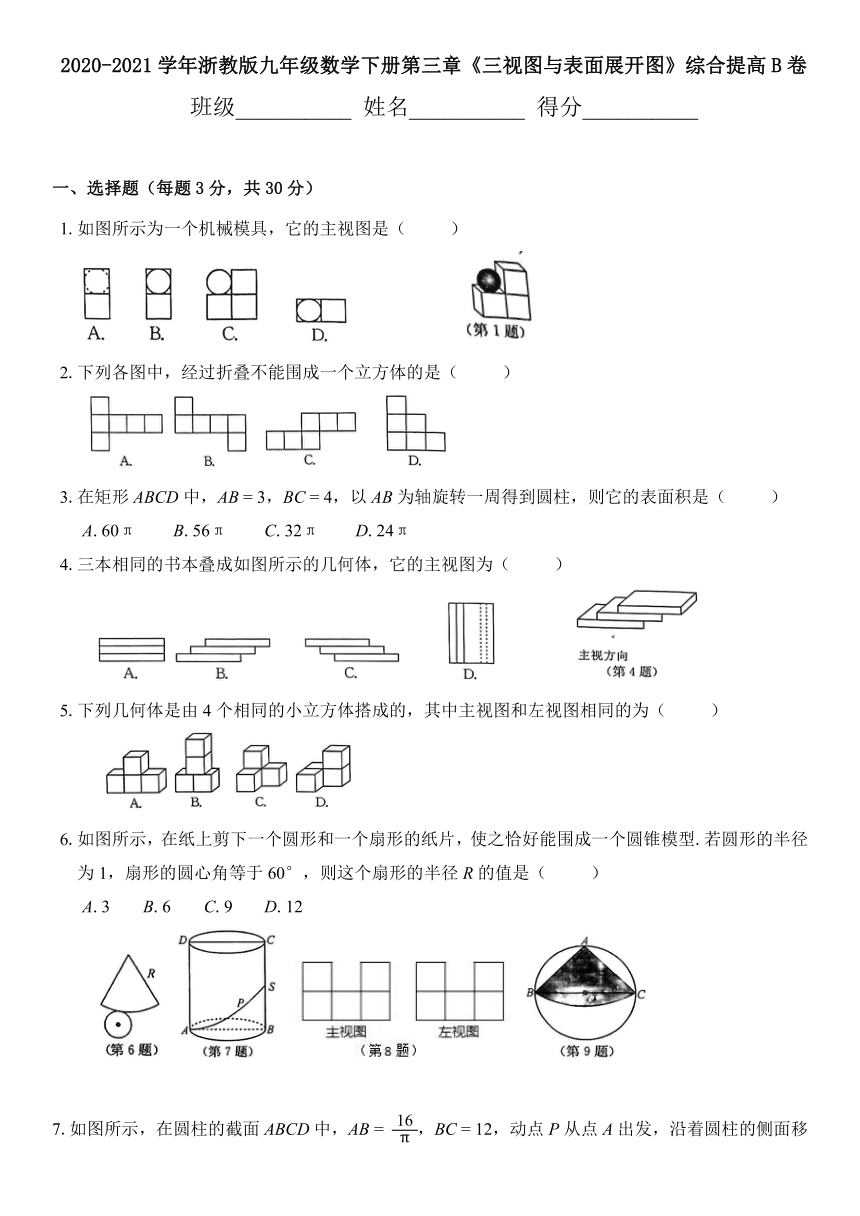 | |
| 格式 | zip | ||
| 文件大小 | 593.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 14:44:05 | ||
图片预览



文档简介
2020-2021学年浙教版九年级数学下册第三章《三视图与表面展开图》综合提高B卷班级__________
姓名__________
得分__________
一、选择题(每题3分,共30分)
1.如图所示为一个机械模具,它的主视图是(
)
2.下列各图中,经过折叠不能围成一个立方体的是(
)
3.在矩形ABCD中,AB
=
3,BC
=
4,以AB为轴旋转一周得到圆柱,则它的表面积是(
)
A.60π
B.56π
C.32π
D.24π
4.三本相同的书本叠成如图所示的几何体,它的主视图为(
)
5.下列几何体是由4个相同的小立方体搭成的,其中主视图和左视图相同的为(
)
6.如图所示,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆形的半径为1,扇形的圆心角等于60°,则这个扇形的半径R的值是(
)
A.3
B.6
C.9
D.12
7.如图所示,在圆柱的截面ABCD中,AB
=
,BC
=
12,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S的最短距离为(
)
A.10
B.12
C.20
D.14
8.一个几何体是由若干个相同的立方体组成的,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是(
)
A.15
B.13
C.11
D.5
9.如图所示,从一块直径为24
cm的圆形纸片上剪出一个圆心角为90°的扇形BAC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.12
cm
B.6
cm
C.3
cm
D.2
cm
10.如图所示,用邻边长分别为a,b(a
<
b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.若把半圆作为圆锥形生日帽的侧面,小圆恰好能作为底面,从而做成两个生日帽(拼接处材料忽略不计),则a与b满足的关系是(
)
A.b
=
a
B.b
=
C.b
=
D.b
=
a
二、填空题(每题4分,共24分)
12.如图所示为一个立方体纸盒的展开图,要在其中的三个正方形A,B,C内分别填入适当的数,使它们折成立方体后相对的面上的两个数互为相反数,则A
=
_________
,B
=
_________
.
13.如图所示,圆锥的高为2
cm,∠
=
30°,则圆锥的侧面积为
_________
cm2.
(第13题)
(第14题)
(第15题)
(第16题)
14.已知三棱柱的三视图如图所示,在△EFG中,EF
=
4
cm,EG
=
6
cm,∠EGF
=
30°,则AB的长为
_________
cm.
15.一个几何体的主视图和俯视图如图所示,若这个几何体最多由m个小正方体组成,最少由n个小正方体组成,则m
+
n
=
_________
.
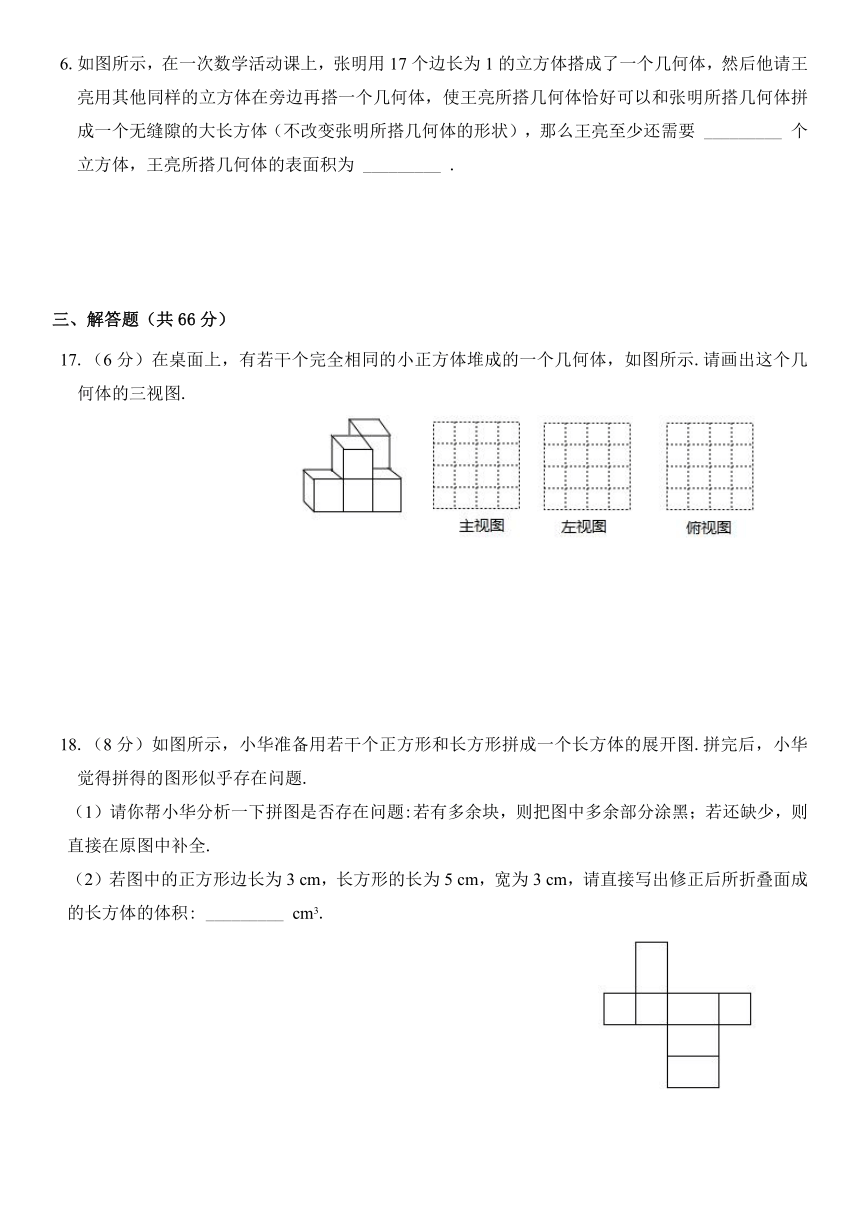
6.如图所示,在一次数学活动课上,张明用17个边长为1的立方体搭成了一个几何体,然后他请王亮用其他同样的立方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
_________
个立方体,王亮所搭几何体的表面积为
_________
.
三、解答题(共66分)
17.(6分)在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.请画出这个几何体的三视图.
18.(8分)如图所示,小华准备用若干个正方形和长方形拼成一个长方体的展开图.拼完后,小华觉得拼得的图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为3
cm,长方形的长为5
cm,宽为3
cm,请直接写出修正后所折叠面成的长方体的体积:
_________
cm3.
19.(8分)将一直径为17
cm的圆形纸片(如图1所示)剪成如图2所示形状的纸片,再将纸片沿虚线折叠得到立方体(如图3所示)形状的纸盒,则纸盒的体积最大可以为多少?
20.(10分)已知一圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)的函数表达式.
(2)写出自变量r的取值范围.
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
21.(10分)已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)若制作这个模型的木料密度为360
kg/m3,则这个模型的质量是多少千克?
(3)若油漆这个模型,每千克油漆可以漆4
m2,则油漆整个模型需要油漆多少千克?
主视图
左视图
俯视图
22.(12分)新年晚会会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图所示.
(1)数出每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:(2)观察表中数据,猜想多面体的顶点数(V)、棱数(E)和面数(F)之间的关系.
(3)数学家队拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V
=
196,棱的条数E
=
294,请你用欧拉公式求这个多面体的面数.
23.(12分)为了培养学生的动手能力,某中学安排各班学生制作生日帽.如果生日帽(圆锥形状)的规格是母线长42
cm,底面直径为16
cm.
(1)求生日帽的侧面展开图(扇形)的圆心角的度数.(结果精确到度)
(2)已知A种规格的纸片能做3个生日帽,B种规格的纸片能做4个生日帽,该校有26个班级,每班需制作一顶生日帽,写出所有A种规格的纸片张数y关于B种规格的纸片张数x的函数表达式及x的最大值与最小值.学校应购买A,B两种规格的纸片各多少张才不会造成浪费?
(3)现有一张边长为79
cm的正方形纸片,它最多能制作几个这种规格的生日帽(生日帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出生日帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
答
案
姓名__________
得分__________
一、选择题(每题3分,共30分)
1.如图所示为一个机械模具,它的主视图是(
)
2.下列各图中,经过折叠不能围成一个立方体的是(
)
3.在矩形ABCD中,AB
=
3,BC
=
4,以AB为轴旋转一周得到圆柱,则它的表面积是(
)
A.60π
B.56π
C.32π
D.24π
4.三本相同的书本叠成如图所示的几何体,它的主视图为(
)
5.下列几何体是由4个相同的小立方体搭成的,其中主视图和左视图相同的为(
)
6.如图所示,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆形的半径为1,扇形的圆心角等于60°,则这个扇形的半径R的值是(
)
A.3
B.6
C.9
D.12
7.如图所示,在圆柱的截面ABCD中,AB
=
,BC
=
12,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S的最短距离为(
)
A.10
B.12
C.20
D.14
8.一个几何体是由若干个相同的立方体组成的,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是(
)
A.15
B.13
C.11
D.5
9.如图所示,从一块直径为24
cm的圆形纸片上剪出一个圆心角为90°的扇形BAC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.12
cm
B.6
cm
C.3
cm
D.2
cm
10.如图所示,用邻边长分别为a,b(a
<
b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.若把半圆作为圆锥形生日帽的侧面,小圆恰好能作为底面,从而做成两个生日帽(拼接处材料忽略不计),则a与b满足的关系是(
)
A.b
=
a
B.b
=
C.b
=
D.b
=
a
二、填空题(每题4分,共24分)
12.如图所示为一个立方体纸盒的展开图,要在其中的三个正方形A,B,C内分别填入适当的数,使它们折成立方体后相对的面上的两个数互为相反数,则A
=
_________
,B
=
_________
.
13.如图所示,圆锥的高为2
cm,∠
=
30°,则圆锥的侧面积为
_________
cm2.
(第13题)
(第14题)
(第15题)
(第16题)
14.已知三棱柱的三视图如图所示,在△EFG中,EF
=
4
cm,EG
=
6
cm,∠EGF
=
30°,则AB的长为
_________
cm.
15.一个几何体的主视图和俯视图如图所示,若这个几何体最多由m个小正方体组成,最少由n个小正方体组成,则m
+
n
=
_________
.
6.如图所示,在一次数学活动课上,张明用17个边长为1的立方体搭成了一个几何体,然后他请王亮用其他同样的立方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要
_________
个立方体,王亮所搭几何体的表面积为
_________
.
三、解答题(共66分)
17.(6分)在桌面上,有若干个完全相同的小正方体堆成的一个几何体,如图所示.请画出这个几何体的三视图.
18.(8分)如图所示,小华准备用若干个正方形和长方形拼成一个长方体的展开图.拼完后,小华觉得拼得的图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为3
cm,长方形的长为5
cm,宽为3
cm,请直接写出修正后所折叠面成的长方体的体积:
_________
cm3.
19.(8分)将一直径为17
cm的圆形纸片(如图1所示)剪成如图2所示形状的纸片,再将纸片沿虚线折叠得到立方体(如图3所示)形状的纸盒,则纸盒的体积最大可以为多少?
20.(10分)已知一圆锥的侧面积为16πcm2.
(1)求圆锥的母线长L(cm)关于底面半径r(cm)的函数表达式.
(2)写出自变量r的取值范围.
(3)当圆锥的侧面展开图是圆心角为90°的扇形时,求圆锥的高.
21.(10分)已知一个模型的三视图如图所示(单位:m).
(1)请描述这个模型的形状.
(2)若制作这个模型的木料密度为360
kg/m3,则这个模型的质量是多少千克?
(3)若油漆这个模型,每千克油漆可以漆4
m2,则油漆整个模型需要油漆多少千克?
主视图
左视图
俯视图
22.(12分)新年晚会会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图所示.
(1)数出每一个多面体具有的顶点数(V)、棱数(E)和面数(F),并且把结果记入表中:(2)观察表中数据,猜想多面体的顶点数(V)、棱数(E)和面数(F)之间的关系.
(3)数学家队拉证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数V
=
196,棱的条数E
=
294,请你用欧拉公式求这个多面体的面数.
23.(12分)为了培养学生的动手能力,某中学安排各班学生制作生日帽.如果生日帽(圆锥形状)的规格是母线长42
cm,底面直径为16
cm.
(1)求生日帽的侧面展开图(扇形)的圆心角的度数.(结果精确到度)
(2)已知A种规格的纸片能做3个生日帽,B种规格的纸片能做4个生日帽,该校有26个班级,每班需制作一顶生日帽,写出所有A种规格的纸片张数y关于B种规格的纸片张数x的函数表达式及x的最大值与最小值.学校应购买A,B两种规格的纸片各多少张才不会造成浪费?
(3)现有一张边长为79
cm的正方形纸片,它最多能制作几个这种规格的生日帽(生日帽的粘接处忽略不计).请在比例尺为1:15的正方形纸片上画出生日帽的侧面展开图的裁剪草图,并利用所学的数学知识说明其可行性.
答
案
