4.4相似三角形的性质及其应用(1)
图片预览


文档简介
(共22张PPT)
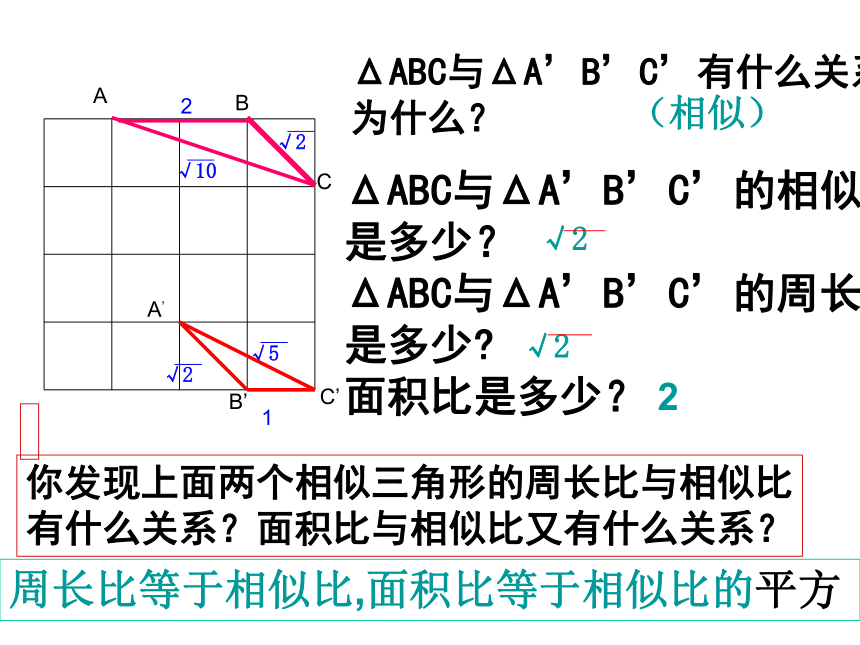
ΔABC与ΔA’B’C’的相似比
是多少?
ΔABC与ΔA’B’C’的周长比
是多少
面积比是多少?
ΔABC与ΔA’B’C’有什么关系? 为什么?
你发现上面两个相似三角形的周长比与相似比
有什么关系?面积比与相似比又有什么关系?
(相似)
√2
2
√2
√10
2
√2
1
√5
√2
A
B
C
A’
C’
B’
周长比等于相似比,面积比等于相似比的平方
A
B
C
A’
B’
C’
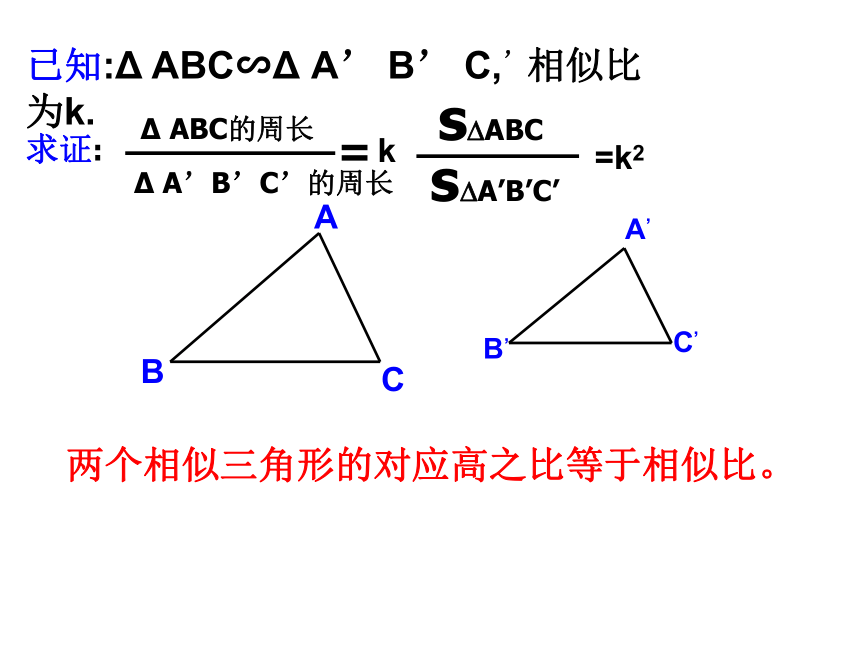
已知:Δ ABC∽Δ A’ B’ C,’相似比为k.
=k2
k
两个相似三角形的对应高之比等于相似比。
求证:
Δ ABC的周长
Δ A’B’C’的周长
=
s ABC
s A’B’C’
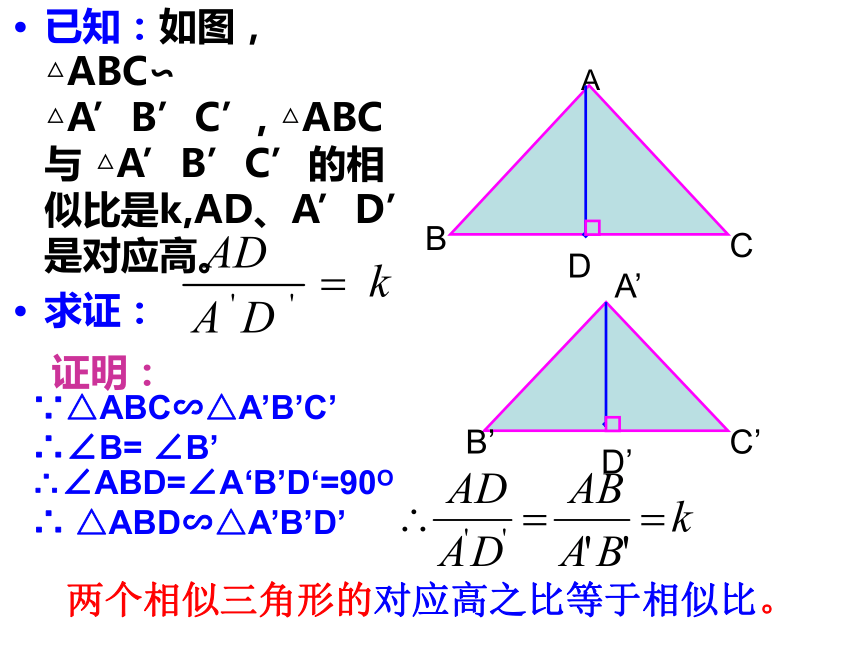
已知:如图,△ABC∽ △A’B’C’, △ABC与 △A’B’C’的相似比是k,AD、A’D’是对应高。
求证:
A
B
C
B’
A’
C’
D
D’
证明:
∵△ABC∽△A’B’C’
∴∠B= ∠B’
∴∠ABD=∠A‘B’D‘=90O
∴ △ABD∽△A’B’D’
两个相似三角形的对应高之比等于相似比。
A
B
C
A’
B’
C’
∵Δ ABC∽Δ A’ B’ C,’相似比为k.
=k2
s ABC
s A’B’C’
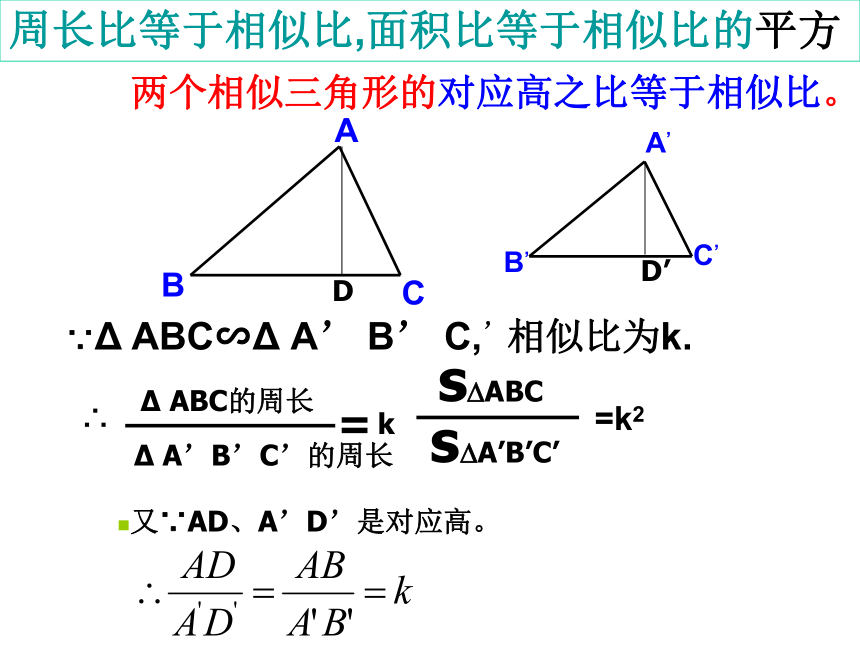
周长比等于相似比,面积比等于相似比的平方
两个相似三角形的对应高之比等于相似比。
Δ ABC的周长
Δ A’B’C’的周长
=
k
∴
又∵AD、A’D’是对应高。
D
D’
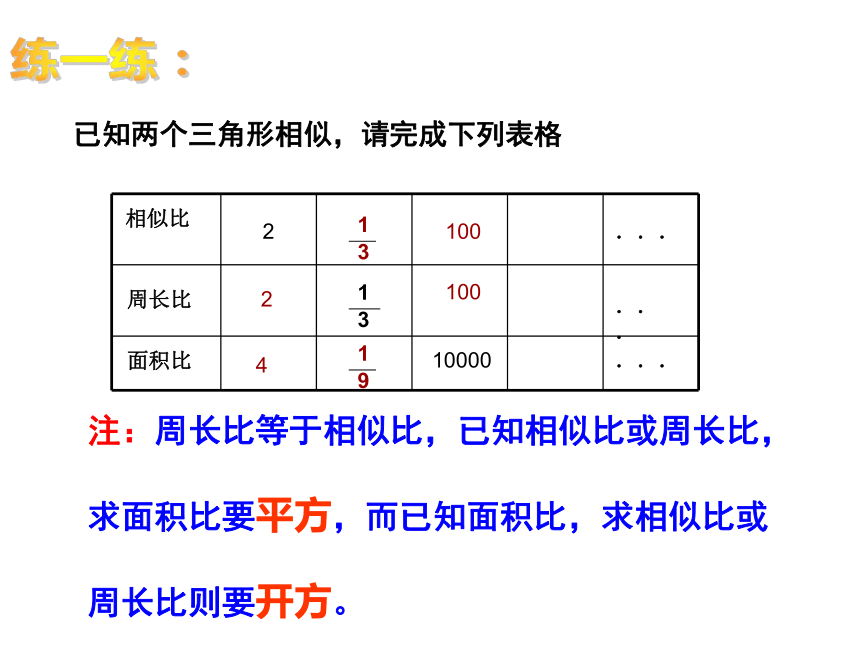
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方,而已知面积比,求相似比或
周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
1.在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍
答:三角形的边长,周长放大为10倍.
三角形的面积放大为100倍.
三角形的角大小不变.
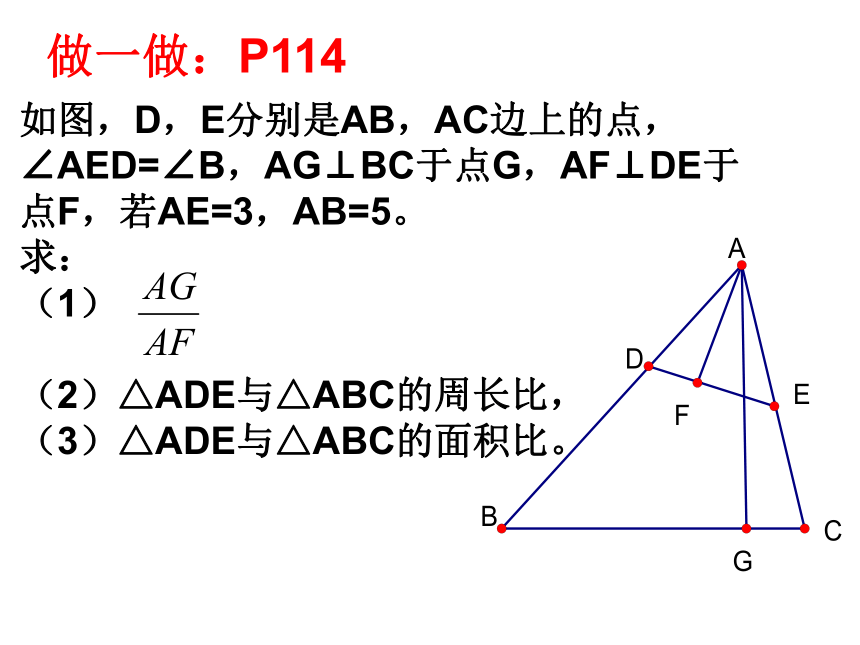
做一做:P114
如图,D,E分别是AB,AC边上的点,∠AED=∠B,AG⊥BC于点G,AF⊥DE于点F,若AE=3,AB=5。 求:
(1)
(2)△ADE与△ABC的周长比, (3)△ADE与△ABC的面积比。
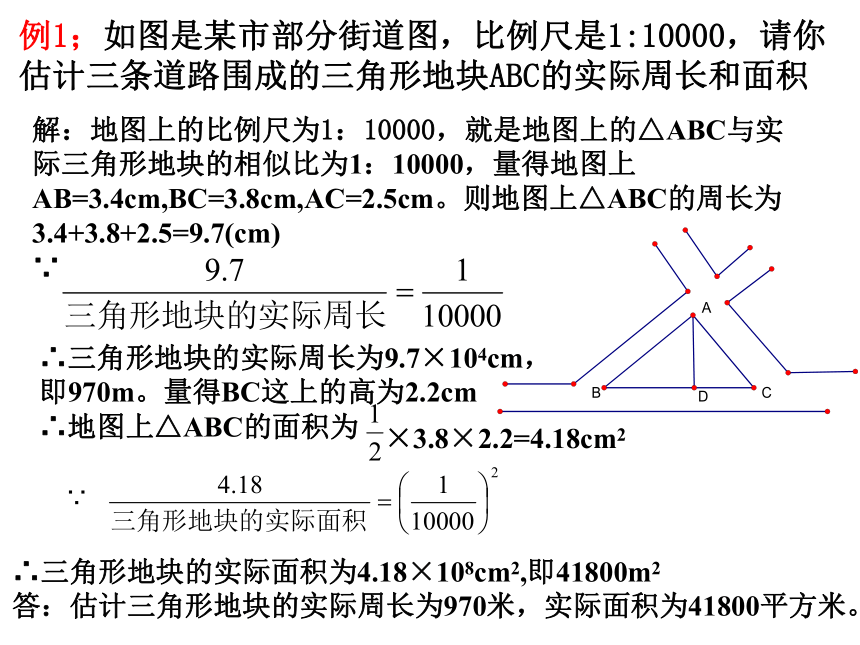
例1;如图是某市部分街道图,比例尺是1:10000,请你估计三条道路围成的三角形地块ABC的实际周长和面积
解:地图上的比例尺为1:10000,就是地图上的△ABC与实际三角形地块的相似比为1:10000,量得地图上AB=3.4cm,BC=3.8cm,AC=2.5cm。则地图上△ABC的周长为3.4+3.8+2.5=9.7(cm)
∵
∴三角形地块的实际周长为9.7×104cm,
即970m。量得BC这上的高为2.2cm
∴地图上△ABC的面积为
×3.8×2.2=4.18cm2
∴三角形地块的实际面积为4.18×108cm2,即41800m2
答:估计三角形地块的实际周长为970米,实际面积为41800平方米。
∵
2、在△ABC中,DE BC,E、D分别在AC、AB上,EC=2AE,则S △ ADE:S四边形DBCE的比为______
练习
3、如图, △ABC中,DE FG BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
4.已知:梯形ABCD中,AD∥BC,AD=36,BC=60cm,延长两腰BD,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
A
B
C
D
E
F
O
练习
5、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽ Δ______.它们的相似比K =_______,
A
B
C
E
D
G
如图,在△ABC中,∠C=Rt∠,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现在有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P做PE∥BC交AD于点E,连接EQ。设动点运动的时间为x.
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B和D)上移动时,设△EDQ的面积为y,求y与t的函数关系式,并写出自变量x的取值范围;
(3)当x为何值时,△EDQ为直角三角形
D
E
Q
B
C
P
A
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:被削去的部分面积有多大?它的周长是多少?
D
E
30m
18m
B
C
A
B
A
C
D
E
解:如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积
30m
18m
A
D
E
1.过E作EF//AB交BC于F,其他条件不变,则
ΔEFC的面积等于多少?BDEF面积为多少?
2.若设sΔABC=S, SΔADE=S1, SΔEFC=S2.
请猜想:S与S1、S2之间存在怎样的关系?
你能加以验证吗?
√ S = √S1+ √S2
B
C
F
48m2
36m2
证明:DE//BC
>
ΔADE∽ΔABC
>
S1
S
=(
A C
A E
)
2
EF//AB
>
ΔEFC∽ΔABC
>
S2
S
=
A C
C E
(
)
2
√S
>
√S1
=
A C
A E
√S
>
√S2
A C
C E
=
}
>
√S
√S
√S2
√S1
+
=1
√S1
>
√S2
+
√S
=
16
36
30m
18m
ΔABC的面积为100m2,
A
C
B
P
F
M
N
G
E
D
S3
S1
S2
如图,DE//BC,FG//AB,MN//AC,
且DE、FG、MN交于点P。
若记SΔDPM= S1, SΔPEF= S2, SΔGNP= S3
SΔABC= S、S与S1、 S2、S3之间是否也有
类似结论?猜想并加以验证。
探究
1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.通过本节课的学习,你有没有新的想法或发现?
你觉得还有什么问题需要继续讨论吗?
相似三角形对应中线的比与对应
角平分线的比等于相似比。
你能类比证明吗
A
B
C
A’
B’
C’
D
D’
3、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽ Δ______.它们的相似比K =_______,
A
B
C
E
D
G
1.作业本
2. 探究的推理过程课外整理完成,
各组自行组织讨论交流
ΔABC与ΔA’B’C’的相似比
是多少?
ΔABC与ΔA’B’C’的周长比
是多少
面积比是多少?
ΔABC与ΔA’B’C’有什么关系? 为什么?
你发现上面两个相似三角形的周长比与相似比
有什么关系?面积比与相似比又有什么关系?
(相似)
√2
2
√2
√10
2
√2
1
√5
√2
A
B
C
A’
C’
B’
周长比等于相似比,面积比等于相似比的平方
A
B
C
A’
B’
C’
已知:Δ ABC∽Δ A’ B’ C,’相似比为k.
=k2
k
两个相似三角形的对应高之比等于相似比。
求证:
Δ ABC的周长
Δ A’B’C’的周长
=
s ABC
s A’B’C’
已知:如图,△ABC∽ △A’B’C’, △ABC与 △A’B’C’的相似比是k,AD、A’D’是对应高。
求证:
A
B
C
B’
A’
C’
D
D’
证明:
∵△ABC∽△A’B’C’
∴∠B= ∠B’
∴∠ABD=∠A‘B’D‘=90O
∴ △ABD∽△A’B’D’
两个相似三角形的对应高之比等于相似比。
A
B
C
A’
B’
C’
∵Δ ABC∽Δ A’ B’ C,’相似比为k.
=k2
s ABC
s A’B’C’
周长比等于相似比,面积比等于相似比的平方
两个相似三角形的对应高之比等于相似比。
Δ ABC的周长
Δ A’B’C’的周长
=
k
∴
又∵AD、A’D’是对应高。
D
D’
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方,而已知面积比,求相似比或
周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
1.在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍
答:三角形的边长,周长放大为10倍.
三角形的面积放大为100倍.
三角形的角大小不变.
做一做:P114
如图,D,E分别是AB,AC边上的点,∠AED=∠B,AG⊥BC于点G,AF⊥DE于点F,若AE=3,AB=5。 求:
(1)
(2)△ADE与△ABC的周长比, (3)△ADE与△ABC的面积比。
例1;如图是某市部分街道图,比例尺是1:10000,请你估计三条道路围成的三角形地块ABC的实际周长和面积
解:地图上的比例尺为1:10000,就是地图上的△ABC与实际三角形地块的相似比为1:10000,量得地图上AB=3.4cm,BC=3.8cm,AC=2.5cm。则地图上△ABC的周长为3.4+3.8+2.5=9.7(cm)
∵
∴三角形地块的实际周长为9.7×104cm,
即970m。量得BC这上的高为2.2cm
∴地图上△ABC的面积为
×3.8×2.2=4.18cm2
∴三角形地块的实际面积为4.18×108cm2,即41800m2
答:估计三角形地块的实际周长为970米,实际面积为41800平方米。
∵
2、在△ABC中,DE BC,E、D分别在AC、AB上,EC=2AE,则S △ ADE:S四边形DBCE的比为______
练习
3、如图, △ABC中,DE FG BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
4.已知:梯形ABCD中,AD∥BC,AD=36,BC=60cm,延长两腰BD,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
A
B
C
D
E
F
O
练习
5、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽ Δ______.它们的相似比K =_______,
A
B
C
E
D
G
如图,在△ABC中,∠C=Rt∠,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现在有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P做PE∥BC交AD于点E,连接EQ。设动点运动的时间为x.
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B和D)上移动时,设△EDQ的面积为y,求y与t的函数关系式,并写出自变量x的取值范围;
(3)当x为何值时,△EDQ为直角三角形
D
E
Q
B
C
P
A
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:被削去的部分面积有多大?它的周长是多少?
D
E
30m
18m
B
C
A
B
A
C
D
E
解:如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积
30m
18m
A
D
E
1.过E作EF//AB交BC于F,其他条件不变,则
ΔEFC的面积等于多少?BDEF面积为多少?
2.若设sΔABC=S, SΔADE=S1, SΔEFC=S2.
请猜想:S与S1、S2之间存在怎样的关系?
你能加以验证吗?
√ S = √S1+ √S2
B
C
F
48m2
36m2
证明:DE//BC
>
ΔADE∽ΔABC
>
S1
S
=(
A C
A E
)
2
EF//AB
>
ΔEFC∽ΔABC
>
S2
S
=
A C
C E
(
)
2
√S
>
√S1
=
A C
A E
√S
>
√S2
A C
C E
=
}
>
√S
√S
√S2
√S1
+
=1
√S1
>
√S2
+
√S
=
16
36
30m
18m
ΔABC的面积为100m2,
A
C
B
P
F
M
N
G
E
D
S3
S1
S2
如图,DE//BC,FG//AB,MN//AC,
且DE、FG、MN交于点P。
若记SΔDPM= S1, SΔPEF= S2, SΔGNP= S3
SΔABC= S、S与S1、 S2、S3之间是否也有
类似结论?猜想并加以验证。
探究
1.这节课我们学到了哪些知识?
2.我们是用哪些方法获得这些知识的?
3.通过本节课的学习,你有没有新的想法或发现?
你觉得还有什么问题需要继续讨论吗?
相似三角形对应中线的比与对应
角平分线的比等于相似比。
你能类比证明吗
A
B
C
A’
B’
C’
D
D’
3、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACD∽ Δ______.它们的相似比K =_______,
A
B
C
E
D
G
1.作业本
2. 探究的推理过程课外整理完成,
各组自行组织讨论交流
同课章节目录
